第24章 圆 综合测试题(含详解) 2024—2025学年人教版数学九年级上册
文档属性
| 名称 | 第24章 圆 综合测试题(含详解) 2024—2025学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 341.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 00:00:00 | ||
图片预览


文档简介
第24章 圆综合测试题
考试范围:24章 圆;考试时间:100分钟;总分:120
学校:___________姓名:___________班级:___________考号:___________
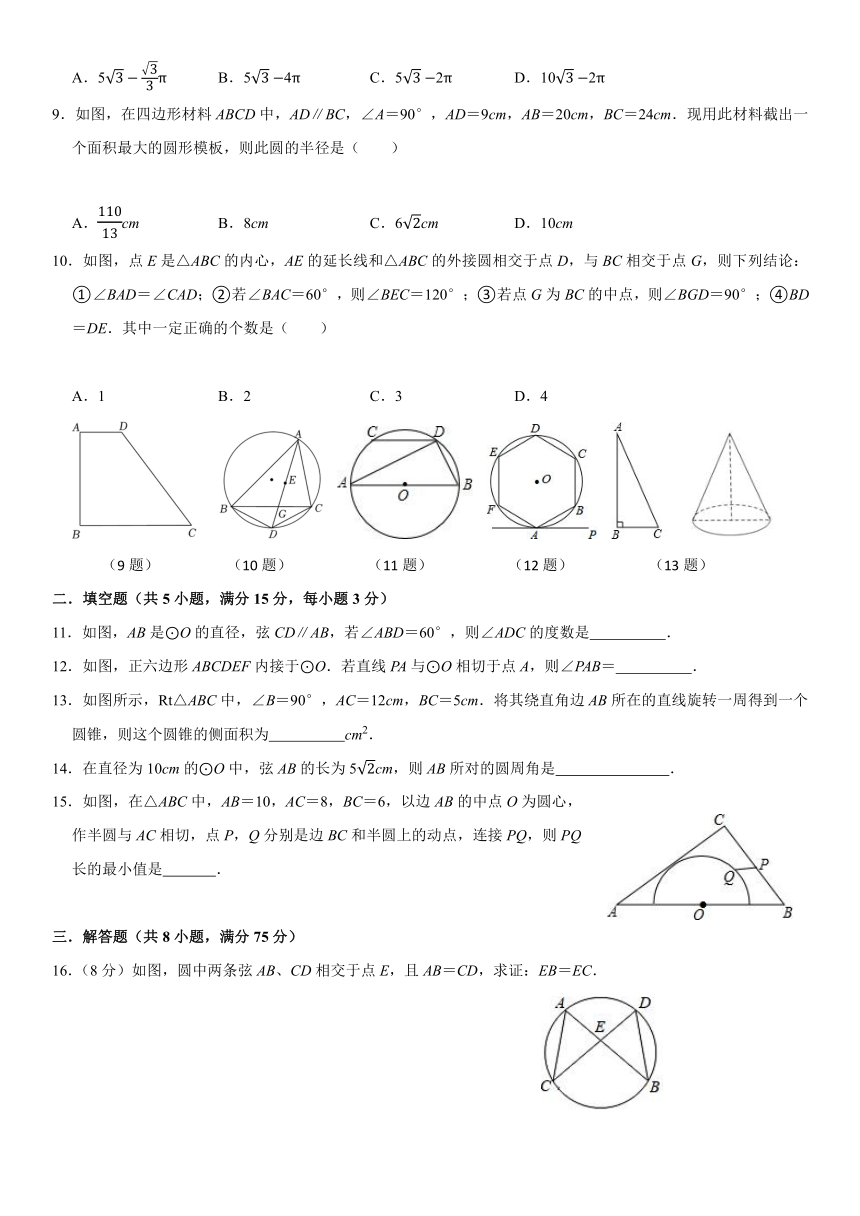
一.选择题(共10小题,满分30分,每小题3分)
1.下列说法:
①直径是弦;②半圆是弧;③半径相等的两个圆是等圆;④长度相等的两条弧是等弧;
⑤在同圆中任意两条直径都互相平分.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
2.已知⊙O的半径为3cm,点A到圆心O的距离为4cm,则点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
3.如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
A.22° B.26° C.32° D.68°
4.如图,A是⊙O上一点,BC是直径,AC=2,AB=4,点D在⊙O上且平分,则DC的
长为( )
A. B. C. D.
(3题) (4题) (5题) (6题) (7题)
5.如图,圆O与正方形ABCD的两边AB、AD相切,且DE与圆O相切于E点.若圆O的半径为5,且AB=11,则DE的长度为何?( )
A.5 B.6 C. D.
6.如图,已知BC与⊙O相切于点B,CO的延长线交⊙O于点A,连接AB,若BC=2,AC=6,则⊙O的半径为( )
A.1.5 B.2 C.2.5 D.3
7.如图,在5×6的正方形网格中,若将△ABC绕着点A逆时针旋转得到△AB′C′,则的长为( )
A.π B. C.7π D.6π
8.如图,在△ABC中,∠ABC=90°,∠ACB=30°,AB=4,点O为BC的中点,以O为圆心,OB长为半径作半圆,交AC于点D,则图中阴影部分的面积是( )
A.5π B.54π C.52π D.102π
9.如图,在四边形材料ABCD中,AD∥BC,∠A=90°,AD=9cm,AB=20cm,BC=24cm.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
A.cm B.8cm C.6cm D.10cm
10.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,与BC相交于点G,则下列结论:①∠BAD=∠CAD;②若∠BAC=60°,则∠BEC=120°;③若点G为BC的中点,则∠BGD=90°;④BD=DE.其中一定正确的个数是( )
A.1 B.2 C.3 D.4
(9题) (10题) (11题) (12题) (13题)
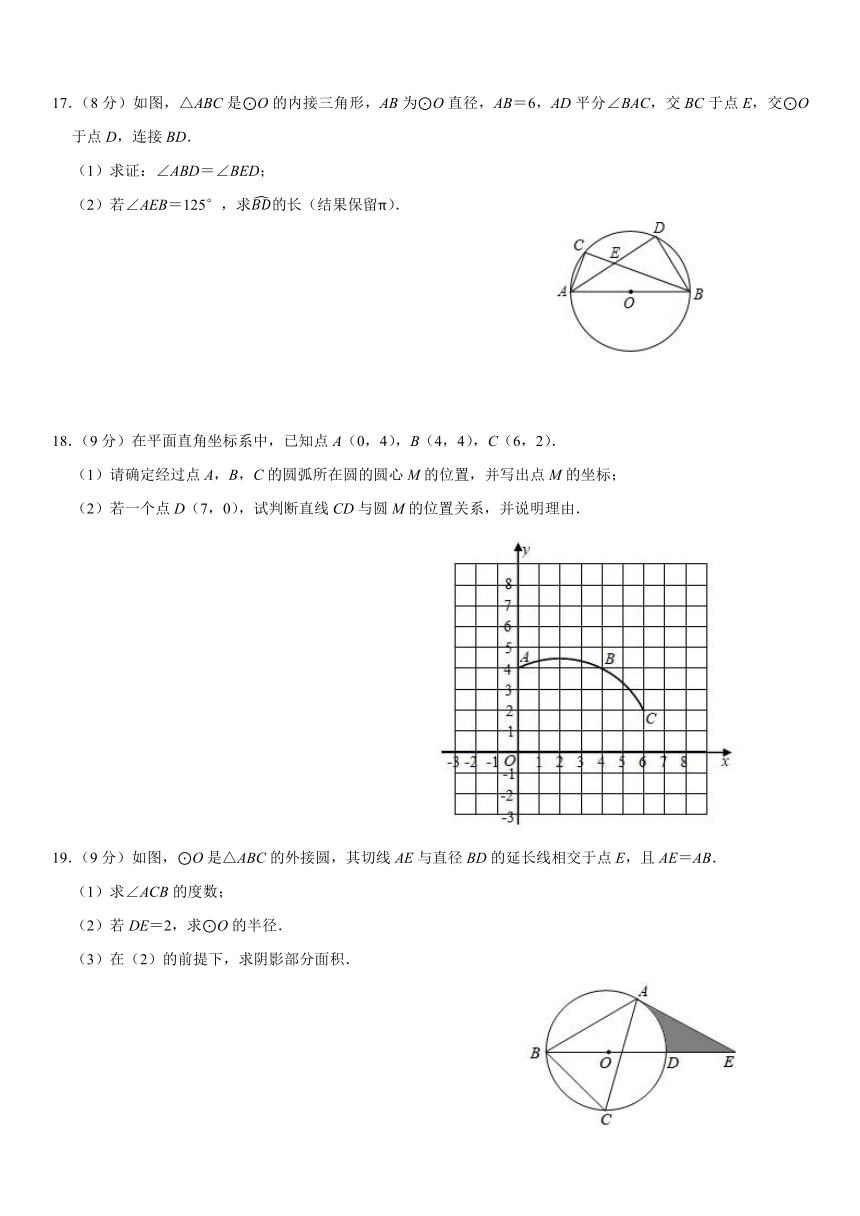
二.填空题(共5小题,满分15分,每小题3分)
11.如图,AB是⊙O的直径,弦CD∥AB,若∠ABD=60°,则∠ADC的度数是 .
12.如图,正六边形ABCDEF内接于⊙O.若直线PA与⊙O相切于点A,则∠PAB= .
13.如图所示,Rt△ABC中,∠B=90°,AC=12cm,BC=5cm.将其绕直角边AB所在的直线旋转一周得到一个圆锥,则这个圆锥的侧面积为 cm2.
14.在直径为10cm的⊙O中,弦AB的长为5cm,则AB所对的圆周角是 .
15.如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是 .
三.解答题(共8小题,满分75分)
16.(8分)如图,圆中两条弦AB、CD相交于点E,且AB=CD,求证:EB=EC.
17.(8分)如图,△ABC是⊙O的内接三角形,AB为⊙O直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连接BD.
(1)求证:∠ABD=∠BED;
(2)若∠AEB=125°,求的长(结果保留π).
18.(9分)在平面直角坐标系中,已知点A(0,4),B(4,4),C(6,2).
(1)请确定经过点A,B,C的圆弧所在圆的圆心M的位置,并写出点M的坐标;
(2)若一个点D(7,0),试判断直线CD与圆M的位置关系,并说明理由.
19.(9分)如图,⊙O是△ABC的外接圆,其切线AE与直径BD的延长线相交于点E,且AE=AB.
(1)求∠ACB的度数;
(2)若DE=2,求⊙O的半径.
(3)在(2)的前提下,求阴影部分面积.
20.(9分)如图,AB是⊙O的直径,弦AC=6,BC=8,∠ACB的平分线交⊙O于点D,连接AD.
(1)求直径AB的长;
(2)求阴影部分的面积.(结果保留π)
21.(9分)如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为点E,过点C作DA的平行线与AF相交于点F,CD=4,BE=2.
(1)求AD的长;
(2)求证:四边形FADC是菱形;
(3)求证:FC是⊙O的切线.
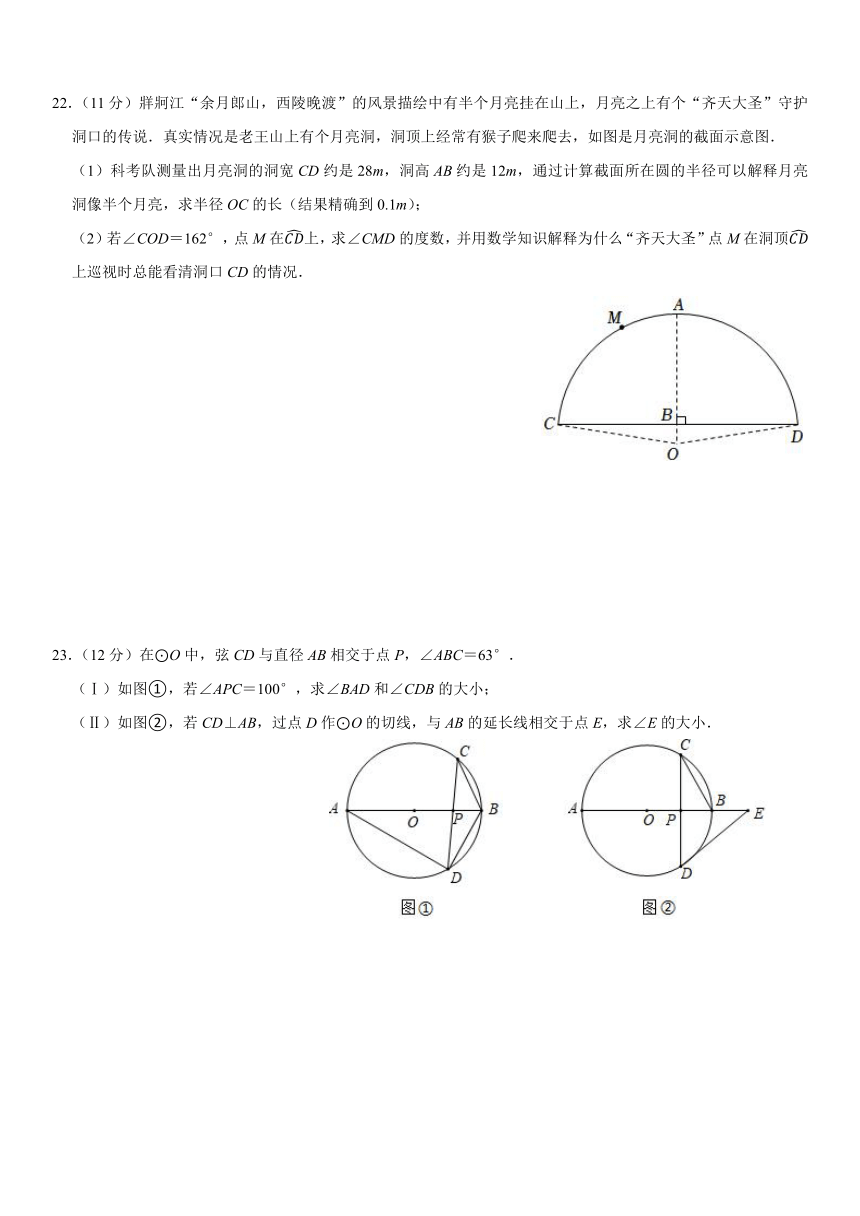
22.(11分)牂牁江“余月郎山,西陵晚渡”的风景描绘中有半个月亮挂在山上,月亮之上有个“齐天大圣”守护洞口的传说.真实情况是老王山上有个月亮洞,洞顶上经常有猴子爬来爬去,如图是月亮洞的截面示意图.
(1)科考队测量出月亮洞的洞宽CD约是28m,洞高AB约是12m,通过计算截面所在圆的半径可以解释月亮洞像半个月亮,求半径OC的长(结果精确到0.1m);
(2)若∠COD=162°,点M在上,求∠CMD的度数,并用数学知识解释为什么“齐天大圣”点M在洞顶上巡视时总能看清洞口CD的情况.
23.(12分)在⊙O中,弦CD与直径AB相交于点P,∠ABC=63°.
(Ⅰ)如图①,若∠APC=100°,求∠BAD和∠CDB的大小;
(Ⅱ)如图②,若CD⊥AB,过点D作⊙O的切线,与AB的延长线相交于点E,求∠E的大小.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:①直径是弦,正确,符合题意;
②半圆是弧,正确,符合题意;
③半径相等的两个圆是等圆,正确,符合题意;
④长度相等的两条弧不一定是等弧,原命题错误,不符合题意;
⑤在同圆中任意两条直径都互相平分,正确,符合题意,
正确的有4个,
选:D.
2.解:OA>3cm,则点A与⊙O的位置关系是:点A在圆外.
选:C.
3.解:∵∠A与∠BOC是同弧所对的圆周角与圆心角,∠A=68°,
∴∠BOC=2∠A=136°.
∵OB=OC,
∴∠OBC22°.
选:A.
4.解:∵A是⊙O上一点,BC是直径,
∴∠BAC=∠BDC=90°,
在Rt△ABC中,AC=2,AB=4,
由勾股定理得:AB2+AC2=BC2,即BC2=22+42=20,
∵点D在⊙O上且平分弧BC,
∴BD=DC,
在Rt△BDC中,由勾股定理得:BD2+DC2=BC2,即2DC2=BC2=20,
解得:DC,
选:B.
5.解:
连接OM、ON,
∵四边形ABCD是正方形,
∴AD=AB=11,∠A=90°,
∵圆O与正方形ABCD的两边AB、AD相切,
∴∠OMA=∠ONA=90°=∠A,
∵OM=ON,
∴四边形ANOM是正方形,
∴AM=OM=5,
∵AD和DE与圆O相切,圆O的半径为5,
∴AM=5,DM=DE,
∴DE=11﹣5=6,
选:B.
6.解:连接OB,
∵BC与⊙O相切于点B,
∴OB⊥BC,
设⊙O的半径为r,
在Rt△OBC中,OB2+BC2=OC2,
即,
解得:r=2,
选:B.
7.解:根据图示知,∠BAB′=45°,
∴的长为:π.
选:A.
8.解:连接OD.
在△ABC中,∠ABC=90°,∠ACB=30°,AB=4,
∴BCAB=4,
∴OC=OD=OB=2,
∴∠DOB=2∠C=60°,
∴S阴=S△ACB﹣S△COD﹣S扇形ODB4×4
=832π
=52π.
选:C.
9.解:如图,当AB,BC,CD相切于⊙O于点E,F,G时,⊙O的面积最大.连接OA,OB,OC,OD,OE,OF,OG,过点D作DH⊥BC于点H.
∵AD∥CB,∠BAD=90°,
∴∠ABC=90°,
∵∠DHB=90°,
∴四边形ABHD是矩形,
∴AB=DH=20cm,AD=BH=9cm,
∵BC=24cm,
∴CH=BC﹣BH=24﹣9=15(cm),
∴CD25(cm),
设OE=OF=OG=r cm,
则有(9+24)×2020×r24×r25×r9×(20﹣r),
∴r=8,
选:B.
10.解:∵E是△ABC的内心,
∴AD平分∠BAC,
∴∠BAD=∠CAD,①正确;
如图,连接BE,CE,
∵E是△ABC的内心,
∴∠EBC∠ABC,∠ECBACB,
∵∠BAC=60°,
∴∠ABC+∠ACB=120°,
∴∠BEC=180°﹣∠EBC﹣∠ECB=180°(∠ABC+∠ACB)=120°,②正确;
∵∠BAD=∠CAD,
∴,
∴OD⊥BC,
∵点G为BC的中点,
∴G一定在OD上,
∴∠BGD=90°,③正确;
如图,连接BE,
∴BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠DBC=∠DAC=∠BAD,
∴∠DBC+∠EBC=∠EBA+∠EAB,
∴∠DBE=∠DEB,
∴DB=DE,④正确.
∴一定正确的①②③④,共4个.
选:D.
二.填空题(共5小题,满分15分,每小题3分)
11.解:∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角);
又∵∠ABD=60°,
∴∠DAB=30°(直角三角形的两个锐角互余);
又∵CD∥AB,
∴∠ADC=∠DAB(两直线平行,内错角相等),
∴∠ADC=30°(等量代换).
答案为:30°.
12.解:连接OB,AD,BD,
∵多边形ABCDEF是正多边形,
∴AD为外接圆的直径,
∠AOB60°,
∴∠ADB∠AOB60°=30°.
∵直线PA与⊙O相切于点A,
∴∠PAB=∠ADB=30°.
答案为:30°.
13.解:圆锥的侧面积=π×5×12=60πcm2.
14.解:连接OA、OB,∠C和∠D为AB所对的圆周角,如图,
∵OA=OB=5,AB=5,
∴OA2+OB2=AB2,
∴△OAB为直角三角形,
∴∠AOB=90°,
∴∠C∠AOB=45°,
∴∠D=180°∠C=135°.
即AB所对的圆周角为45°或135°.
答案为45°或135°.
15.解:
当O、Q、P三点一线且OP⊥BC时,PQ有最小值,设AC与圆的切点为D,连接OD,如图,
∵AC为圆的切线,
∴OD⊥AC,
∵AC=8,BC=6,AB=10,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴OD∥BC,且O为AB中点,
∴OD为△ABC的中位线,
∴ODBC=3,
同理可得POAC=4,
∴PQ=OP﹣OQ=4﹣3=1,
答案为:1.
三.解答题(共8小题,满分75分)
16.证明:如图,连接AD,
∵AB=CD,
∴,
∴,即,
∴∠BAD=∠CDA,
∴AE=DE,
又∵AB=CD,
∴EB=EC.
17.(1)如图:
证明:∵AD平分∠BAC,
∴∠1=∠2,
∵∠1=∠3,
∴∠2=∠3,
∵∠ABD=∠ABC+∠3,∠BED=∠ABC+∠2,
∴∠ABD=∠BED.
(2)解:连接OD,
∵∠AEB=125°,
∴∠AEC=55°,
∵AB为⊙O直径,
∴∠ACE=90°,
∴∠1=35°,
∴∠2=∠1=35°,
∴∠BOD=2∠2=70°,
∴的长π.
18.解:(1)如图,点M即为所求.
M(2,0),
(2)直线CD与圆M相切,
理由:圆M的半径CM2,
∵D(7,0),M(2,0),
∴OD=7,OM=2,
∴DM=7﹣2=5,CD,
∵CM2+CD2=20+5=25=52=DM2,
∴∠MCD=90°,
∴MC⊥CD,
∵MC是圆M的半径,
∴直线CD与圆M相切.
19.解:(1)连接OA,
∵AE是⊙O的切线,
∴∠OAE=90°,
∵AB=AE,
∴∠ABE=∠AEB,
∵OA=OB,
∴∠ABO=∠OAB,
∴∠OAB=∠ABE=∠E,
∵∠OAB+∠ABE+∠E+∠OAE=180°,
∴∠OAB=∠ABE=∠E=30°,
∴∠AOB=180°﹣∠OAB﹣∠ABO=120°,
∴∠ACB∠AOB=60°;
(2)设⊙O的半径为r,则OA=OD=r,OE=r+2,
∵∠OAE=90°,∠E=30°,
∴2OA=OE,即2r=r+2,
∴r=2,
⊙O的半径为2;
(3)∵∠AOB=120°,
∴∠AOE=60°,
∴AE=AO tan60°=2,
∴S阴影=S△OAE﹣S扇形AOD2×22π.
20.解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
由勾股定理得:AB10;
(2)连接OD,
∵∠ACB=90°,CD平分∠ACB,
∴∠ACDACB=45°,
∴∠AOD=2∠ACD=90°,
∵直径AB=10,
∴半径OA=OD=5,
∴阴影部分的面积S=S扇形AOD﹣S△AOD
.
21.解:(1)连接OC,
∵AF为圆O的切线,
∴AF⊥AB,
∵AB⊥CD,
∴AF∥CD,E为CD中点,即CE=DECD=2,
∵FC∥AD,
∴四边形ADCF为平行四边形,
∴FC=AD,AF=CD
在Rt△OCE中,设OC=OB=r,则OE=OB﹣EB=r﹣2,
根据勾股定理得:OC2=CE2+OE2,即r2=(2)2+(r﹣2)2,
解得:r=4,
∴AE=AO+OE=4+2=6,
在Rt△ADE中,AD4,
(2)∵AD4,CD=4,
∴AD=CD,
∵AF是⊙O切线,
∴AF⊥AB,
∵CD⊥AB,
∴AF∥CD,
∵CF∥AD,
∴四边形FADC是平行四边形,
∵AD=CD,
∴平行四边形FADC是菱形;
(3)连接OF,AC,
∵四边形FADC是菱形,
∴FA=FC,
∴∠FAC=∠FCA,
∵AO=CO,
∴∠OAC=∠OCA,
∴∠FAC+∠OAC=∠FCA+∠OCA,
即∠OCF=∠OAF=90°,
即OC⊥FC,
∵点C在⊙O上,
∴FC是⊙O的切线.
22.解:(1)设OA=OC=R m,
∵OA⊥CD,
∴CB=BDCD=14m,
在Rt△COB中,OC2=OB2+CB2,
∴R2=142+(R﹣12)2,
∴R,
∴OC14.2m.
(2)如图,补全⊙O,在CD的下方取一点N,连接CN,DN,CM,DM,
∵∠N∠COD=81°,
∵∠CMD+∠N=180°,
∴∠CMD=99°.
∵∠CMD=99°不变,是定值,
∴“齐天大圣”点M在洞顶上巡视时总能看清洞口CD的情况.
23.解:(1)∵∠APC是△PBC的一个外角,
∴∠C=∠APC﹣∠ABC=100°﹣63°=37°,
由圆周角定理得:∠BAD=∠C=37°,∠ADC=∠ABC=63°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=∠ADB﹣∠ADC=90°﹣63°=27°;
(2)连接OD,如图②所示:
∵CD⊥AB,
∴∠CPB=90°,
∴∠PCB=90°﹣∠ABC=90°﹣63°=27°,
∵DE是⊙O的切线,
∴DE⊥OD,
∴∠ODE=90°,
∵∠BOD=2∠PCB=54°,
∴∠E=90°﹣∠BOD=90°﹣54°=36°.
考试范围:24章 圆;考试时间:100分钟;总分:120
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.下列说法:
①直径是弦;②半圆是弧;③半径相等的两个圆是等圆;④长度相等的两条弧是等弧;
⑤在同圆中任意两条直径都互相平分.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
2.已知⊙O的半径为3cm,点A到圆心O的距离为4cm,则点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
3.如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
A.22° B.26° C.32° D.68°
4.如图,A是⊙O上一点,BC是直径,AC=2,AB=4,点D在⊙O上且平分,则DC的
长为( )
A. B. C. D.
(3题) (4题) (5题) (6题) (7题)
5.如图,圆O与正方形ABCD的两边AB、AD相切,且DE与圆O相切于E点.若圆O的半径为5,且AB=11,则DE的长度为何?( )
A.5 B.6 C. D.
6.如图,已知BC与⊙O相切于点B,CO的延长线交⊙O于点A,连接AB,若BC=2,AC=6,则⊙O的半径为( )
A.1.5 B.2 C.2.5 D.3
7.如图,在5×6的正方形网格中,若将△ABC绕着点A逆时针旋转得到△AB′C′,则的长为( )
A.π B. C.7π D.6π
8.如图,在△ABC中,∠ABC=90°,∠ACB=30°,AB=4,点O为BC的中点,以O为圆心,OB长为半径作半圆,交AC于点D,则图中阴影部分的面积是( )
A.5π B.54π C.52π D.102π
9.如图,在四边形材料ABCD中,AD∥BC,∠A=90°,AD=9cm,AB=20cm,BC=24cm.现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
A.cm B.8cm C.6cm D.10cm
10.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,与BC相交于点G,则下列结论:①∠BAD=∠CAD;②若∠BAC=60°,则∠BEC=120°;③若点G为BC的中点,则∠BGD=90°;④BD=DE.其中一定正确的个数是( )
A.1 B.2 C.3 D.4
(9题) (10题) (11题) (12题) (13题)
二.填空题(共5小题,满分15分,每小题3分)
11.如图,AB是⊙O的直径,弦CD∥AB,若∠ABD=60°,则∠ADC的度数是 .
12.如图,正六边形ABCDEF内接于⊙O.若直线PA与⊙O相切于点A,则∠PAB= .
13.如图所示,Rt△ABC中,∠B=90°,AC=12cm,BC=5cm.将其绕直角边AB所在的直线旋转一周得到一个圆锥,则这个圆锥的侧面积为 cm2.
14.在直径为10cm的⊙O中,弦AB的长为5cm,则AB所对的圆周角是 .
15.如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是 .
三.解答题(共8小题,满分75分)
16.(8分)如图,圆中两条弦AB、CD相交于点E,且AB=CD,求证:EB=EC.
17.(8分)如图,△ABC是⊙O的内接三角形,AB为⊙O直径,AB=6,AD平分∠BAC,交BC于点E,交⊙O于点D,连接BD.
(1)求证:∠ABD=∠BED;
(2)若∠AEB=125°,求的长(结果保留π).
18.(9分)在平面直角坐标系中,已知点A(0,4),B(4,4),C(6,2).
(1)请确定经过点A,B,C的圆弧所在圆的圆心M的位置,并写出点M的坐标;
(2)若一个点D(7,0),试判断直线CD与圆M的位置关系,并说明理由.
19.(9分)如图,⊙O是△ABC的外接圆,其切线AE与直径BD的延长线相交于点E,且AE=AB.
(1)求∠ACB的度数;
(2)若DE=2,求⊙O的半径.
(3)在(2)的前提下,求阴影部分面积.
20.(9分)如图,AB是⊙O的直径,弦AC=6,BC=8,∠ACB的平分线交⊙O于点D,连接AD.
(1)求直径AB的长;
(2)求阴影部分的面积.(结果保留π)
21.(9分)如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为点E,过点C作DA的平行线与AF相交于点F,CD=4,BE=2.
(1)求AD的长;
(2)求证:四边形FADC是菱形;
(3)求证:FC是⊙O的切线.
22.(11分)牂牁江“余月郎山,西陵晚渡”的风景描绘中有半个月亮挂在山上,月亮之上有个“齐天大圣”守护洞口的传说.真实情况是老王山上有个月亮洞,洞顶上经常有猴子爬来爬去,如图是月亮洞的截面示意图.
(1)科考队测量出月亮洞的洞宽CD约是28m,洞高AB约是12m,通过计算截面所在圆的半径可以解释月亮洞像半个月亮,求半径OC的长(结果精确到0.1m);
(2)若∠COD=162°,点M在上,求∠CMD的度数,并用数学知识解释为什么“齐天大圣”点M在洞顶上巡视时总能看清洞口CD的情况.
23.(12分)在⊙O中,弦CD与直径AB相交于点P,∠ABC=63°.
(Ⅰ)如图①,若∠APC=100°,求∠BAD和∠CDB的大小;
(Ⅱ)如图②,若CD⊥AB,过点D作⊙O的切线,与AB的延长线相交于点E,求∠E的大小.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:①直径是弦,正确,符合题意;
②半圆是弧,正确,符合题意;
③半径相等的两个圆是等圆,正确,符合题意;
④长度相等的两条弧不一定是等弧,原命题错误,不符合题意;
⑤在同圆中任意两条直径都互相平分,正确,符合题意,
正确的有4个,
选:D.
2.解:OA>3cm,则点A与⊙O的位置关系是:点A在圆外.
选:C.
3.解:∵∠A与∠BOC是同弧所对的圆周角与圆心角,∠A=68°,
∴∠BOC=2∠A=136°.
∵OB=OC,
∴∠OBC22°.
选:A.
4.解:∵A是⊙O上一点,BC是直径,
∴∠BAC=∠BDC=90°,
在Rt△ABC中,AC=2,AB=4,
由勾股定理得:AB2+AC2=BC2,即BC2=22+42=20,
∵点D在⊙O上且平分弧BC,
∴BD=DC,
在Rt△BDC中,由勾股定理得:BD2+DC2=BC2,即2DC2=BC2=20,
解得:DC,
选:B.
5.解:
连接OM、ON,
∵四边形ABCD是正方形,
∴AD=AB=11,∠A=90°,
∵圆O与正方形ABCD的两边AB、AD相切,
∴∠OMA=∠ONA=90°=∠A,
∵OM=ON,
∴四边形ANOM是正方形,
∴AM=OM=5,
∵AD和DE与圆O相切,圆O的半径为5,
∴AM=5,DM=DE,
∴DE=11﹣5=6,
选:B.
6.解:连接OB,
∵BC与⊙O相切于点B,
∴OB⊥BC,
设⊙O的半径为r,
在Rt△OBC中,OB2+BC2=OC2,
即,
解得:r=2,
选:B.
7.解:根据图示知,∠BAB′=45°,
∴的长为:π.
选:A.
8.解:连接OD.
在△ABC中,∠ABC=90°,∠ACB=30°,AB=4,
∴BCAB=4,
∴OC=OD=OB=2,
∴∠DOB=2∠C=60°,
∴S阴=S△ACB﹣S△COD﹣S扇形ODB4×4
=832π
=52π.
选:C.
9.解:如图,当AB,BC,CD相切于⊙O于点E,F,G时,⊙O的面积最大.连接OA,OB,OC,OD,OE,OF,OG,过点D作DH⊥BC于点H.
∵AD∥CB,∠BAD=90°,
∴∠ABC=90°,
∵∠DHB=90°,
∴四边形ABHD是矩形,
∴AB=DH=20cm,AD=BH=9cm,
∵BC=24cm,
∴CH=BC﹣BH=24﹣9=15(cm),
∴CD25(cm),
设OE=OF=OG=r cm,
则有(9+24)×2020×r24×r25×r9×(20﹣r),
∴r=8,
选:B.
10.解:∵E是△ABC的内心,
∴AD平分∠BAC,
∴∠BAD=∠CAD,①正确;
如图,连接BE,CE,
∵E是△ABC的内心,
∴∠EBC∠ABC,∠ECBACB,
∵∠BAC=60°,
∴∠ABC+∠ACB=120°,
∴∠BEC=180°﹣∠EBC﹣∠ECB=180°(∠ABC+∠ACB)=120°,②正确;
∵∠BAD=∠CAD,
∴,
∴OD⊥BC,
∵点G为BC的中点,
∴G一定在OD上,
∴∠BGD=90°,③正确;
如图,连接BE,
∴BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠DBC=∠DAC=∠BAD,
∴∠DBC+∠EBC=∠EBA+∠EAB,
∴∠DBE=∠DEB,
∴DB=DE,④正确.
∴一定正确的①②③④,共4个.
选:D.
二.填空题(共5小题,满分15分,每小题3分)
11.解:∵AB是⊙O的直径,
∴∠ADB=90°(直径所对的圆周角是直角);
又∵∠ABD=60°,
∴∠DAB=30°(直角三角形的两个锐角互余);
又∵CD∥AB,
∴∠ADC=∠DAB(两直线平行,内错角相等),
∴∠ADC=30°(等量代换).
答案为:30°.
12.解:连接OB,AD,BD,
∵多边形ABCDEF是正多边形,
∴AD为外接圆的直径,
∠AOB60°,
∴∠ADB∠AOB60°=30°.
∵直线PA与⊙O相切于点A,
∴∠PAB=∠ADB=30°.
答案为:30°.
13.解:圆锥的侧面积=π×5×12=60πcm2.
14.解:连接OA、OB,∠C和∠D为AB所对的圆周角,如图,
∵OA=OB=5,AB=5,
∴OA2+OB2=AB2,
∴△OAB为直角三角形,
∴∠AOB=90°,
∴∠C∠AOB=45°,
∴∠D=180°∠C=135°.
即AB所对的圆周角为45°或135°.
答案为45°或135°.
15.解:
当O、Q、P三点一线且OP⊥BC时,PQ有最小值,设AC与圆的切点为D,连接OD,如图,
∵AC为圆的切线,
∴OD⊥AC,
∵AC=8,BC=6,AB=10,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴OD∥BC,且O为AB中点,
∴OD为△ABC的中位线,
∴ODBC=3,
同理可得POAC=4,
∴PQ=OP﹣OQ=4﹣3=1,
答案为:1.
三.解答题(共8小题,满分75分)
16.证明:如图,连接AD,
∵AB=CD,
∴,
∴,即,
∴∠BAD=∠CDA,
∴AE=DE,
又∵AB=CD,
∴EB=EC.
17.(1)如图:
证明:∵AD平分∠BAC,
∴∠1=∠2,
∵∠1=∠3,
∴∠2=∠3,
∵∠ABD=∠ABC+∠3,∠BED=∠ABC+∠2,
∴∠ABD=∠BED.
(2)解:连接OD,
∵∠AEB=125°,
∴∠AEC=55°,
∵AB为⊙O直径,
∴∠ACE=90°,
∴∠1=35°,
∴∠2=∠1=35°,
∴∠BOD=2∠2=70°,
∴的长π.
18.解:(1)如图,点M即为所求.
M(2,0),
(2)直线CD与圆M相切,
理由:圆M的半径CM2,
∵D(7,0),M(2,0),
∴OD=7,OM=2,
∴DM=7﹣2=5,CD,
∵CM2+CD2=20+5=25=52=DM2,
∴∠MCD=90°,
∴MC⊥CD,
∵MC是圆M的半径,
∴直线CD与圆M相切.
19.解:(1)连接OA,
∵AE是⊙O的切线,
∴∠OAE=90°,
∵AB=AE,
∴∠ABE=∠AEB,
∵OA=OB,
∴∠ABO=∠OAB,
∴∠OAB=∠ABE=∠E,
∵∠OAB+∠ABE+∠E+∠OAE=180°,
∴∠OAB=∠ABE=∠E=30°,
∴∠AOB=180°﹣∠OAB﹣∠ABO=120°,
∴∠ACB∠AOB=60°;
(2)设⊙O的半径为r,则OA=OD=r,OE=r+2,
∵∠OAE=90°,∠E=30°,
∴2OA=OE,即2r=r+2,
∴r=2,
⊙O的半径为2;
(3)∵∠AOB=120°,
∴∠AOE=60°,
∴AE=AO tan60°=2,
∴S阴影=S△OAE﹣S扇形AOD2×22π.
20.解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
由勾股定理得:AB10;
(2)连接OD,
∵∠ACB=90°,CD平分∠ACB,
∴∠ACDACB=45°,
∴∠AOD=2∠ACD=90°,
∵直径AB=10,
∴半径OA=OD=5,
∴阴影部分的面积S=S扇形AOD﹣S△AOD
.
21.解:(1)连接OC,
∵AF为圆O的切线,
∴AF⊥AB,
∵AB⊥CD,
∴AF∥CD,E为CD中点,即CE=DECD=2,
∵FC∥AD,
∴四边形ADCF为平行四边形,
∴FC=AD,AF=CD
在Rt△OCE中,设OC=OB=r,则OE=OB﹣EB=r﹣2,
根据勾股定理得:OC2=CE2+OE2,即r2=(2)2+(r﹣2)2,
解得:r=4,
∴AE=AO+OE=4+2=6,
在Rt△ADE中,AD4,
(2)∵AD4,CD=4,
∴AD=CD,
∵AF是⊙O切线,
∴AF⊥AB,
∵CD⊥AB,
∴AF∥CD,
∵CF∥AD,
∴四边形FADC是平行四边形,
∵AD=CD,
∴平行四边形FADC是菱形;
(3)连接OF,AC,
∵四边形FADC是菱形,
∴FA=FC,
∴∠FAC=∠FCA,
∵AO=CO,
∴∠OAC=∠OCA,
∴∠FAC+∠OAC=∠FCA+∠OCA,
即∠OCF=∠OAF=90°,
即OC⊥FC,
∵点C在⊙O上,
∴FC是⊙O的切线.
22.解:(1)设OA=OC=R m,
∵OA⊥CD,
∴CB=BDCD=14m,
在Rt△COB中,OC2=OB2+CB2,
∴R2=142+(R﹣12)2,
∴R,
∴OC14.2m.
(2)如图,补全⊙O,在CD的下方取一点N,连接CN,DN,CM,DM,
∵∠N∠COD=81°,
∵∠CMD+∠N=180°,
∴∠CMD=99°.
∵∠CMD=99°不变,是定值,
∴“齐天大圣”点M在洞顶上巡视时总能看清洞口CD的情况.
23.解:(1)∵∠APC是△PBC的一个外角,
∴∠C=∠APC﹣∠ABC=100°﹣63°=37°,
由圆周角定理得:∠BAD=∠C=37°,∠ADC=∠ABC=63°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=∠ADB﹣∠ADC=90°﹣63°=27°;
(2)连接OD,如图②所示:
∵CD⊥AB,
∴∠CPB=90°,
∴∠PCB=90°﹣∠ABC=90°﹣63°=27°,
∵DE是⊙O的切线,
∴DE⊥OD,
∴∠ODE=90°,
∵∠BOD=2∠PCB=54°,
∴∠E=90°﹣∠BOD=90°﹣54°=36°.
同课章节目录
