第24章 圆 单元数学测试卷(含答案) 2024—2025学年人教版数学九年级上册
文档属性
| 名称 | 第24章 圆 单元数学测试卷(含答案) 2024—2025学年人教版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 578.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 08:01:03 | ||
图片预览




文档简介
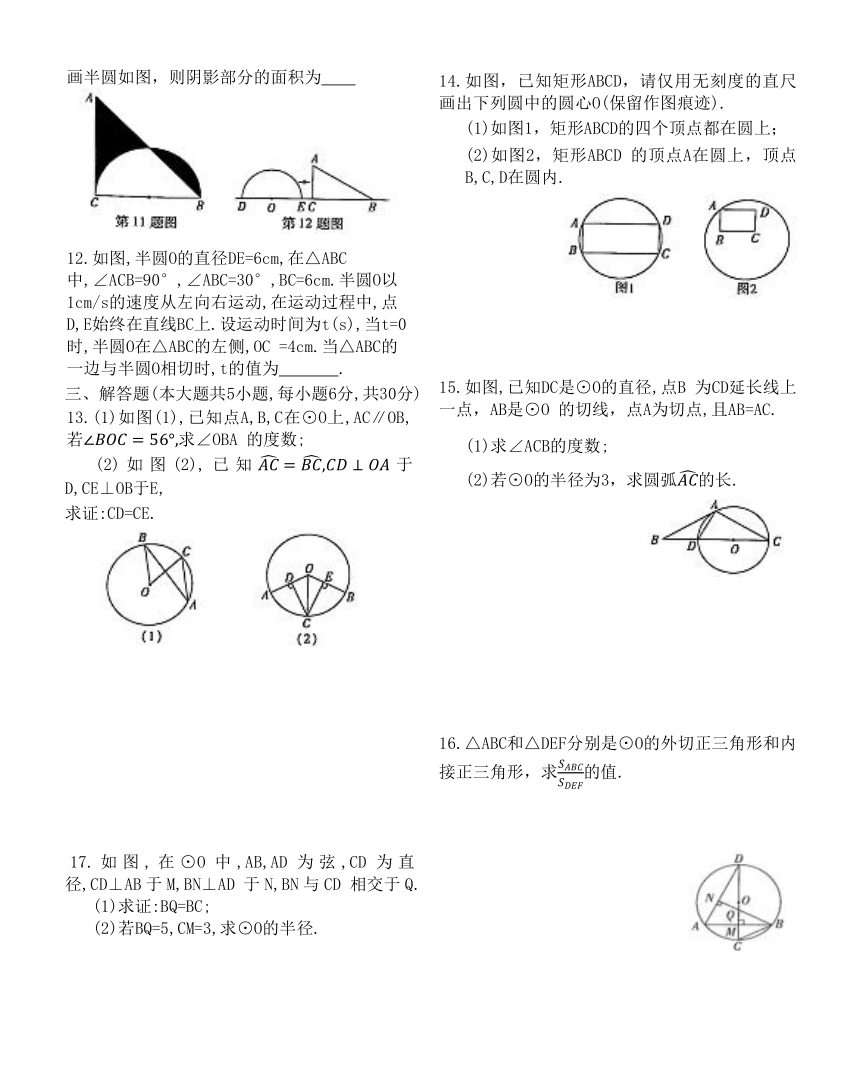
第二十四章综合测试卷
测试时间120分钟★满分120分
班级: 姓名: 得分:
一、选择题(本大题共6小题,每小题3分,共18分)
1.下列说法:(1)长度相等的弧是等弧,(2)相等的圆心角所对的弧相等,(3)劣弧一定比优弧短,(4)直径是圆中最长的弦.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.已知某直线到圆心的距离为5cm,圆的周长为10πcm,则这条直线与这个圆的公共点的个数为 ( )
A.0 B.1 C.2 D.无法确定
3.如图,CD为圆O的直径,弦AB⊥CD,垂足为E,CE =1,半径为25,则弦AB 的长为 ( )
A.24 B.14 C.10 D.7
4.如图,AB,AC是⊙O 的两条弦,OD⊥AB 于点 D,OE⊥AC于点E,连接OB,OC.若∠DOE=130°,则∠BOC的度数为 ( )
A.95° B.100° C.105° D.130°
5.如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为( )
A.16 B.14 C.12 D.10
6.如图,在△ABC中,∠BAC=90°,AB=AC=5,点D在AC上,且AD=2,点E是AB上的动点,连接DE,点F,G分别是BC,DE的中点,连接AG,FG,当AG=FG时,线段DE的长为 ( )
D.4
二、填空题(本大题共6小题,每小题3分,共18分)
7.如图,⊙O是△ABC 的外接圆,连接AO 并延长交⊙O 于点D,若∠C=50°,则∠BAD 的度数为 .
8.江南是水乡,如图,圆拱桥的拱顶到水面的距离CD为9m,水面宽AB为6m,则桥拱半径OC为 m.
9.如图,方老师用一张半径为18 cm的扇形纸板,做了一个圆锥形帽子(接缝忽略不计).如果圆锥形帽子的半径是10 cm,那么这张扇形纸板的面积是 cm (结果用含π的式子表示).
10.如图,等边三角形ABC的边长为1,以A为圆心,AC为半径画弧,交BA的延长线于D,再以B为圆心,BD为半径画弧,交CB 的延长线于E,再以C为圆心,CE为半径画弧,交AC的延长线于F,则由弧CD,弧DE,优弧EF及线段CF围成的图形(CDEFC)的周长为 .
11.若为直角三角形,AC=BC=4,以BC为直径画半圆如图,则阴影部分的面积为
12.如图,半圆O的直径DE=6cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=6cm.半圆O以1cm/s的速度从左向右运动,在运动过程中,点D,E始终在直线BC上.设运动时间为t(s),当t=0时,半圆O在△ABC的左侧,OC =4cm.当△ABC的一边与半圆O相切时,t的值为 .
三、解答题(本大题共5小题,每小题6分,共30分)
13.(1)如图(1),已知点A,B,C在⊙O上,AC∥OB,若求∠OBA 的度数;
(2)如图(2),已知于D,CE⊥OB于E,
求证:CD=CE.
14.如图,已知矩形ABCD,请仅用无刻度的直尺画出下列圆中的圆心O(保留作图痕迹).
(1)如图1,矩形ABCD的四个顶点都在圆上;
(2)如图2,矩形ABCD 的顶点A在圆上,顶点B,C,D在圆内.
15.如图,已知DC是⊙O的直径,点B 为CD延长线上一点,AB是⊙O 的切线,点A为切点,且AB=AC.
(1)求∠ACB的度数;
(2)若⊙O的半径为3,求圆弧的长.
16.△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,求的值.
17.如图,在⊙O中,AB,AD为弦,CD为直径,CD⊥AB于M,BN⊥AD 于N,BN与CD 相交于Q.
(1)求证:BQ=BC;
(2)若BQ=5,CM=3,求⊙O的半径.
四、解答题(本大题共3小题,每小题8分,共24分)
18.如图,D,E分别是⊙O 两条半径OA,OB 的中点,
(1)求证:CD=CE;
(2)若∠AOB=120°,OA=x,四边形ODCE的面积为y,求y与x的函数关系式.
19.如图,AB是⊙O 的直径,点C是⊙O上一点,连接BC,AC,点E是BC的中点,连接OE并延长交圆于点 D.
(1)求证:OD∥AC;
(2)若DE=2,BE=2 ,求阴影部分的面积.
20.如图,在△ABC中,AB=4,∠C=64°,以AB为直径的⊙O与AC 相交于点D,E为上一点,且∠ADE=40°.
(1)求的长;
(2)若∠EAD=76°,求证:CB为⊙O 的切线.
五、解答题(本大题共2小题,每小题9分,共18分)
21.已知平面直角坐标系中,点和直线Ax+By+C=0(其中A,B不全为0),则点P到直线Ax+By+C=0的距离d可用公式来计算.
例如:求点 P(1,2)到直线y=2x+1的距离,因为直线y=2x+1可化为2x-y+1=0,其中A =2,B=-1,C=1,所以点P(1,2)到直线y=2x+1的距离为:
根据以上材料,解答下列问题:
(1)求点M(0,3)到直线 的距离.
(2)在(1)的条件下,⊙M的半径判断⊙M与直线的位置关系,若相交,设其弦长为n,求n的值;若不相交,说明理由.
22.如图,在中,的平分线交BC于点D,点E在AB上,以AE为直径的⊙O恰好过点D.
(1)判断直线BC与⊙O 的位置关系,并说明理由.
(2)若
①求⊙O 的半径;
②求阴影部分的面积(结果保留π).
六、解答题(本大题共12分)
23.若一个四边形的两条对角线互相垂直且相等,则称这个四边形为奇妙四边形.如图①,四边形ABCD中,若则称四边形ABCD为奇妙四边形,根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质:奇妙四边形的面积等于两条对角线乘积的一半.根据以上信息回答:
(1)矩形 奇妙四边形(填“是”或“不是”);
(2)如图②,已知⊙O的内接四边形ABCD是奇妙四边形,若⊙O 的半径为6, 求奇妙四边形ABCD的面积;
(3)如图③,已知⊙O 的内接四边形ABCD是奇妙四边形,作于M,请猜测OM与AD的数量关系,并证明你的结论.
第二十四章综合测试卷答案
1. A 2. B 3. B 4. B 5. B
6.A〔提示:如图,连接DF,EF,过点 F 作 FN⊥AC于N,FM⊥AB 于 M,∵在△ABC中,∠BAC=90°,点 G 是 DE 的中点,∴ AG=DG=EG.又∵AG=FG,∴点A,D,F,E四点共圆,且 DE 是圆的直径,∴∠DFE =90°.∵ 在 Rt△ABC 中,AB =AC=5,点 F是 BC 的中点, 又∵ FN⊥AC,FM⊥AB,∠BAC =90°,∴ 四边形NAMF 是正方形, 又∵∠NFD +∠DFM =90°,∠DFM + ∠MFE = 90°,∴∠NFD = ∠MFE,∴ △NFD≌ 在 Rt△DAE中,
7.40° 8.5 9.180π 10.6π+3
11.4(提示:如图,设AB与半圆的交点为 D,连接 DC,∵ BC 是直径,∴ ∠BDC = 90°.∵∠ACB = 90°,AC = BC =4,∴∠DBC =∠DCB=45°,AD =BD. 过点 D 作 DE⊥BC,垂足为 E,则∠CDE=∠BDE=45°,∴CE = ∴半圆关于直线 DE 对称,∴阴影部分的面积等于
12.1或4或7〔提示:如图(1),当点E运动到点E与点C重合时,AC⊥OE,AC与半圆O 相切,此时半圆O 运动的距离为: 如图(2),当半圆O 与AB 相切于 F点时,连接OF,则 OB 此时点O 与点 C 重合,∴半圆O 运动的距离为4cm,∴t=4÷1=4.如图(3),当半圆O与AC 相切时,此时点 D与点 C 重合,半圆O运动的距离 7.综上,t的值为1或4或7.〕
13.(1)解: (2)证明:
14.解:(1)连接AC,BD,则AC 与 BD 的交点即为点 O,如图1.(2)延长AD交圆于点H,向两方延伸BC交圆于点M,N,连接MA,NH 并延长,交于点 E,连接MH,AN 交于点 F,延长AB 交圆于点G,连接GH,连接EF 并延长,交GH于点O 即为所求,如图2.
15.解:(1)连接OA,∵AB 是⊙O 的切线,点A 为切点,∴∠BAO =90°.又∵AB=AC,OA=OC,∴ ∠B=∠ACB =∠OAC.设∠ACB =x°,则在△ABC中,x°+x°+x°+90°=180°,解得x=30,∴ ∠ACB的度数为30°. (2)∵ ∠ACB =∠OAC =30°,∴∠AOC =120°,
16.解:如图,设 DE∥BC,过点 O 作 ON⊥BC,垂足为N,交 DE于点 M,连接OB,则O,D,B三点共线,设OM =1,则 OD = ON =2. ∵∠ODM = ∠OBN
17.(1)证明:∵CD⊥AB 于M,BN⊥AD 于N,∴∠BNA =∠BMQ = ∠A,∴∠C=∠BQM,∴BQ =BC. (2)解:由(1)得 BC=BQ =5,∠BMC=∠BMQ =90°,∴ 在 Rt△BMC 中, 连接BO,设BO=r,则OM=r-3,∴在Rt△BMO中, 即 解得 即⊙O 的半径为
18.(1)证明:连接OC, ,E分别是⊙O两条半径OA,OB 的中点,∴OD =OE. 在△COD 和△COE中,
(2)解:连接AC,∵∠AOB =120°,∴ ∠AOC =60°.又 OA =OC,∴△AOC为等边三角形.∵ 点 D 是OA 的中点,∴ CD⊥OA,OD= 在 Rt△COD 中,根据勾股定理得 .四边形ODCE的面积为
19.(1)证明:∵AB是⊙O 的直径,∴∠ACB=90°.∵点E是BC的中点,∴BE=CE,∴ OD⊥BC,∴ ∠BEO=90°,∴ ∠ACB =∠BEO,∴OD∥AC. (2)解:连接OC,设OB=OD=r,∵DE=2,∴OE= 解得r=4, 60°,∴阴影部分的面积=S扇形OAC-S△AOC=
20.(1)解:连接OE,∵ ∠ADE = 40°,∴ ∠AOE =2∠ADE =80°,∴∠EOB=180°-∠AOE=100°.∵AB=4,∴⊙O 的半径长是2, 的长 (2)证明: 50°,∴∠BAC=∠EAD - ∠EAB =76°--50°=26°.∵ ∠C =64°,∴∠C+∠BAC =90°,∴∠ABC=180°-(∠C+∠BAC) =90°,∴直径AB⊥BC,∴CB 为⊙O 的切线.
21.解: 可变形为 其中 -1,C=9,∴由公式可得 ∴点M到直线 的距离为3. (2)由(1)可知圆心到直线的距离d=3,圆的半径 . 直线与圆相交,则弦长 n =2×
22.解:(1)直线 BC 与⊙O 相切.理由如下:连接OD.∵ OA =OD,∴∠OAD = ∠ADO. ∵ AD 平分∠BAC,∴ ∠CAD = ∠DAO,∴∠DAC=∠ADO,∴ AC∥OD,∴ ∠BDO =∠C =90°.∵OD是⊙O 的半径,∴ 直线 BC 与⊙O 相切.
(2)①∵∠BDO =90°, 解得OD=2,∴⊙O的半径为2. ②∵OD=OE=2,BE= ∴ △ODE是等边三角形,∴阴影部分的面积为
23.解:(1)不是 (2)连接OB,OD,作OH⊥BD 于H,如图(1),则
BH=DH.∵ ∠BOD=2∠BCD=2×60°=120°,∴在等腰三角形OBD中,∠OBD =30°.在 Rt△OBH 中,∵∠OBH =30°,∴ OH= 四边形AB-CD 是奇妙四边形,. 证明如下:连接OB,OC,OA,OD,作 OE⊥AD 于E,如图
(2),∵OE⊥AD, ∴在等腰三角形AOD 中, 又∵
同理可得
⊥AC,∴ ∠BAC + ∠ABD = 90°,∴∠BOM + ∠AOE = 90°.
∵∠BOM+∠OBM=90°,∴∠OBM =∠AOE.在 和 中,
AE,
测试时间120分钟★满分120分
班级: 姓名: 得分:
一、选择题(本大题共6小题,每小题3分,共18分)
1.下列说法:(1)长度相等的弧是等弧,(2)相等的圆心角所对的弧相等,(3)劣弧一定比优弧短,(4)直径是圆中最长的弦.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.已知某直线到圆心的距离为5cm,圆的周长为10πcm,则这条直线与这个圆的公共点的个数为 ( )
A.0 B.1 C.2 D.无法确定
3.如图,CD为圆O的直径,弦AB⊥CD,垂足为E,CE =1,半径为25,则弦AB 的长为 ( )
A.24 B.14 C.10 D.7
4.如图,AB,AC是⊙O 的两条弦,OD⊥AB 于点 D,OE⊥AC于点E,连接OB,OC.若∠DOE=130°,则∠BOC的度数为 ( )
A.95° B.100° C.105° D.130°
5.如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为( )
A.16 B.14 C.12 D.10
6.如图,在△ABC中,∠BAC=90°,AB=AC=5,点D在AC上,且AD=2,点E是AB上的动点,连接DE,点F,G分别是BC,DE的中点,连接AG,FG,当AG=FG时,线段DE的长为 ( )
D.4
二、填空题(本大题共6小题,每小题3分,共18分)
7.如图,⊙O是△ABC 的外接圆,连接AO 并延长交⊙O 于点D,若∠C=50°,则∠BAD 的度数为 .
8.江南是水乡,如图,圆拱桥的拱顶到水面的距离CD为9m,水面宽AB为6m,则桥拱半径OC为 m.
9.如图,方老师用一张半径为18 cm的扇形纸板,做了一个圆锥形帽子(接缝忽略不计).如果圆锥形帽子的半径是10 cm,那么这张扇形纸板的面积是 cm (结果用含π的式子表示).
10.如图,等边三角形ABC的边长为1,以A为圆心,AC为半径画弧,交BA的延长线于D,再以B为圆心,BD为半径画弧,交CB 的延长线于E,再以C为圆心,CE为半径画弧,交AC的延长线于F,则由弧CD,弧DE,优弧EF及线段CF围成的图形(CDEFC)的周长为 .
11.若为直角三角形,AC=BC=4,以BC为直径画半圆如图,则阴影部分的面积为
12.如图,半圆O的直径DE=6cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=6cm.半圆O以1cm/s的速度从左向右运动,在运动过程中,点D,E始终在直线BC上.设运动时间为t(s),当t=0时,半圆O在△ABC的左侧,OC =4cm.当△ABC的一边与半圆O相切时,t的值为 .
三、解答题(本大题共5小题,每小题6分,共30分)
13.(1)如图(1),已知点A,B,C在⊙O上,AC∥OB,若求∠OBA 的度数;
(2)如图(2),已知于D,CE⊥OB于E,
求证:CD=CE.
14.如图,已知矩形ABCD,请仅用无刻度的直尺画出下列圆中的圆心O(保留作图痕迹).
(1)如图1,矩形ABCD的四个顶点都在圆上;
(2)如图2,矩形ABCD 的顶点A在圆上,顶点B,C,D在圆内.
15.如图,已知DC是⊙O的直径,点B 为CD延长线上一点,AB是⊙O 的切线,点A为切点,且AB=AC.
(1)求∠ACB的度数;
(2)若⊙O的半径为3,求圆弧的长.
16.△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,求的值.
17.如图,在⊙O中,AB,AD为弦,CD为直径,CD⊥AB于M,BN⊥AD 于N,BN与CD 相交于Q.
(1)求证:BQ=BC;
(2)若BQ=5,CM=3,求⊙O的半径.
四、解答题(本大题共3小题,每小题8分,共24分)
18.如图,D,E分别是⊙O 两条半径OA,OB 的中点,
(1)求证:CD=CE;
(2)若∠AOB=120°,OA=x,四边形ODCE的面积为y,求y与x的函数关系式.
19.如图,AB是⊙O 的直径,点C是⊙O上一点,连接BC,AC,点E是BC的中点,连接OE并延长交圆于点 D.
(1)求证:OD∥AC;
(2)若DE=2,BE=2 ,求阴影部分的面积.
20.如图,在△ABC中,AB=4,∠C=64°,以AB为直径的⊙O与AC 相交于点D,E为上一点,且∠ADE=40°.
(1)求的长;
(2)若∠EAD=76°,求证:CB为⊙O 的切线.
五、解答题(本大题共2小题,每小题9分,共18分)
21.已知平面直角坐标系中,点和直线Ax+By+C=0(其中A,B不全为0),则点P到直线Ax+By+C=0的距离d可用公式来计算.
例如:求点 P(1,2)到直线y=2x+1的距离,因为直线y=2x+1可化为2x-y+1=0,其中A =2,B=-1,C=1,所以点P(1,2)到直线y=2x+1的距离为:
根据以上材料,解答下列问题:
(1)求点M(0,3)到直线 的距离.
(2)在(1)的条件下,⊙M的半径判断⊙M与直线的位置关系,若相交,设其弦长为n,求n的值;若不相交,说明理由.
22.如图,在中,的平分线交BC于点D,点E在AB上,以AE为直径的⊙O恰好过点D.
(1)判断直线BC与⊙O 的位置关系,并说明理由.
(2)若
①求⊙O 的半径;
②求阴影部分的面积(结果保留π).
六、解答题(本大题共12分)
23.若一个四边形的两条对角线互相垂直且相等,则称这个四边形为奇妙四边形.如图①,四边形ABCD中,若则称四边形ABCD为奇妙四边形,根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质:奇妙四边形的面积等于两条对角线乘积的一半.根据以上信息回答:
(1)矩形 奇妙四边形(填“是”或“不是”);
(2)如图②,已知⊙O的内接四边形ABCD是奇妙四边形,若⊙O 的半径为6, 求奇妙四边形ABCD的面积;
(3)如图③,已知⊙O 的内接四边形ABCD是奇妙四边形,作于M,请猜测OM与AD的数量关系,并证明你的结论.
第二十四章综合测试卷答案
1. A 2. B 3. B 4. B 5. B
6.A〔提示:如图,连接DF,EF,过点 F 作 FN⊥AC于N,FM⊥AB 于 M,∵在△ABC中,∠BAC=90°,点 G 是 DE 的中点,∴ AG=DG=EG.又∵AG=FG,∴点A,D,F,E四点共圆,且 DE 是圆的直径,∴∠DFE =90°.∵ 在 Rt△ABC 中,AB =AC=5,点 F是 BC 的中点, 又∵ FN⊥AC,FM⊥AB,∠BAC =90°,∴ 四边形NAMF 是正方形, 又∵∠NFD +∠DFM =90°,∠DFM + ∠MFE = 90°,∴∠NFD = ∠MFE,∴ △NFD≌ 在 Rt△DAE中,
7.40° 8.5 9.180π 10.6π+3
11.4(提示:如图,设AB与半圆的交点为 D,连接 DC,∵ BC 是直径,∴ ∠BDC = 90°.∵∠ACB = 90°,AC = BC =4,∴∠DBC =∠DCB=45°,AD =BD. 过点 D 作 DE⊥BC,垂足为 E,则∠CDE=∠BDE=45°,∴CE = ∴半圆关于直线 DE 对称,∴阴影部分的面积等于
12.1或4或7〔提示:如图(1),当点E运动到点E与点C重合时,AC⊥OE,AC与半圆O 相切,此时半圆O 运动的距离为: 如图(2),当半圆O 与AB 相切于 F点时,连接OF,则 OB 此时点O 与点 C 重合,∴半圆O 运动的距离为4cm,∴t=4÷1=4.如图(3),当半圆O与AC 相切时,此时点 D与点 C 重合,半圆O运动的距离 7.综上,t的值为1或4或7.〕
13.(1)解: (2)证明:
14.解:(1)连接AC,BD,则AC 与 BD 的交点即为点 O,如图1.(2)延长AD交圆于点H,向两方延伸BC交圆于点M,N,连接MA,NH 并延长,交于点 E,连接MH,AN 交于点 F,延长AB 交圆于点G,连接GH,连接EF 并延长,交GH于点O 即为所求,如图2.
15.解:(1)连接OA,∵AB 是⊙O 的切线,点A 为切点,∴∠BAO =90°.又∵AB=AC,OA=OC,∴ ∠B=∠ACB =∠OAC.设∠ACB =x°,则在△ABC中,x°+x°+x°+90°=180°,解得x=30,∴ ∠ACB的度数为30°. (2)∵ ∠ACB =∠OAC =30°,∴∠AOC =120°,
16.解:如图,设 DE∥BC,过点 O 作 ON⊥BC,垂足为N,交 DE于点 M,连接OB,则O,D,B三点共线,设OM =1,则 OD = ON =2. ∵∠ODM = ∠OBN
17.(1)证明:∵CD⊥AB 于M,BN⊥AD 于N,∴∠BNA =∠BMQ = ∠A,∴∠C=∠BQM,∴BQ =BC. (2)解:由(1)得 BC=BQ =5,∠BMC=∠BMQ =90°,∴ 在 Rt△BMC 中, 连接BO,设BO=r,则OM=r-3,∴在Rt△BMO中, 即 解得 即⊙O 的半径为
18.(1)证明:连接OC, ,E分别是⊙O两条半径OA,OB 的中点,∴OD =OE. 在△COD 和△COE中,
(2)解:连接AC,∵∠AOB =120°,∴ ∠AOC =60°.又 OA =OC,∴△AOC为等边三角形.∵ 点 D 是OA 的中点,∴ CD⊥OA,OD= 在 Rt△COD 中,根据勾股定理得 .四边形ODCE的面积为
19.(1)证明:∵AB是⊙O 的直径,∴∠ACB=90°.∵点E是BC的中点,∴BE=CE,∴ OD⊥BC,∴ ∠BEO=90°,∴ ∠ACB =∠BEO,∴OD∥AC. (2)解:连接OC,设OB=OD=r,∵DE=2,∴OE= 解得r=4, 60°,∴阴影部分的面积=S扇形OAC-S△AOC=
20.(1)解:连接OE,∵ ∠ADE = 40°,∴ ∠AOE =2∠ADE =80°,∴∠EOB=180°-∠AOE=100°.∵AB=4,∴⊙O 的半径长是2, 的长 (2)证明: 50°,∴∠BAC=∠EAD - ∠EAB =76°--50°=26°.∵ ∠C =64°,∴∠C+∠BAC =90°,∴∠ABC=180°-(∠C+∠BAC) =90°,∴直径AB⊥BC,∴CB 为⊙O 的切线.
21.解: 可变形为 其中 -1,C=9,∴由公式可得 ∴点M到直线 的距离为3. (2)由(1)可知圆心到直线的距离d=3,圆的半径 . 直线与圆相交,则弦长 n =2×
22.解:(1)直线 BC 与⊙O 相切.理由如下:连接OD.∵ OA =OD,∴∠OAD = ∠ADO. ∵ AD 平分∠BAC,∴ ∠CAD = ∠DAO,∴∠DAC=∠ADO,∴ AC∥OD,∴ ∠BDO =∠C =90°.∵OD是⊙O 的半径,∴ 直线 BC 与⊙O 相切.
(2)①∵∠BDO =90°, 解得OD=2,∴⊙O的半径为2. ②∵OD=OE=2,BE= ∴ △ODE是等边三角形,∴阴影部分的面积为
23.解:(1)不是 (2)连接OB,OD,作OH⊥BD 于H,如图(1),则
BH=DH.∵ ∠BOD=2∠BCD=2×60°=120°,∴在等腰三角形OBD中,∠OBD =30°.在 Rt△OBH 中,∵∠OBH =30°,∴ OH= 四边形AB-CD 是奇妙四边形,. 证明如下:连接OB,OC,OA,OD,作 OE⊥AD 于E,如图
(2),∵OE⊥AD, ∴在等腰三角形AOD 中, 又∵
同理可得
⊥AC,∴ ∠BAC + ∠ABD = 90°,∴∠BOM + ∠AOE = 90°.
∵∠BOM+∠OBM=90°,∴∠OBM =∠AOE.在 和 中,
AE,
同课章节目录
