第五章 万有引力定律-开普勒定律与万有引力定律 (共32张PPT) 2025年高考物理基础专项复习
文档属性
| 名称 | 第五章 万有引力定律-开普勒定律与万有引力定律 (共32张PPT) 2025年高考物理基础专项复习 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-21 09:05:54 | ||
图片预览











文档简介
(共32张PPT)
第五章 万有引力定律
2025年高考物理一轮基础知识复习
开普勒定律与万有引力定律
目录
开普勒三大定律的理解与应用
万有引力定律的理解
双星、多星模型
壹
贰
叁
开普勒三大定律的理解与应用
壹
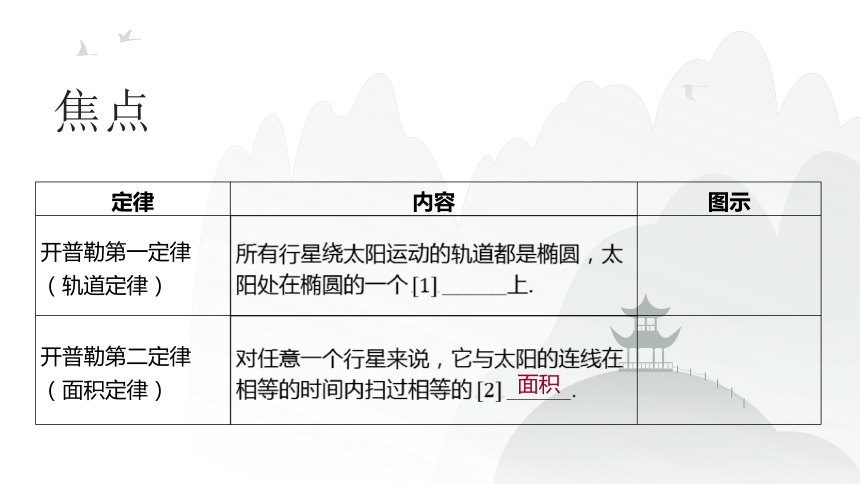
定律 内容 图示
开普勒第一定律(轨道定律) 所有行星绕太阳运动的轨道都是椭圆,太 阳处在椭圆的一个
开普勒第二定律(面积定律) 对任意一个行星来说,它与太阳的连线在 相等的时间内扫过相等的
面积
焦点
定律 内容 图示
开普勒第三定律(周期定律) 所有行星的轨道的
半长轴
公转周期
续表
(3)开普勒第三定律
说明(1)开普勒行星运动定律也适用于其他天体,例如月球、卫星绕地球的运动.
(2)由开普勒第二定律可得
远日点速度最小.
1.[粤教版必修二P75第2题设问变式]北京冬奥会开幕式二十四节气倒计时惊艳全球,如图
是地球沿椭圆轨道绕太阳运行所处不同位置对应的节气,下列说法正确的是( )
C
A.夏至时地球与太阳的连线在单位时间内扫过的面积最大
B.从冬至到春分的运行时间等于从春分到夏至的运行时间
C.太阳既在地球公转轨道的焦点上,也在火星公转轨道的焦点上
D.若用代表椭圆轨道的半长轴,代表公转周期,根据开普勒第三定律有 ,则地球和
火星环绕太阳运动对应的 值不同
【解析】由开普勒第二定律可知地球与太阳的连线在单位时间内扫过的面积都相等,故A错误;冬至为近日点,运
行速度最大,夏至为远日点,运行速度最小,所以从冬至到春分的运行时间小于从春分到夏至的运行时间,故B错
误;根据开普勒第一定律可知,太阳既在地球公转轨道的焦点上,也在火星公转轨道的焦点上,故C正确;根据开
普勒第三定律有,由于地球和火星环绕同一中心天体运动,则其对应的 值是相同的,故D错误。
2.[鲁科版必修二P93第5题角度变式]2023年4月12日,水星抵达东大距的位置。
由于水星是地内行星,平时都在太阳附近难以观察,从地球看出去,水星和太阳
的夹角(也称距角)达到最大夹角 (大距)时,观测时机最佳,如图所示。
若将水星与地球的公转均视为圆周运动,地球公转周期约为水星公转周期的4倍,
则水星在东大距时的距角 的正弦值 为( )
B
A. B. C. D.
【解析】根据开普勒第三定律有,根据几何关系有,又,联立解得 ,故选
B。
万有引力定律的理解
贰
1.万有引力定律的理解及应用
(1)表达式:
(2)适用条件:适用于相距很远,可以视为质点的物体之间的相互作用.质量分布
均匀的球体可以认为质量集中于球心,也可用此公式计算,其中
距离.
2.行星动力学规律
(1)天上:万有引力提供向心力,则
3.星体表面及上空的重力加速度
(1)地球表面附近的重力加速度
(2)地球上空距离地心
4.万有引力的“两个推论”
推论1:在均质球壳的空腔内任意位置处,质点受到球壳的万有引力的合力为零,即
推论2:如图所示,在均质球体内部距离球心
体内半径为
重力与万有引力的关系
(1)在地球表面上的物体所受的万有引力F可以分解成物体所受的重力G和随地球自转而做圆周运动的向心力F',如图所示。其中F=G,而F'=mrω2。
(2)当物体在赤道上时,F、G、F'三力同向,此时F'达到最大值,F'max=mRω2,重力达到最小值,Gmin=F-F'=G-mRω2。
(3)当物体在两极的极点时,F'=0,F=G,此时重力等于万有引力,重力达到最大值,Gmax=G。
(4)物体由赤道向两极移动,向心力减小,重力增大,只有在两极时物体所受的万有引力才等于重力。总之,无论如何,都不能说重力就是万有引力。
1.[链接人教版必修二P50知识,2023山东卷]牛顿认为物体落地是由于地球对物体的吸引,这种吸引力可能与天体
间(如地球与月球)的引力具有相同的性质,且都满足。已知地月之间的距离 大约是地球半径的60倍,地
球表面的重力加速度为 ,根据牛顿的猜想,月球绕地球公转的周期为( )
C
A. B. C. D.
【解析】设地球质量为,月球质量为,地球半径为,依题意有 ,对月球绕地球的匀速圆周运动,有
,对在地球表面附近的物体,有,即 ,解得月球绕地球的公转周期
,C正确。
2.[多选][鲁科版必修二P112第6题拓展变式]“天问一号”环绕器在火星探测任务中,分饰了飞行器、通信器和
探测器三大角色,创下多项国内外纪录。若已知环绕器绕火星做匀速圆周运动的轨道半径为、周期为 ,火星的
半径为,引力常量为 ,则可以推算出( )
AD
A.火星的质量为 B.环绕器的质量为
C.火星表面的重力加速度大小为 D.火星的密度为
【解析】环绕器绕火星做匀速圆周运动,由万有引力提供向心力,可得 ,解得火星的质量为
,环绕器的质量无法求出,故A正确,B错误;由黄金代换式可得,联立解得 ,故C
错误;火星的密度为,又,联立解得 ,故D正确。
3.[人教版必修二P58第1题情境变式]2022年7月29日,电影《独行月球》上映。电影中,维修工“独孤月”驾驶月
球车从高为的悬崖一侧水平飞出,飞出时的速度为。已知地球半径是月球半径的 倍,地球质量是月球质量的
倍,地球表面重力加速度大小为 。忽略地球与月球自转的影响,则“独孤月”从飞出到落到月面上的时间为 ( )
D
A. B. C. D.
【解析】在地球表面,质量为的物体所受重力满足,可得地球表面的重力加速度 ,同理月球表
面的重力加速度,则,解得,由 ,可得月球车从飞出到落到月面上的
时间 ,故选D。
4.[粤教版必修二P75第3题角度变式] 2022年5月10日01时56分,天舟四号货运飞船成功相会天和核心舱,
天和核心舱距离地面约,地球北极的重力加速度为,地球赤道表面的重力加速度为 ,地球自转
的周期为,天和核心舱轨道为正圆,根据题目的已知条件(引力常量 未知),下列说法错误的是( )
B
A.可以求出天舟四号的线速度 B.可以求出地球的质量
C.可以求出地球的半径 D.可以求出天舟四号的周期
【解析】由于赤道和两极处的重力加速度不同,所以有 (【点拨】物体的万有引力与物体在
两级的重力相等,且在赤道上万有引力与重力之差提供物体随地球自转的向心力。),解得地球半径
,选项C正确,不符合题意;地球北极的重力加速度为,有,由于不知道 (【易错】
容易定性思维,误以为是已知的。),所以无法求出地球的质量,选项B错误,符合题意;根据
和,可以求出天舟四号的线速度,选项A正确,不符合题意;同理,由 和
,可以求出天舟四号的周期,选项D正确,不符合题意。
双星、多星模型
叁
1.双星模型
(1)各自需要的向心力由彼此间的万有引力提供,即
(2)两颗星的周期及角速度都相同,即
(3)两颗星的轨道半径与它们之间的距离关系为
(4)两颗星到轨道圆心的距离
(5)双星的运行周期
(6)双星的总质量
2.多星模型
分析处理多星问题,必须明确所研究星体所受的万有引力的合力提供其做圆周运动的向心力.除中心星体外,各星体的角速度和周期相等.
(1)已观测到稳定的三星系统存在的形式有:
①三颗星位于同一直线上,两颗环绕星体围绕中心星体在同一半径为
上运行,如图甲所示.
②三颗质量均为
(2)宇宙中存在一些离其他恒星很远的四颗恒星组成的四星系统,通常可忽略其他星体对它们的引力作用.稳定的四星系统存在多种形式:
①四颗质量相等的恒星位于正方形的四个顶点上,沿外接于该正方形的圆形轨道做匀速圆周运动,如图丙所示.
②三颗恒星始终位于等边三角形的三个顶点上,另一颗恒星位于等边三角形的中心
1.[多选][鲁科版必修二P128科学书屋拓展变式]我国天文学家通过“天眼”(射电望远镜)
在武仙座球状星团中发现一个脉冲双星系统。如图所示,由恒星与恒星 组成的双星系
统绕其连线上的点做匀速圆周运动,若恒星的质量为,恒星的质量为,、 之间
的距离为,引力常量为 。下列说法正确的是( )
BD
A.恒星的角速度大于恒星的角速度 B.恒星与恒星的线速度之比为
C.恒星到点的距离为 D.恒星的运行周期为
【解析】双星系统中两颗星的角速度一定相等,A错误;对恒星有 ,对
恒星有,解得,又由于,解得, ,C错
误;根据,解得,B正确;恒星的运行周期为 ,D正确。
2.宇宙中存在一些离其他恒星较远的三星系统,通常可忽略其他星体对它们的引力作用。现已观测到稳定的三星系
统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星做圆周运动,如图甲所示;另一
种是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行,如图乙所示。设两种系统中
三个星体的质量均为,且两种系统中各星间的距离已在图中标出,引力常量为 ,则下列说法正确的是( )
D
图甲
图乙
A.直线形三星系统中星体做圆周运动的线速度大小为
B.直线形三星系统中星体做圆周运动的周期为
C.三角形三星系统中每颗星做圆周运动的角速度为
D.三角形三星系统中每颗星做圆周运动的加速度大小为
【解析】在直线三星系统中,外面的星体绕中心天体做圆周运动的向心力由其受到的另外两个天体的万有引力的
合力提供,即,解得,选项A错误。若用周期来表达则有 ,
,选项B错误。在三角形三星系统中,每个星体受到的万有引力的合力提供向心力,围绕其几何中心
即三角形的中心做匀速圆周运动,受力分析如图所示。向心力的大小为,做圆周运动的半径为 ,因此
有,解得, ,选项C错误,D正确。
3.[鲁科版必修二P111第1题模型变式]离其他恒星较远的四星系统的形式如图所示,三颗星体
位于边长为 的等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道做匀速圆周运动,
而位于三角形中心的第四颗星体刚好不动。设每颗星体的质量均为,引力常量为 ,则( )
D
A.位于等边三角形三个顶点上的每颗星体做圆周运动的向心加速度大小与 无关
B.顶点上的三星总动能为
C.若距离不变,四颗星体的质量均变为 ,则角速度变为原来的2倍
D.若四颗星体的质量均不变,距离均变为,则周期变为原来的 倍
【解析】根据万有引力定律及几何知识,可求得位于等边三角形三个顶点上的每颗星体做圆周运动的合外力
,根据牛顿第二定律可得,每颗星体的向心加速度大小
,故A错误;三星的总动能为,对每个星体有 ,由几何知识得
,联立解得 ,故B错误;结合选项A分析可知,位于三角形顶点上的每颗星体受到的合外力
,若距离不变,四颗星体的质量均变为 ,则顶点上的每颗星体受到的合力将变为原来的4倍,根据
可知,星体角速度将变为原来的倍,故C错误;根据 结合以上分析可知,星体做匀速
圆周运动的周期,若四颗星体的质量均不变,距离均变为,则周期变为原来的
倍,故D正确。
谢谢
第五章 万有引力定律
2025年高考物理一轮基础知识复习
开普勒定律与万有引力定律
目录
开普勒三大定律的理解与应用
万有引力定律的理解
双星、多星模型
壹
贰
叁
开普勒三大定律的理解与应用
壹
定律 内容 图示
开普勒第一定律(轨道定律) 所有行星绕太阳运动的轨道都是椭圆,太 阳处在椭圆的一个
开普勒第二定律(面积定律) 对任意一个行星来说,它与太阳的连线在 相等的时间内扫过相等的
面积
焦点
定律 内容 图示
开普勒第三定律(周期定律) 所有行星的轨道的
半长轴
公转周期
续表
(3)开普勒第三定律
说明(1)开普勒行星运动定律也适用于其他天体,例如月球、卫星绕地球的运动.
(2)由开普勒第二定律可得
远日点速度最小.
1.[粤教版必修二P75第2题设问变式]北京冬奥会开幕式二十四节气倒计时惊艳全球,如图
是地球沿椭圆轨道绕太阳运行所处不同位置对应的节气,下列说法正确的是( )
C
A.夏至时地球与太阳的连线在单位时间内扫过的面积最大
B.从冬至到春分的运行时间等于从春分到夏至的运行时间
C.太阳既在地球公转轨道的焦点上,也在火星公转轨道的焦点上
D.若用代表椭圆轨道的半长轴,代表公转周期,根据开普勒第三定律有 ,则地球和
火星环绕太阳运动对应的 值不同
【解析】由开普勒第二定律可知地球与太阳的连线在单位时间内扫过的面积都相等,故A错误;冬至为近日点,运
行速度最大,夏至为远日点,运行速度最小,所以从冬至到春分的运行时间小于从春分到夏至的运行时间,故B错
误;根据开普勒第一定律可知,太阳既在地球公转轨道的焦点上,也在火星公转轨道的焦点上,故C正确;根据开
普勒第三定律有,由于地球和火星环绕同一中心天体运动,则其对应的 值是相同的,故D错误。
2.[鲁科版必修二P93第5题角度变式]2023年4月12日,水星抵达东大距的位置。
由于水星是地内行星,平时都在太阳附近难以观察,从地球看出去,水星和太阳
的夹角(也称距角)达到最大夹角 (大距)时,观测时机最佳,如图所示。
若将水星与地球的公转均视为圆周运动,地球公转周期约为水星公转周期的4倍,
则水星在东大距时的距角 的正弦值 为( )
B
A. B. C. D.
【解析】根据开普勒第三定律有,根据几何关系有,又,联立解得 ,故选
B。
万有引力定律的理解
贰
1.万有引力定律的理解及应用
(1)表达式:
(2)适用条件:适用于相距很远,可以视为质点的物体之间的相互作用.质量分布
均匀的球体可以认为质量集中于球心,也可用此公式计算,其中
距离.
2.行星动力学规律
(1)天上:万有引力提供向心力,则
3.星体表面及上空的重力加速度
(1)地球表面附近的重力加速度
(2)地球上空距离地心
4.万有引力的“两个推论”
推论1:在均质球壳的空腔内任意位置处,质点受到球壳的万有引力的合力为零,即
推论2:如图所示,在均质球体内部距离球心
体内半径为
重力与万有引力的关系
(1)在地球表面上的物体所受的万有引力F可以分解成物体所受的重力G和随地球自转而做圆周运动的向心力F',如图所示。其中F=G,而F'=mrω2。
(2)当物体在赤道上时,F、G、F'三力同向,此时F'达到最大值,F'max=mRω2,重力达到最小值,Gmin=F-F'=G-mRω2。
(3)当物体在两极的极点时,F'=0,F=G,此时重力等于万有引力,重力达到最大值,Gmax=G。
(4)物体由赤道向两极移动,向心力减小,重力增大,只有在两极时物体所受的万有引力才等于重力。总之,无论如何,都不能说重力就是万有引力。
1.[链接人教版必修二P50知识,2023山东卷]牛顿认为物体落地是由于地球对物体的吸引,这种吸引力可能与天体
间(如地球与月球)的引力具有相同的性质,且都满足。已知地月之间的距离 大约是地球半径的60倍,地
球表面的重力加速度为 ,根据牛顿的猜想,月球绕地球公转的周期为( )
C
A. B. C. D.
【解析】设地球质量为,月球质量为,地球半径为,依题意有 ,对月球绕地球的匀速圆周运动,有
,对在地球表面附近的物体,有,即 ,解得月球绕地球的公转周期
,C正确。
2.[多选][鲁科版必修二P112第6题拓展变式]“天问一号”环绕器在火星探测任务中,分饰了飞行器、通信器和
探测器三大角色,创下多项国内外纪录。若已知环绕器绕火星做匀速圆周运动的轨道半径为、周期为 ,火星的
半径为,引力常量为 ,则可以推算出( )
AD
A.火星的质量为 B.环绕器的质量为
C.火星表面的重力加速度大小为 D.火星的密度为
【解析】环绕器绕火星做匀速圆周运动,由万有引力提供向心力,可得 ,解得火星的质量为
,环绕器的质量无法求出,故A正确,B错误;由黄金代换式可得,联立解得 ,故C
错误;火星的密度为,又,联立解得 ,故D正确。
3.[人教版必修二P58第1题情境变式]2022年7月29日,电影《独行月球》上映。电影中,维修工“独孤月”驾驶月
球车从高为的悬崖一侧水平飞出,飞出时的速度为。已知地球半径是月球半径的 倍,地球质量是月球质量的
倍,地球表面重力加速度大小为 。忽略地球与月球自转的影响,则“独孤月”从飞出到落到月面上的时间为 ( )
D
A. B. C. D.
【解析】在地球表面,质量为的物体所受重力满足,可得地球表面的重力加速度 ,同理月球表
面的重力加速度,则,解得,由 ,可得月球车从飞出到落到月面上的
时间 ,故选D。
4.[粤教版必修二P75第3题角度变式] 2022年5月10日01时56分,天舟四号货运飞船成功相会天和核心舱,
天和核心舱距离地面约,地球北极的重力加速度为,地球赤道表面的重力加速度为 ,地球自转
的周期为,天和核心舱轨道为正圆,根据题目的已知条件(引力常量 未知),下列说法错误的是( )
B
A.可以求出天舟四号的线速度 B.可以求出地球的质量
C.可以求出地球的半径 D.可以求出天舟四号的周期
【解析】由于赤道和两极处的重力加速度不同,所以有 (【点拨】物体的万有引力与物体在
两级的重力相等,且在赤道上万有引力与重力之差提供物体随地球自转的向心力。),解得地球半径
,选项C正确,不符合题意;地球北极的重力加速度为,有,由于不知道 (【易错】
容易定性思维,误以为是已知的。),所以无法求出地球的质量,选项B错误,符合题意;根据
和,可以求出天舟四号的线速度,选项A正确,不符合题意;同理,由 和
,可以求出天舟四号的周期,选项D正确,不符合题意。
双星、多星模型
叁
1.双星模型
(1)各自需要的向心力由彼此间的万有引力提供,即
(2)两颗星的周期及角速度都相同,即
(3)两颗星的轨道半径与它们之间的距离关系为
(4)两颗星到轨道圆心的距离
(5)双星的运行周期
(6)双星的总质量
2.多星模型
分析处理多星问题,必须明确所研究星体所受的万有引力的合力提供其做圆周运动的向心力.除中心星体外,各星体的角速度和周期相等.
(1)已观测到稳定的三星系统存在的形式有:
①三颗星位于同一直线上,两颗环绕星体围绕中心星体在同一半径为
上运行,如图甲所示.
②三颗质量均为
(2)宇宙中存在一些离其他恒星很远的四颗恒星组成的四星系统,通常可忽略其他星体对它们的引力作用.稳定的四星系统存在多种形式:
①四颗质量相等的恒星位于正方形的四个顶点上,沿外接于该正方形的圆形轨道做匀速圆周运动,如图丙所示.
②三颗恒星始终位于等边三角形的三个顶点上,另一颗恒星位于等边三角形的中心
1.[多选][鲁科版必修二P128科学书屋拓展变式]我国天文学家通过“天眼”(射电望远镜)
在武仙座球状星团中发现一个脉冲双星系统。如图所示,由恒星与恒星 组成的双星系
统绕其连线上的点做匀速圆周运动,若恒星的质量为,恒星的质量为,、 之间
的距离为,引力常量为 。下列说法正确的是( )
BD
A.恒星的角速度大于恒星的角速度 B.恒星与恒星的线速度之比为
C.恒星到点的距离为 D.恒星的运行周期为
【解析】双星系统中两颗星的角速度一定相等,A错误;对恒星有 ,对
恒星有,解得,又由于,解得, ,C错
误;根据,解得,B正确;恒星的运行周期为 ,D正确。
2.宇宙中存在一些离其他恒星较远的三星系统,通常可忽略其他星体对它们的引力作用。现已观测到稳定的三星系
统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星做圆周运动,如图甲所示;另一
种是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行,如图乙所示。设两种系统中
三个星体的质量均为,且两种系统中各星间的距离已在图中标出,引力常量为 ,则下列说法正确的是( )
D
图甲
图乙
A.直线形三星系统中星体做圆周运动的线速度大小为
B.直线形三星系统中星体做圆周运动的周期为
C.三角形三星系统中每颗星做圆周运动的角速度为
D.三角形三星系统中每颗星做圆周运动的加速度大小为
【解析】在直线三星系统中,外面的星体绕中心天体做圆周运动的向心力由其受到的另外两个天体的万有引力的
合力提供,即,解得,选项A错误。若用周期来表达则有 ,
,选项B错误。在三角形三星系统中,每个星体受到的万有引力的合力提供向心力,围绕其几何中心
即三角形的中心做匀速圆周运动,受力分析如图所示。向心力的大小为,做圆周运动的半径为 ,因此
有,解得, ,选项C错误,D正确。
3.[鲁科版必修二P111第1题模型变式]离其他恒星较远的四星系统的形式如图所示,三颗星体
位于边长为 的等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道做匀速圆周运动,
而位于三角形中心的第四颗星体刚好不动。设每颗星体的质量均为,引力常量为 ,则( )
D
A.位于等边三角形三个顶点上的每颗星体做圆周运动的向心加速度大小与 无关
B.顶点上的三星总动能为
C.若距离不变,四颗星体的质量均变为 ,则角速度变为原来的2倍
D.若四颗星体的质量均不变,距离均变为,则周期变为原来的 倍
【解析】根据万有引力定律及几何知识,可求得位于等边三角形三个顶点上的每颗星体做圆周运动的合外力
,根据牛顿第二定律可得,每颗星体的向心加速度大小
,故A错误;三星的总动能为,对每个星体有 ,由几何知识得
,联立解得 ,故B错误;结合选项A分析可知,位于三角形顶点上的每颗星体受到的合外力
,若距离不变,四颗星体的质量均变为 ,则顶点上的每颗星体受到的合力将变为原来的4倍,根据
可知,星体角速度将变为原来的倍,故C错误;根据 结合以上分析可知,星体做匀速
圆周运动的周期,若四颗星体的质量均不变,距离均变为,则周期变为原来的
倍,故D正确。
谢谢
同课章节目录
