2024—2025学年苏科版数学九年级上期末复习试题(含答案)
文档属性
| 名称 | 2024—2025学年苏科版数学九年级上期末复习试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 389.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 09:19:00 | ||
图片预览




文档简介
苏科版数学九年级上期末复习试题
一.选择题(共10小题)
1.一组数据为﹣1,2,3,4,6,6,从这组数据中抽取一个数,抽到的数为6的概率是( )
A. B. C. D.
2.样本数据2、a、3、4的平均数是3,则a的值是( )
A.1 B.2 C.3 D.4
3.下列各方程中,一定是一元二次方程的是( )
A. B.x2+5x﹣3=x(x﹣1) C.(x﹣2)2=2(x﹣2) D.x2+2y=3
4.如图,四边形ABCD外切于⊙O,且AB=10,CD=15,则四边形ABCD的周长为( )
A.60 B.55 C.45 D.50
5.用半径为60,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面半径是( )
A.10 B.20 C.30 D.40
6.若关于x的一元二次方程kx2﹣6x+3=0有两个不相等的实数根,则k的取值范围是( )
A.k>3 B.k≠0 C.k<3 D.k<3且k≠0
7.如图,CD是⊙O的直径,若AB⊥CD,垂足为B,∠OAB=40°,则∠C的度数为( )
A.25° B.20° C.10° D.30°
8.若x1,x2是方程5x2+x﹣5=0的两个根,则的值为( )
A.﹣1 B. C.5 D.
9.如图,圆锥的侧面展开图是一个圆心角为72°的扇形,若扇形的半径l是5,则该圆锥的体积是( )
A.π B.π C.2π D.π
10.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,与BC相交于点G,则下列结论:①∠BAD=∠CAD;②若∠BAC=50°,则∠BEC=130°;③若点G为BC的中点,则∠BGD=90°;④BD=DE.其中一定正确的个数是( )
A.1 B.2 C.3 D.4
二.填空题(共8小题)
11.一个不透明的盒子里有形状、大小相同的黄球2个、红球3个,从盒子里任意摸出1个球,摸到红球的概率是 .
12.若一组数据a1,a2,…,an的平均数为4,方差为3,那么数据2a1+3,2a2+3,…,2an+3的平均数和方差分别是 , .
13.已知关于x的方程(m+1)x|4m|﹣2+27mx+5=0是一元二次方程,则m= .
14.同一平面内,⊙O内一点P到圆上的最大距离为6cm,最小距离为2cm,则⊙O的半径为 cm.
15.如图,AB是⊙O的弦,半径OD⊥AB于点C,AE为直径,AB=8,CD=2,则线段CE的长为 .
16.某文具店为迎接“购物节”,提高水笔销量,经过两次降价后(每次降价的百分率相同),由每盒25元降至每盒16元.则降价的百分率为 .
17.如图,△ABC为⊙O的内接三角形,O为圆心,OD⊥AB于点D,OE⊥AC于点E,若DE=5,则BC= .
18.如图,在矩形ABCD中,AB=6,BC=4,P是矩形内部一动点,且满足∠BCP=∠PDC,则线段BP的最小值是 ;当BP取最小值时,DP延长线交线段BC于E,则CE的长为 .
三.解答题(共9小题)
19.解方程:
(1)x2﹣6x+5=0. (2)2x2+3x﹣5=0.
20.已知关于x的一元二次方程x2﹣4mx+m2=0.
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若x=2是该方程的根,求代数式(m﹣2)2﹣2(2m﹣3)的值.
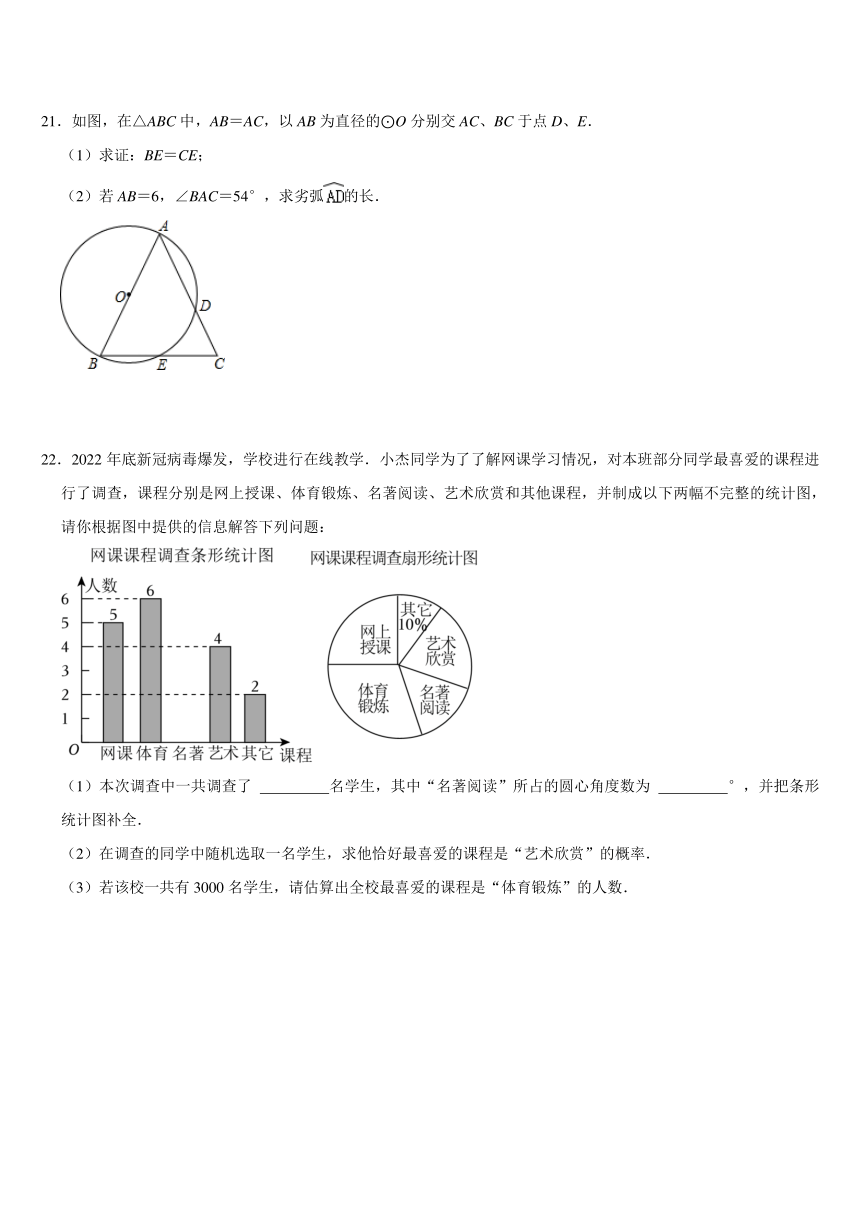
21.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.
(1)求证:BE=CE;
(2)若AB=6,∠BAC=54°,求劣弧的长.
22.2022年底新冠病毒爆发,学校进行在线教学.小杰同学为了了解网课学习情况,对本班部分同学最喜爱的课程进行了调查,课程分别是网上授课、体育锻炼、名著阅读、艺术欣赏和其他课程,并制成以下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)本次调查中一共调查了 名学生,其中“名著阅读”所占的圆心角度数为 °,并把条形统计图补全.
(2)在调查的同学中随机选取一名学生,求他恰好最喜爱的课程是“艺术欣赏”的概率.
(3)若该校一共有3000名学生,请估算出全校最喜爱的课程是“体育锻炼”的人数.
23.如图所示,等边△ABC内接于⊙O,D为圆周上一点.
(1)求证:BD平分∠ADC;
(2)若CD=2,AD=3,求BD的长度.
24.如图,AB是⊙O直径,点C在⊙O上,在AB的延长线上取一点D,连接CD,使∠BCD=∠A.
(1)求证:直线CD是⊙O的切线;
(2)若∠ACD=120°,AB=4,求图中阴影部分的面积.
25.为鼓励和推广全民阅读,某品牌图书开展了促销活动.八月份售出图书3000本,十月份售出图书4320本.
(1)求该品牌图书销量的月平均增长率;
(2)该品牌图书每本成本为20元,当售价为40元/本时,平均每天的销售量为100本.经试销统计发现,如果该品牌图书的售价每降价1元,那么平均每天可多售出10本.若要使平均每天的利润保持不变,并且让消费者尽可能获得实惠,那么该品牌图书每本的售价应为多少元?
26.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,垂足为点E,延长CA交⊙O于点F,连接BF.
(1)求证:DE是⊙O的切线;
(2)连接OE,若BF=,FC=10,求OE的长.
27.如图,在Rt△ABC中,∠C=90°,点O在AC上,以OA为半径的半圆O交AB于点D,交AC于点E,点F在BC上,且BF=DF.
(1)求证:DF是半圆O的切线;
(2)若AC=4,BC=3,CF=1,求半圆O的半径长.
参考答案
一.选择题(共10小题)
1.A.
2.C.
3.C.
4.D.
5.B.
6.D.
7.A.
8.D.
9.D.
10.C.
二.填空题(共8小题)
11..
12.11,12.
13.1.
14.4.
15.2.
16.20%.
17.10.
18.2;3.
三.解答题(共9小题)
19.解:(1)x2﹣6x+5=0,
(x﹣1)(x﹣5)=0,
x﹣1=0或x﹣5=0,
∴x1=1,x2=5;
(2)2x2+3x﹣5=0,
(2x+5)(x﹣1)=0,
2x+5=0或x﹣1=0,
∴,x2=1.
20.(1)证明:∵x2﹣4mx+m2=0,
∴a=1,b=﹣4m,c=m2,
∴Δ=(﹣4m)2﹣4m2=12m2≥0,
∴不论m为何值,该方程总有两个实数根;
(2)解:把x=2代入方程x2﹣4mx+m2=0得4﹣8m+m2=0,
即:m2﹣8m=﹣4,
∴原式=m2﹣8m+10
=﹣4+10
=6.
21.(1)证明:如图,连接AE.
∵AB是圆O的直径,
∴∠AEB=90°,
即AE⊥BC.
又∵AB=AC,
∴AE是边BC上的中线,
∴BE=CE;
(2)解:∵AB=6,
∴OA=3.
又∵OA=OD,∠BAC=54°,
∴∠AOD=180°﹣2×54°=72°,
∴的长为:=.
22.解:(1)本次调查中一共调查了2÷10%=20名,
∴最喜爱名著阅读的人数为20﹣5﹣6﹣4﹣2=3名,
∴“名著阅读”所占的圆心角度数为,
补全条形统计图如下:
(2)恰好最喜爱的课程是“艺术欣赏”的概率为;
(3),
答:估计全校最喜爱的课程是“体育锻炼”的学生人数为900名.
23.(1)证明:∵△ABC为等边三角形,
∴∠BAC=∠ACB=60°,
∵∠ADB=∠ACB=60°,∠CDB=∠BAC=60°,
∴∠ADB=∠CDB,
∴BD平分∠ADC;
(2)解:在DB截取DE=DC=2,连接CE,如图,
∵∠CDE=60°,DE=DC,
∴△DEC为等边三角形,
∴CE=CD,∠DEC=60°,
∵∠BEC=180°﹣∠DEC=120°,∠ADC=∠ADB+∠CDB=120°,
∴∠BEC=∠ADC,
∵∠CBE和∠CAD都对应,
∴∠CBE=∠CAD,
∵△ABC为等边三角形,
∴BC=CA,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(AAS),
∴BE=AD=3,
∴BD=BE+DE=3+2=5.
24.解:(1)证明:连接OC,
∵AB是直径,
∴∠ACB=∠OCA+∠OCB=90°,
∵OA=OC,∠BCD=∠A,
∴∠OCA=∠A=∠BCD,
∴∠OCD=∠BCD+∠OCB=90°,
∴OC⊥CD,
∵OC是⊙O的半径,
∴直线CD是⊙O的切线;
(2)解:∵∠ACD=120°,∠ACB=90°,
∴∠A=∠BCD=120°﹣90°=30°,
∴∠BOC=∠A+∠OCA=60°,
∵AB=4,
∴OC=2,
在Rt△OCD中,∠D=90°﹣60°=30°,
∴OD=4,
∴,
∴阴影部分的面积=.
25.解:(1)设该品牌图书销量的月平均增长率为x,
根据题意得:3000(1+x)2=4320,
解得:x1=0.2=20%,x2=﹣2.2(不符合题意,舍去),
答:该品牌图书销量的月平均增长率为20%;
(2)设该品牌图书每本降价元m元,则每本的售价应为(40﹣m)元,平均每天的销售量为(100+10m)本,
根据题意得:(40﹣m﹣20)(100+10m)=(40﹣20)×100,
整理得:m2﹣10m=0,
解得:x1=10,x2=0(不符合题意,舍去),
∴40﹣m=30,
答:该品牌图书每本的售价应为30元.
26.(1)证明:连接OD,则OD=OB,
∴∠ODB=∠ABC,
∵AB=AC,
∴∠C=∠ABC,
∴∠ODB=∠C,
∴OD∥AC,
∵DE⊥AC于点E,
∴∠ODE=∠DEC=90°,
∵OD是⊙O的半径,且DE⊥OD,
∴DE是⊙O的切线.
(2)解:连接OE,延长DO交BF于点H,
∵AB是⊙O的直径,
∴∠F=90°,
∵∠HDE=∠DEF=90°,
∴四边形DEFH是矩形,
∴∠DHF=90°,
∵AB=AC,BF=2,FC=10,OH⊥BF,
∴AF=10﹣AC=10﹣AB,DE=FH=BH=BF=,
∵BF2+AF2=AB2,
∴(2)2+(10﹣AB)2=AB2,
解得AB=6,
∴OD=AB=3,
∴OE===,
∴OE的长为.
27.解:(1)连接OD,如图1,
∵BF=DF,
∴∠B=∠BDF,
∵∠C=90°,
∴∠OAD+∠B=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA+∠BDF=90°,
∴∠ODF=90°,
∴DF是半圆O的切线;
(2)连接OF,OD,如图2,
设圆的半径为r,则OD=OE=r,
∵AC=4,BC=3,CF=1,
∴OC=4﹣r,DF=BF=3﹣1=2,
∵OD2+DF2=OF2=OC2+CF2,
∴r2+22=(4﹣r)2+12,
∴r=.
故圆的半径为.
一.选择题(共10小题)
1.一组数据为﹣1,2,3,4,6,6,从这组数据中抽取一个数,抽到的数为6的概率是( )
A. B. C. D.
2.样本数据2、a、3、4的平均数是3,则a的值是( )
A.1 B.2 C.3 D.4
3.下列各方程中,一定是一元二次方程的是( )
A. B.x2+5x﹣3=x(x﹣1) C.(x﹣2)2=2(x﹣2) D.x2+2y=3
4.如图,四边形ABCD外切于⊙O,且AB=10,CD=15,则四边形ABCD的周长为( )
A.60 B.55 C.45 D.50
5.用半径为60,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面半径是( )
A.10 B.20 C.30 D.40
6.若关于x的一元二次方程kx2﹣6x+3=0有两个不相等的实数根,则k的取值范围是( )
A.k>3 B.k≠0 C.k<3 D.k<3且k≠0
7.如图,CD是⊙O的直径,若AB⊥CD,垂足为B,∠OAB=40°,则∠C的度数为( )
A.25° B.20° C.10° D.30°
8.若x1,x2是方程5x2+x﹣5=0的两个根,则的值为( )
A.﹣1 B. C.5 D.
9.如图,圆锥的侧面展开图是一个圆心角为72°的扇形,若扇形的半径l是5,则该圆锥的体积是( )
A.π B.π C.2π D.π
10.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,与BC相交于点G,则下列结论:①∠BAD=∠CAD;②若∠BAC=50°,则∠BEC=130°;③若点G为BC的中点,则∠BGD=90°;④BD=DE.其中一定正确的个数是( )
A.1 B.2 C.3 D.4
二.填空题(共8小题)
11.一个不透明的盒子里有形状、大小相同的黄球2个、红球3个,从盒子里任意摸出1个球,摸到红球的概率是 .
12.若一组数据a1,a2,…,an的平均数为4,方差为3,那么数据2a1+3,2a2+3,…,2an+3的平均数和方差分别是 , .
13.已知关于x的方程(m+1)x|4m|﹣2+27mx+5=0是一元二次方程,则m= .
14.同一平面内,⊙O内一点P到圆上的最大距离为6cm,最小距离为2cm,则⊙O的半径为 cm.
15.如图,AB是⊙O的弦,半径OD⊥AB于点C,AE为直径,AB=8,CD=2,则线段CE的长为 .
16.某文具店为迎接“购物节”,提高水笔销量,经过两次降价后(每次降价的百分率相同),由每盒25元降至每盒16元.则降价的百分率为 .
17.如图,△ABC为⊙O的内接三角形,O为圆心,OD⊥AB于点D,OE⊥AC于点E,若DE=5,则BC= .
18.如图,在矩形ABCD中,AB=6,BC=4,P是矩形内部一动点,且满足∠BCP=∠PDC,则线段BP的最小值是 ;当BP取最小值时,DP延长线交线段BC于E,则CE的长为 .
三.解答题(共9小题)
19.解方程:
(1)x2﹣6x+5=0. (2)2x2+3x﹣5=0.
20.已知关于x的一元二次方程x2﹣4mx+m2=0.
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若x=2是该方程的根,求代数式(m﹣2)2﹣2(2m﹣3)的值.
21.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.
(1)求证:BE=CE;
(2)若AB=6,∠BAC=54°,求劣弧的长.
22.2022年底新冠病毒爆发,学校进行在线教学.小杰同学为了了解网课学习情况,对本班部分同学最喜爱的课程进行了调查,课程分别是网上授课、体育锻炼、名著阅读、艺术欣赏和其他课程,并制成以下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)本次调查中一共调查了 名学生,其中“名著阅读”所占的圆心角度数为 °,并把条形统计图补全.
(2)在调查的同学中随机选取一名学生,求他恰好最喜爱的课程是“艺术欣赏”的概率.
(3)若该校一共有3000名学生,请估算出全校最喜爱的课程是“体育锻炼”的人数.
23.如图所示,等边△ABC内接于⊙O,D为圆周上一点.
(1)求证:BD平分∠ADC;
(2)若CD=2,AD=3,求BD的长度.
24.如图,AB是⊙O直径,点C在⊙O上,在AB的延长线上取一点D,连接CD,使∠BCD=∠A.
(1)求证:直线CD是⊙O的切线;
(2)若∠ACD=120°,AB=4,求图中阴影部分的面积.
25.为鼓励和推广全民阅读,某品牌图书开展了促销活动.八月份售出图书3000本,十月份售出图书4320本.
(1)求该品牌图书销量的月平均增长率;
(2)该品牌图书每本成本为20元,当售价为40元/本时,平均每天的销售量为100本.经试销统计发现,如果该品牌图书的售价每降价1元,那么平均每天可多售出10本.若要使平均每天的利润保持不变,并且让消费者尽可能获得实惠,那么该品牌图书每本的售价应为多少元?
26.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,垂足为点E,延长CA交⊙O于点F,连接BF.
(1)求证:DE是⊙O的切线;
(2)连接OE,若BF=,FC=10,求OE的长.
27.如图,在Rt△ABC中,∠C=90°,点O在AC上,以OA为半径的半圆O交AB于点D,交AC于点E,点F在BC上,且BF=DF.
(1)求证:DF是半圆O的切线;
(2)若AC=4,BC=3,CF=1,求半圆O的半径长.
参考答案
一.选择题(共10小题)
1.A.
2.C.
3.C.
4.D.
5.B.
6.D.
7.A.
8.D.
9.D.
10.C.
二.填空题(共8小题)
11..
12.11,12.
13.1.
14.4.
15.2.
16.20%.
17.10.
18.2;3.
三.解答题(共9小题)
19.解:(1)x2﹣6x+5=0,
(x﹣1)(x﹣5)=0,
x﹣1=0或x﹣5=0,
∴x1=1,x2=5;
(2)2x2+3x﹣5=0,
(2x+5)(x﹣1)=0,
2x+5=0或x﹣1=0,
∴,x2=1.
20.(1)证明:∵x2﹣4mx+m2=0,
∴a=1,b=﹣4m,c=m2,
∴Δ=(﹣4m)2﹣4m2=12m2≥0,
∴不论m为何值,该方程总有两个实数根;
(2)解:把x=2代入方程x2﹣4mx+m2=0得4﹣8m+m2=0,
即:m2﹣8m=﹣4,
∴原式=m2﹣8m+10
=﹣4+10
=6.
21.(1)证明:如图,连接AE.
∵AB是圆O的直径,
∴∠AEB=90°,
即AE⊥BC.
又∵AB=AC,
∴AE是边BC上的中线,
∴BE=CE;
(2)解:∵AB=6,
∴OA=3.
又∵OA=OD,∠BAC=54°,
∴∠AOD=180°﹣2×54°=72°,
∴的长为:=.
22.解:(1)本次调查中一共调查了2÷10%=20名,
∴最喜爱名著阅读的人数为20﹣5﹣6﹣4﹣2=3名,
∴“名著阅读”所占的圆心角度数为,
补全条形统计图如下:
(2)恰好最喜爱的课程是“艺术欣赏”的概率为;
(3),
答:估计全校最喜爱的课程是“体育锻炼”的学生人数为900名.
23.(1)证明:∵△ABC为等边三角形,
∴∠BAC=∠ACB=60°,
∵∠ADB=∠ACB=60°,∠CDB=∠BAC=60°,
∴∠ADB=∠CDB,
∴BD平分∠ADC;
(2)解:在DB截取DE=DC=2,连接CE,如图,
∵∠CDE=60°,DE=DC,
∴△DEC为等边三角形,
∴CE=CD,∠DEC=60°,
∵∠BEC=180°﹣∠DEC=120°,∠ADC=∠ADB+∠CDB=120°,
∴∠BEC=∠ADC,
∵∠CBE和∠CAD都对应,
∴∠CBE=∠CAD,
∵△ABC为等边三角形,
∴BC=CA,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(AAS),
∴BE=AD=3,
∴BD=BE+DE=3+2=5.
24.解:(1)证明:连接OC,
∵AB是直径,
∴∠ACB=∠OCA+∠OCB=90°,
∵OA=OC,∠BCD=∠A,
∴∠OCA=∠A=∠BCD,
∴∠OCD=∠BCD+∠OCB=90°,
∴OC⊥CD,
∵OC是⊙O的半径,
∴直线CD是⊙O的切线;
(2)解:∵∠ACD=120°,∠ACB=90°,
∴∠A=∠BCD=120°﹣90°=30°,
∴∠BOC=∠A+∠OCA=60°,
∵AB=4,
∴OC=2,
在Rt△OCD中,∠D=90°﹣60°=30°,
∴OD=4,
∴,
∴阴影部分的面积=.
25.解:(1)设该品牌图书销量的月平均增长率为x,
根据题意得:3000(1+x)2=4320,
解得:x1=0.2=20%,x2=﹣2.2(不符合题意,舍去),
答:该品牌图书销量的月平均增长率为20%;
(2)设该品牌图书每本降价元m元,则每本的售价应为(40﹣m)元,平均每天的销售量为(100+10m)本,
根据题意得:(40﹣m﹣20)(100+10m)=(40﹣20)×100,
整理得:m2﹣10m=0,
解得:x1=10,x2=0(不符合题意,舍去),
∴40﹣m=30,
答:该品牌图书每本的售价应为30元.
26.(1)证明:连接OD,则OD=OB,
∴∠ODB=∠ABC,
∵AB=AC,
∴∠C=∠ABC,
∴∠ODB=∠C,
∴OD∥AC,
∵DE⊥AC于点E,
∴∠ODE=∠DEC=90°,
∵OD是⊙O的半径,且DE⊥OD,
∴DE是⊙O的切线.
(2)解:连接OE,延长DO交BF于点H,
∵AB是⊙O的直径,
∴∠F=90°,
∵∠HDE=∠DEF=90°,
∴四边形DEFH是矩形,
∴∠DHF=90°,
∵AB=AC,BF=2,FC=10,OH⊥BF,
∴AF=10﹣AC=10﹣AB,DE=FH=BH=BF=,
∵BF2+AF2=AB2,
∴(2)2+(10﹣AB)2=AB2,
解得AB=6,
∴OD=AB=3,
∴OE===,
∴OE的长为.
27.解:(1)连接OD,如图1,
∵BF=DF,
∴∠B=∠BDF,
∵∠C=90°,
∴∠OAD+∠B=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA+∠BDF=90°,
∴∠ODF=90°,
∴DF是半圆O的切线;
(2)连接OF,OD,如图2,
设圆的半径为r,则OD=OE=r,
∵AC=4,BC=3,CF=1,
∴OC=4﹣r,DF=BF=3﹣1=2,
∵OD2+DF2=OF2=OC2+CF2,
∴r2+22=(4﹣r)2+12,
∴r=.
故圆的半径为.
同课章节目录
