第三章 分式 综合练习(含答案)2024—2025学年青岛版数学八年级上册
文档属性
| 名称 | 第三章 分式 综合练习(含答案)2024—2025学年青岛版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 140.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 00:00:00 | ||
图片预览


文档简介
第三章综合练习
1.填空:
(1) 当分式 的值为0时,x的值是 ;
(2)已知1,2,3三个数,请你添加一个数,写出一个比例式 。
2. 选择题:太阳能热水器安装有一个进水管(冷水管)和一个出水管(热水管)。单独打开进水管,xh可以将空的热水器注满水;单独打开出水管,yh可以把注满水的热水器中的水放尽(x(A)y-x
3. x为何值时,下列分式有意义
如果把分式 中的x和y都扩大到原来的3倍,分式的值有没有变化 为什么
5.计算下列各式:
6.计算:
小亮收集生物标本的件数是大刚的 ,大刚收集标本的件数是小莹的 小亮、大刚、小莹三人收集标本的件数的比是多少
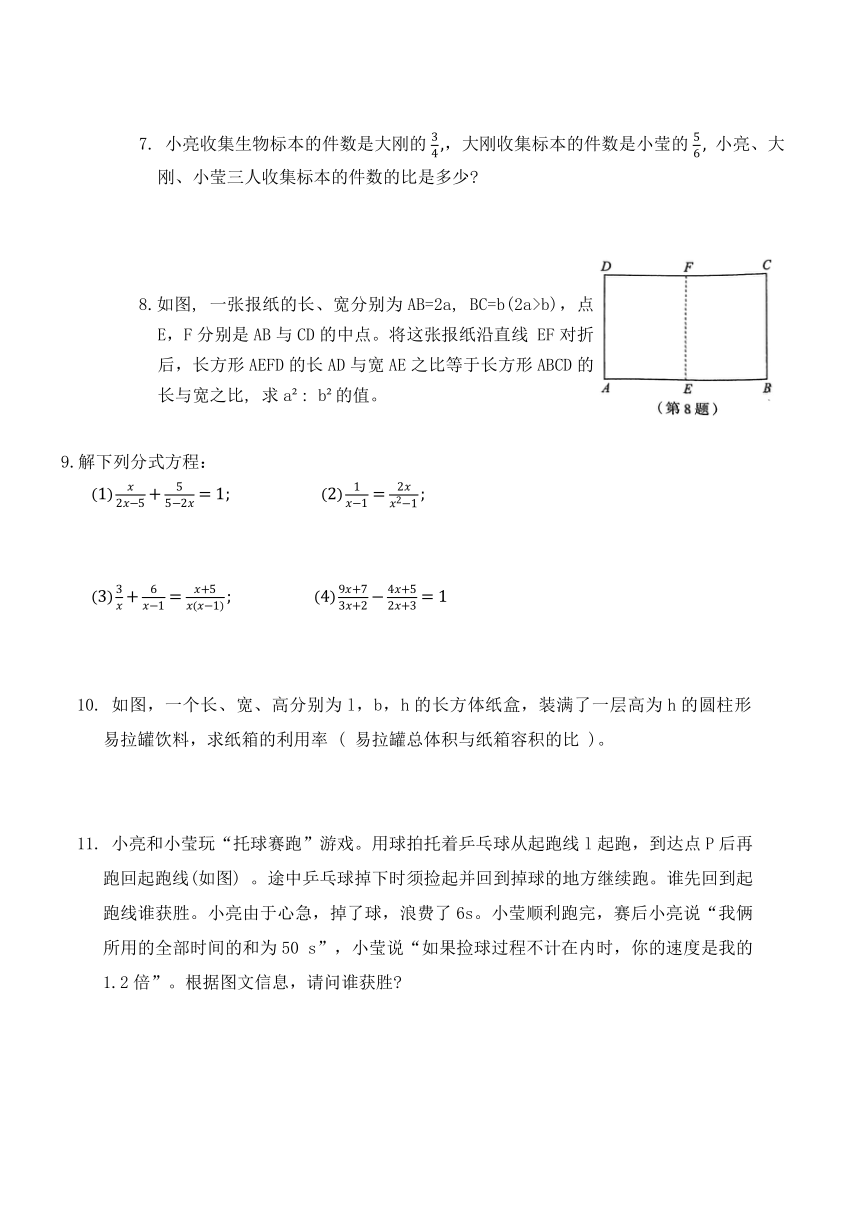
8.如图, 一张报纸的长、宽分别为AB=2a, BC=b(2a>b),点E,F分别是AB与CD的中点。将这张报纸沿直线 EF对折后,长方形AEFD的长AD与宽AE之比等于长方形ABCD的长与宽之比, 求a : b 的值。
9.解下列分式方程:
如图,一个长、宽、高分别为l,b,h的长方体纸盒,装满了一层高为h的圆柱形易拉罐饮料,求纸箱的利用率 ( 易拉罐总体积与纸箱容积的比 )。
11. 小亮和小莹玩“托球赛跑”游戏。用球拍托着乒乓球从起跑线l起跑,到达点P后再跑回起跑线(如图) 。途中乒乓球掉下时须捡起并回到掉球的地方继续跑。谁先回到起跑线谁获胜。小亮由于心急,掉了球,浪费了6s。小莹顺利跑完,赛后小亮说“我俩所用的全部时间的和为50 s”,小莹说“如果捡球过程不计在内时,你的速度是我的1.2倍”。根据图文信息,请问谁获胜
(1) 已知 求 的值;
(2)已知 求 的值。
A地至B地的铁路里程为650km。从A地乘“G”字头列车和“D”字头列车都可直达B地。已知“G”字头列车的时速为“D”字头列车时速的2倍,且运行时间比“D”字头列车少2.5h,求“G”字头列车从A至B的运行时间及时速。
“公共交通优先”是践行绿色出行的重要方式。为响应市政府倡议,某公司员工小王上班由自驾车改为乘坐公交车。已知小王家距上班地点18km,他乘公交车平均每小时行驶的路程比他自驾车平均每小时行驶的路程的2倍还多9km。他从家出发到上班地点,乘公交车所用的时间是自驾车所用时间的 。小王用自驾车上班平均每小时行驶多少千米
已知关于x的方程 有增根,求a的值。
16.已知x为整数,且 的结果也为整数,求所有符合条件的x的值。
参考答案:
1(1)3
(2)(答案不唯一) 1:2=3:6
2D
3解:(1)当x+1≠0,即x≠-1时,分式 有意义;(2)当1-2x≠0,即 时,分式 有意义.
4解:分式的值没有变化.理由:因为当x和y都扩大到原来的3倍时, 所以分式的值不变.
5 解:
6解:
=x-y.
7解:方法一 由题意知,小亮收集的生物标本件数:大刚收集的生物标本件数=3:4,大刚收集的生物标本件数:小莹收集的生物标本件数=5:6,也即小亮收集的生物标本件数:大刚收集的生物标本件数=15:20,大刚收集的生物标本件数:小莹收集的生物标本件数=20:24,所以小亮收集的生物标本件数:大刚收集的生物标本件数:小莹收集的生物标本件数=15:20:24,所以小亮、大刚、小莹三人收集标本的件数比为15:20:24.
方法二 设小莹收集标本x件,则大刚收集标本 件,小亮收集标本 件,即 件,所以小亮、大刚、小莹三人收集标本的件数的比为
方法三 设大刚收集标本x件,则小亮收集标本 x件,小莹收集标本 x件,所以小亮、大刚、小莹收集标本的件数的比为
8解:由题意,得 即 所以 2a ,所以 所以a :b 的值是
9 解: 整理,得 方程两边都乘(2x-5),得:x -5 =2x-5,解得x=0.经检验,x=0是原方程的根.
方程两边都乘(x+1)(x-1),得x+1=2x,解得x=1.经检验,x=1是原分式方程的增根,所以原方程无解.
方程两边都乘x(x-1),得3(x-1)+6x=x+5,解得x=1.经检验,x=1是原分式方程的增根,所以原方程无解.
方程两边都乘(3x+2)·(2x+3),得(9x+7)(2x+3)-(4x+5)(3x+2)=(3x+2)(2x+3),解得x=-1.经检验,x=-1是原方程的根.
10解:设易拉罐底面半径为r,则易拉罐个数为 所以易拉罐的总体积为 因为长方体纸箱的体积为 lbh,所以纸箱的利用率为
答:纸箱的利用率为π/4.
11 解:设小莹的速度为 xm/s,则小亮的速度为1.2xm/s.
根据题意,得 解得x=2.5.经检验,x=2.5是分式方程的根,且符合题意.所以1.2x=3.
小莹回到起点的时间为60÷2.5 =24(s).
小亮回到起点的时间为60÷3+6=26(s).
因为24<26,所以小莹先回到起点,故小莹获胜.
12解: 所以
所以 所以
(2)设
则x=2k,y-z=3k,z+x=5k,所以z=3k,y=6k,所以
13解:设“D”字头列车的时速为 x km/h,则“G”字头列车的时速为2x km/h.根据题意,得
解得x=130.经检验,x=130 是分式方程的根,且符合题意.
所以从A 到B 的运行时间为650÷260=2.5(h).答:“G”字头列车从 A 至 B 的运行时间和时速分别为2.5 h和260 km/h.
14解:设小王用自驾车上班平均每小时行驶 xkm,则乘公交车上班平均每小时行驶(2x+9) km.根据题意,得 解得x=27.经检验,x=27是分式方程的根,且符合题意,所以小王用自驾车上班平均每小时行驶27 km.
15解:因为分式方程有增根,所以x-1=0.所以x=1是分式方程的增根.
去分母,得 ax+1-(x-1) =0.把x=1代入,得a=-1.
所以当分式方程有增根时,a的值为-1.
16解:
要使 为整数且x为整数,则x-3=±1或±2,所以x=4或x=2或x=5或x=1,所以符合条件的x的值为1,2,4,5.
1.填空:
(1) 当分式 的值为0时,x的值是 ;
(2)已知1,2,3三个数,请你添加一个数,写出一个比例式 。
2. 选择题:太阳能热水器安装有一个进水管(冷水管)和一个出水管(热水管)。单独打开进水管,xh可以将空的热水器注满水;单独打开出水管,yh可以把注满水的热水器中的水放尽(x
3. x为何值时,下列分式有意义
如果把分式 中的x和y都扩大到原来的3倍,分式的值有没有变化 为什么
5.计算下列各式:
6.计算:
小亮收集生物标本的件数是大刚的 ,大刚收集标本的件数是小莹的 小亮、大刚、小莹三人收集标本的件数的比是多少
8.如图, 一张报纸的长、宽分别为AB=2a, BC=b(2a>b),点E,F分别是AB与CD的中点。将这张报纸沿直线 EF对折后,长方形AEFD的长AD与宽AE之比等于长方形ABCD的长与宽之比, 求a : b 的值。
9.解下列分式方程:
如图,一个长、宽、高分别为l,b,h的长方体纸盒,装满了一层高为h的圆柱形易拉罐饮料,求纸箱的利用率 ( 易拉罐总体积与纸箱容积的比 )。
11. 小亮和小莹玩“托球赛跑”游戏。用球拍托着乒乓球从起跑线l起跑,到达点P后再跑回起跑线(如图) 。途中乒乓球掉下时须捡起并回到掉球的地方继续跑。谁先回到起跑线谁获胜。小亮由于心急,掉了球,浪费了6s。小莹顺利跑完,赛后小亮说“我俩所用的全部时间的和为50 s”,小莹说“如果捡球过程不计在内时,你的速度是我的1.2倍”。根据图文信息,请问谁获胜
(1) 已知 求 的值;
(2)已知 求 的值。
A地至B地的铁路里程为650km。从A地乘“G”字头列车和“D”字头列车都可直达B地。已知“G”字头列车的时速为“D”字头列车时速的2倍,且运行时间比“D”字头列车少2.5h,求“G”字头列车从A至B的运行时间及时速。
“公共交通优先”是践行绿色出行的重要方式。为响应市政府倡议,某公司员工小王上班由自驾车改为乘坐公交车。已知小王家距上班地点18km,他乘公交车平均每小时行驶的路程比他自驾车平均每小时行驶的路程的2倍还多9km。他从家出发到上班地点,乘公交车所用的时间是自驾车所用时间的 。小王用自驾车上班平均每小时行驶多少千米
已知关于x的方程 有增根,求a的值。
16.已知x为整数,且 的结果也为整数,求所有符合条件的x的值。
参考答案:
1(1)3
(2)(答案不唯一) 1:2=3:6
2D
3解:(1)当x+1≠0,即x≠-1时,分式 有意义;(2)当1-2x≠0,即 时,分式 有意义.
4解:分式的值没有变化.理由:因为当x和y都扩大到原来的3倍时, 所以分式的值不变.
5 解:
6解:
=x-y.
7解:方法一 由题意知,小亮收集的生物标本件数:大刚收集的生物标本件数=3:4,大刚收集的生物标本件数:小莹收集的生物标本件数=5:6,也即小亮收集的生物标本件数:大刚收集的生物标本件数=15:20,大刚收集的生物标本件数:小莹收集的生物标本件数=20:24,所以小亮收集的生物标本件数:大刚收集的生物标本件数:小莹收集的生物标本件数=15:20:24,所以小亮、大刚、小莹三人收集标本的件数比为15:20:24.
方法二 设小莹收集标本x件,则大刚收集标本 件,小亮收集标本 件,即 件,所以小亮、大刚、小莹三人收集标本的件数的比为
方法三 设大刚收集标本x件,则小亮收集标本 x件,小莹收集标本 x件,所以小亮、大刚、小莹收集标本的件数的比为
8解:由题意,得 即 所以 2a ,所以 所以a :b 的值是
9 解: 整理,得 方程两边都乘(2x-5),得:x -5 =2x-5,解得x=0.经检验,x=0是原方程的根.
方程两边都乘(x+1)(x-1),得x+1=2x,解得x=1.经检验,x=1是原分式方程的增根,所以原方程无解.
方程两边都乘x(x-1),得3(x-1)+6x=x+5,解得x=1.经检验,x=1是原分式方程的增根,所以原方程无解.
方程两边都乘(3x+2)·(2x+3),得(9x+7)(2x+3)-(4x+5)(3x+2)=(3x+2)(2x+3),解得x=-1.经检验,x=-1是原方程的根.
10解:设易拉罐底面半径为r,则易拉罐个数为 所以易拉罐的总体积为 因为长方体纸箱的体积为 lbh,所以纸箱的利用率为
答:纸箱的利用率为π/4.
11 解:设小莹的速度为 xm/s,则小亮的速度为1.2xm/s.
根据题意,得 解得x=2.5.经检验,x=2.5是分式方程的根,且符合题意.所以1.2x=3.
小莹回到起点的时间为60÷2.5 =24(s).
小亮回到起点的时间为60÷3+6=26(s).
因为24<26,所以小莹先回到起点,故小莹获胜.
12解: 所以
所以 所以
(2)设
则x=2k,y-z=3k,z+x=5k,所以z=3k,y=6k,所以
13解:设“D”字头列车的时速为 x km/h,则“G”字头列车的时速为2x km/h.根据题意,得
解得x=130.经检验,x=130 是分式方程的根,且符合题意.
所以从A 到B 的运行时间为650÷260=2.5(h).答:“G”字头列车从 A 至 B 的运行时间和时速分别为2.5 h和260 km/h.
14解:设小王用自驾车上班平均每小时行驶 xkm,则乘公交车上班平均每小时行驶(2x+9) km.根据题意,得 解得x=27.经检验,x=27是分式方程的根,且符合题意,所以小王用自驾车上班平均每小时行驶27 km.
15解:因为分式方程有增根,所以x-1=0.所以x=1是分式方程的增根.
去分母,得 ax+1-(x-1) =0.把x=1代入,得a=-1.
所以当分式方程有增根时,a的值为-1.
16解:
要使 为整数且x为整数,则x-3=±1或±2,所以x=4或x=2或x=5或x=1,所以符合条件的x的值为1,2,4,5.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
