第十二章 全等三角形 单元测试(含答案)2024-2025学年人教版八年级上册数学
文档属性
| 名称 | 第十二章 全等三角形 单元测试(含答案)2024-2025学年人教版八年级上册数学 |  | |
| 格式 | docx | ||
| 文件大小 | 530.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 10:26:55 | ||
图片预览

文档简介
第十二章全等三角形(单元测试)2024-2025学年八年级上册数学人教版
一、单选题
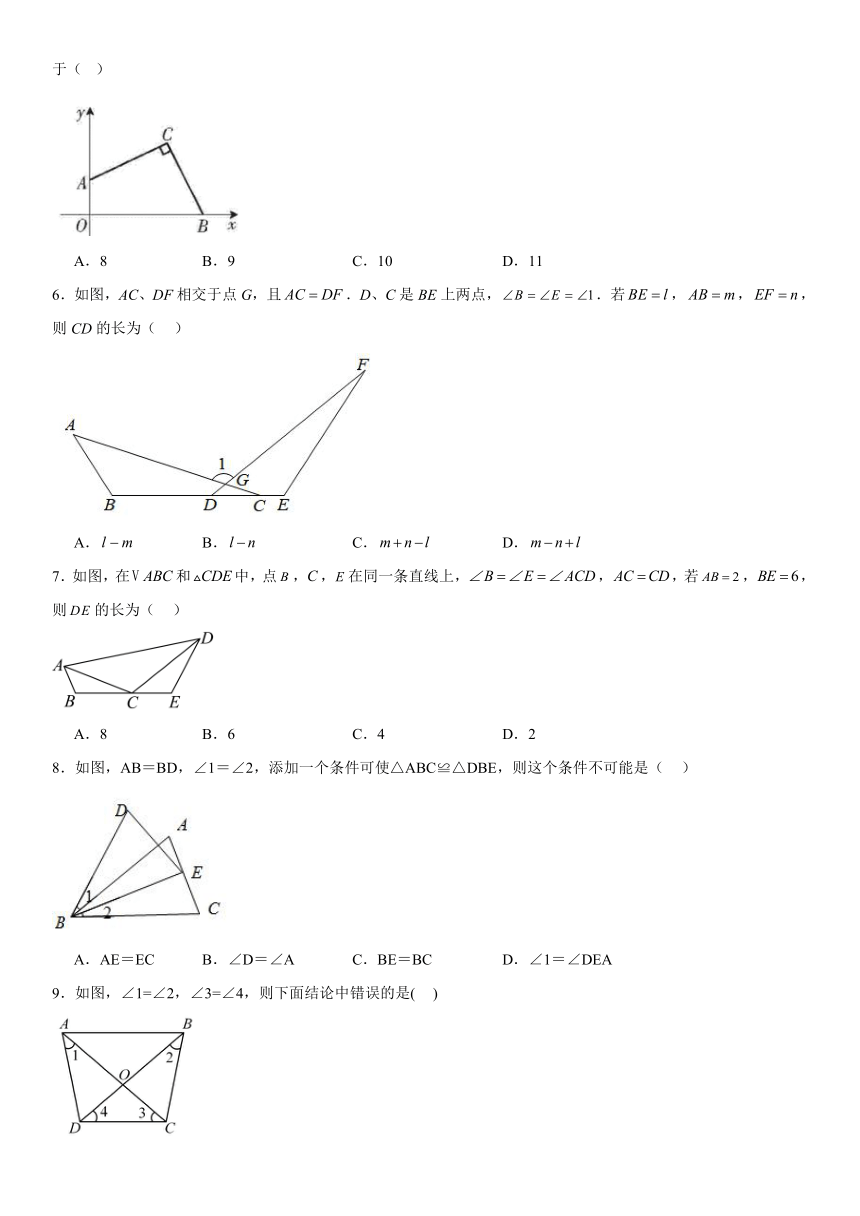
1.如图,点在同一条直线上,已知,,添加下列条件中的一个,能使的是( )
A. B. C. D.
2.如图,在中,,点O是、的平分线的交点,且,,则点O到边的距离为( )
A. B. C. D.
3.如图,,,要根据“”说明,则还需要添加的一个条件是( )
A. B. C. D.
4.如图,在中,,,若,,则点的坐标为( )
A. B. C. D.
5.如图,在平面直角坐标系中,点,点分别在轴正半轴和轴正半轴上,,则等于( )
A.8 B.9 C.10 D.11
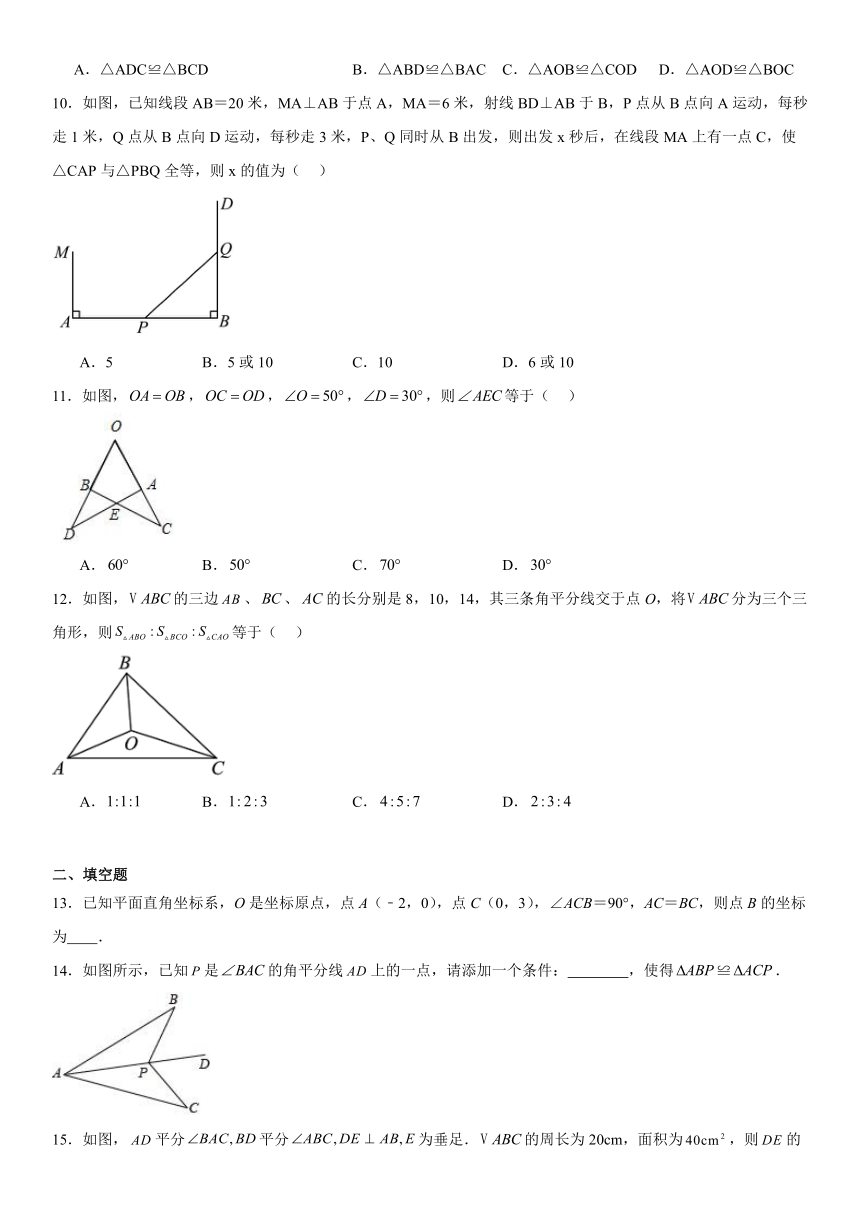
6.如图,AC、DF相交于点G,且.D、C是BE上两点,.若,,,则CD的长为( )
A. B. C. D.
7.如图,在和中,点,,在同一条直线上,,,若,,则的长为( )
A.8 B.6 C.4 D.2
8.如图,AB=BD,∠1=∠2,添加一个条件可使△ABC≌△DBE,则这个条件不可能是( )
A.AE=EC B.∠D=∠A C.BE=BC D.∠1=∠DEA
9.如图,∠1=∠2,∠3=∠4,则下面结论中错误的是( )
A.△ADC≌△BCD B.△ABD≌△BAC C.△AOB≌△COD D.△AOD≌△BOC
10.如图,已知线段AB=20米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A.5 B.5或10 C.10 D.6或10
11.如图,,,,,则等于( )
A. B. C. D.
12.如图,的三边、、的长分别是8,10,14,其三条角平分线交于点O,将分为三个三角形,则等于( )
A. B. C. D.
二、填空题
13.已知平面直角坐标系,O是坐标原点,点A(﹣2,0),点C(0,3),∠ACB=90°,AC=BC,则点B的坐标为 .
14.如图所示,已知是的角平分线上的一点,请添加一个条件: ,使得.
15.如图,平分平分为垂足.的周长为20cm,面积为,则的长为 .
16.如图,在平面直角坐标系中,将直角三角形的直角顶点放在点P(4,4)处,两直角边分别与坐标轴交于点A和点B,则OA+OB的值为 .
17.如图, 是的角平分线,于 E ,若 , ,的面积等于 15 ,则 .
18.如图,中,,平分,若,则点D到线段的距离等于 .
19.如图,点P,Q是直线y=﹣上的两点,P在Q的左侧,且满足OP=OQ,OP⊥OQ,则点P的坐标是 .
20.如图,在四边形ABCD中,连接BD,∠A=90°,AD=6,∠ABD=∠CBD.若BC=13,则S△DBC= .
三、解答题
21.(1)课本习题回放:
“如图①,,,,,垂足分别为D,E,,.求的长”.请直接写出此题答案:的长为_______cm.
(2)探索证明:
如图②,点B,C在的边、上,,点E,F在内部的射线上,且.求证:.
(3)拓展应用:
如图③,在中,,.点D在边上,点E在线段上,.若,则_______.(图中画出分析思路;直接填写结果)
22.政府准备在如图所示的河流上方修建一座桥梁方便河流两岸的人们通行交流,现需测量此段河流的宽度(该段河流两岸是平行的),工作人员是这样做的:先在河流的一条岸边E点,选对岸正对的一棵树A为参照点(即),再沿河岸直走有一棵树C,继续前行到达D处,从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走,测得的长为,求河流的宽度.
23.如图△ABC中,AD平分∠BAC,AB=4,AC=2,且△ABD的面积为3,求△ACD的面积.
24.如图,长方形纸片的边,对角线是边上的一个动点,如图,沿翻折纸片,点落在点处,易得,连接.
图1 图2
(1)猜想与之间的数量关系,并说明理由.
(2)线段的长是否存在最小值 小贤与同学探讨后发现:,可先连接,然后再运用相关知识求解,请你根据小贤的思路继续思考,并写出解答过程.
参考答案:
1.B
2.B
3.A
4.D
5.A
6.C
7.C
8.A
9.C
10.A
11.C
12.C
13.(-3,5)或(3,1)/(3,1)或(-3,5)
14.(答案不唯一)
15.4cm
16.8
17.2
18.2.
19..
20.
21.(1);(2)略;(3)
22.河流的宽度的长是
23.1.5
24.(1)
(2)有最小值为.
一、单选题
1.如图,点在同一条直线上,已知,,添加下列条件中的一个,能使的是( )
A. B. C. D.
2.如图,在中,,点O是、的平分线的交点,且,,则点O到边的距离为( )
A. B. C. D.
3.如图,,,要根据“”说明,则还需要添加的一个条件是( )
A. B. C. D.
4.如图,在中,,,若,,则点的坐标为( )
A. B. C. D.
5.如图,在平面直角坐标系中,点,点分别在轴正半轴和轴正半轴上,,则等于( )
A.8 B.9 C.10 D.11
6.如图,AC、DF相交于点G,且.D、C是BE上两点,.若,,,则CD的长为( )
A. B. C. D.
7.如图,在和中,点,,在同一条直线上,,,若,,则的长为( )
A.8 B.6 C.4 D.2
8.如图,AB=BD,∠1=∠2,添加一个条件可使△ABC≌△DBE,则这个条件不可能是( )
A.AE=EC B.∠D=∠A C.BE=BC D.∠1=∠DEA
9.如图,∠1=∠2,∠3=∠4,则下面结论中错误的是( )
A.△ADC≌△BCD B.△ABD≌△BAC C.△AOB≌△COD D.△AOD≌△BOC
10.如图,已知线段AB=20米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A.5 B.5或10 C.10 D.6或10
11.如图,,,,,则等于( )
A. B. C. D.
12.如图,的三边、、的长分别是8,10,14,其三条角平分线交于点O,将分为三个三角形,则等于( )
A. B. C. D.
二、填空题
13.已知平面直角坐标系,O是坐标原点,点A(﹣2,0),点C(0,3),∠ACB=90°,AC=BC,则点B的坐标为 .
14.如图所示,已知是的角平分线上的一点,请添加一个条件: ,使得.
15.如图,平分平分为垂足.的周长为20cm,面积为,则的长为 .
16.如图,在平面直角坐标系中,将直角三角形的直角顶点放在点P(4,4)处,两直角边分别与坐标轴交于点A和点B,则OA+OB的值为 .
17.如图, 是的角平分线,于 E ,若 , ,的面积等于 15 ,则 .
18.如图,中,,平分,若,则点D到线段的距离等于 .
19.如图,点P,Q是直线y=﹣上的两点,P在Q的左侧,且满足OP=OQ,OP⊥OQ,则点P的坐标是 .
20.如图,在四边形ABCD中,连接BD,∠A=90°,AD=6,∠ABD=∠CBD.若BC=13,则S△DBC= .
三、解答题
21.(1)课本习题回放:
“如图①,,,,,垂足分别为D,E,,.求的长”.请直接写出此题答案:的长为_______cm.
(2)探索证明:
如图②,点B,C在的边、上,,点E,F在内部的射线上,且.求证:.
(3)拓展应用:
如图③,在中,,.点D在边上,点E在线段上,.若,则_______.(图中画出分析思路;直接填写结果)
22.政府准备在如图所示的河流上方修建一座桥梁方便河流两岸的人们通行交流,现需测量此段河流的宽度(该段河流两岸是平行的),工作人员是这样做的:先在河流的一条岸边E点,选对岸正对的一棵树A为参照点(即),再沿河岸直走有一棵树C,继续前行到达D处,从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走,测得的长为,求河流的宽度.
23.如图△ABC中,AD平分∠BAC,AB=4,AC=2,且△ABD的面积为3,求△ACD的面积.
24.如图,长方形纸片的边,对角线是边上的一个动点,如图,沿翻折纸片,点落在点处,易得,连接.
图1 图2
(1)猜想与之间的数量关系,并说明理由.
(2)线段的长是否存在最小值 小贤与同学探讨后发现:,可先连接,然后再运用相关知识求解,请你根据小贤的思路继续思考,并写出解答过程.
参考答案:
1.B
2.B
3.A
4.D
5.A
6.C
7.C
8.A
9.C
10.A
11.C
12.C
13.(-3,5)或(3,1)/(3,1)或(-3,5)
14.(答案不唯一)
15.4cm
16.8
17.2
18.2.
19..
20.
21.(1);(2)略;(3)
22.河流的宽度的长是
23.1.5
24.(1)
(2)有最小值为.
