华师大版数学八年级下册 期末综合测试卷(一)(含答案)
文档属性
| 名称 | 华师大版数学八年级下册 期末综合测试卷(一)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 22:52:48 | ||
图片预览



文档简介
期末综合测试卷(一)
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
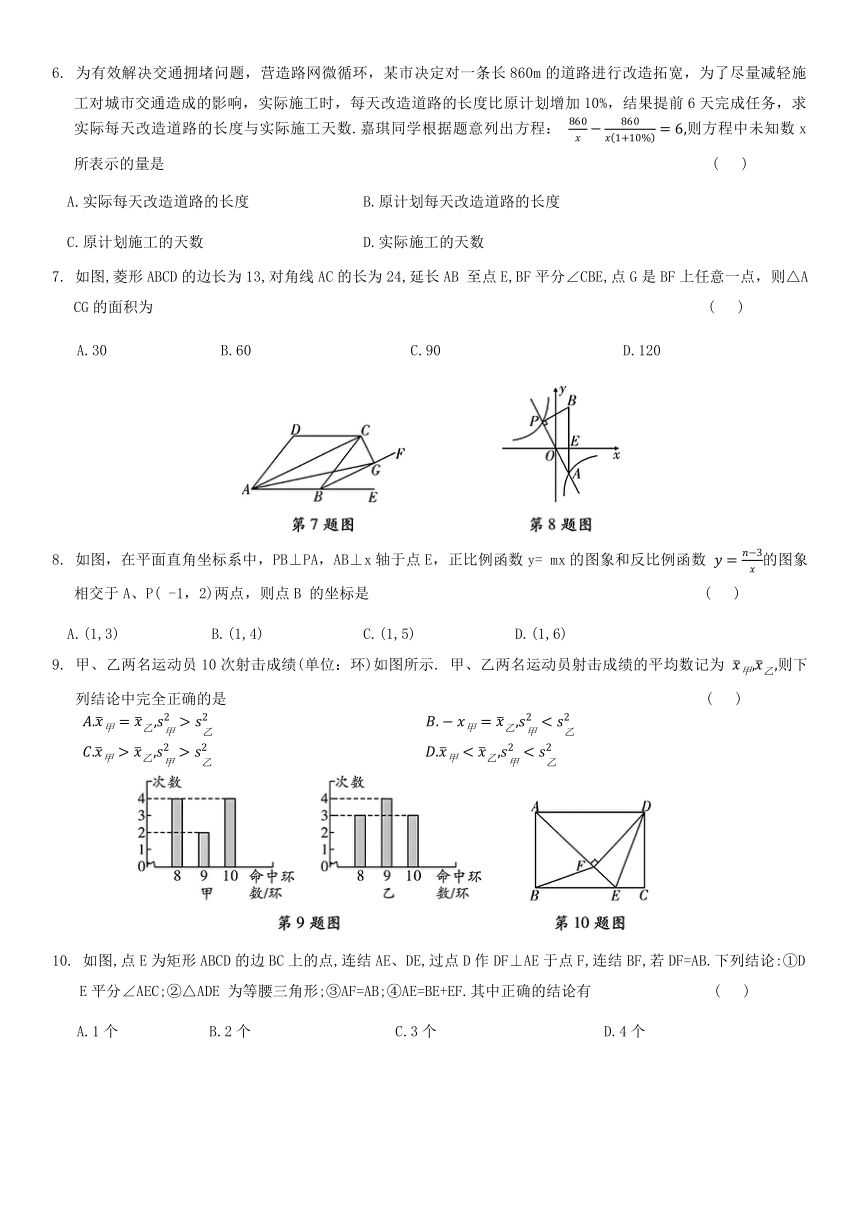
1. 在下列给出的条件中,能判定四边形 ABCD 为平行四边形的是 ( )
A. AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C. AB∥CD,AB=CD D. AB=AD,CB=CD
2. 分式 化简后的结果为 ( )
3. 某校九年级(1)班部分学生上学路上所花的时间如图所示.设他们上学路上所花时间的平均数为a,中位数为b,众数为c,则有 ( )
A. b>a>c
B. c>a>b
C. a>b>c
D. b>c>a
4. 在同一直角坐标系中,一次函数y= kx+b和y= bx+k的图象可能是 ( )
5. 如图,点E在正方形ABCD 的边 CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点 G.若BG=3,CG=2,则CE的长为 ( )
C.4
6. 为有效解决交通拥堵问题,营造路网微循环,某市决定对一条长860m的道路进行改造拓宽,为了尽量减轻施工对城市交通造成的影响,实际施工时,每天改造道路的长度比原计划增加10%,结果提前6天完成任务,求实际每天改造道路的长度与实际施工天数.嘉琪同学根据题意列出方程: 则方程中未知数x所表示的量是 ( )
A.实际每天改造道路的长度 B.原计划每天改造道路的长度
C.原计划施工的天数 D.实际施工的天数
7. 如图,菱形ABCD的边长为13,对角线AC的长为24,延长AB 至点E,BF平分∠CBE,点G是BF上任意一点,则△ACG的面积为 ( )
A.30 B.60 C.90 D.120
8. 如图,在平面直角坐标系中,PB⊥PA,AB⊥x轴于点E,正比例函数y= mx的图象和反比例函数 的图象相交于A、P( -1,2)两点,则点B 的坐标是 ( )
A.(1,3) B.(1,4) C.(1,5) D.(1,6)
9. 甲、乙两名运动员10次射击成绩(单位:环)如图所示. 甲、乙两名运动员射击成绩的平均数记为 则下列结论中完全正确的是 ( )
10. 如图,点E为矩形ABCD的边BC上的点,连结AE、DE,过点D作DF⊥AE于点F,连结BF,若DF=AB.下列结论:①DE平分∠AEC;②△ADE 为等腰三角形;③AF=AB;④AE=BE+EF.其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共15分)
11. 一组数据x ,x ,x ,…, xn 的平均数为5,则数据 的平均数是 .
12. 如图,在 中, ,点D在AC边上,以CB、CD 为边作 则 的度数是 .
13. 小颖在解分式方程 时,△处被污染看不清,小明告诉她这里是一个与x无关的常数,且这道题的正确答案是:此方程无解.请你帮小颖猜测一下△处的数应是 .
14. 如图,正方形ABCD的各边分别平行于x轴或y轴,蚂蚁甲和蚂蚁乙都由点E(3,0)出发,同时沿正方形ABCD 的边逆时针匀速运动,蚂蚁甲的速度为3个单位长度/秒,蚂蚁乙的速度为1个单位长度/秒,则两只蚂蚁出发后,蚂蚁甲第3次追上蚂蚁乙的坐标是 .
15. 如图,在矩形ABCD中,AE平分∠BAD交BC于点E,∠CAE=15°.下列结论:( 是等边三角形;②∠AOE=135°;③S△AOE =S△COE.其中正确结论的个数为 .
三、解答题(共75 分)
16. (6分)已知 请用“<”把它们按从小到大的顺序连接起来,说明理由.
17. (8分)如图,在 中,对角线AC与BD相交于点O,点E、F分别为OB、OD的中点,延长AE 至点 G,使. 连结CG.
(1)求证:
(2)当AB 与AC 满足什么数量关系时,四边形 EGCF 是矩形 请说明理由.
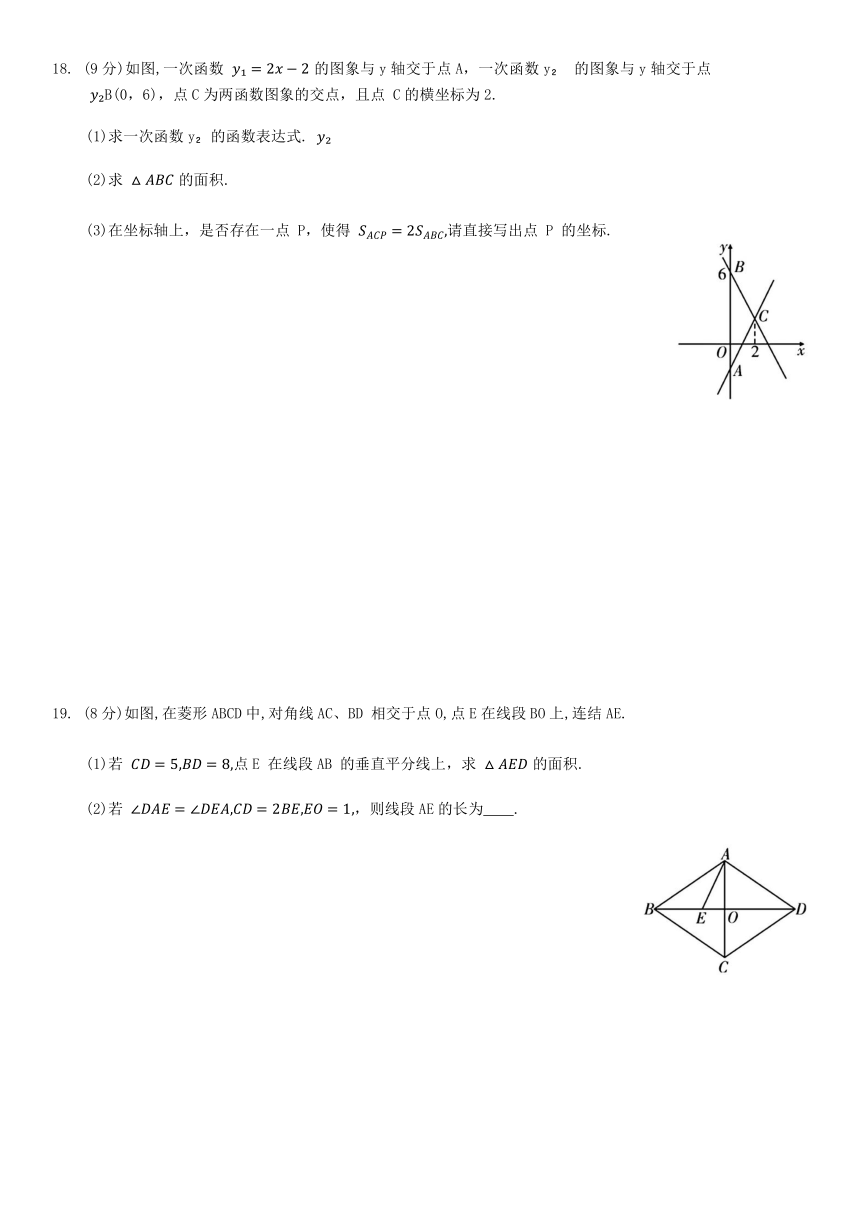
18. (9分)如图,一次函数 的图象与y轴交于点A,一次函数y 的图象与y轴交于点 B(0,6),点C为两函数图象的交点,且点 C的横坐标为2.
(1)求一次函数y 的函数表达式.
(2)求 的面积.
(3)在坐标轴上,是否存在一点 P,使得 请直接写出点 P 的坐标.
19. (8分)如图,在菱形ABCD中,对角线AC、BD 相交于点O,点E在线段BO上,连结AE.
(1)若 点E 在线段AB 的垂直平分线上,求 的面积.
(2)若 ,则线段AE的长为 .
20. (10分)某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图所示的尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
甲、乙两人射箭成绩统计表
次序 第1次 第2次 第3次 第4次 第5次
甲 9 4 7 4 6
乙 7 5 7 a 7
甲、乙两人射箭成绩折线统计图
小宇的作业
解:
根据以上信息,解答下列问题:
(2)请完成图中表示乙变化情况的折线.
(3)①观察统计图,可看出 (填“甲”或“乙”)的成绩比较稳定,参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.
②请你从平均数和方差的角度分析,谁将被选出参加集训.
21. (10分)阅读材料,完成下列任务:
部分分式分解
我们知道,将一个多项式转化成若干整式的积的形式,叫做分解因式.分解因式的结果中,每一个因式的次数都低于原来多项式的次数.而有一些特殊的分式可以分解成若干分式的和的形式,我们称之为部分分式分解.
例如:将 部分分式分解的方法如下:
因为
所以设
去分母,得6=A(x-3)+B(x+3).
整理,得6=(A+B)x+3(B-A).
所以解得
所以 即
显然,部分分式分解的结果中,各分母的次数都低于原分式分母的次数.
任务:
(1)将 部分分式分解.
(2)已知 部分分式分解的结果是 求M、N的值.
22. (12分)已知,如图,在等边三角形ABC中,点D 为直线BC上一点(不与点B、C重合),连结AD,将AD绕点A 逆时针旋转 到AE,连结DE.过点 E作 交直线AB 于点 F.
(1)如图1,点 D 在线段 BC 上.
①猜想线段AC、DC、CE 之间的数量关系,并说明理由.
②求证:
(2)如图2,当点D在BC的延长线上时,(1)中的两个结论是否仍然成立,说明理由.
23. (12分)图象是函数性质的直观载体,通过图象我们容易把握函数的整体性质,下面我们就一类特殊的函数展开探索,经历分析表达式、列表、描点、连线过程得到函数 的图象如图所示.
观察发现:三个函数的图象都是双曲线,且分别关于直线 对称,三个函数表达式中分式部分完全相同,则图象的大小和形状完全相同,只有位置和对称轴发生了变化.因此,我们可以通过描点或平移的方法画函数图象.
(1)平移函数 的图象可以得到函数 的图象,分别写出平移的方向和距离.
(2)探索思考:在所给的平面直角坐标系中,请用你喜欢的方法画出函数 的图象,并写出这个函数的一条性质.
(3)拓展应用:若直线 过点(2,5),(6,3),结合你所画的函数图象,直接写出不等式 的解集.
期末综合测试卷(一)
1. C 2. B 3. A 4. B 5. B 6. B 7. B 8. A 9. A 10. C11. 10 12. 70° 13. 1 14. ( - 1,0) 15. 3
16. 解:
17. (1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,OB=OD,OA=OC,∴∠ABE=∠CDF.∵点E、F分别为OB、OD的中点,∴ 在△ABE 和△CDF中,
∴ △ABE≌△CDF(S. A. S.).
(2)解:当AC=2AB时,四边形 EGCF是矩形.理由如下:
∵AC=2OA,AC=2AB,∴AB=OA,∵E是OB的中点,AG⊥OB,
∴∠OEG=90°,同理,CF⊥OD,∴AG∥CF,即EG∥CF,
∵△ABE≌△CDF,∴AE=CF,∵EG=AE,∴EG=CF,
∴ 四边形EGCF是平行四边形,∵∠OEG=90°,
∴ 四边形 EGCF是矩形.
18. 解:(1)当x=2时,y =2x-2=2,∴C(2,2),设 把B(0,6)、C(2,2)代入可得 解得 ∴一次函数y 的函数表达式为
(2)对于一次函数 令x=0,则
①当点 P在y轴上时, 即 又∵A(0,-2),∴P(0,14)或(0,-18);②当点P在x轴上时,设直线 的图象与x轴交于点D,令y=0,则x=1,∴D(1,0),∴S△ACP =S△ADP +S△PCD = PD
又∵D(1,0),∴P(-7,0)或(9,0).综上,在坐标轴上,存在一点P,使得 此时P点的坐标为(0,14)或(0,-18)或(-7,0)或(9,0).
19. 解:(1)∵四边形ABCD 是菱形,∴( AD=CD.∵CD=5,BD=8,∴AD=5,OB=OD=4.在Rt△AOD中, 点 E在线段AB 的垂直平分线上,∴AE=BE.设AE=BE=x,则OE=4-x.
在Rt△AOE中,∠ ,由勾股定理得 即 解得 则
(2)设. 则 四边形ABCD为菱形,. 王雪2 解得 则 在 中, 在 中,
20. 解:(1)由题意,得( 则 故答案为:4;6.
(2)如图所示.
甲、乙两人射箭成绩折线统计图
(3)①乙
乙射箭成绩的方差为 由于乙射箭成绩的方差小于甲,所以上述判断正确.
②因为 即两人成绩的平均水平(平均数)相同,又∵乙的成绩比甲稳定,所以乙将被选中.
21. 解: .设 去分母,得: ,整理,得 所以 解得所以 即
解得
22. (1)①解: 理由如下: 是等边三角形, .由旋转可知, ∠DAE=60°,∴∠BAD +∠DAC=∠DAC+∠CAE,∴ ∠BAD =
∠CAE,在△BAD 和△CAE中,
∴ △BAD≌△CAE(S. A. S.).
∴BD=CE,∵ BC=BD+CD,BC=AC,∴AC=CE+CD.
②证明:由①知△BAD≌△CAE,则∠ACE=∠B=60°.
又∵∠BAC=60°,∴∠BAC=∠ACE,∴AB∥CE.又∵EF∥BC,
∴ 四边形 BCEF 是平行四边形.∴EF=BC.
(2)结论①AC=CE+CD不成立;结论②EF=BC成立.
理由如下:∵ △ABC 是等边三角形,∴AC =AB = CB,∠B =
∠BAC=60°,∵AD绕点 A 逆时针旋转60°到AE,∴AD =AE,
∠DAE=60°. ∴ ∠BAC =∠DAE.∵ ∠BAD = ∠BAC +∠CAD,
∠CAE = ∠DAE +∠CAD,∴ ∠BAD = ∠CAE,在 △BAD 和
△CAE中
∴CE=BD,∠ACE=∠B=60°,∵BD=BC+CD,BC=AC,
∴CE=AC+CD.∠BAC=60°,∴∠BAC=∠ACE,∴AB∥CE,又∵EF∥BC,∴四边形BCEF是平行四边形.∴EF=BC.
23. 解: 与 相比较,当x相同时,y的值增加1,即函数 图象向上平移1 个单位长度; 与 相比较,当x相同时,y的值减小1,即函数 图象向下平移1个单位长度;所以函数 是由函数 的图象向上平移一个单位长度得到;函数 的图象是由函数 的图象向下平移1 个单位长度得到.
(2)函数 由题知函数 的图象是由函数 的图象向上平移2个单位长度得到的.如图所示:
这个函数的图象关于直线 对称(性质不唯一).
(3)由函数图象可知, 与 都过点(2,5),(6,3),且当x<0或2 时, 的图象在 的下方,当x=2或 时, 故不等式 的解集为: 或
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
1. 在下列给出的条件中,能判定四边形 ABCD 为平行四边形的是 ( )
A. AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C. AB∥CD,AB=CD D. AB=AD,CB=CD
2. 分式 化简后的结果为 ( )
3. 某校九年级(1)班部分学生上学路上所花的时间如图所示.设他们上学路上所花时间的平均数为a,中位数为b,众数为c,则有 ( )
A. b>a>c
B. c>a>b
C. a>b>c
D. b>c>a
4. 在同一直角坐标系中,一次函数y= kx+b和y= bx+k的图象可能是 ( )
5. 如图,点E在正方形ABCD 的边 CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点 G.若BG=3,CG=2,则CE的长为 ( )
C.4
6. 为有效解决交通拥堵问题,营造路网微循环,某市决定对一条长860m的道路进行改造拓宽,为了尽量减轻施工对城市交通造成的影响,实际施工时,每天改造道路的长度比原计划增加10%,结果提前6天完成任务,求实际每天改造道路的长度与实际施工天数.嘉琪同学根据题意列出方程: 则方程中未知数x所表示的量是 ( )
A.实际每天改造道路的长度 B.原计划每天改造道路的长度
C.原计划施工的天数 D.实际施工的天数
7. 如图,菱形ABCD的边长为13,对角线AC的长为24,延长AB 至点E,BF平分∠CBE,点G是BF上任意一点,则△ACG的面积为 ( )
A.30 B.60 C.90 D.120
8. 如图,在平面直角坐标系中,PB⊥PA,AB⊥x轴于点E,正比例函数y= mx的图象和反比例函数 的图象相交于A、P( -1,2)两点,则点B 的坐标是 ( )
A.(1,3) B.(1,4) C.(1,5) D.(1,6)
9. 甲、乙两名运动员10次射击成绩(单位:环)如图所示. 甲、乙两名运动员射击成绩的平均数记为 则下列结论中完全正确的是 ( )
10. 如图,点E为矩形ABCD的边BC上的点,连结AE、DE,过点D作DF⊥AE于点F,连结BF,若DF=AB.下列结论:①DE平分∠AEC;②△ADE 为等腰三角形;③AF=AB;④AE=BE+EF.其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共15分)
11. 一组数据x ,x ,x ,…, xn 的平均数为5,则数据 的平均数是 .
12. 如图,在 中, ,点D在AC边上,以CB、CD 为边作 则 的度数是 .
13. 小颖在解分式方程 时,△处被污染看不清,小明告诉她这里是一个与x无关的常数,且这道题的正确答案是:此方程无解.请你帮小颖猜测一下△处的数应是 .
14. 如图,正方形ABCD的各边分别平行于x轴或y轴,蚂蚁甲和蚂蚁乙都由点E(3,0)出发,同时沿正方形ABCD 的边逆时针匀速运动,蚂蚁甲的速度为3个单位长度/秒,蚂蚁乙的速度为1个单位长度/秒,则两只蚂蚁出发后,蚂蚁甲第3次追上蚂蚁乙的坐标是 .
15. 如图,在矩形ABCD中,AE平分∠BAD交BC于点E,∠CAE=15°.下列结论:( 是等边三角形;②∠AOE=135°;③S△AOE =S△COE.其中正确结论的个数为 .
三、解答题(共75 分)
16. (6分)已知 请用“<”把它们按从小到大的顺序连接起来,说明理由.
17. (8分)如图,在 中,对角线AC与BD相交于点O,点E、F分别为OB、OD的中点,延长AE 至点 G,使. 连结CG.
(1)求证:
(2)当AB 与AC 满足什么数量关系时,四边形 EGCF 是矩形 请说明理由.
18. (9分)如图,一次函数 的图象与y轴交于点A,一次函数y 的图象与y轴交于点 B(0,6),点C为两函数图象的交点,且点 C的横坐标为2.
(1)求一次函数y 的函数表达式.
(2)求 的面积.
(3)在坐标轴上,是否存在一点 P,使得 请直接写出点 P 的坐标.
19. (8分)如图,在菱形ABCD中,对角线AC、BD 相交于点O,点E在线段BO上,连结AE.
(1)若 点E 在线段AB 的垂直平分线上,求 的面积.
(2)若 ,则线段AE的长为 .
20. (10分)某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如图所示的尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
甲、乙两人射箭成绩统计表
次序 第1次 第2次 第3次 第4次 第5次
甲 9 4 7 4 6
乙 7 5 7 a 7
甲、乙两人射箭成绩折线统计图
小宇的作业
解:
根据以上信息,解答下列问题:
(2)请完成图中表示乙变化情况的折线.
(3)①观察统计图,可看出 (填“甲”或“乙”)的成绩比较稳定,参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.
②请你从平均数和方差的角度分析,谁将被选出参加集训.
21. (10分)阅读材料,完成下列任务:
部分分式分解
我们知道,将一个多项式转化成若干整式的积的形式,叫做分解因式.分解因式的结果中,每一个因式的次数都低于原来多项式的次数.而有一些特殊的分式可以分解成若干分式的和的形式,我们称之为部分分式分解.
例如:将 部分分式分解的方法如下:
因为
所以设
去分母,得6=A(x-3)+B(x+3).
整理,得6=(A+B)x+3(B-A).
所以解得
所以 即
显然,部分分式分解的结果中,各分母的次数都低于原分式分母的次数.
任务:
(1)将 部分分式分解.
(2)已知 部分分式分解的结果是 求M、N的值.
22. (12分)已知,如图,在等边三角形ABC中,点D 为直线BC上一点(不与点B、C重合),连结AD,将AD绕点A 逆时针旋转 到AE,连结DE.过点 E作 交直线AB 于点 F.
(1)如图1,点 D 在线段 BC 上.
①猜想线段AC、DC、CE 之间的数量关系,并说明理由.
②求证:
(2)如图2,当点D在BC的延长线上时,(1)中的两个结论是否仍然成立,说明理由.
23. (12分)图象是函数性质的直观载体,通过图象我们容易把握函数的整体性质,下面我们就一类特殊的函数展开探索,经历分析表达式、列表、描点、连线过程得到函数 的图象如图所示.
观察发现:三个函数的图象都是双曲线,且分别关于直线 对称,三个函数表达式中分式部分完全相同,则图象的大小和形状完全相同,只有位置和对称轴发生了变化.因此,我们可以通过描点或平移的方法画函数图象.
(1)平移函数 的图象可以得到函数 的图象,分别写出平移的方向和距离.
(2)探索思考:在所给的平面直角坐标系中,请用你喜欢的方法画出函数 的图象,并写出这个函数的一条性质.
(3)拓展应用:若直线 过点(2,5),(6,3),结合你所画的函数图象,直接写出不等式 的解集.
期末综合测试卷(一)
1. C 2. B 3. A 4. B 5. B 6. B 7. B 8. A 9. A 10. C11. 10 12. 70° 13. 1 14. ( - 1,0) 15. 3
16. 解:
17. (1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,OB=OD,OA=OC,∴∠ABE=∠CDF.∵点E、F分别为OB、OD的中点,∴ 在△ABE 和△CDF中,
∴ △ABE≌△CDF(S. A. S.).
(2)解:当AC=2AB时,四边形 EGCF是矩形.理由如下:
∵AC=2OA,AC=2AB,∴AB=OA,∵E是OB的中点,AG⊥OB,
∴∠OEG=90°,同理,CF⊥OD,∴AG∥CF,即EG∥CF,
∵△ABE≌△CDF,∴AE=CF,∵EG=AE,∴EG=CF,
∴ 四边形EGCF是平行四边形,∵∠OEG=90°,
∴ 四边形 EGCF是矩形.
18. 解:(1)当x=2时,y =2x-2=2,∴C(2,2),设 把B(0,6)、C(2,2)代入可得 解得 ∴一次函数y 的函数表达式为
(2)对于一次函数 令x=0,则
①当点 P在y轴上时, 即 又∵A(0,-2),∴P(0,14)或(0,-18);②当点P在x轴上时,设直线 的图象与x轴交于点D,令y=0,则x=1,∴D(1,0),∴S△ACP =S△ADP +S△PCD = PD
又∵D(1,0),∴P(-7,0)或(9,0).综上,在坐标轴上,存在一点P,使得 此时P点的坐标为(0,14)或(0,-18)或(-7,0)或(9,0).
19. 解:(1)∵四边形ABCD 是菱形,∴( AD=CD.∵CD=5,BD=8,∴AD=5,OB=OD=4.在Rt△AOD中, 点 E在线段AB 的垂直平分线上,∴AE=BE.设AE=BE=x,则OE=4-x.
在Rt△AOE中,∠ ,由勾股定理得 即 解得 则
(2)设. 则 四边形ABCD为菱形,. 王雪2 解得 则 在 中, 在 中,
20. 解:(1)由题意,得( 则 故答案为:4;6.
(2)如图所示.
甲、乙两人射箭成绩折线统计图
(3)①乙
乙射箭成绩的方差为 由于乙射箭成绩的方差小于甲,所以上述判断正确.
②因为 即两人成绩的平均水平(平均数)相同,又∵乙的成绩比甲稳定,所以乙将被选中.
21. 解: .设 去分母,得: ,整理,得 所以 解得所以 即
解得
22. (1)①解: 理由如下: 是等边三角形, .由旋转可知, ∠DAE=60°,∴∠BAD +∠DAC=∠DAC+∠CAE,∴ ∠BAD =
∠CAE,在△BAD 和△CAE中,
∴ △BAD≌△CAE(S. A. S.).
∴BD=CE,∵ BC=BD+CD,BC=AC,∴AC=CE+CD.
②证明:由①知△BAD≌△CAE,则∠ACE=∠B=60°.
又∵∠BAC=60°,∴∠BAC=∠ACE,∴AB∥CE.又∵EF∥BC,
∴ 四边形 BCEF 是平行四边形.∴EF=BC.
(2)结论①AC=CE+CD不成立;结论②EF=BC成立.
理由如下:∵ △ABC 是等边三角形,∴AC =AB = CB,∠B =
∠BAC=60°,∵AD绕点 A 逆时针旋转60°到AE,∴AD =AE,
∠DAE=60°. ∴ ∠BAC =∠DAE.∵ ∠BAD = ∠BAC +∠CAD,
∠CAE = ∠DAE +∠CAD,∴ ∠BAD = ∠CAE,在 △BAD 和
△CAE中
∴CE=BD,∠ACE=∠B=60°,∵BD=BC+CD,BC=AC,
∴CE=AC+CD.∠BAC=60°,∴∠BAC=∠ACE,∴AB∥CE,又∵EF∥BC,∴四边形BCEF是平行四边形.∴EF=BC.
23. 解: 与 相比较,当x相同时,y的值增加1,即函数 图象向上平移1 个单位长度; 与 相比较,当x相同时,y的值减小1,即函数 图象向下平移1个单位长度;所以函数 是由函数 的图象向上平移一个单位长度得到;函数 的图象是由函数 的图象向下平移1 个单位长度得到.
(2)函数 由题知函数 的图象是由函数 的图象向上平移2个单位长度得到的.如图所示:
这个函数的图象关于直线 对称(性质不唯一).
(3)由函数图象可知, 与 都过点(2,5),(6,3),且当x<0或2 时, 的图象在 的下方,当x=2或 时, 故不等式 的解集为: 或
同课章节目录
