初中数学人教版八年级上册 11.1 与三角形有关的线段(第2课时 )三角形的高、中线与角平分线及稳定性 同步提优训练(无答案)
文档属性
| 名称 | 初中数学人教版八年级上册 11.1 与三角形有关的线段(第2课时 )三角形的高、中线与角平分线及稳定性 同步提优训练(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 454.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 00:00:00 | ||
图片预览

文档简介
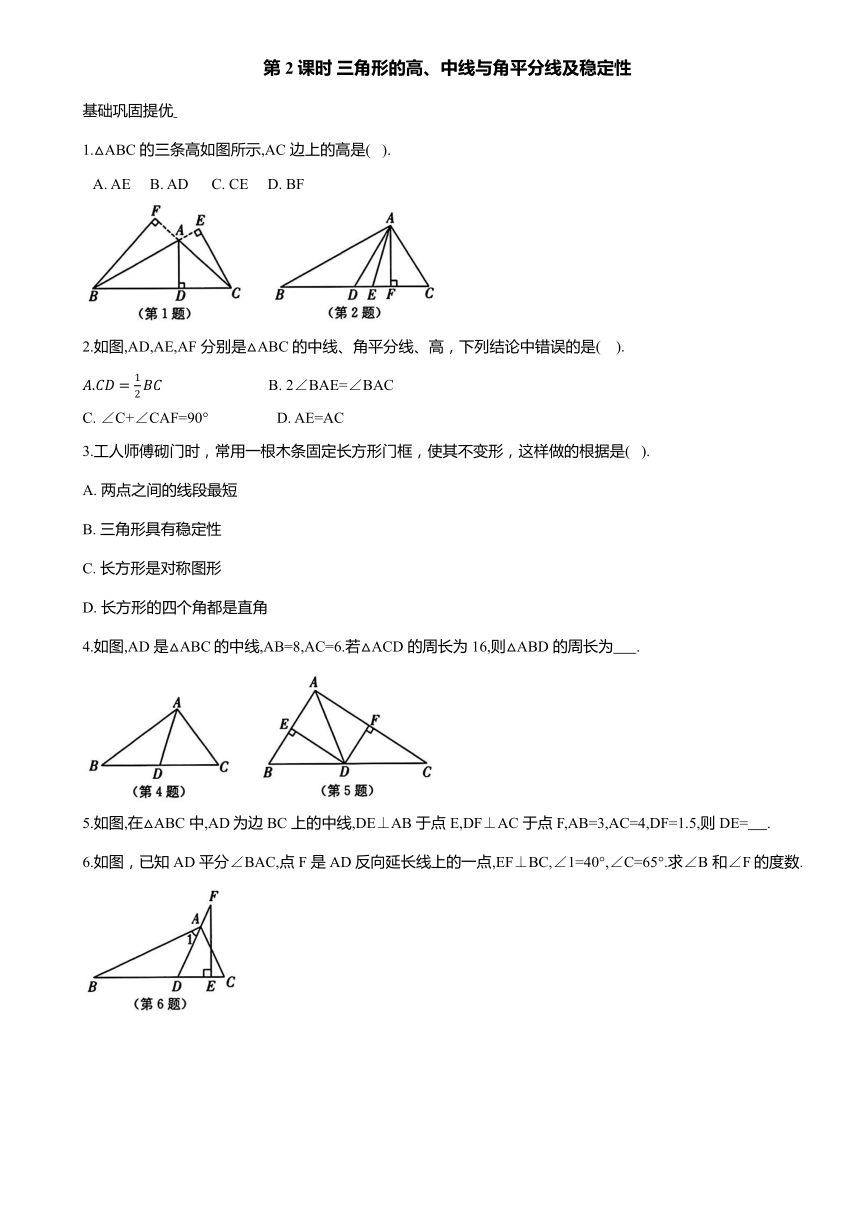
第2课时 三角形的高、中线与角平分线及稳定性
基础巩固提优
1.△ABC 的三条高如图所示,AC 边上的高是( ).
A. AE B. AD C. CE D. BF
2.如图,AD,AE,AF 分别是△ABC 的中线、角平分线、高,下列结论中错误的是( ).
B. 2∠BAE=∠BAC
C. ∠C+∠CAF=90° D. AE=AC
3.工人师傅砌门时,常用一根木条固定长方形门框,使其不变形,这样做的根据是( ).
A. 两点之间的线段最短
B. 三角形具有稳定性
C. 长方形是对称图形
D. 长方形的四个角都是直角
4.如图,AD 是△ABC的中线,AB=8,AC=6.若△ACD 的周长为16,则△ABD 的周长为 .
5.如图,在△ABC 中,AD为边BC 上的中线,DE⊥AB 于点 E,DF⊥AC 于点 F,AB=3,AC=4,DF=1.5,则DE= .
6.如图,已知AD 平分∠BAC,点 F 是AD 反向延长线上的一点,EF⊥BC,∠1=40°,∠C=65°.求∠B 和∠F的度数.
思维拓展提优
7.下面的说法正确的是( ).
A. 三角形的角平分线、中线和高都在三角形内
B. 直角三角形的高只有一条
C. 三角形的高至少有一条在三角形内
D. 钝角三角形的三条高都在三角形外面
8.如图,AD 为△ABC 的角平分线,DE∥AB 交AC 于点E,若∠BAC=100°,则∠ADE= °.
9.如图,在△ABC 中,∠BAD=∠CAD,G为AD 的中点,BG 的延长线交 AC 于点E,F 为AB 上的一点,CF与AD 垂直,交 AD 于点 H,则下面结论:①AD 是△ABE 的角平分线;② BE 是△ABD 的边AD 上的中线;③CH 是△ACD的边AD 上的高;④AH 是△ACF 的角平分线和高.其中正确的有 .(填序号)
10.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,AB=10,则AB边上的高为 .
11. 如图,在△ABC中,AB=AC,P 是边BC 上一点,PE⊥AB,PF⊥AC,BD 是边AC 上的高,若PE=5cm,PF=3cm,则 BD 的长为 .
12. 如图,在△ABC 中,已知点 E,F 分别是边 AD,CE 的中点,且S△ABC =8 cm ,则 S△BEF 的值为
13.如图,AD 是△ABC 的高,CE 是△ACB 的角平分线,F 是 AC 的中点,∠ACB=50°,∠BAD=70°.
(1)求∠AEC 的度数;
(2)若△BCF 与△BAF 的周长差为 3,AB=7,能否求出 BC 的值 若能,请写出理由和结果;若不能,请你补充条件并解答.
延伸探究提优
14.如图,在△ABC中,AD⊥BC,AE 平分∠BAC,∠B=70°,∠C=30°.
(1)求∠BAE 的度数;
(2)求∠DAE 的度数;
(3)探究:小明认为如果条件∠B =70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE 的度数.若能,请你写出求解过程;若不能,请说明理由.
15. 在△ABC 中,AB:AC=3:2,BC=AC+1,若△ABC 的中线BD 把△ABC 的周长分成两部分的比是8:7,求边 AB,AC 的长.
基础巩固提优
1.△ABC 的三条高如图所示,AC 边上的高是( ).
A. AE B. AD C. CE D. BF
2.如图,AD,AE,AF 分别是△ABC 的中线、角平分线、高,下列结论中错误的是( ).
B. 2∠BAE=∠BAC
C. ∠C+∠CAF=90° D. AE=AC
3.工人师傅砌门时,常用一根木条固定长方形门框,使其不变形,这样做的根据是( ).
A. 两点之间的线段最短
B. 三角形具有稳定性
C. 长方形是对称图形
D. 长方形的四个角都是直角
4.如图,AD 是△ABC的中线,AB=8,AC=6.若△ACD 的周长为16,则△ABD 的周长为 .
5.如图,在△ABC 中,AD为边BC 上的中线,DE⊥AB 于点 E,DF⊥AC 于点 F,AB=3,AC=4,DF=1.5,则DE= .
6.如图,已知AD 平分∠BAC,点 F 是AD 反向延长线上的一点,EF⊥BC,∠1=40°,∠C=65°.求∠B 和∠F的度数.
思维拓展提优
7.下面的说法正确的是( ).
A. 三角形的角平分线、中线和高都在三角形内
B. 直角三角形的高只有一条
C. 三角形的高至少有一条在三角形内
D. 钝角三角形的三条高都在三角形外面
8.如图,AD 为△ABC 的角平分线,DE∥AB 交AC 于点E,若∠BAC=100°,则∠ADE= °.
9.如图,在△ABC 中,∠BAD=∠CAD,G为AD 的中点,BG 的延长线交 AC 于点E,F 为AB 上的一点,CF与AD 垂直,交 AD 于点 H,则下面结论:①AD 是△ABE 的角平分线;② BE 是△ABD 的边AD 上的中线;③CH 是△ACD的边AD 上的高;④AH 是△ACF 的角平分线和高.其中正确的有 .(填序号)
10.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,AB=10,则AB边上的高为 .
11. 如图,在△ABC中,AB=AC,P 是边BC 上一点,PE⊥AB,PF⊥AC,BD 是边AC 上的高,若PE=5cm,PF=3cm,则 BD 的长为 .
12. 如图,在△ABC 中,已知点 E,F 分别是边 AD,CE 的中点,且S△ABC =8 cm ,则 S△BEF 的值为
13.如图,AD 是△ABC 的高,CE 是△ACB 的角平分线,F 是 AC 的中点,∠ACB=50°,∠BAD=70°.
(1)求∠AEC 的度数;
(2)若△BCF 与△BAF 的周长差为 3,AB=7,能否求出 BC 的值 若能,请写出理由和结果;若不能,请你补充条件并解答.
延伸探究提优
14.如图,在△ABC中,AD⊥BC,AE 平分∠BAC,∠B=70°,∠C=30°.
(1)求∠BAE 的度数;
(2)求∠DAE 的度数;
(3)探究:小明认为如果条件∠B =70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE 的度数.若能,请你写出求解过程;若不能,请说明理由.
15. 在△ABC 中,AB:AC=3:2,BC=AC+1,若△ABC 的中线BD 把△ABC 的周长分成两部分的比是8:7,求边 AB,AC 的长.
