24.2.1 点和圆的位置关系 同步练 2024--2025学年上学期初中数学人教版九年级上册
文档属性
| 名称 | 24.2.1 点和圆的位置关系 同步练 2024--2025学年上学期初中数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 525.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-18 19:02:22 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.2.1 点和圆的位置关系 同步练
2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.若的半径为,点A到圆心O的距离为,那么点A与的位置关系是( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.不能确定
2.在数轴上,点所表示的实数为3,点所表示的实数为,的半径为2.下列说法中不正确的是( )
A.当时,点在上 B.当时,点在内
C.当时,点在内 D.当时,点在外
3.的半径为,点A在外,则的长可以是( )
A. B. C. D.
4.如图,在△ABC中,AB=AC,BC=4,tanB=2,以AB的中点D为圆心,r为半径作⊙D,如果点B在⊙D内,点C在⊙D外,那么r可以取( )
A.2 B.3 C.4 D.5
5.如图,中,是内部的一个动点,且满足,则线段长的最小值为()
A.1 B.1.6 C. D.2
6.如图,矩形ABCD中,∠BAC=60°,点E在AB上,且BE:AB=1:3,点F在BC边上运动,以线段EF为斜边在点B的异侧作等腰直角三角形GEF,连接CG,当CG最小时,的值为( )
A. B. C. D.
7.如图,已知平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )
A.(6,8) B.(4,5) C.(4,) D.(4,)
8.直角三角形的两边长分别为和,则此三角形的外接圆半径是( )
A.或 B.或 C. D.
二、填空题
9.若一个点到圆心的距离恰好等于半径,则此点必在 ;若一个点到圆心的距离大于半径,则此点必在 ;若一个点到圆心的距离小于半径,则此点必在 .
10.在Rt△ABC中,∠C=90°,AC=2cm,BC=4cm,若以点C为圆心,2cm为半径作圆,则点A在⊙C ,点B在⊙C .
11.如图,,等边三角形的两个顶点、分别在、上移动,,则的最大值是
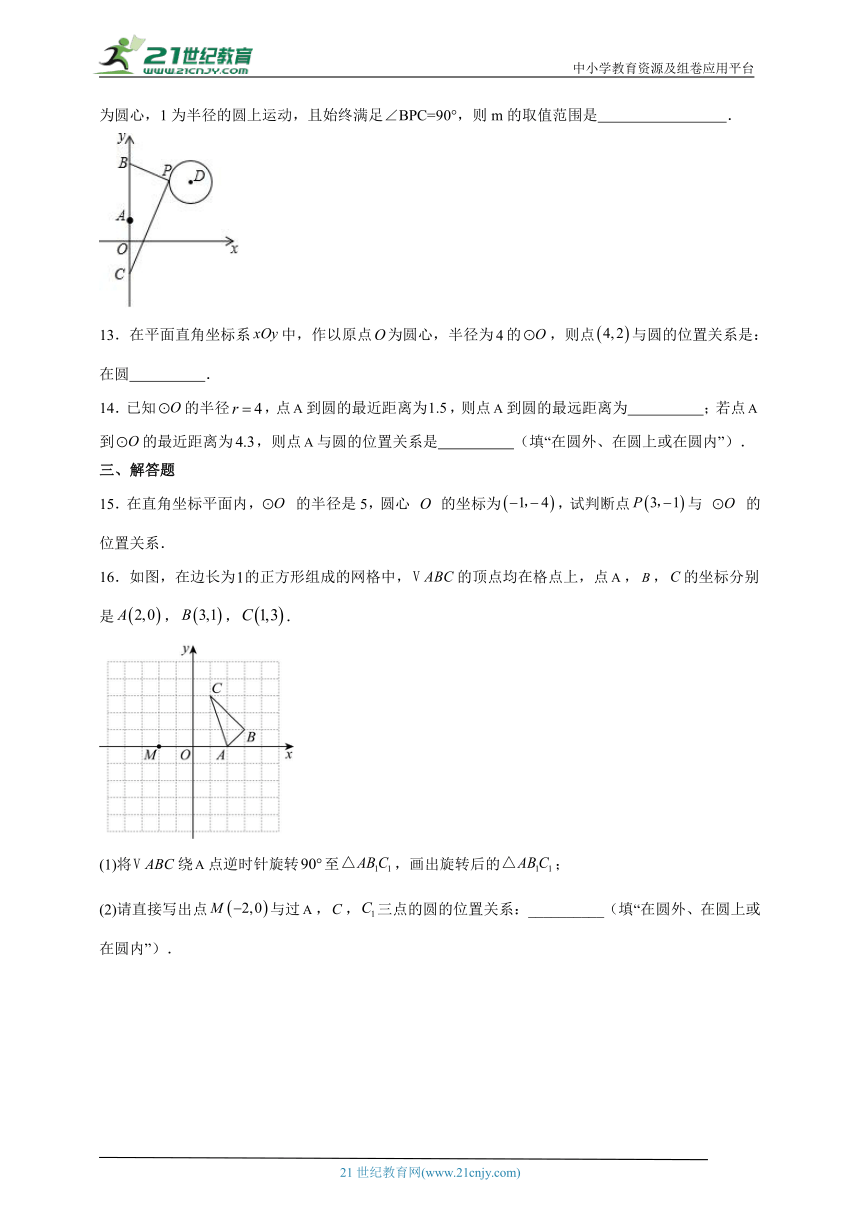
12.如图,在平面直角坐标系中,已知点、、(m>0),点P在以D(4,5)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则m的取值范围是 .
13.在平面直角坐标系中,作以原点为圆心,半径为的,则点与圆的位置关系是:在圆 .
14.已知的半径,点到圆的最近距离为,则点到圆的最远距离为 ;若点到的最近距离为,则点与圆的位置关系是 (填“在圆外、在圆上或在圆内”).
三、解答题
15.在直角坐标平面内, 的半径是5,圆心 的坐标为,试判断点与 的位置关系.
16.如图,在边长为的正方形组成的网格中,的顶点均在格点上,点,,的坐标分别是,,.
(1)将绕点逆时针旋转至,画出旋转后的;
(2)请直接写出点与过,,三点的圆的位置关系:__________(填“在圆外、在圆上或在圆内”).
参考答案:
1.B
解:∵的半径为,点A到圆心O的距离为,,
∴点A与的位置关系是点A在圆内,
2.C
解:A.当时,,即,点在上,故A正确;
B.当时,,即,点在内,故B正确;
C.当时,①时,,即,点在外;②时,,即,点在上;③时,,即,点在内;故C不正确;
D.当时,,即,点在外,故D正确;
3.D
解:当点A在外时,;
A、B、C选项均不符合;
4.B
如图,过点A作AF⊥BC于点F,连接CD交AF于点 G,
∵AB=AC,BC=4,
∴BF=CF=2,
∵tanB=2,
∴,即AF=4,
∴AB=,
∵D为AB的中点,
∴BD=,G是△ABC的重心,
∴GF=AF=,
∴CG= ,
∴CD=CG=,
∵点B在⊙D内,点C在⊙D外,
∴<r<,
5.C
解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴点P在以AB为直径的圆O上,连接OC交圆O于点P,此时PC最小
在Rt△BCO中,∠OBC=90°,BC=3,OB=AB=2,
∴OC=
∴=.
6.A
解:如图1,取EF的中点O,连接OB,OG,作射线BG,
∵四边形ABCD是矩形,
∴∠ABC=90°
∵O是EF的中点,
∴OB=OE=OF
∵∠EGF=90°,O是EF的中点,
∴OG=OE=OF
∴OB=OG=OE=OF
∴B,E,G,在以O为圆心的圆上,
∴∠EBG=∠EFG,
∵∠EGF=90°, EG=FG,
∴∠GEF=∠GFE=45°
∴∠EBG=45°
∴BG平分∠ABC,
∴点G在∠ABC的平分线上,
当CG⊥BG时,CG最小,
此时,如图2,
∵BG平分∠ABC,
∴∠ABG=∠GBC=∠ABC=45°,
∵CG⊥BG
∴△BCG是以BC为斜边的等腰直角三角形,∠BGC=90°
∴BG=CG
∵∠EGF=∠BGC=90°
∴∠EGF-∠BGF=∠BGC-∠BGF,
∴∠EGB=∠FGC,
在△EGB和△FGC中,
∴△EGB≌△FGC(SAS),
∴BE=CF
∵四边形ABCD是矩形,
∴AD=BC
设AB=m
∵BE∶AB=1∶3
∴CF=BE=m,
在Rt△ABC中,∠BAC=60°,
∴∠ACB =30°
∴AC =2AB= 2m
∴BC= ,
∴AD=m,
∴
7.C
解:∵⊙P经过点A、B、C,
∴点P在线段AB的垂直平分线上,
∴点P的横坐标为4,
设点P的坐标为(4,y),
作PE⊥OB于E,PF⊥OC于F,
由题意得:,
解得,y,
8.B
解:由勾股定理可知: ①当直角三角形的斜边长为时,这个三角形的外接圆半径为; ②当两条直角边长分别为和,则直角三角形的斜边长 因此这个三角形的外接圆半径为.
综上所述:这个三角形的外接圆半径等于或.
9. 圆上 圆外 圆内
解:圆上的点到圆心的距离等于半径,所以到圆心距离等于半径的点在圆上.
圆外的点到圆心的距离大于半径,所以到圆心距离大于半径的点在圆外.
圆内的点到圆心的距离小于半径,所以到圆心距离小于半径的点在圆内.
故答案为圆上,圆外,圆内.
10. 上 外
∵⊙C的半径为2cm,
而AC=2cm,BC=4cm,
∴点A在⊙C上;点B在⊙C外;
故答案为上、外.
11.
解:∵AB=2为定线,∠XOY=45°为定角,
∴当两个顶点A、B分别在OX、OY上移动时,即为点O在以AB为弦所含的圆周角为45°的弧上运动,
设A,B,O三点所在圆的圆心为M,
当O,M,C三点共线时,OC的值最大,
如图,连接AM,BM,
∵△ABC是等边三角形,
∴AC=BC,
∵AM=BM,
∴OC垂直平分AB,
∵∠AOB=45°,
∴∠AMB=90°,
∵AB=2,
∴AM=,DM=AD=BD=1,
∴OM=,CD=,
∴OC=DM+OM+CD=,
故答案为:.
12.
连接AP,作射线AD,
由题意得,AB=,AC=
,D(4,5)
当点P在线段AD的延长线上时,AP最长,即AP=5+1=6;
当点P在线段AD上时,AP最短,即AP=5-1=4,
的取值范围是:,
故答案为:.
13.外
解:点到圆心的距离,
∵,
∴点在外,
故答案为:外.
14. 或 在圆外
解:的半径,点到圆的最近距离为,
点在圆内或者圆外,
当点在圆内时,点到圆的最远距离为:;
当点在圆外时,点到圆的最远距离为:;
当点到的最近距离,的半径,,
此时点在圆外;
故答案为:或,点在圆外.
15.点在 上
解:,
因为半径为5,
所以点在 上.
16.(1)作图见解析
(2)在圆上
(1)解:如图,为所作;
(2)由(1)可知:,,
∴为等腰直角三角形,
∴的外接圆的圆心为的中点,
又∵网格中的小正方形的边长为,
∴,
,,
∴,,
在和中,
∴,
∴,
∴,
∵,
∴,
∴,
∴点在过,,三点的圆上,
故答案为:在圆上.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.2.1 点和圆的位置关系 同步练
2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.若的半径为,点A到圆心O的距离为,那么点A与的位置关系是( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.不能确定
2.在数轴上,点所表示的实数为3,点所表示的实数为,的半径为2.下列说法中不正确的是( )
A.当时,点在上 B.当时,点在内
C.当时,点在内 D.当时,点在外
3.的半径为,点A在外,则的长可以是( )
A. B. C. D.
4.如图,在△ABC中,AB=AC,BC=4,tanB=2,以AB的中点D为圆心,r为半径作⊙D,如果点B在⊙D内,点C在⊙D外,那么r可以取( )
A.2 B.3 C.4 D.5
5.如图,中,是内部的一个动点,且满足,则线段长的最小值为()
A.1 B.1.6 C. D.2
6.如图,矩形ABCD中,∠BAC=60°,点E在AB上,且BE:AB=1:3,点F在BC边上运动,以线段EF为斜边在点B的异侧作等腰直角三角形GEF,连接CG,当CG最小时,的值为( )
A. B. C. D.
7.如图,已知平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )
A.(6,8) B.(4,5) C.(4,) D.(4,)
8.直角三角形的两边长分别为和,则此三角形的外接圆半径是( )
A.或 B.或 C. D.
二、填空题
9.若一个点到圆心的距离恰好等于半径,则此点必在 ;若一个点到圆心的距离大于半径,则此点必在 ;若一个点到圆心的距离小于半径,则此点必在 .
10.在Rt△ABC中,∠C=90°,AC=2cm,BC=4cm,若以点C为圆心,2cm为半径作圆,则点A在⊙C ,点B在⊙C .
11.如图,,等边三角形的两个顶点、分别在、上移动,,则的最大值是
12.如图,在平面直角坐标系中,已知点、、(m>0),点P在以D(4,5)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则m的取值范围是 .
13.在平面直角坐标系中,作以原点为圆心,半径为的,则点与圆的位置关系是:在圆 .
14.已知的半径,点到圆的最近距离为,则点到圆的最远距离为 ;若点到的最近距离为,则点与圆的位置关系是 (填“在圆外、在圆上或在圆内”).
三、解答题
15.在直角坐标平面内, 的半径是5,圆心 的坐标为,试判断点与 的位置关系.
16.如图,在边长为的正方形组成的网格中,的顶点均在格点上,点,,的坐标分别是,,.
(1)将绕点逆时针旋转至,画出旋转后的;
(2)请直接写出点与过,,三点的圆的位置关系:__________(填“在圆外、在圆上或在圆内”).
参考答案:
1.B
解:∵的半径为,点A到圆心O的距离为,,
∴点A与的位置关系是点A在圆内,
2.C
解:A.当时,,即,点在上,故A正确;
B.当时,,即,点在内,故B正确;
C.当时,①时,,即,点在外;②时,,即,点在上;③时,,即,点在内;故C不正确;
D.当时,,即,点在外,故D正确;
3.D
解:当点A在外时,;
A、B、C选项均不符合;
4.B
如图,过点A作AF⊥BC于点F,连接CD交AF于点 G,
∵AB=AC,BC=4,
∴BF=CF=2,
∵tanB=2,
∴,即AF=4,
∴AB=,
∵D为AB的中点,
∴BD=,G是△ABC的重心,
∴GF=AF=,
∴CG= ,
∴CD=CG=,
∵点B在⊙D内,点C在⊙D外,
∴<r<,
5.C
解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴点P在以AB为直径的圆O上,连接OC交圆O于点P,此时PC最小
在Rt△BCO中,∠OBC=90°,BC=3,OB=AB=2,
∴OC=
∴=.
6.A
解:如图1,取EF的中点O,连接OB,OG,作射线BG,
∵四边形ABCD是矩形,
∴∠ABC=90°
∵O是EF的中点,
∴OB=OE=OF
∵∠EGF=90°,O是EF的中点,
∴OG=OE=OF
∴OB=OG=OE=OF
∴B,E,G,在以O为圆心的圆上,
∴∠EBG=∠EFG,
∵∠EGF=90°, EG=FG,
∴∠GEF=∠GFE=45°
∴∠EBG=45°
∴BG平分∠ABC,
∴点G在∠ABC的平分线上,
当CG⊥BG时,CG最小,
此时,如图2,
∵BG平分∠ABC,
∴∠ABG=∠GBC=∠ABC=45°,
∵CG⊥BG
∴△BCG是以BC为斜边的等腰直角三角形,∠BGC=90°
∴BG=CG
∵∠EGF=∠BGC=90°
∴∠EGF-∠BGF=∠BGC-∠BGF,
∴∠EGB=∠FGC,
在△EGB和△FGC中,
∴△EGB≌△FGC(SAS),
∴BE=CF
∵四边形ABCD是矩形,
∴AD=BC
设AB=m
∵BE∶AB=1∶3
∴CF=BE=m,
在Rt△ABC中,∠BAC=60°,
∴∠ACB =30°
∴AC =2AB= 2m
∴BC= ,
∴AD=m,
∴
7.C
解:∵⊙P经过点A、B、C,
∴点P在线段AB的垂直平分线上,
∴点P的横坐标为4,
设点P的坐标为(4,y),
作PE⊥OB于E,PF⊥OC于F,
由题意得:,
解得,y,
8.B
解:由勾股定理可知: ①当直角三角形的斜边长为时,这个三角形的外接圆半径为; ②当两条直角边长分别为和,则直角三角形的斜边长 因此这个三角形的外接圆半径为.
综上所述:这个三角形的外接圆半径等于或.
9. 圆上 圆外 圆内
解:圆上的点到圆心的距离等于半径,所以到圆心距离等于半径的点在圆上.
圆外的点到圆心的距离大于半径,所以到圆心距离大于半径的点在圆外.
圆内的点到圆心的距离小于半径,所以到圆心距离小于半径的点在圆内.
故答案为圆上,圆外,圆内.
10. 上 外
∵⊙C的半径为2cm,
而AC=2cm,BC=4cm,
∴点A在⊙C上;点B在⊙C外;
故答案为上、外.
11.
解:∵AB=2为定线,∠XOY=45°为定角,
∴当两个顶点A、B分别在OX、OY上移动时,即为点O在以AB为弦所含的圆周角为45°的弧上运动,
设A,B,O三点所在圆的圆心为M,
当O,M,C三点共线时,OC的值最大,
如图,连接AM,BM,
∵△ABC是等边三角形,
∴AC=BC,
∵AM=BM,
∴OC垂直平分AB,
∵∠AOB=45°,
∴∠AMB=90°,
∵AB=2,
∴AM=,DM=AD=BD=1,
∴OM=,CD=,
∴OC=DM+OM+CD=,
故答案为:.
12.
连接AP,作射线AD,
由题意得,AB=,AC=
,D(4,5)
当点P在线段AD的延长线上时,AP最长,即AP=5+1=6;
当点P在线段AD上时,AP最短,即AP=5-1=4,
的取值范围是:,
故答案为:.
13.外
解:点到圆心的距离,
∵,
∴点在外,
故答案为:外.
14. 或 在圆外
解:的半径,点到圆的最近距离为,
点在圆内或者圆外,
当点在圆内时,点到圆的最远距离为:;
当点在圆外时,点到圆的最远距离为:;
当点到的最近距离,的半径,,
此时点在圆外;
故答案为:或,点在圆外.
15.点在 上
解:,
因为半径为5,
所以点在 上.
16.(1)作图见解析
(2)在圆上
(1)解:如图,为所作;
(2)由(1)可知:,,
∴为等腰直角三角形,
∴的外接圆的圆心为的中点,
又∵网格中的小正方形的边长为,
∴,
,,
∴,,
在和中,
∴,
∴,
∴,
∵,
∴,
∴,
∴点在过,,三点的圆上,
故答案为:在圆上.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
