24.2.2 直线和圆的位置关系 同步练 2024--2025学年上学期初中数学人教版九年级上册
文档属性
| 名称 | 24.2.2 直线和圆的位置关系 同步练 2024--2025学年上学期初中数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 955.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-18 19:02:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.2.2 直线和圆的位置关系 同步练
2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.的半径为,点是直线上的三点,的长度分别是、、,则直线与的位置关系是: ( )
A.相离 B.相切 C.相交 D.不能确定
2.如图,是的切线,连接并延长交于点C.若,则的度数是( )
A. B. C. D.
3.如图,切于,的延长线交于,若,则的度数是
A.72° B.63° C.54° D.36°
4.如图,是的两条切线, 是切点,若,则的半径等于( )
A. B.1 C.2 D.
5.如图,AB是⊙O的直径,弦CD与AB相交,连接CO,过点D作⊙O的切线,与AB的延长线交于点E,若DE∥AC,∠BAC=40°,则∠OCD的度数为( )
A.65° B.30° C.25° D.20°
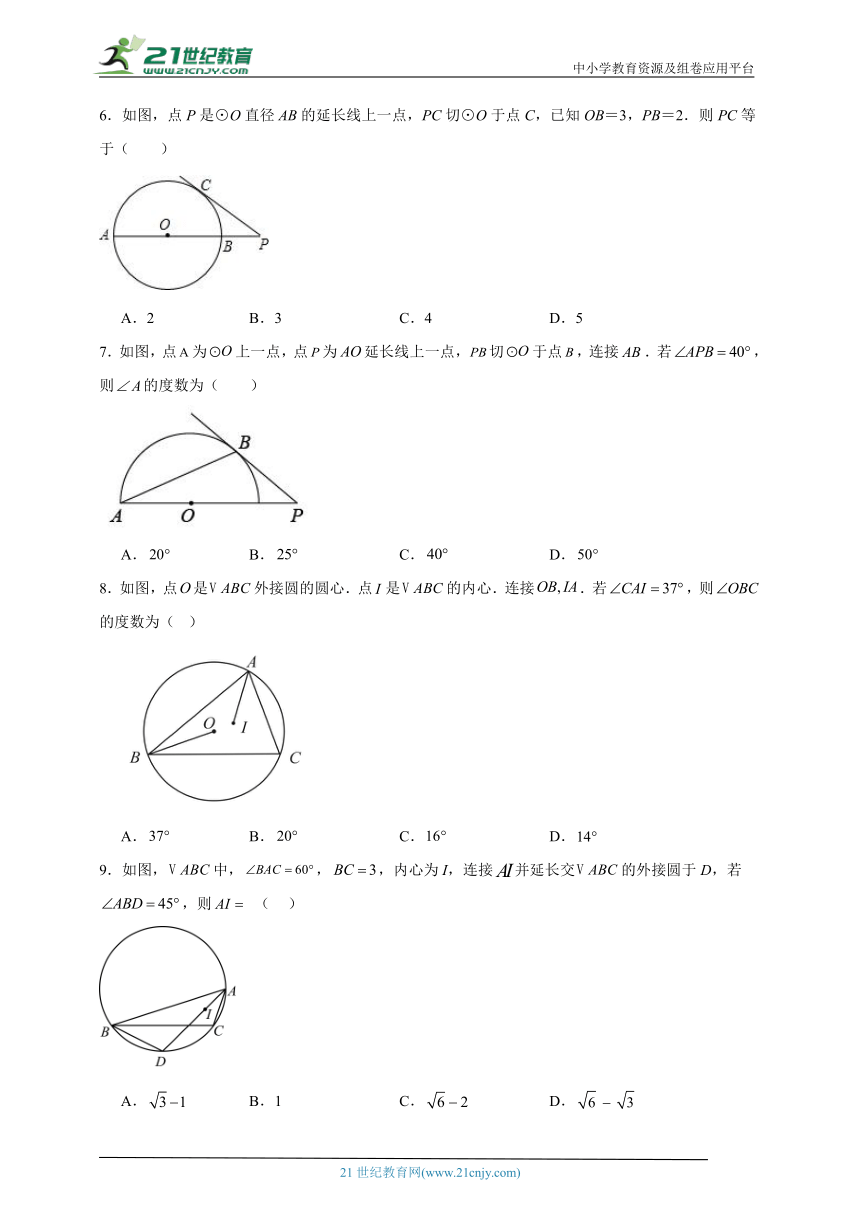
6.如图,点P是⊙O直径AB的延长线上一点,PC切⊙O于点C,已知OB=3,PB=2.则PC等于( )
A.2 B.3 C.4 D.5
7.如图,点为上一点,点为延长线上一点,切于点,连接.若,则的度数为( )
A. B. C. D.
8.如图,点是外接圆的圆心.点是的内心.连接.若,则的度数为( )
A. B. C. D.
9.如图,中,,,内心为I,连接并延长交的外接圆于D,若,则 ( )
A. B.1 C. D.
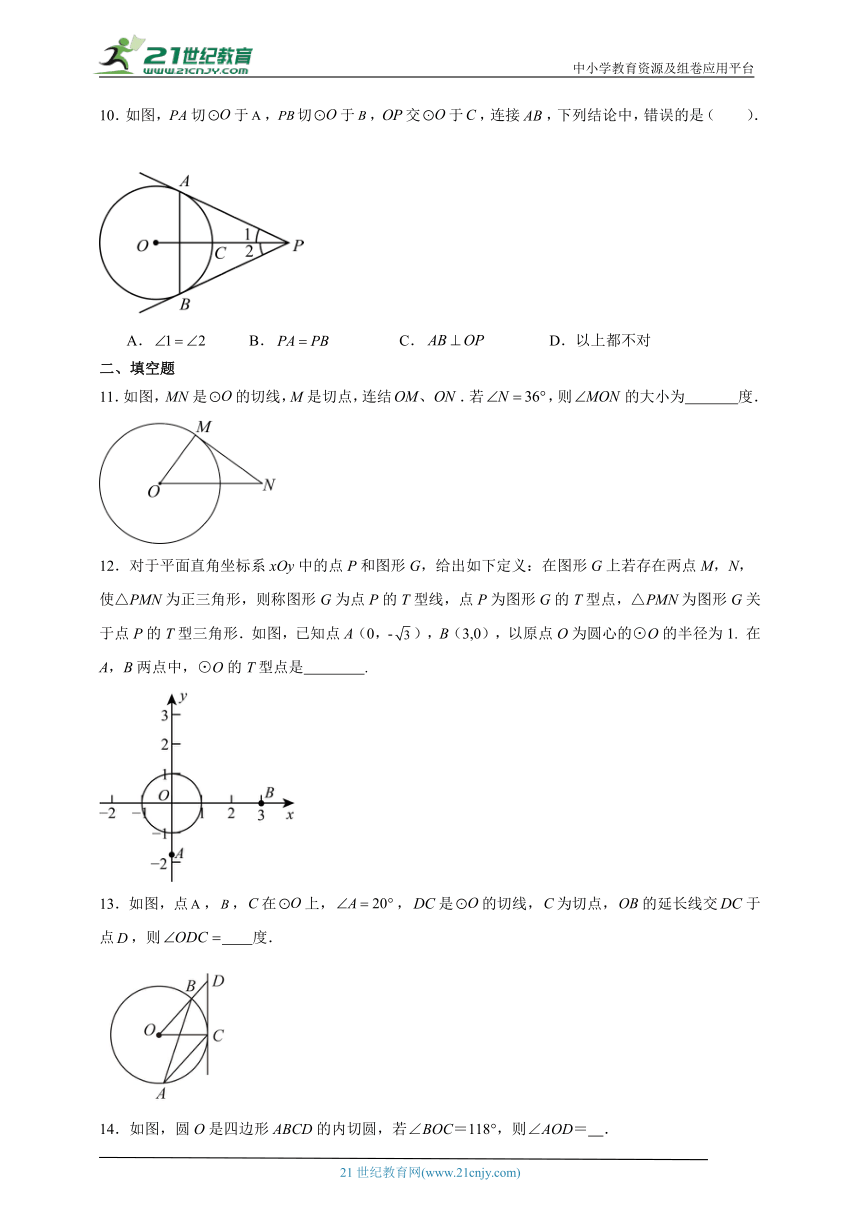
10.如图,切于,切于,交于,连接,下列结论中,错误的是( ).
A. B. C. D.以上都不对
二、填空题
11.如图,是的切线,M是切点,连结.若,则的大小为 度.
12.对于平面直角坐标系xOy中的点P和图形G,给出如下定义:在图形G上若存在两点M,N,使△PMN为正三角形,则称图形G为点P的T型线,点P为图形G的T型点,△PMN为图形G关于点P的T型三角形.如图,已知点A(0,-),B(3,0),以原点O为圆心的⊙O的半径为1. 在A,B两点中,⊙O的T型点是 .
13.如图,点,,在上,,是的切线,为切点,的延长线交于点,则 度.
14.如图,圆O是四边形ABCD的内切圆,若∠BOC=118°,则∠AOD= .
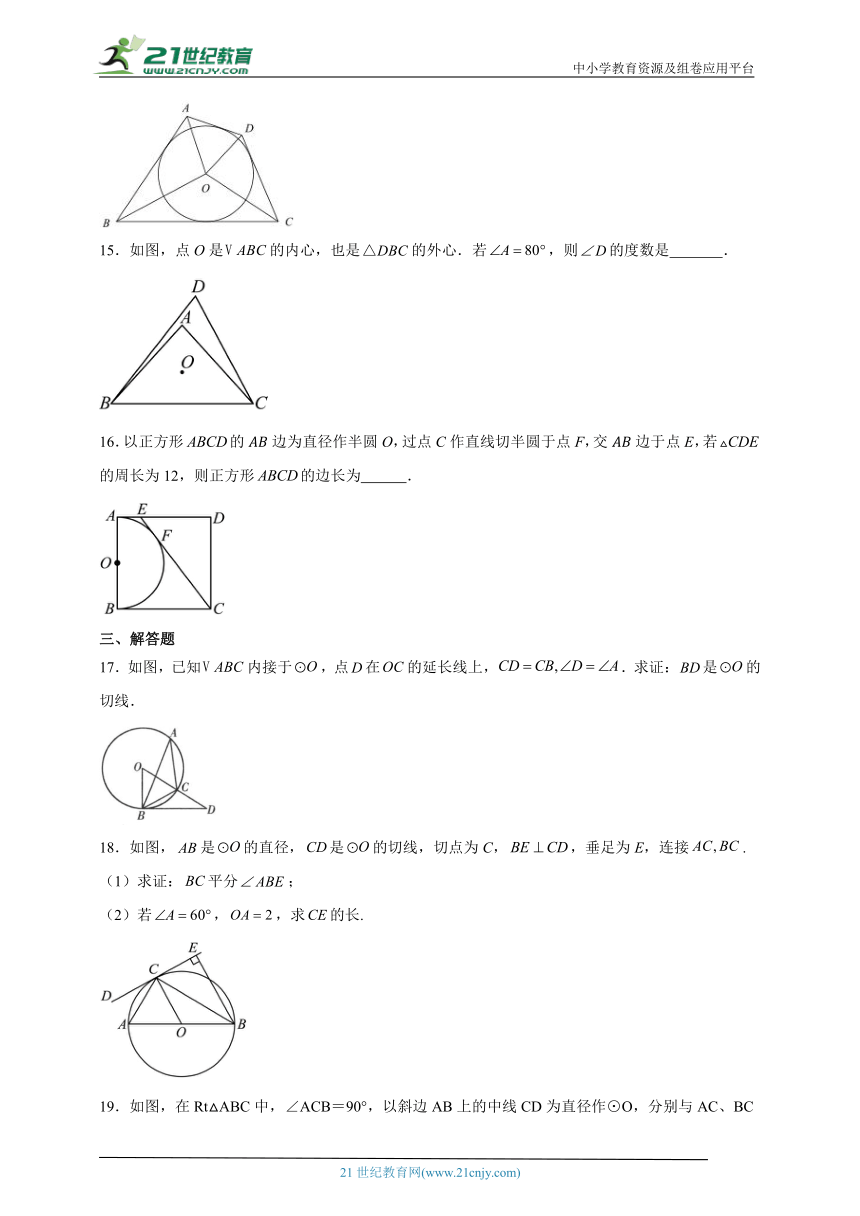
15.如图,点O是的内心,也是的外心.若,则的度数是 .
16.以正方形的边为直径作半圆O,过点C作直线切半圆于点F,交边于点E,若的周长为12,则正方形的边长为 .
三、解答题
17.如图,已知内接于,点在的延长线上,.求证:是的切线.
18.如图,是的直径,是的切线,切点为C,,垂足为E,连接.
(1)求证:平分;
(2)若,,求的长.
19.如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC相交于点M、N.
(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;
(2)连接MD,求证:MD=NB.
20.如图,⊙O是GDP的内切圆,切点分别为A、B、H,切线EF与⊙O相切于点C,分别交PA、PB于点E、F.
(1)若△PEF的周长为12,求线段PA的长;
(2)若∠G=90°,GD=3,GP=4,求⊙O半径.
21.如图,已知:四边形是的外切四边形,,,,分别是切点,求证:.
参考答案:
1.C
解:∵的半径为,点是直线上的三点,的长度分别是、、,
∴圆心到直线的距离必定小于半径,
∴直线与相交,
2.D
解:∵是的切线,
∴,
∴,
∵,
∴,
∴,
∴,即.
3.B
解:连接,
切于,
,
,
,
.
4.B
解:由是的两条切线,
∴为的平分线,
∵,
∴,且,
∴为直角三角形,且,
∴,
∴的半径为.
5.C
连接OD,如图,
∵DE∥AC,
∴∠E=∠BAC=40°,
∵DE为切线,
∴OD⊥DE,
∴∠DOE=90°-40°=50°,
∵∠BOC=2∠A=80°.
∴∠COD=80°+50°=130°,
∵OC=OD,
∴∠OCD=∠ODC=(180°-130°)=25°.
6.C
解:连接OC,
∵PC为⊙O的切线,
∴,
∵OB=OC=3,PB=2,
∴,
∴.
7.B
解:连接,
切于点,
,
,
,
,
,
,
,
.
8.C
如图,连接,
∵点是的内心,
∴平分,
∵,
∴,
∵点是外接圆的圆心,
∴,
∵,
∴,
9.D
解:如图,设的外接圆的圆心为O,连接,,,,
在中,,,内心为I,
∴平分,
∴,
∴,
∵,
∴是等边三角形,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∵,,
∵I是的内心,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
10.D
连接,,如图,
∵切于,切于,
∴,即是等腰三角形,
∵,,
∴,
∴,即平分,
∴,即A、B、C三项都正确,
11.54
解∶∵是的切线,是切点,
∴,
∴
故答案为∶54.
12.点A
(1)如图,
∵JK=2,OJ=OK,AO⊥JK,
∴AJ==2,同理可得:AK=2,
∴△AJK为正三角形,
同理可得△AMN为正三角形,
故点A为⊙O的T型点,
故填:点A.
13.50
解:,
,
是的切线,为切点,
,
,
故答案为:50.
14.62°
解:∵圆O是四边形ABCD的内切圆,
∴OA平分ABC,OC平分∠BCD,OD平分∠ADC,OA平分∠BAD,
∴∠1=∠ABC,∠2=∠BCD,∠3=∠ADC,∠4=∠BAD,
∵∠1+∠2=180°﹣∠BOC=180°﹣118°=62°,
∴∠ABC+∠BCD=2(∠1+∠2)=2×62°=124°,
∵∠BAD+∠ADC=360°﹣(∠ABC+∠BCD)=360°﹣124°=236°,
∴∠3+∠4=(∠BAD+∠ADC)=×236°=118°,
∴∠AOD=180°﹣(∠3+∠4)=180°﹣118°=62°.
故答案为:62°.
15./65度
解:如图,连接,,
点是的内心,,
,是,的平分线,
,,
,
点也是的外心,
,
则的度数为.
故答案为:.
16.4
解:在正方形中,,,
∵与半圆相切于点,以正方形的边为直径作半圆O,
∴与半圆相切,
,
∵的周长为12,
,
,
∵,
正方形的边长为4.
故答案为:4.
17.证明见解析
证明:,
∴,
∴,
∵,
∴,
又,
∴,
∵,
∴,
∴,
∴,
∴BD是的切线.
18.(1)详见解析;(2)
(1)证明:∵是的切线,
∴,
又∵,
∴,
∴,
∴,
即平分;
(2)解:∵为的直径,
∴,
∵,
∴是等边三角形,.
∴,
∴
∵,且,
∴.
∴
19.(1)证明见解析;(2)证明见解析.
(1)如图,连接ON,
∵CD是Rt△ABC斜边AB上的中线,
∴AD=CD=DB,
∴∠DCB=∠DBC,
又∵OC=ON,∴∠DCB=∠ONC,
∴∠ONC=∠DBC,
∴ON∥AB,
∵NE是⊙O的切线,ON是⊙O的半径,
∴∠ONE=90°,
∴∠NEB=90°,即NE⊥AB;
(2)如图所示,由(1)可知ON∥AB,
∵OC=OD,∴
∴CN=NB=CB,
又∵CD是⊙O的直径,∴∠CMD=90°,
∵∠ACB=90°,
∴∠CMD+∠ACB=180°,∴MD//BC,
又∵D是AB的中点,∴MD=CB,
∴MD=NB.
20.(1)6;(2)1
解:(1)由题意得,AP,BP,EF都是圆O的切线,
∴由切线长定理可得,,,
∵△PEF的周长为12,
∴,
∴;
(2)如图所示,连接OA、OB、OH、OP、OD、OG,设圆的半径为r,
∴OA=OB=OH=r,
由切线的性质可得OA⊥PD,OB⊥PG,OH⊥DG,
∴
,
∵∠G=90°,GD=3,GP=4,
∴,,
∴即,
∴,
∴⊙O的半径为1.
21.见详解
根据切线长定理可得:,,,,
∴,,
∴,,
∵,,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.2.2 直线和圆的位置关系 同步练
2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.的半径为,点是直线上的三点,的长度分别是、、,则直线与的位置关系是: ( )
A.相离 B.相切 C.相交 D.不能确定
2.如图,是的切线,连接并延长交于点C.若,则的度数是( )
A. B. C. D.
3.如图,切于,的延长线交于,若,则的度数是
A.72° B.63° C.54° D.36°
4.如图,是的两条切线, 是切点,若,则的半径等于( )
A. B.1 C.2 D.
5.如图,AB是⊙O的直径,弦CD与AB相交,连接CO,过点D作⊙O的切线,与AB的延长线交于点E,若DE∥AC,∠BAC=40°,则∠OCD的度数为( )
A.65° B.30° C.25° D.20°
6.如图,点P是⊙O直径AB的延长线上一点,PC切⊙O于点C,已知OB=3,PB=2.则PC等于( )
A.2 B.3 C.4 D.5
7.如图,点为上一点,点为延长线上一点,切于点,连接.若,则的度数为( )
A. B. C. D.
8.如图,点是外接圆的圆心.点是的内心.连接.若,则的度数为( )
A. B. C. D.
9.如图,中,,,内心为I,连接并延长交的外接圆于D,若,则 ( )
A. B.1 C. D.
10.如图,切于,切于,交于,连接,下列结论中,错误的是( ).
A. B. C. D.以上都不对
二、填空题
11.如图,是的切线,M是切点,连结.若,则的大小为 度.
12.对于平面直角坐标系xOy中的点P和图形G,给出如下定义:在图形G上若存在两点M,N,使△PMN为正三角形,则称图形G为点P的T型线,点P为图形G的T型点,△PMN为图形G关于点P的T型三角形.如图,已知点A(0,-),B(3,0),以原点O为圆心的⊙O的半径为1. 在A,B两点中,⊙O的T型点是 .
13.如图,点,,在上,,是的切线,为切点,的延长线交于点,则 度.
14.如图,圆O是四边形ABCD的内切圆,若∠BOC=118°,则∠AOD= .
15.如图,点O是的内心,也是的外心.若,则的度数是 .
16.以正方形的边为直径作半圆O,过点C作直线切半圆于点F,交边于点E,若的周长为12,则正方形的边长为 .
三、解答题
17.如图,已知内接于,点在的延长线上,.求证:是的切线.
18.如图,是的直径,是的切线,切点为C,,垂足为E,连接.
(1)求证:平分;
(2)若,,求的长.
19.如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC相交于点M、N.
(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;
(2)连接MD,求证:MD=NB.
20.如图,⊙O是GDP的内切圆,切点分别为A、B、H,切线EF与⊙O相切于点C,分别交PA、PB于点E、F.
(1)若△PEF的周长为12,求线段PA的长;
(2)若∠G=90°,GD=3,GP=4,求⊙O半径.
21.如图,已知:四边形是的外切四边形,,,,分别是切点,求证:.
参考答案:
1.C
解:∵的半径为,点是直线上的三点,的长度分别是、、,
∴圆心到直线的距离必定小于半径,
∴直线与相交,
2.D
解:∵是的切线,
∴,
∴,
∵,
∴,
∴,
∴,即.
3.B
解:连接,
切于,
,
,
,
.
4.B
解:由是的两条切线,
∴为的平分线,
∵,
∴,且,
∴为直角三角形,且,
∴,
∴的半径为.
5.C
连接OD,如图,
∵DE∥AC,
∴∠E=∠BAC=40°,
∵DE为切线,
∴OD⊥DE,
∴∠DOE=90°-40°=50°,
∵∠BOC=2∠A=80°.
∴∠COD=80°+50°=130°,
∵OC=OD,
∴∠OCD=∠ODC=(180°-130°)=25°.
6.C
解:连接OC,
∵PC为⊙O的切线,
∴,
∵OB=OC=3,PB=2,
∴,
∴.
7.B
解:连接,
切于点,
,
,
,
,
,
,
,
.
8.C
如图,连接,
∵点是的内心,
∴平分,
∵,
∴,
∵点是外接圆的圆心,
∴,
∵,
∴,
9.D
解:如图,设的外接圆的圆心为O,连接,,,,
在中,,,内心为I,
∴平分,
∴,
∴,
∵,
∴是等边三角形,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∵,,
∵I是的内心,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
10.D
连接,,如图,
∵切于,切于,
∴,即是等腰三角形,
∵,,
∴,
∴,即平分,
∴,即A、B、C三项都正确,
11.54
解∶∵是的切线,是切点,
∴,
∴
故答案为∶54.
12.点A
(1)如图,
∵JK=2,OJ=OK,AO⊥JK,
∴AJ==2,同理可得:AK=2,
∴△AJK为正三角形,
同理可得△AMN为正三角形,
故点A为⊙O的T型点,
故填:点A.
13.50
解:,
,
是的切线,为切点,
,
,
故答案为:50.
14.62°
解:∵圆O是四边形ABCD的内切圆,
∴OA平分ABC,OC平分∠BCD,OD平分∠ADC,OA平分∠BAD,
∴∠1=∠ABC,∠2=∠BCD,∠3=∠ADC,∠4=∠BAD,
∵∠1+∠2=180°﹣∠BOC=180°﹣118°=62°,
∴∠ABC+∠BCD=2(∠1+∠2)=2×62°=124°,
∵∠BAD+∠ADC=360°﹣(∠ABC+∠BCD)=360°﹣124°=236°,
∴∠3+∠4=(∠BAD+∠ADC)=×236°=118°,
∴∠AOD=180°﹣(∠3+∠4)=180°﹣118°=62°.
故答案为:62°.
15./65度
解:如图,连接,,
点是的内心,,
,是,的平分线,
,,
,
点也是的外心,
,
则的度数为.
故答案为:.
16.4
解:在正方形中,,,
∵与半圆相切于点,以正方形的边为直径作半圆O,
∴与半圆相切,
,
∵的周长为12,
,
,
∵,
正方形的边长为4.
故答案为:4.
17.证明见解析
证明:,
∴,
∴,
∵,
∴,
又,
∴,
∵,
∴,
∴,
∴,
∴BD是的切线.
18.(1)详见解析;(2)
(1)证明:∵是的切线,
∴,
又∵,
∴,
∴,
∴,
即平分;
(2)解:∵为的直径,
∴,
∵,
∴是等边三角形,.
∴,
∴
∵,且,
∴.
∴
19.(1)证明见解析;(2)证明见解析.
(1)如图,连接ON,
∵CD是Rt△ABC斜边AB上的中线,
∴AD=CD=DB,
∴∠DCB=∠DBC,
又∵OC=ON,∴∠DCB=∠ONC,
∴∠ONC=∠DBC,
∴ON∥AB,
∵NE是⊙O的切线,ON是⊙O的半径,
∴∠ONE=90°,
∴∠NEB=90°,即NE⊥AB;
(2)如图所示,由(1)可知ON∥AB,
∵OC=OD,∴
∴CN=NB=CB,
又∵CD是⊙O的直径,∴∠CMD=90°,
∵∠ACB=90°,
∴∠CMD+∠ACB=180°,∴MD//BC,
又∵D是AB的中点,∴MD=CB,
∴MD=NB.
20.(1)6;(2)1
解:(1)由题意得,AP,BP,EF都是圆O的切线,
∴由切线长定理可得,,,
∵△PEF的周长为12,
∴,
∴;
(2)如图所示,连接OA、OB、OH、OP、OD、OG,设圆的半径为r,
∴OA=OB=OH=r,
由切线的性质可得OA⊥PD,OB⊥PG,OH⊥DG,
∴
,
∵∠G=90°,GD=3,GP=4,
∴,,
∴即,
∴,
∴⊙O的半径为1.
21.见详解
根据切线长定理可得:,,,,
∴,,
∴,,
∵,,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
