24.3 正多边形和圆 同步练 2024--2025学年上学期初中数学人教版九年级上册
文档属性
| 名称 | 24.3 正多边形和圆 同步练 2024--2025学年上学期初中数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 761.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.3 正多边形和圆 同步练
2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.如图,紫荆花绕它的旋转中心,按下列角度旋转,能与其自身重合的是( )
A. B. C. D.
2.若一个圆内接正多边形的中心角是60°,则这个正多边形是( )
A.正八边形 B.正七边形 C.正六边形 D.正五边形
3.一把直尺放在正六边形上,其中 点、 点分别对应刻度, 则 的长是 ( )
A. B. C. D.
4.每一片雪花各顶点连接其外形就是正六边形.若绕这个正六边形的中心旋转至和原图形重合,至少需要旋转( )
A. B. C. D.
5.如图是一个正八边形,则它( )
A.只是轴对称图形 B.只是中心对称图形
C.既是轴对称图形,也是中心对称图形 D.既不是轴对称图形,也不是中心对称图形
6.若正多边形的一个外角为,则这个正多边形的中心角的度数是( )
A. B. C. D.
7.如图,已知的内接正方形的边长为1,则的半径为( )
A. B. C.1 D.
8.正六边形的边心距为,则该正六边形的边长是( )
A. B.2 C.3 D.2
9.如图所示,的内接多边形的周长为3,的外切多边形的周长为,则下列各数中与此圆的周长最接近的是( )
A. B. C. D.
10.小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
(1)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;
(2)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是( )
A. B.
C. D.
二、填空题
11.正九边形的中心角等于 度.
12.边长为3的等边三角形内接于,则的半径为 .
13.已知⊙O是正方形ABCD与正三角形EFG的外接圆,正方形的边长为a,则正三角形EFG的边长为 .
14.已知正六边形ABCDEF内接于⊙O,图中阴影部分的面积为,则⊙O的半径为 .
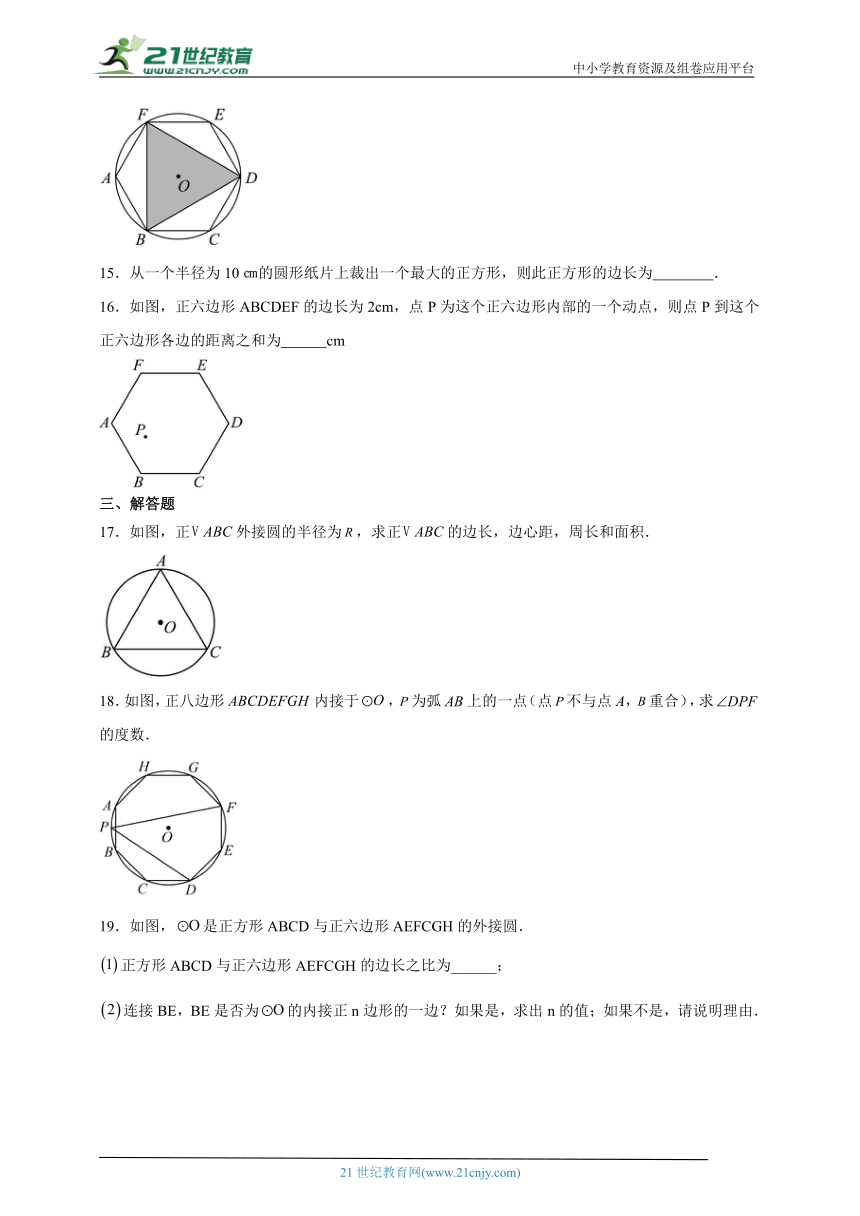
15.从一个半径为10㎝的圆形纸片上裁出一个最大的正方形,则此正方形的边长为 .
16.如图,正六边形ABCDEF的边长为2cm,点P为这个正六边形内部的一个动点,则点P到这个正六边形各边的距离之和为 cm
三、解答题
17.如图,正外接圆的半径为,求正的边长,边心距,周长和面积.
18.如图,正八边形内接于,为弧上的一点(点不与点A,重合),求的度数.
19.如图,是正方形ABCD与正六边形AEFCGH的外接圆.
正方形ABCD与正六边形AEFCGH的边长之比为______;
连接BE,BE是否为的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.
参考答案:
1.C
解:由题意得:正五边形的边所对的圆心角为,
∴该紫荆花绕它的旋转中心进行旋转时,只需满足旋转角度是的整数倍即可;
2.C
解:,
即这个多边形的边数是6,是正六边形.
3.C
解:取中点,连接,可知点为正六边形的中心,
∴,,
∴为等边三角形,
∴,
∵点、点分别对应刻度,
∴,
∴,
∵六边形是正六边形,
∴,
4.D
解:正六边形的中心角的度数为,
∴绕这个正六边形的中心旋转至和原图形重合,至少需要旋转;
5.C
解:正八边形既是轴对称图形,也是中心对称图形.
6.C
∵正多边形的一个外角为,
∴正多边形的边数为,
∴这个正多边形的中心角的度数是,
7.B
解:连接,如图所示,
∵的内接正方形的边长为1,
∴,
在中,,
∴.
8.B
如图:
∵正六边形的边心距为,
∴OB=,AB=OA,
∵OA2=AB2+OB2,
∴OA2=(OA)2+()2,
解得OA=2.
9.C
解:圆外切多边形的周长大于圆周长,圆内接多边形的周长小于圆周长,
圆的内接多边形周长为3,外切多边形周长为3.4,所以圆周长在3与3.4之间,
,
圆的周长,
只有C选项满足条件.
10.C
解:如图,连接BM,
根据题意得:OB=OA=1,AD⊥OB,BM=DM,
∵OA的垂直平分线交OA于点M,∴OM=AM=OA=,
∴.∴DM=,
∴OD=DM-OM=,
∴,
11.40
解:正九边形的中心角等于:.
故答案是:.
12.
解:作于D点,连接,
∵等边三角形内接于,,
∴,,
∴,
∴,即,
∴,
∴的半径为.
故答案为:.
13.
解:连接AC、OE、OF,作OM⊥EF于M,
∵四边形ABCD是正方形,
∴AB=BC=a,∠ABC=90°,
∴AC是直径,AC=a,
∴OE=OF=a,
∵OM⊥EF,
∴EM=MF,
∵△EFG是等边三角形,
∴∠GEF=60°,
在Rt△OME中,
∵OE=a,∠OEM=∠GEF=30°,
∴EM=OE=a,
∴EF=a.
故答案为a.
14.4.
阴影部分是一个正三角形,连接DO并延长,交BF于点G.
设边长是a,
则面积是,
得到=12,
解得a=4,
则DG=BD sin60°=4×=6
因而半径OD=DG=6×=4.
15.cm
解:设该正方形的边长为x,则:
要想裁出一块面积最大的正方形,需要正方形边长最长,所以正方形的四个顶点在圆周上,
如下图所示:
连接OA,过O作OE⊥AD交AD与E,则:
在Rt△AEO中,由勾股定理得:
,
解得:,
∴该正方形的边长为.
故答案为.
16.6
如图所示,过P作PH⊥BC于H,
根据正六边形的性质可知,∠BPC=60°,
即∠BPH=∠BPC=×60°=30°,BH=BC=×2=1cm;
∴PH=
∴正六边形各边的距离之和=6PH=6×=6cm.
17.边心距,边长为,周长是,面积是.
解:如图:连接,延长交于D,
∵正外接圆是,
∴,
∴边心距,
由勾股定理得:,
∴三角形边长为,,
∴的周长是;
的面积是.
18.
解:如图,连接、、,
∵八边形是正八边形,
∴,
∴,
∴.
19.(1);(2)是,n=12.
()连接、、,
设半径为,
,,
是等腰直角三角形,,
是等边三角形,,
∴.
()若是,则,
又∵,∴,,
故是⊙内接正十二边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.3 正多边形和圆 同步练
2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.如图,紫荆花绕它的旋转中心,按下列角度旋转,能与其自身重合的是( )
A. B. C. D.
2.若一个圆内接正多边形的中心角是60°,则这个正多边形是( )
A.正八边形 B.正七边形 C.正六边形 D.正五边形
3.一把直尺放在正六边形上,其中 点、 点分别对应刻度, 则 的长是 ( )
A. B. C. D.
4.每一片雪花各顶点连接其外形就是正六边形.若绕这个正六边形的中心旋转至和原图形重合,至少需要旋转( )
A. B. C. D.
5.如图是一个正八边形,则它( )
A.只是轴对称图形 B.只是中心对称图形
C.既是轴对称图形,也是中心对称图形 D.既不是轴对称图形,也不是中心对称图形
6.若正多边形的一个外角为,则这个正多边形的中心角的度数是( )
A. B. C. D.
7.如图,已知的内接正方形的边长为1,则的半径为( )
A. B. C.1 D.
8.正六边形的边心距为,则该正六边形的边长是( )
A. B.2 C.3 D.2
9.如图所示,的内接多边形的周长为3,的外切多边形的周长为,则下列各数中与此圆的周长最接近的是( )
A. B. C. D.
10.小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
(1)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;
(2)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是( )
A. B.
C. D.
二、填空题
11.正九边形的中心角等于 度.
12.边长为3的等边三角形内接于,则的半径为 .
13.已知⊙O是正方形ABCD与正三角形EFG的外接圆,正方形的边长为a,则正三角形EFG的边长为 .
14.已知正六边形ABCDEF内接于⊙O,图中阴影部分的面积为,则⊙O的半径为 .
15.从一个半径为10㎝的圆形纸片上裁出一个最大的正方形,则此正方形的边长为 .
16.如图,正六边形ABCDEF的边长为2cm,点P为这个正六边形内部的一个动点,则点P到这个正六边形各边的距离之和为 cm
三、解答题
17.如图,正外接圆的半径为,求正的边长,边心距,周长和面积.
18.如图,正八边形内接于,为弧上的一点(点不与点A,重合),求的度数.
19.如图,是正方形ABCD与正六边形AEFCGH的外接圆.
正方形ABCD与正六边形AEFCGH的边长之比为______;
连接BE,BE是否为的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.
参考答案:
1.C
解:由题意得:正五边形的边所对的圆心角为,
∴该紫荆花绕它的旋转中心进行旋转时,只需满足旋转角度是的整数倍即可;
2.C
解:,
即这个多边形的边数是6,是正六边形.
3.C
解:取中点,连接,可知点为正六边形的中心,
∴,,
∴为等边三角形,
∴,
∵点、点分别对应刻度,
∴,
∴,
∵六边形是正六边形,
∴,
4.D
解:正六边形的中心角的度数为,
∴绕这个正六边形的中心旋转至和原图形重合,至少需要旋转;
5.C
解:正八边形既是轴对称图形,也是中心对称图形.
6.C
∵正多边形的一个外角为,
∴正多边形的边数为,
∴这个正多边形的中心角的度数是,
7.B
解:连接,如图所示,
∵的内接正方形的边长为1,
∴,
在中,,
∴.
8.B
如图:
∵正六边形的边心距为,
∴OB=,AB=OA,
∵OA2=AB2+OB2,
∴OA2=(OA)2+()2,
解得OA=2.
9.C
解:圆外切多边形的周长大于圆周长,圆内接多边形的周长小于圆周长,
圆的内接多边形周长为3,外切多边形周长为3.4,所以圆周长在3与3.4之间,
,
圆的周长,
只有C选项满足条件.
10.C
解:如图,连接BM,
根据题意得:OB=OA=1,AD⊥OB,BM=DM,
∵OA的垂直平分线交OA于点M,∴OM=AM=OA=,
∴.∴DM=,
∴OD=DM-OM=,
∴,
11.40
解:正九边形的中心角等于:.
故答案是:.
12.
解:作于D点,连接,
∵等边三角形内接于,,
∴,,
∴,
∴,即,
∴,
∴的半径为.
故答案为:.
13.
解:连接AC、OE、OF,作OM⊥EF于M,
∵四边形ABCD是正方形,
∴AB=BC=a,∠ABC=90°,
∴AC是直径,AC=a,
∴OE=OF=a,
∵OM⊥EF,
∴EM=MF,
∵△EFG是等边三角形,
∴∠GEF=60°,
在Rt△OME中,
∵OE=a,∠OEM=∠GEF=30°,
∴EM=OE=a,
∴EF=a.
故答案为a.
14.4.
阴影部分是一个正三角形,连接DO并延长,交BF于点G.
设边长是a,
则面积是,
得到=12,
解得a=4,
则DG=BD sin60°=4×=6
因而半径OD=DG=6×=4.
15.cm
解:设该正方形的边长为x,则:
要想裁出一块面积最大的正方形,需要正方形边长最长,所以正方形的四个顶点在圆周上,
如下图所示:
连接OA,过O作OE⊥AD交AD与E,则:
在Rt△AEO中,由勾股定理得:
,
解得:,
∴该正方形的边长为.
故答案为.
16.6
如图所示,过P作PH⊥BC于H,
根据正六边形的性质可知,∠BPC=60°,
即∠BPH=∠BPC=×60°=30°,BH=BC=×2=1cm;
∴PH=
∴正六边形各边的距离之和=6PH=6×=6cm.
17.边心距,边长为,周长是,面积是.
解:如图:连接,延长交于D,
∵正外接圆是,
∴,
∴边心距,
由勾股定理得:,
∴三角形边长为,,
∴的周长是;
的面积是.
18.
解:如图,连接、、,
∵八边形是正八边形,
∴,
∴,
∴.
19.(1);(2)是,n=12.
()连接、、,
设半径为,
,,
是等腰直角三角形,,
是等边三角形,,
∴.
()若是,则,
又∵,∴,,
故是⊙内接正十二边形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
