24.4 弧长和扇形面积 同步练 2024--2025学年上学期初中数学人教版九年级上册
文档属性
| 名称 | 24.4 弧长和扇形面积 同步练 2024--2025学年上学期初中数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 932.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-18 19:02:22 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.4 弧长和扇形面积 同步练
2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.将一把折扇展开,可抽象成一个扇形,若该扇形的半径为2,弧长为,则扇形的圆心角大小为( )
A. B. C. D.
2.传统服饰日益受到关注,如图①为明清时期女子主要裙式之一的马面裙,如图②马面裙可以近似地看作扇形的一部分,其中的长度为米,裙长米,圆心角,则的长为( )
A.1米 B.米 C.2米 D.米
3.如图,是的直径,,则( )
A. B. C. D.
4.某校开展研学活动,其中有“列队训练”的项目.我们以“向右转”为例研究其中蕴含的数学知识,如图,把右脚鞋底抽象成一条线段,忽略鞋底的摩擦、弹性等误差.“向右转”时,以鞋跟O为圆心,顺时针旋转得线段.若某同学右脚鞋底长,那么鞋尖A在“向右转”的运动中路径长是( )
A. B. C. D.
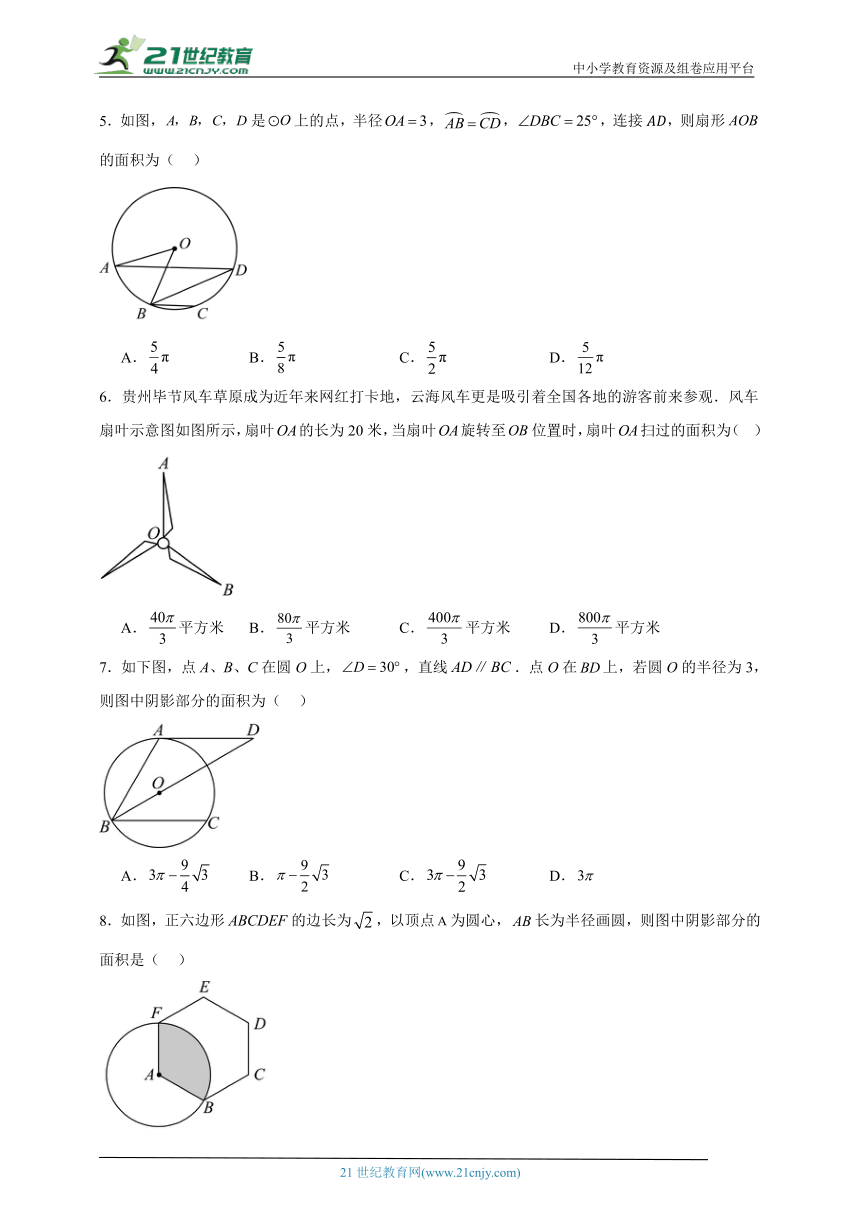
5.如图,是上的点,半径,,,连接,则扇形的面积为( )
A. B. C. D.
6.贵州毕节风车草原成为近年来网红打卡地,云海风车更是吸引着全国各地的游客前来参观.风车扇叶示意图如图所示,扇叶的长为20米,当扇叶旋转至位置时,扇叶扫过的面积为( )
A.平方米 B.平方米 C.平方米 D.平方米
7.如下图,点A、B、C在圆O上,,直线.点O在上,若圆O的半径为3,则图中阴影部分的面积为( )
A. B. C. D.
8.如图,正六边形的边长为,以顶点为圆心,长为半径画圆,则图中阴影部分的面积是( )
A. B. C. D.
9.如图,已知圆锥的母线长为6,圆锥的底面半径与母线的比为,则该圆锥的侧面积是( )
A. B. C. D.
10.为了拉动乡村经济振兴,某村设立了一个草帽手工作坊,让留守的老人也能赚钱,其制作工艺中用固定规格的扇形草毡围成一个底面周长为,侧面积为的圆锥形草帽,则制作工艺中所使用扇形草毡的圆心角为( )
A. B. C. D.
二、填空题
11.如图所示是一个侧面积为的圆锥形冰淇淋外壳(不计厚度),若其底面圆的半径为,则它的母线长为 cm.
12.已知圆锥的底面半径是1,高是,则该圆锥的侧面展开图的圆心角是 度.
13.如图,从一块边长为2的等边三角形卡纸上剪下一个面积最大的扇形,并将其围成一个圆锥,则圆锥的底面圆的半径是 .
14.如图①, 是的半径,弦垂直平分,垂足为点,,连接,,将图中阴影部分的扇形剪下围成一个圆锥的侧面(如图,则圆锥的底面圆半径是 cm.
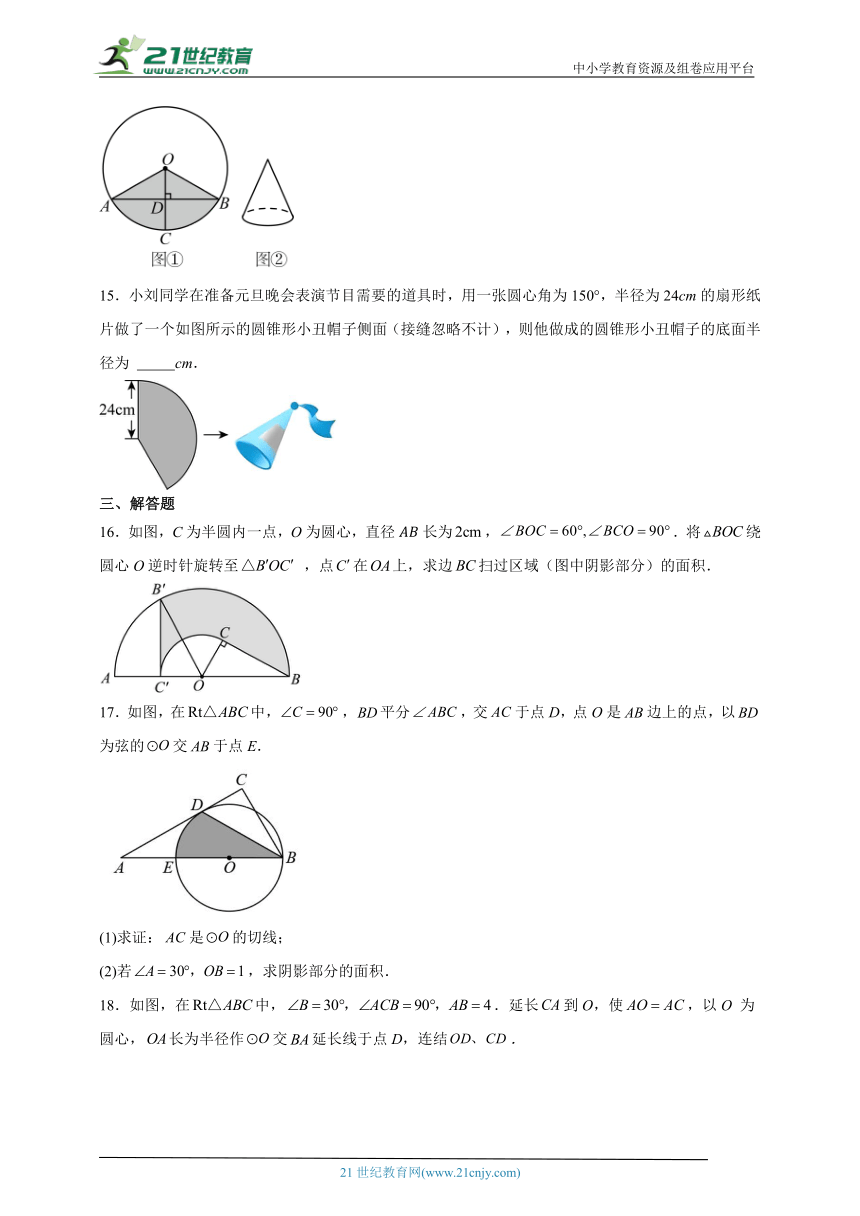
15.小刘同学在准备元旦晚会表演节目需要的道具时,用一张圆心角为150°,半径为24cm的扇形纸片做了一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),则他做成的圆锥形小丑帽子的底面半径为 cm.
三、解答题
16.如图,C为半圆内一点,O为圆心,直径长为,.将绕圆心O逆时针旋转至 ,点在上,求边扫过区域(图中阴影部分)的面积.
17.如图,在中,,平分,交于点D,点O是边上的点,以为弦的交于点E.
(1)求证:是的切线;
(2)若,求阴影部分的面积.
18.如图,在中,.延长到O,使,以O 为圆心,长为半径作交延长线于点D,连结.
(1)求扇形的面积.
(2)判断所在直线与的位置关系,并说明理由.
19.如图,在中,,以为直径的交于点E.求的长.
参考答案:
1.D
已知,,
,
,
解得.
2.B
解:由题意知,,
解得,
∵裙长为米,
∴米,
3.D
解:连接,如图:
设,则,
则的长为,的长为,
∵,
即,
整理得:,
解得:,
即,,
∵,
∴.
4.A
解:依题意可知:鞋尖A在 “向右转”的运动中路径长是一段弧长,其半径是,弧的圆心角为,
∴ 鞋尖A在“向右转”的运动中路径长.
5.A
解:连接,则,
∵,
∴,
∴,
6.C
解:由题意,扇叶扫过的图形为扇形,且,半径米,
∴扇叶扫过的面积为平方米,
7.A
解:连接,作,则:,
∴,
∵,直线,
∴,
∴,
∵,,
∴,
∴,
∴阴影部分的面积为;
8.B
解:六边形是正六边形,
,,
,
9.C
解:∵圆锥的底面半径与母线的比为,母线长为6,
∴圆锥的底面半径,
∴该圆锥的侧面积.
10.B
解:设扇形的半径为r,则,
解得:;
设扇形圆心角度数为n度,则,
解得:,
即扇形圆心角为;
11.12
解:底面圆的半径为,
底面圆的周长为,即圆锥侧面展开图扇形的弧长为,
设母线长为
∵侧面积为的圆锥形冰淇淋外壳
∴
故答案为:12
12.90
解:设圆锥的母线为a,根据勾股定理得, ,
设圆锥的侧面展开图的圆心角度数为 ,
根据题意得 ,解得 ,
即圆锥的侧面展开图的圆心角度数为.
故答案为90.
13./
解:连接,由题意得,
是边长为2的等边三角形,
∴
,
扇形的弧长为,
圆锥的底面圆的半径是.
故答案为:.
14.2
解:弦垂直平分,
,
则,,
,
,
,
则,
扇形的弧长,即圆锥的底面周长为,
则,
解得,
故答案为:2
15.10
解:∵扇形半径为24cm,圆心角为150°,
∴扇形的弧长为cm,
设圆锥的底面半径为rcm,
则2πr=20π,
解得:r=10,
故答案为:10.
16.
解:如图可知,
∵,是由绕圆心O逆时针旋转得到,
∴,
∴,
∴,
又∵,
∴,
∴,
∴ ,,
.
17.(1)见解析
(2).
(1)证明:连接,
∵,
∴,
∵平分,
∴,
∴,
∴,
∴,
∴,
∵是半径,
∴是的切线;
(2)解:作于点F,则,
∵,
∴,
由(1)得,
∵,
∴,
∴,
∴,,
∴,
∴.
18.(1)
(2)所在直线与相切,见解析
(1)在中,,
∴,.
∴.
∵,
∴是等边三角形.
∴.
∴.
(2)所在直线与相切.
理由:∵是等边三角形,
∴.
∵,
∴.
∴.
∴,即.
∵为的半径,
∴所在直线与相切.
19.的长为π
解:连接,
在中,,
∴,
∴,
∵,
∴为等边三角形,
∴,
∴的长
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.4 弧长和扇形面积 同步练
2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.将一把折扇展开,可抽象成一个扇形,若该扇形的半径为2,弧长为,则扇形的圆心角大小为( )
A. B. C. D.
2.传统服饰日益受到关注,如图①为明清时期女子主要裙式之一的马面裙,如图②马面裙可以近似地看作扇形的一部分,其中的长度为米,裙长米,圆心角,则的长为( )
A.1米 B.米 C.2米 D.米
3.如图,是的直径,,则( )
A. B. C. D.
4.某校开展研学活动,其中有“列队训练”的项目.我们以“向右转”为例研究其中蕴含的数学知识,如图,把右脚鞋底抽象成一条线段,忽略鞋底的摩擦、弹性等误差.“向右转”时,以鞋跟O为圆心,顺时针旋转得线段.若某同学右脚鞋底长,那么鞋尖A在“向右转”的运动中路径长是( )
A. B. C. D.
5.如图,是上的点,半径,,,连接,则扇形的面积为( )
A. B. C. D.
6.贵州毕节风车草原成为近年来网红打卡地,云海风车更是吸引着全国各地的游客前来参观.风车扇叶示意图如图所示,扇叶的长为20米,当扇叶旋转至位置时,扇叶扫过的面积为( )
A.平方米 B.平方米 C.平方米 D.平方米
7.如下图,点A、B、C在圆O上,,直线.点O在上,若圆O的半径为3,则图中阴影部分的面积为( )
A. B. C. D.
8.如图,正六边形的边长为,以顶点为圆心,长为半径画圆,则图中阴影部分的面积是( )
A. B. C. D.
9.如图,已知圆锥的母线长为6,圆锥的底面半径与母线的比为,则该圆锥的侧面积是( )
A. B. C. D.
10.为了拉动乡村经济振兴,某村设立了一个草帽手工作坊,让留守的老人也能赚钱,其制作工艺中用固定规格的扇形草毡围成一个底面周长为,侧面积为的圆锥形草帽,则制作工艺中所使用扇形草毡的圆心角为( )
A. B. C. D.
二、填空题
11.如图所示是一个侧面积为的圆锥形冰淇淋外壳(不计厚度),若其底面圆的半径为,则它的母线长为 cm.
12.已知圆锥的底面半径是1,高是,则该圆锥的侧面展开图的圆心角是 度.
13.如图,从一块边长为2的等边三角形卡纸上剪下一个面积最大的扇形,并将其围成一个圆锥,则圆锥的底面圆的半径是 .
14.如图①, 是的半径,弦垂直平分,垂足为点,,连接,,将图中阴影部分的扇形剪下围成一个圆锥的侧面(如图,则圆锥的底面圆半径是 cm.
15.小刘同学在准备元旦晚会表演节目需要的道具时,用一张圆心角为150°,半径为24cm的扇形纸片做了一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),则他做成的圆锥形小丑帽子的底面半径为 cm.
三、解答题
16.如图,C为半圆内一点,O为圆心,直径长为,.将绕圆心O逆时针旋转至 ,点在上,求边扫过区域(图中阴影部分)的面积.
17.如图,在中,,平分,交于点D,点O是边上的点,以为弦的交于点E.
(1)求证:是的切线;
(2)若,求阴影部分的面积.
18.如图,在中,.延长到O,使,以O 为圆心,长为半径作交延长线于点D,连结.
(1)求扇形的面积.
(2)判断所在直线与的位置关系,并说明理由.
19.如图,在中,,以为直径的交于点E.求的长.
参考答案:
1.D
已知,,
,
,
解得.
2.B
解:由题意知,,
解得,
∵裙长为米,
∴米,
3.D
解:连接,如图:
设,则,
则的长为,的长为,
∵,
即,
整理得:,
解得:,
即,,
∵,
∴.
4.A
解:依题意可知:鞋尖A在 “向右转”的运动中路径长是一段弧长,其半径是,弧的圆心角为,
∴ 鞋尖A在“向右转”的运动中路径长.
5.A
解:连接,则,
∵,
∴,
∴,
6.C
解:由题意,扇叶扫过的图形为扇形,且,半径米,
∴扇叶扫过的面积为平方米,
7.A
解:连接,作,则:,
∴,
∵,直线,
∴,
∴,
∵,,
∴,
∴,
∴阴影部分的面积为;
8.B
解:六边形是正六边形,
,,
,
9.C
解:∵圆锥的底面半径与母线的比为,母线长为6,
∴圆锥的底面半径,
∴该圆锥的侧面积.
10.B
解:设扇形的半径为r,则,
解得:;
设扇形圆心角度数为n度,则,
解得:,
即扇形圆心角为;
11.12
解:底面圆的半径为,
底面圆的周长为,即圆锥侧面展开图扇形的弧长为,
设母线长为
∵侧面积为的圆锥形冰淇淋外壳
∴
故答案为:12
12.90
解:设圆锥的母线为a,根据勾股定理得, ,
设圆锥的侧面展开图的圆心角度数为 ,
根据题意得 ,解得 ,
即圆锥的侧面展开图的圆心角度数为.
故答案为90.
13./
解:连接,由题意得,
是边长为2的等边三角形,
∴
,
扇形的弧长为,
圆锥的底面圆的半径是.
故答案为:.
14.2
解:弦垂直平分,
,
则,,
,
,
,
则,
扇形的弧长,即圆锥的底面周长为,
则,
解得,
故答案为:2
15.10
解:∵扇形半径为24cm,圆心角为150°,
∴扇形的弧长为cm,
设圆锥的底面半径为rcm,
则2πr=20π,
解得:r=10,
故答案为:10.
16.
解:如图可知,
∵,是由绕圆心O逆时针旋转得到,
∴,
∴,
∴,
又∵,
∴,
∴,
∴ ,,
.
17.(1)见解析
(2).
(1)证明:连接,
∵,
∴,
∵平分,
∴,
∴,
∴,
∴,
∴,
∵是半径,
∴是的切线;
(2)解:作于点F,则,
∵,
∴,
由(1)得,
∵,
∴,
∴,
∴,,
∴,
∴.
18.(1)
(2)所在直线与相切,见解析
(1)在中,,
∴,.
∴.
∵,
∴是等边三角形.
∴.
∴.
(2)所在直线与相切.
理由:∵是等边三角形,
∴.
∵,
∴.
∴.
∴,即.
∵为的半径,
∴所在直线与相切.
19.的长为π
解:连接,
在中,,
∴,
∴,
∵,
∴为等边三角形,
∴,
∴的长
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
