第24章 圆 章末测试题 2024--2025学年上学期初中数学人教版九年级上册
文档属性
| 名称 | 第24章 圆 章末测试题 2024--2025学年上学期初中数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 618.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
圆 易错知识点单选 强化练
2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.如图,点A,B,C,D在上,,则的度数为( )
A. B. C. D.
2.已知的半径是,点在圆内,则的长( )
A.小于 B.等于
C.大于 D.等于
3.如图,A,B,C是上的三个点,如果,那么的度数是( )
A. B. C. D.
4.如图,四边形是的内接四边形,若,则的度数为( )
A. B. C. D.
5.如图,在直线l上有相距的两点A和O(点A在点O的右侧),以O为圆心作半径为的圆,过点A作直线.将以的速度向右移动(点O始终在直线l上),则与直线在( )秒时相切
A.3 B.4 C.3或4 D.3或
6.已知与的半径分别为和,若.则与的位置关系是
A.外离 B.相交 C.内切 D.外切
7.△ABC的外心在三角形的内部,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
8.如图,是的切线,为切点,交于点,若,,则的长为( )
A.5 B.7 C.8 D.13
9.如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为π cm2,则扇形圆心角的度数为( )
A.120° B.140° C.150° D.160°
10.如图是两个同心圆,大圆的直径AC固定不动,小圆的直径BD绕着圆心0旋转,BD与AC不在同一条直线上,在BD旋转过程中,下面说法正确的是( )
A.∠ADC的大小始终不变 B.四边形ABCD存在是矩形的情形
C.四边形ABCD的最大面积等于AC·BD. D.AD的最大值等于(AC+BD)
二、填空题
11.如图,A、B、C点在圆O上, 若∠ACB=36°, 则∠AOB= .
12.扇形的半径为2,圆心角为90°,则该扇形的面积(结果保留)为 .
13.若圆锥的底面圆半径为2,母线长为5,则该圆锥的侧面积是 .(结果保留)
14.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为 .
15.如图,内切于正方形,为圆心,作,其两边分别交,于点,,若,则的面积为 .
16.如图,已知是的内切圆,点是内心,若,则等于 .
17.如图,在中,,是的内切圆,三个切点分别为,,,若,,则的面积是 .
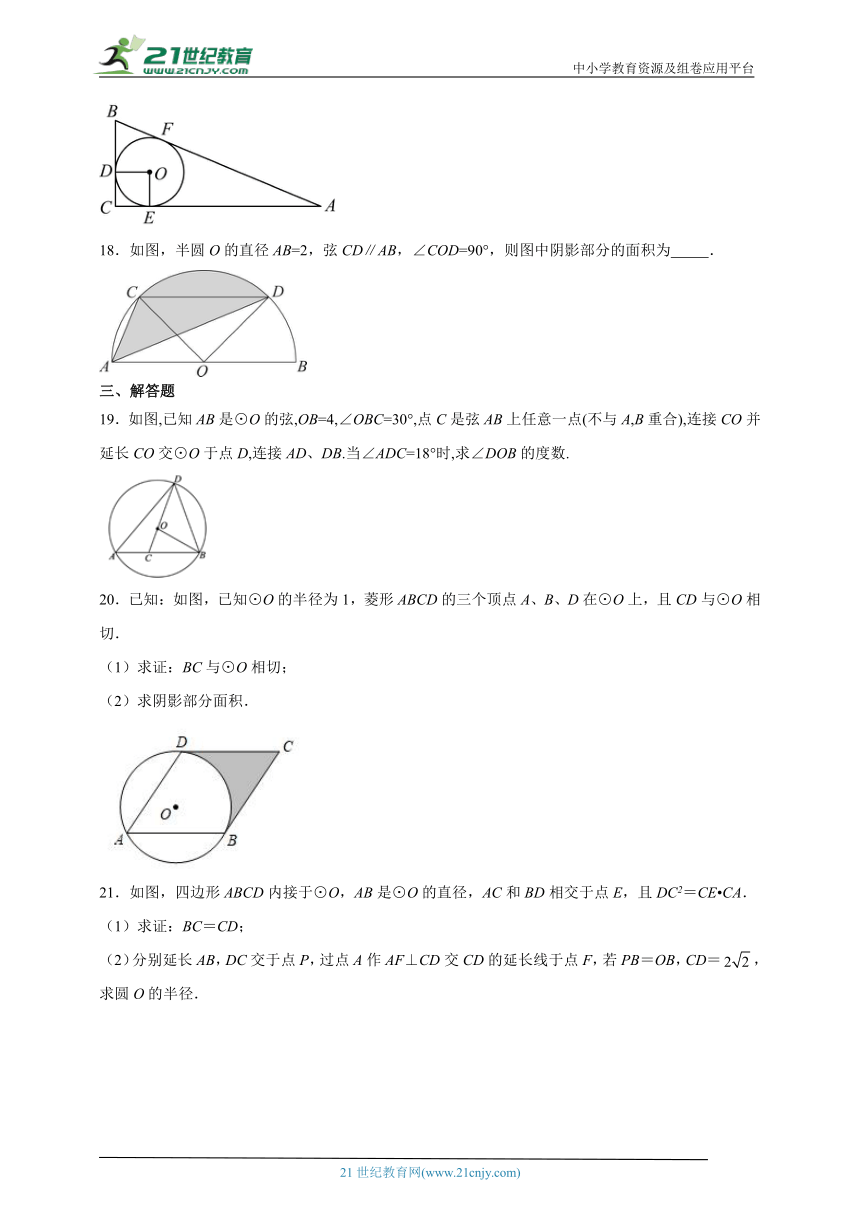
18.如图,半圆O的直径AB=2,弦CD∥AB,∠COD=90°,则图中阴影部分的面积为 .
三、解答题
19.如图,已知AB是⊙O的弦,OB=4,∠OBC=30°,点C是弦AB上任意一点(不与A,B重合),连接CO并延长CO交⊙O于点D,连接AD、DB.当∠ADC=18°时,求∠DOB的度数.
20.已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.
21.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE CA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,过点A作AF⊥CD交CD的延长线于点F,若PB=OB,CD=,求圆O的半径.
22.如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=,tan∠ADC=3,求BE的长.
参考答案:
1.C
解:∵四边形是的内接四边形,
∴,
∵,
∴,
2.A
解:的半径是cm,点在圆内,
的长cm.
3.C
∵在中,,
∴,
4.D
解:∵四边形是的内接四边形,,
∴,
∴.
5.C
解:设运动的时间为t秒,
当点O到的距离为时,与相切,
∵开始时O点到的距离为,
∴当圆向右移动或时,点O到的距离为,此时与相切,
或,
即与直线在3秒或4秒时相切.
6.D
解:∵与的半径分别为和,且,
∴,即两圆圆心距离等于两圆半径之和.
∴和的位置关系是外切.
7.A
△ABC的外接圆的圆心在△ABC的内部,则△ABC是锐角三角形.
8.C
解:是的切线,为切点,
,
,
在中,,
.
9.C
∵OB=10cm,AB=20cm,
∴OA=OB+AB=30cm,
设扇形圆心角的度数为α,
∵纸面面积为π cm2,
∴,
∴α=150°,
10.C
解:A.利用圆周角不变,而∠ADC并不是圆周角,所以A是错误的;
B.若四边形ABCD是矩形,则∠ADC=90°,则D在大圆上,出现矛盾,所以B是错误的;
C.过D作DH⊥AC于H,BG⊥AC于G,
∴S四边形ABCD=S△ACD+S△ABC
=×AC×DH+×AC×BG
=×AC×(DH+BG)
≤×AC×BD.
∴四边形ABCD的最大面积等于AC BD.
∴C符合题意.
D.∵BD与AC不在同一条直线上.
∴AD的最大值不可能是×(AC+BD),故D错误.
11.72°/72度
解:∵∠ACB=∠AOB,∠ACB=36°,
∴∠AOB=2×∠ACB=72°.
故答案为:72°.
12.
解:由题意得:该扇形的面积为;
故答案为.
13.
根据圆锥的侧面积公式:,
故答案为:.
14.44;
∵四边形ABCD是⊙O的外切四边形,
∴AD+BC=AB+CD=10+12=22,
∴四边形ABCD的周长=22×2=44.
故答案为.
15.
解:设与正方形的边切于E,与切于F,
连接,,则四边形是正方形,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴的面积为,
故答案为:.
16./104度
解:
∵是的内切圆,
∴,,
∵,
∴,
∴;
17.30
解:∵是的内切圆,三个切点分别为,,,若,,
∴,,,
∵,
∴,
解得:,(不符合题意舍去),
∴,,
∴,
故答案为:;
18.
解:∵弦CD∥AB,
∴ ,
∴S阴影=S扇形COD==.
故答案为:.
19.96°
连接OA,由OA=OB,OA=OD,可得∠BAO=∠B,∠DAO=∠D,则可求得∠DAB的度数,又由圆周角等于同弧所对圆心角的一半,即可求得∠DOB的度数.
解;连接OA,
∵OA=OB=OD,
∴∠OAB=∠OBC=30°,∠OAD=∠ADC=18°,
∴∠DAB=∠DAO+∠BAO=48°,
由圆周角定理得:∠DOB=2∠DAB=96°.
20.(1)证明见解析;(2)
解:(1)连接OB、OD、OC,
∵ABCD是菱形,
∴CD=CB,
∵OC=OC,OD=OB,
∴△OCD≌△OCB,
∴∠ODC=∠OBC,
∵CD与⊙O相切,
∴OD⊥CD,
∴∠OBC=∠ODC=90°,
即OB⊥BC,点B在⊙O上,
∴BC与⊙O相切.
(2)∵ABCD是菱形,
∴∠A=∠DCB,
∵∠DOB与∠A所对的弧都是
∴∠DOB=2∠A,
由(1)知∠DOB+∠C=180°,
∴∠DOB=120°,∠DOC=60°,
∵OD=1,
∴OC=2,DC=
∴S阴影=2S△DOC-S扇形OBD=2××1×-=.
21.(1)证明见解析;
(2)⊙O的半径为4.
(1)证明:∵DC2=CE CA,
∴,
∵∠ACD=∠DCE,
∴△CAD△CDE,
∴∠CAD=∠CDE,
∵∠CAD=∠CBD,
∴∠CDB=∠CBD,
∴BC=DC;
(2)连接OC,如图,设⊙O的半径为r,
∵CD=CB,
∴,
∴∠BAC=∠CAD即∠BAD=2∠BAC,
∵∠BOC=2∠BAC,
∴∠BOC=∠BAD,
∴,
∴,
∵PB=OB=OA,
∴==2,
∵CD=,
∴PC=2CD=4,
∴PD=6,
∵∠PCB=∠CDB+∠CBD,∠CDB=∠CBD,∠BAD=2∠BAC,
∴∠PCB=∠PAD,
∵∠CPB=∠APD,
∴ ,
∴即,
∴r=4,即⊙O的半径为4.
22.(1)证明见解析;(2)
解:(1)证明:连结OA,OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB= 90°,
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BAE=45°,
∴∠OAE=∠OAB+∠BAE=90°,
∴OA⊥AE.
∵点A在⊙O上,
∴AE是⊙O的切线.
(2)解:过点A作AF⊥CD于点F,则∠AFC=∠AFD=90°.
∵AB=AD,
∴ =
∴∠ACD=∠ACB=45°,
在Rt△AFC中,
∵AC=,∠ACF=45°,
∴AF=CF=AC·sin∠ACF =3,
∵在Rt△AFD中, tan∠ADC=,
∴DF=1,
∴,
且CD= CF+DF=4,
∵四边形ABCD内接于⊙O,
∴∠ABE=∠CDA,
∵∠BAE=∠DCA,
∴△ABE∽△CDA,
∴,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆 易错知识点单选 强化练
2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.如图,点A,B,C,D在上,,则的度数为( )
A. B. C. D.
2.已知的半径是,点在圆内,则的长( )
A.小于 B.等于
C.大于 D.等于
3.如图,A,B,C是上的三个点,如果,那么的度数是( )
A. B. C. D.
4.如图,四边形是的内接四边形,若,则的度数为( )
A. B. C. D.
5.如图,在直线l上有相距的两点A和O(点A在点O的右侧),以O为圆心作半径为的圆,过点A作直线.将以的速度向右移动(点O始终在直线l上),则与直线在( )秒时相切
A.3 B.4 C.3或4 D.3或
6.已知与的半径分别为和,若.则与的位置关系是
A.外离 B.相交 C.内切 D.外切
7.△ABC的外心在三角形的内部,则△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
8.如图,是的切线,为切点,交于点,若,,则的长为( )
A.5 B.7 C.8 D.13
9.如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为π cm2,则扇形圆心角的度数为( )
A.120° B.140° C.150° D.160°
10.如图是两个同心圆,大圆的直径AC固定不动,小圆的直径BD绕着圆心0旋转,BD与AC不在同一条直线上,在BD旋转过程中,下面说法正确的是( )
A.∠ADC的大小始终不变 B.四边形ABCD存在是矩形的情形
C.四边形ABCD的最大面积等于AC·BD. D.AD的最大值等于(AC+BD)
二、填空题
11.如图,A、B、C点在圆O上, 若∠ACB=36°, 则∠AOB= .
12.扇形的半径为2,圆心角为90°,则该扇形的面积(结果保留)为 .
13.若圆锥的底面圆半径为2,母线长为5,则该圆锥的侧面积是 .(结果保留)
14.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=12,则四边形ABCD的周长为 .
15.如图,内切于正方形,为圆心,作,其两边分别交,于点,,若,则的面积为 .
16.如图,已知是的内切圆,点是内心,若,则等于 .
17.如图,在中,,是的内切圆,三个切点分别为,,,若,,则的面积是 .
18.如图,半圆O的直径AB=2,弦CD∥AB,∠COD=90°,则图中阴影部分的面积为 .
三、解答题
19.如图,已知AB是⊙O的弦,OB=4,∠OBC=30°,点C是弦AB上任意一点(不与A,B重合),连接CO并延长CO交⊙O于点D,连接AD、DB.当∠ADC=18°时,求∠DOB的度数.
20.已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.
21.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE CA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,过点A作AF⊥CD交CD的延长线于点F,若PB=OB,CD=,求圆O的半径.
22.如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=,tan∠ADC=3,求BE的长.
参考答案:
1.C
解:∵四边形是的内接四边形,
∴,
∵,
∴,
2.A
解:的半径是cm,点在圆内,
的长cm.
3.C
∵在中,,
∴,
4.D
解:∵四边形是的内接四边形,,
∴,
∴.
5.C
解:设运动的时间为t秒,
当点O到的距离为时,与相切,
∵开始时O点到的距离为,
∴当圆向右移动或时,点O到的距离为,此时与相切,
或,
即与直线在3秒或4秒时相切.
6.D
解:∵与的半径分别为和,且,
∴,即两圆圆心距离等于两圆半径之和.
∴和的位置关系是外切.
7.A
△ABC的外接圆的圆心在△ABC的内部,则△ABC是锐角三角形.
8.C
解:是的切线,为切点,
,
,
在中,,
.
9.C
∵OB=10cm,AB=20cm,
∴OA=OB+AB=30cm,
设扇形圆心角的度数为α,
∵纸面面积为π cm2,
∴,
∴α=150°,
10.C
解:A.利用圆周角不变,而∠ADC并不是圆周角,所以A是错误的;
B.若四边形ABCD是矩形,则∠ADC=90°,则D在大圆上,出现矛盾,所以B是错误的;
C.过D作DH⊥AC于H,BG⊥AC于G,
∴S四边形ABCD=S△ACD+S△ABC
=×AC×DH+×AC×BG
=×AC×(DH+BG)
≤×AC×BD.
∴四边形ABCD的最大面积等于AC BD.
∴C符合题意.
D.∵BD与AC不在同一条直线上.
∴AD的最大值不可能是×(AC+BD),故D错误.
11.72°/72度
解:∵∠ACB=∠AOB,∠ACB=36°,
∴∠AOB=2×∠ACB=72°.
故答案为:72°.
12.
解:由题意得:该扇形的面积为;
故答案为.
13.
根据圆锥的侧面积公式:,
故答案为:.
14.44;
∵四边形ABCD是⊙O的外切四边形,
∴AD+BC=AB+CD=10+12=22,
∴四边形ABCD的周长=22×2=44.
故答案为.
15.
解:设与正方形的边切于E,与切于F,
连接,,则四边形是正方形,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴的面积为,
故答案为:.
16./104度
解:
∵是的内切圆,
∴,,
∵,
∴,
∴;
17.30
解:∵是的内切圆,三个切点分别为,,,若,,
∴,,,
∵,
∴,
解得:,(不符合题意舍去),
∴,,
∴,
故答案为:;
18.
解:∵弦CD∥AB,
∴ ,
∴S阴影=S扇形COD==.
故答案为:.
19.96°
连接OA,由OA=OB,OA=OD,可得∠BAO=∠B,∠DAO=∠D,则可求得∠DAB的度数,又由圆周角等于同弧所对圆心角的一半,即可求得∠DOB的度数.
解;连接OA,
∵OA=OB=OD,
∴∠OAB=∠OBC=30°,∠OAD=∠ADC=18°,
∴∠DAB=∠DAO+∠BAO=48°,
由圆周角定理得:∠DOB=2∠DAB=96°.
20.(1)证明见解析;(2)
解:(1)连接OB、OD、OC,
∵ABCD是菱形,
∴CD=CB,
∵OC=OC,OD=OB,
∴△OCD≌△OCB,
∴∠ODC=∠OBC,
∵CD与⊙O相切,
∴OD⊥CD,
∴∠OBC=∠ODC=90°,
即OB⊥BC,点B在⊙O上,
∴BC与⊙O相切.
(2)∵ABCD是菱形,
∴∠A=∠DCB,
∵∠DOB与∠A所对的弧都是
∴∠DOB=2∠A,
由(1)知∠DOB+∠C=180°,
∴∠DOB=120°,∠DOC=60°,
∵OD=1,
∴OC=2,DC=
∴S阴影=2S△DOC-S扇形OBD=2××1×-=.
21.(1)证明见解析;
(2)⊙O的半径为4.
(1)证明:∵DC2=CE CA,
∴,
∵∠ACD=∠DCE,
∴△CAD△CDE,
∴∠CAD=∠CDE,
∵∠CAD=∠CBD,
∴∠CDB=∠CBD,
∴BC=DC;
(2)连接OC,如图,设⊙O的半径为r,
∵CD=CB,
∴,
∴∠BAC=∠CAD即∠BAD=2∠BAC,
∵∠BOC=2∠BAC,
∴∠BOC=∠BAD,
∴,
∴,
∵PB=OB=OA,
∴==2,
∵CD=,
∴PC=2CD=4,
∴PD=6,
∵∠PCB=∠CDB+∠CBD,∠CDB=∠CBD,∠BAD=2∠BAC,
∴∠PCB=∠PAD,
∵∠CPB=∠APD,
∴ ,
∴即,
∴r=4,即⊙O的半径为4.
22.(1)证明见解析;(2)
解:(1)证明:连结OA,OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB= 90°,
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BAE=45°,
∴∠OAE=∠OAB+∠BAE=90°,
∴OA⊥AE.
∵点A在⊙O上,
∴AE是⊙O的切线.
(2)解:过点A作AF⊥CD于点F,则∠AFC=∠AFD=90°.
∵AB=AD,
∴ =
∴∠ACD=∠ACB=45°,
在Rt△AFC中,
∵AC=,∠ACF=45°,
∴AF=CF=AC·sin∠ACF =3,
∵在Rt△AFD中, tan∠ADC=,
∴DF=1,
∴,
且CD= CF+DF=4,
∵四边形ABCD内接于⊙O,
∴∠ABE=∠CDA,
∵∠BAE=∠DCA,
∴△ABE∽△CDA,
∴,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
