选择必修第二册 第四章 4.3.1 等比数列的概念(第1课时)课件(共25张PPT)
文档属性
| 名称 | 选择必修第二册 第四章 4.3.1 等比数列的概念(第1课时)课件(共25张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 22:43:18 | ||
图片预览








文档简介
(共25张PPT)
选择必修2
第四章 数列
4.3 等比数列
4.3.1 等比数列的概念(第1课时)
教学目标
学习目标 数学素养
1.理解等比数列的定义,会判定数列是否是等比数列. 1.数学抽象素养和逻辑推理素养.
2.理解等比中项的概念并会运用. 2.数学抽象素养.
3.掌握等比数列的通项公式,并了解其推导过程,体会等比数列与指数函数的关系. 3.逻辑推理素养和数学运算素养.
温故知新
1.等差数列的概念
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列. 这个常数叫做等差数列的公差通常用字母d表示.
2.等差中项
等差数列的符号语言:an-an-1 = d (d是常数,n≥2,)
由三个数a,A,b组成的等差数列可以看成是最简单的等差数列.这时,A叫做a与b的等差中项.
2A=a+b或A=.
3.等差数列的通项公式
an=a1+(n-1)d.
首项为a1,公差为d的等差数列{an}的通项公式为
知新引入
我们知道,等差数列的特征是“从第2项起,每一项与它的前一项的差都等于同一个常数”,类比等差数列的研究思路和方法,从运算的角度出发,你觉得还有怎样的数列是值得研究的?
如果我们不是考虑相邻两项的差,而是考虑相邻两项的比,会得到什么样的数列呢?请看下面几个问题中的数列.
1.两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
9,92,93,…,910; ①
100,1002,1003,…,10010; ②
5,52,53,…,510. ③
古巴比伦用六十进制记数,这里转化为十进制.
2.《庄子·天下》中提到:“一尺之棰,日取其半,万世不竭.”如果把“一尺之棰”的长度看成单位“1”,那么从第1天开始,各天得到的“棰”的长度依次是:
④
知新探究
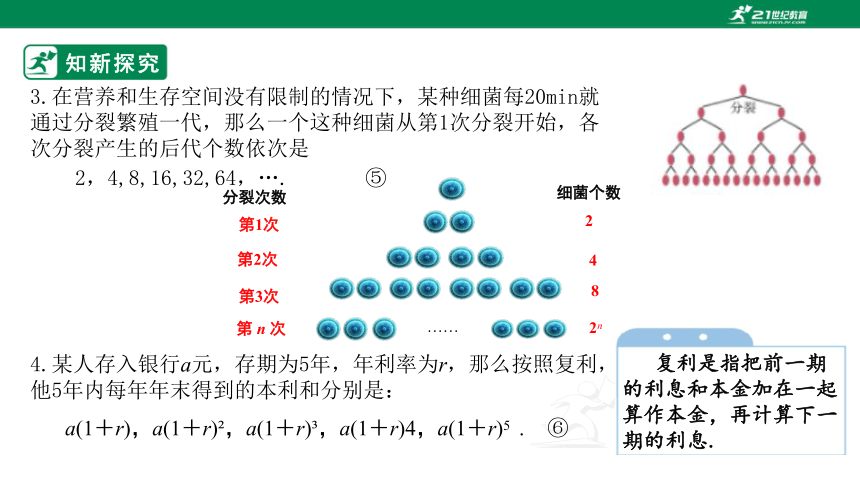
3.在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代,那么一个这种细菌从第1次分裂开始,各次分裂产生的后代个数依次是
2,4,8,16,32,64,…. ⑤
4.某人存入银行a元,存期为5年,年利率为r,那么按照复利,他5年内每年年末得到的本利和分别是:
细菌个数
第1次
第2次
第3次
2
4
第 n 次
……
分裂次数
8
2n
a(1+r),a(1+r) ,a(1+r) ,a(1+r)4,a(1+r)5 . ⑥
复利是指把前一期的利息和本金加在一起算作本金,再计算下一期的利息.
知新探究
9,92,93,…,910; ①
100,1002,1003,…,10010; ②
5,52,53,…,510. ③
④
我们可以通过除法运算探究以上数列的规律.
类比等差数列,你认为可以通过怎样的运算发现以下数列的取值规律?你发现了什么规律?
2,4,8,16,32,64,…. ⑤
a(1+r),a(1+r) ,a(1+r) ,a(1+r)4,a(1+r)5 . ⑥
如果用{an}表示数列①,那么有
数列①有这样的取值规律:从第2项起,每一项与它的前一项的比都等于 9.
.
其余数列也有这样的规律:从第2项起,每一项与前一项的比都等于同一个常数.
新知探究
类比等差数列的概念,从上述几个数列的规律中,你能否抽象出等比数列的概念吗?
等差数列
定义
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列(arithmetic progression). 这个常数叫做等差数列的公差(common difference),通常用字母d表示.
符号表示
an-an-1 = d (n≥2,)
()
等比数列
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列(geometric progression). 这个常数叫做等差数列的公比(common ratio),通常用字母q表示(显然q≠0).
(n≥2,).
().
知新探究
请大家说一说①,②,③,④,⑤,⑥这六个例子的公比分别是多少?
⑴公差q是由后项除以前项所得,不能用前项除以后项来求.
.
注意:
⑵符号表示:(n≥2,)或().
⑶等比数列的每一项和公比都不为0().
⑷当q=1时,{an}为非零常数数列;当q<0时,{an}是摆动数列(正负项交替).
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列(geometric progression). 这个常数叫做等差数列的公比(common ratio),通常用字母q表示(显然q≠0).
知新探究
由三个数a,A,b组成的等差数列,A叫做a与b的等差中项.此时,A=.
如果a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项(geometric mean).此时,G2=ab.
任意实数a与b有且只有一个等差中项.
在等差数列中,我们学习了等差中项的概念.通过类比,在等比数列中有什么相应的概念?如何定义?
⑴实数a与b有等比中项的条件是:a与b同号;
⑵若实数a与b有等比中项,则它们的等比中项为G=.
⑶一个等比数列从第2项起,每一项是它的前一项与后一项的等比中项.
新知探究
an+1=an q.
方法1:设一个等比数列的首项是a1,公比是q,根据等比数列的定义,可得
所以
a4=a3q=(a1q2)q=a1q3,
a2=a1q,
因此,首项为a1,公比为q的等比数列{an}的通项公式为
类比等差数列的通项公式,你能根据等比数列的定义推导它的通项公式吗?
a3=a2q=(a1q)q=a1q2,
……
由此可得
an=a1qn-1(n≥2).
又a1=a1q0=a1q1-1,这就是说,当n=1时上式也成立.
an=a1qn-1.
不完全归纳法
新知探究
q.
方法2:设一个等比数列的首项是a1,公比是q,根据等比数列的定义,可得
所以
q,
q,
因此,首项为a1,公比为q的等比数列{an}的通项公式为
类比等差数列的通项公式,你能根据等比数列的定义推导它的通项公式吗?
q,
…
这n-1个等式两边相乘,得
q(n≥2).
又a1=a1q0=a1q1-1,这就是说,当n=1时上式也成立.
an=a1qn-1.
累乘法
q(n≥2).
即an=a1qn-1(n≥2).
新知探究
类比于等差数列与一次函数,由an=可知,当q>0且q≠1时,等比数列的第n项an是指数函数当x=n时的函数值,即an=f(n).a1>0,q>0的情形如图所示.
.
反之,任给函数f(x)=kax(k,a为常数,k≠0,a>0,且a≠1),则f(1)=ka,f(2)=ka2,…,f(n)=kan,…构成一个等比数列{kan},其首项为ka,公比为a.
首项为a1,公比为q的等比数列{an}的通项公式为
an=a1qn-1.
指数型函数
新知探究
类比等差数列的性质,说说公比q>0的等比数列的单调性.
当q=1时,等比数列{an}是非零常数数列,不具备单调性.
新知探究
【例1】若等比数列{an}的第4项和第6项分别为48和12,求{an}的第5项.
分析:等比数列{an}由 a1,q确定,可利用条件列出a1,q的方程(组),进而求解.
解:
解法1:由a4=48,a6=12,得
.
②的两边分别除以①的两边,得
,
解得.
把代入①,得a1=384,
此时,24.
把代入①,得a1=-384,
此时,-24.
因此,{an}的第5项是24或-24.
新知探究
【例1】若等比数列{an}的第4项和第6项分别为48和12,求{an}的第5项.
解:
解法2:∵是a4和a6的等比中项,
∴.
∴.
因此,{an}的第5项是24或-24.
初试身手
方法1:∵a2+a5=18,a3+a6=9,
1.已知等比数列{an}中,a2+a5=18,a3+a6=9,an=1,求n.
即26-n=20.
解:
②的两边分别除以①的两边,得q=.
又an=1,
∴,
将q=代入①,得a1=32.
∴,
∴n=6.
初试身手
方法2:∵a3+a6=q(a2+a5),a2+a5=18,a3+a6=9,
1.已知等比数列{an}中,a2+a5=18,a3+a6=9,an=1,求n.
即26-n=20.
解:
又an=1,
∴q=,
将q=代入,得a1=32.
∴,
∴n=6.
知新探究
【例2】已知等比数列{an}的公比为q,试用{an}的第m项am表示an.
解:
由题意,得
,
∴.
①
②
②的两边分别除以①的两边,得
等比数列的任意一项都可以由该数列的某一项和公比表示.
我们由此可得等比数列的又一个通项公式.
.
知新探究
【例3】数列{an}共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132. 求这个数列.
解:
⑵设前三项的公比为q ,后三项的公差为d,则数列的各项依次为,80,80+d, 8+2d.
解方程组,得.
∴这个数列是20,40,80,96,112,或180,120,80,16,-48.
于是得,
分析:先利用已知条件表示出数列各项,再进一步根据条件列方程组求解.
初试身手
设这四个数依次为a-d,a,a+d,,则
2.有四个数,其中前三个数成等差数列,后三个是成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数.
故这四个数为0,4,8,16或15,9,3,1.
解:
当a=9,d=-6时,这四个数为15,9,3,1.
解得,
,
当a=4,d=4时,这四个数为0,4,8,16;
课堂小结
等差数列 等比数列
定义
符号表示
公差公比
通项公式
等差/等比中项
通项公式推导方法
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列
an-an-1 = d (n≥2,)
(n≥2,).
公差d可正、可负、可为零
公比q可正、可负但不可为零
an=a1+(n-1)d.
an=am+(n-m)d.
an=a1qn-1.
.
A是a与b的等差中项 A=.
G是a与b的等比中项 G2=ab(ab>0).
不完全归纳法
累加法
累乘法
作业布置
作业: P31 练习 第3,4,5题
P40 习题4.3 第1⑵,2题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修2
第四章 数列
4.3 等比数列
4.3.1 等比数列的概念(第1课时)
教学目标
学习目标 数学素养
1.理解等比数列的定义,会判定数列是否是等比数列. 1.数学抽象素养和逻辑推理素养.
2.理解等比中项的概念并会运用. 2.数学抽象素养.
3.掌握等比数列的通项公式,并了解其推导过程,体会等比数列与指数函数的关系. 3.逻辑推理素养和数学运算素养.
温故知新
1.等差数列的概念
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列. 这个常数叫做等差数列的公差通常用字母d表示.
2.等差中项
等差数列的符号语言:an-an-1 = d (d是常数,n≥2,)
由三个数a,A,b组成的等差数列可以看成是最简单的等差数列.这时,A叫做a与b的等差中项.
2A=a+b或A=.
3.等差数列的通项公式
an=a1+(n-1)d.
首项为a1,公差为d的等差数列{an}的通项公式为
知新引入
我们知道,等差数列的特征是“从第2项起,每一项与它的前一项的差都等于同一个常数”,类比等差数列的研究思路和方法,从运算的角度出发,你觉得还有怎样的数列是值得研究的?
如果我们不是考虑相邻两项的差,而是考虑相邻两项的比,会得到什么样的数列呢?请看下面几个问题中的数列.
1.两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
9,92,93,…,910; ①
100,1002,1003,…,10010; ②
5,52,53,…,510. ③
古巴比伦用六十进制记数,这里转化为十进制.
2.《庄子·天下》中提到:“一尺之棰,日取其半,万世不竭.”如果把“一尺之棰”的长度看成单位“1”,那么从第1天开始,各天得到的“棰”的长度依次是:
④
知新探究
3.在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代,那么一个这种细菌从第1次分裂开始,各次分裂产生的后代个数依次是
2,4,8,16,32,64,…. ⑤
4.某人存入银行a元,存期为5年,年利率为r,那么按照复利,他5年内每年年末得到的本利和分别是:
细菌个数
第1次
第2次
第3次
2
4
第 n 次
……
分裂次数
8
2n
a(1+r),a(1+r) ,a(1+r) ,a(1+r)4,a(1+r)5 . ⑥
复利是指把前一期的利息和本金加在一起算作本金,再计算下一期的利息.
知新探究
9,92,93,…,910; ①
100,1002,1003,…,10010; ②
5,52,53,…,510. ③
④
我们可以通过除法运算探究以上数列的规律.
类比等差数列,你认为可以通过怎样的运算发现以下数列的取值规律?你发现了什么规律?
2,4,8,16,32,64,…. ⑤
a(1+r),a(1+r) ,a(1+r) ,a(1+r)4,a(1+r)5 . ⑥
如果用{an}表示数列①,那么有
数列①有这样的取值规律:从第2项起,每一项与它的前一项的比都等于 9.
.
其余数列也有这样的规律:从第2项起,每一项与前一项的比都等于同一个常数.
新知探究
类比等差数列的概念,从上述几个数列的规律中,你能否抽象出等比数列的概念吗?
等差数列
定义
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列(arithmetic progression). 这个常数叫做等差数列的公差(common difference),通常用字母d表示.
符号表示
an-an-1 = d (n≥2,)
()
等比数列
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列(geometric progression). 这个常数叫做等差数列的公比(common ratio),通常用字母q表示(显然q≠0).
(n≥2,).
().
知新探究
请大家说一说①,②,③,④,⑤,⑥这六个例子的公比分别是多少?
⑴公差q是由后项除以前项所得,不能用前项除以后项来求.
.
注意:
⑵符号表示:(n≥2,)或().
⑶等比数列的每一项和公比都不为0().
⑷当q=1时,{an}为非零常数数列;当q<0时,{an}是摆动数列(正负项交替).
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列(geometric progression). 这个常数叫做等差数列的公比(common ratio),通常用字母q表示(显然q≠0).
知新探究
由三个数a,A,b组成的等差数列,A叫做a与b的等差中项.此时,A=.
如果a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项(geometric mean).此时,G2=ab.
任意实数a与b有且只有一个等差中项.
在等差数列中,我们学习了等差中项的概念.通过类比,在等比数列中有什么相应的概念?如何定义?
⑴实数a与b有等比中项的条件是:a与b同号;
⑵若实数a与b有等比中项,则它们的等比中项为G=.
⑶一个等比数列从第2项起,每一项是它的前一项与后一项的等比中项.
新知探究
an+1=an q.
方法1:设一个等比数列的首项是a1,公比是q,根据等比数列的定义,可得
所以
a4=a3q=(a1q2)q=a1q3,
a2=a1q,
因此,首项为a1,公比为q的等比数列{an}的通项公式为
类比等差数列的通项公式,你能根据等比数列的定义推导它的通项公式吗?
a3=a2q=(a1q)q=a1q2,
……
由此可得
an=a1qn-1(n≥2).
又a1=a1q0=a1q1-1,这就是说,当n=1时上式也成立.
an=a1qn-1.
不完全归纳法
新知探究
q.
方法2:设一个等比数列的首项是a1,公比是q,根据等比数列的定义,可得
所以
q,
q,
因此,首项为a1,公比为q的等比数列{an}的通项公式为
类比等差数列的通项公式,你能根据等比数列的定义推导它的通项公式吗?
q,
…
这n-1个等式两边相乘,得
q(n≥2).
又a1=a1q0=a1q1-1,这就是说,当n=1时上式也成立.
an=a1qn-1.
累乘法
q(n≥2).
即an=a1qn-1(n≥2).
新知探究
类比于等差数列与一次函数,由an=可知,当q>0且q≠1时,等比数列的第n项an是指数函数当x=n时的函数值,即an=f(n).a1>0,q>0的情形如图所示.
.
反之,任给函数f(x)=kax(k,a为常数,k≠0,a>0,且a≠1),则f(1)=ka,f(2)=ka2,…,f(n)=kan,…构成一个等比数列{kan},其首项为ka,公比为a.
首项为a1,公比为q的等比数列{an}的通项公式为
an=a1qn-1.
指数型函数
新知探究
类比等差数列的性质,说说公比q>0的等比数列的单调性.
当q=1时,等比数列{an}是非零常数数列,不具备单调性.
新知探究
【例1】若等比数列{an}的第4项和第6项分别为48和12,求{an}的第5项.
分析:等比数列{an}由 a1,q确定,可利用条件列出a1,q的方程(组),进而求解.
解:
解法1:由a4=48,a6=12,得
.
②的两边分别除以①的两边,得
,
解得.
把代入①,得a1=384,
此时,24.
把代入①,得a1=-384,
此时,-24.
因此,{an}的第5项是24或-24.
新知探究
【例1】若等比数列{an}的第4项和第6项分别为48和12,求{an}的第5项.
解:
解法2:∵是a4和a6的等比中项,
∴.
∴.
因此,{an}的第5项是24或-24.
初试身手
方法1:∵a2+a5=18,a3+a6=9,
1.已知等比数列{an}中,a2+a5=18,a3+a6=9,an=1,求n.
即26-n=20.
解:
②的两边分别除以①的两边,得q=.
又an=1,
∴,
将q=代入①,得a1=32.
∴,
∴n=6.
初试身手
方法2:∵a3+a6=q(a2+a5),a2+a5=18,a3+a6=9,
1.已知等比数列{an}中,a2+a5=18,a3+a6=9,an=1,求n.
即26-n=20.
解:
又an=1,
∴q=,
将q=代入,得a1=32.
∴,
∴n=6.
知新探究
【例2】已知等比数列{an}的公比为q,试用{an}的第m项am表示an.
解:
由题意,得
,
∴.
①
②
②的两边分别除以①的两边,得
等比数列的任意一项都可以由该数列的某一项和公比表示.
我们由此可得等比数列的又一个通项公式.
.
知新探究
【例3】数列{an}共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132. 求这个数列.
解:
⑵设前三项的公比为q ,后三项的公差为d,则数列的各项依次为,80,80+d, 8+2d.
解方程组,得.
∴这个数列是20,40,80,96,112,或180,120,80,16,-48.
于是得,
分析:先利用已知条件表示出数列各项,再进一步根据条件列方程组求解.
初试身手
设这四个数依次为a-d,a,a+d,,则
2.有四个数,其中前三个数成等差数列,后三个是成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数.
故这四个数为0,4,8,16或15,9,3,1.
解:
当a=9,d=-6时,这四个数为15,9,3,1.
解得,
,
当a=4,d=4时,这四个数为0,4,8,16;
课堂小结
等差数列 等比数列
定义
符号表示
公差公比
通项公式
等差/等比中项
通项公式推导方法
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列
an-an-1 = d (n≥2,)
(n≥2,).
公差d可正、可负、可为零
公比q可正、可负但不可为零
an=a1+(n-1)d.
an=am+(n-m)d.
an=a1qn-1.
.
A是a与b的等差中项 A=.
G是a与b的等比中项 G2=ab(ab>0).
不完全归纳法
累加法
累乘法
作业布置
作业: P31 练习 第3,4,5题
P40 习题4.3 第1⑵,2题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
