2024-2025学年北师大版八年级数学上册 3.2.2平面直角坐标系 课件(共21张PPT)
文档属性
| 名称 | 2024-2025学年北师大版八年级数学上册 3.2.2平面直角坐标系 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 482.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
3.2.2平面直角坐标系
2024-2025学年北师大版八年级数学上册★★
教学目标
1、知道与坐标轴平行的直线上点的坐标的特征
2、掌握直角坐标系点的对称特征
3、通过由点确定坐标到根据坐标描点的转化过程,进一步培养学生的能力。
情景导入
-2
-1
0
1
2
实数与数轴上的点有怎样的关系?
实数和数轴上的点一一对应:
每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.
新知讲解
(-4,-2)
A
B
(3,4)
M
N
E
F
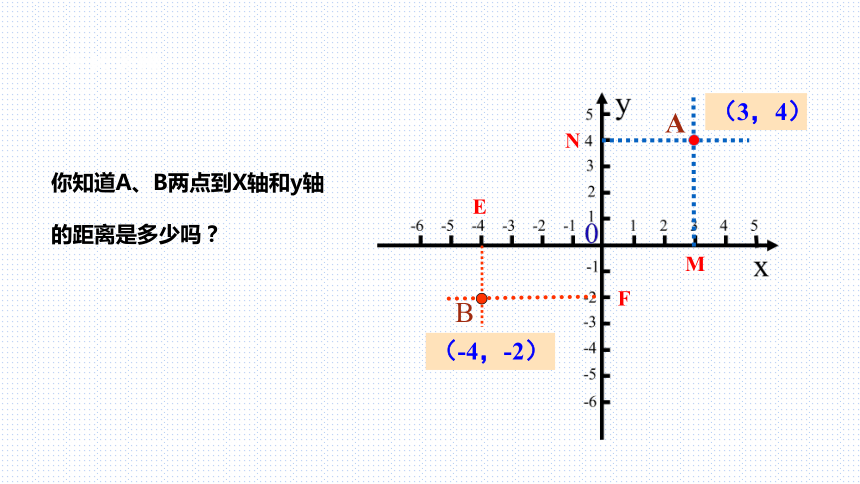
你知道A、B两点到X轴和y轴的距离是多少吗?
探究新知
点到坐标轴的距离
点A(a,b)到x轴的距离为,到y轴的距离为
点A(2,3)到x轴的距离是 ,到y轴的距离是 .
点B(-5,4)到x轴的距离是 ,到y轴的距离是 .
点C(-2,-3)到x轴的距离是 ,到y轴的距离是 .
点D(2,3)到x轴的距离是 ,到y轴的距离是 .
3
2
4
5
3
2
3
2
典例精析
例2、在直角坐标系中描出下列各点,并将各组内这些点依次用线段连接.
(1)D(-3,5), E(-7, 3), C(1,3), D(-3,5);
(2)F(-6,3), G(-6,0),A(0,0), B(0,3);
观察所描出的图形,它像什么?根据图形回答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段EC与x轴有什么位置关系?点E和点C的坐标有什
么特点?线段EC上其他点的坐标呢?
(3)点F和点G的横坐标有什么共同特点?线段FG与y轴有
怎样的位置关系?
典例精析
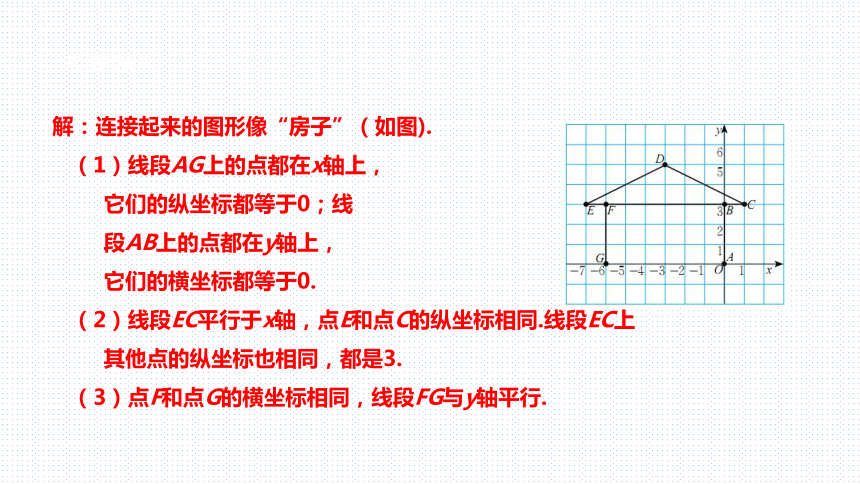
解:连接起来的图形像“房子”(如图).
(1)线段AG上的点都在x轴上,
它们的纵坐标都等于0;线
段AB上的点都在y轴上,
它们的横坐标都等于0.
(2)线段EC平行于x轴,点E和点C的纵坐标相同.线段EC上
其他点的纵坐标也相同,都是3.
(3)点F和点G的横坐标相同,线段FG与y轴平行.
归纳总结
“平行于两轴的直线上的点”的坐标特征:
平行于x轴直线上的点纵坐标相同
平行于y轴直线上的点横坐标相同
纵坐标相同的点的连线平行于x轴
横坐标相同的点的连线平行于y轴
反过来也成立
议一议
在平面直角坐标系中,坐标轴上的点的坐标有什么特点?
在x轴上的点,纵坐标等于0.
在y轴上的点,横坐标等于0.
做一做
如图是一个笑脸.
(1)在“笑脸”上找出几个位于第一象
限的点,指出它们的坐标,说说这些
点的坐标有什么特点.
(2)在其他象限内分别找几个点,看看
其他各个象限内的点的坐标有什么特点.
(3)不描出点,分别判断A(1, 2),B(-1, -3), C(2, -1), D(-3, 4)所在
的象限.
归纳总结
1.各象限内点的特点
点M(x,y)所处的位置 坐标特征
象限内的点 点M在第一象限
点M在第二象限
点M在第三象限
点M在第四象限
M(正,正)
M(负,正)
M(负,负)
M(正,负)
归纳总结
2.各象限的角平分线上的点的坐标特点:
横,纵坐标
第一三象限角平分线上
第二四象限角平分线上
y = x 或y-x=0
y = - x或y+x=0
归纳总结
⑴ x轴上的点,纵坐标为0。 y轴上的点,横坐标为0。
⑵ 第一、三象限夹角平分线上的点,纵横坐标相等。
第二、四象限夹角平分线上的点,纵横坐标互为相反数。
⑶与x轴平行(或与y轴垂直)的直线上的点纵坐标都相同。
与y轴平行(或与x轴垂直)的直线上的点横坐标都相同。
3.特殊位置的点的坐标特点:
归纳总结
⑷关于x轴对称的点横坐标相同、纵坐标互为相反数。
关于y轴对称的点纵坐标相同、横坐标互为相反数。
关于原点对称的点纵横坐标都互为相反数。
⑸平面直角坐标系中有一点P(a , b),点P到x轴的距离是这个点的纵坐标的绝对值;点P到y轴的距离是这个点的横坐标的绝对值.
课堂练习
1.下列各点中,在第二象限的点是( )
A.( 2,3) B.(2,-1) C.(-2,-6) D.(-1,2 )
2.已知点A(m ,2)在y轴上,则m+1等于( )
A.-1 B.1 C.0 D.±1
3.已知点A(a ,b)在第四象限,则点B(b,a)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
B
D
课堂练习
4.已知点P(x+6,x-4)在y轴上,则点P 的坐标是__________.
(0,-10)
5.若 mn=0,则点 P(m,n)必定在 上.
6.已知点 P(a,b),Q(3,6),且 PQ∥x轴,则b的值为 .
坐标轴
6
课堂练习
7.已知点P(3m-6,m+1),试分别根据下列条件,求出点P的坐标:
(1)点P在y轴上;(2)点P在x轴上;
(3)点P的纵坐标比横坐标大5;
(4)点P在过点A(-1,2)且与x轴平行的直线上.
解:(1)因为点P(3m-6,m+1)在y轴上,
所以3m-6=0,解得m=2.
所以m+1=2+1=3.
所以点P的坐标为(0,3).
课堂练习
(2)因为点P(3m-6,m+1)在x轴上,所以m+1=0,
解得m=-1.
所以3m-6=3×(-1)-6=-9.
所以点P的坐标为(-9,0).
(3)因为点P(3m-6,m+1)的纵坐标比横坐标大5,
所以m+1-(3m-6)=5,解得m=1.
所以3m-6=3×1-6=-3,m+1=1+1=2.
所以点P的坐标为(-3,2).
课堂练习
(4)因为点P(3m-6,m+1)在过点A(-1,2)且与x轴平行的直线上,
所以m+1=2,解得m=1.
所以3m-6=3×1-6=-3.
所以点P的坐标为(-3,2).
课堂总结
1.平行于x轴的直线上的点的纵坐标相等;平行于y轴的直线上的点的横坐标相等.
2.关于x轴对称的点,横坐标相等,纵坐标互为相反数;关于y轴对称的点,横坐标互为相反数,纵坐标相等.
3.第一、三象限内坐标轴夹角平分线上的点,横坐标与纵坐标相等;第二、四象限内坐标轴夹角平分线上的点,横坐标与纵坐标互为相反数.
板书设计
平面直角坐标系
1.坐标轴上的点坐标
2.平行于坐标轴的直线上的点
3.象限角平分线上的点
3.2.2平面直角坐标系
2024-2025学年北师大版八年级数学上册★★
教学目标
1、知道与坐标轴平行的直线上点的坐标的特征
2、掌握直角坐标系点的对称特征
3、通过由点确定坐标到根据坐标描点的转化过程,进一步培养学生的能力。
情景导入
-2
-1
0
1
2
实数与数轴上的点有怎样的关系?
实数和数轴上的点一一对应:
每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.
新知讲解
(-4,-2)
A
B
(3,4)
M
N
E
F
你知道A、B两点到X轴和y轴的距离是多少吗?
探究新知
点到坐标轴的距离
点A(a,b)到x轴的距离为,到y轴的距离为
点A(2,3)到x轴的距离是 ,到y轴的距离是 .
点B(-5,4)到x轴的距离是 ,到y轴的距离是 .
点C(-2,-3)到x轴的距离是 ,到y轴的距离是 .
点D(2,3)到x轴的距离是 ,到y轴的距离是 .
3
2
4
5
3
2
3
2
典例精析
例2、在直角坐标系中描出下列各点,并将各组内这些点依次用线段连接.
(1)D(-3,5), E(-7, 3), C(1,3), D(-3,5);
(2)F(-6,3), G(-6,0),A(0,0), B(0,3);
观察所描出的图形,它像什么?根据图形回答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段EC与x轴有什么位置关系?点E和点C的坐标有什
么特点?线段EC上其他点的坐标呢?
(3)点F和点G的横坐标有什么共同特点?线段FG与y轴有
怎样的位置关系?
典例精析
解:连接起来的图形像“房子”(如图).
(1)线段AG上的点都在x轴上,
它们的纵坐标都等于0;线
段AB上的点都在y轴上,
它们的横坐标都等于0.
(2)线段EC平行于x轴,点E和点C的纵坐标相同.线段EC上
其他点的纵坐标也相同,都是3.
(3)点F和点G的横坐标相同,线段FG与y轴平行.
归纳总结
“平行于两轴的直线上的点”的坐标特征:
平行于x轴直线上的点纵坐标相同
平行于y轴直线上的点横坐标相同
纵坐标相同的点的连线平行于x轴
横坐标相同的点的连线平行于y轴
反过来也成立
议一议
在平面直角坐标系中,坐标轴上的点的坐标有什么特点?
在x轴上的点,纵坐标等于0.
在y轴上的点,横坐标等于0.
做一做
如图是一个笑脸.
(1)在“笑脸”上找出几个位于第一象
限的点,指出它们的坐标,说说这些
点的坐标有什么特点.
(2)在其他象限内分别找几个点,看看
其他各个象限内的点的坐标有什么特点.
(3)不描出点,分别判断A(1, 2),B(-1, -3), C(2, -1), D(-3, 4)所在
的象限.
归纳总结
1.各象限内点的特点
点M(x,y)所处的位置 坐标特征
象限内的点 点M在第一象限
点M在第二象限
点M在第三象限
点M在第四象限
M(正,正)
M(负,正)
M(负,负)
M(正,负)
归纳总结
2.各象限的角平分线上的点的坐标特点:
横,纵坐标
第一三象限角平分线上
第二四象限角平分线上
y = x 或y-x=0
y = - x或y+x=0
归纳总结
⑴ x轴上的点,纵坐标为0。 y轴上的点,横坐标为0。
⑵ 第一、三象限夹角平分线上的点,纵横坐标相等。
第二、四象限夹角平分线上的点,纵横坐标互为相反数。
⑶与x轴平行(或与y轴垂直)的直线上的点纵坐标都相同。
与y轴平行(或与x轴垂直)的直线上的点横坐标都相同。
3.特殊位置的点的坐标特点:
归纳总结
⑷关于x轴对称的点横坐标相同、纵坐标互为相反数。
关于y轴对称的点纵坐标相同、横坐标互为相反数。
关于原点对称的点纵横坐标都互为相反数。
⑸平面直角坐标系中有一点P(a , b),点P到x轴的距离是这个点的纵坐标的绝对值;点P到y轴的距离是这个点的横坐标的绝对值.
课堂练习
1.下列各点中,在第二象限的点是( )
A.( 2,3) B.(2,-1) C.(-2,-6) D.(-1,2 )
2.已知点A(m ,2)在y轴上,则m+1等于( )
A.-1 B.1 C.0 D.±1
3.已知点A(a ,b)在第四象限,则点B(b,a)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
B
D
课堂练习
4.已知点P(x+6,x-4)在y轴上,则点P 的坐标是__________.
(0,-10)
5.若 mn=0,则点 P(m,n)必定在 上.
6.已知点 P(a,b),Q(3,6),且 PQ∥x轴,则b的值为 .
坐标轴
6
课堂练习
7.已知点P(3m-6,m+1),试分别根据下列条件,求出点P的坐标:
(1)点P在y轴上;(2)点P在x轴上;
(3)点P的纵坐标比横坐标大5;
(4)点P在过点A(-1,2)且与x轴平行的直线上.
解:(1)因为点P(3m-6,m+1)在y轴上,
所以3m-6=0,解得m=2.
所以m+1=2+1=3.
所以点P的坐标为(0,3).
课堂练习
(2)因为点P(3m-6,m+1)在x轴上,所以m+1=0,
解得m=-1.
所以3m-6=3×(-1)-6=-9.
所以点P的坐标为(-9,0).
(3)因为点P(3m-6,m+1)的纵坐标比横坐标大5,
所以m+1-(3m-6)=5,解得m=1.
所以3m-6=3×1-6=-3,m+1=1+1=2.
所以点P的坐标为(-3,2).
课堂练习
(4)因为点P(3m-6,m+1)在过点A(-1,2)且与x轴平行的直线上,
所以m+1=2,解得m=1.
所以3m-6=3×1-6=-3.
所以点P的坐标为(-3,2).
课堂总结
1.平行于x轴的直线上的点的纵坐标相等;平行于y轴的直线上的点的横坐标相等.
2.关于x轴对称的点,横坐标相等,纵坐标互为相反数;关于y轴对称的点,横坐标互为相反数,纵坐标相等.
3.第一、三象限内坐标轴夹角平分线上的点,横坐标与纵坐标相等;第二、四象限内坐标轴夹角平分线上的点,横坐标与纵坐标互为相反数.
板书设计
平面直角坐标系
1.坐标轴上的点坐标
2.平行于坐标轴的直线上的点
3.象限角平分线上的点
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
