25.3. 用频率估计概率课件
文档属性
| 名称 | 25.3. 用频率估计概率课件 |  | |
| 格式 | rar | ||
| 文件大小 | 876.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-31 22:20:00 | ||
图片预览








文档简介
课件26张PPT。25.3 用频率估计概率南门学校 九年(1)(2)班普查: 为了一定的目的,而对考察对象进行全面的调查,称为普查;频数:在考察中,每个对象出现的次数称为频数,
频率 而每个对象出现的次数与总次数的比值称为频率.总体: 所要考察对象的全体,称为总体,
个体 而组成总体的每一个考察对象称为个体;抽样调查:从总体中抽取部分个体进行调查,这种调查称为抽样调查;
样本:从总体中抽取的一部分个体叫做总体的一个样本;概率:事件发生的可能性,也称为事件发生的概率.必然事件发生的概率为1(或100%),记作P(必然事件)=1;
不可能事件发生的概率为0,记作P(不可能事件)=0;
随机事件(不确定事件)发生的概率介于0~1之间,即0如果A为随机事件(不确定事件),那么0色,另一面涂有黄色;硬币2的一面涂
有黄色,另一面涂有蓝色;硬币3的一
面涂有蓝色,另一面涂有红色。现将
这三枚硬币随意抛出,求两枚的颜色
相同的概率。用什么方法求概率?归纳1、列举的方法:(1)直接列举法:事件结果显而易见,可能性较少;(2)“列表”法:事件结果较复杂,可能性较多;(3)“树形图”法:事件结果较复杂,步骤较多。复习1、有三枚硬币,硬币1的一面涂有红
色,另一面涂有黄色;硬币2的一面涂
有黄色,另一面涂有蓝色;硬币3的一
面涂有蓝色,另一面涂有红色。现将
这三枚硬币随意抛出,求两枚的颜色
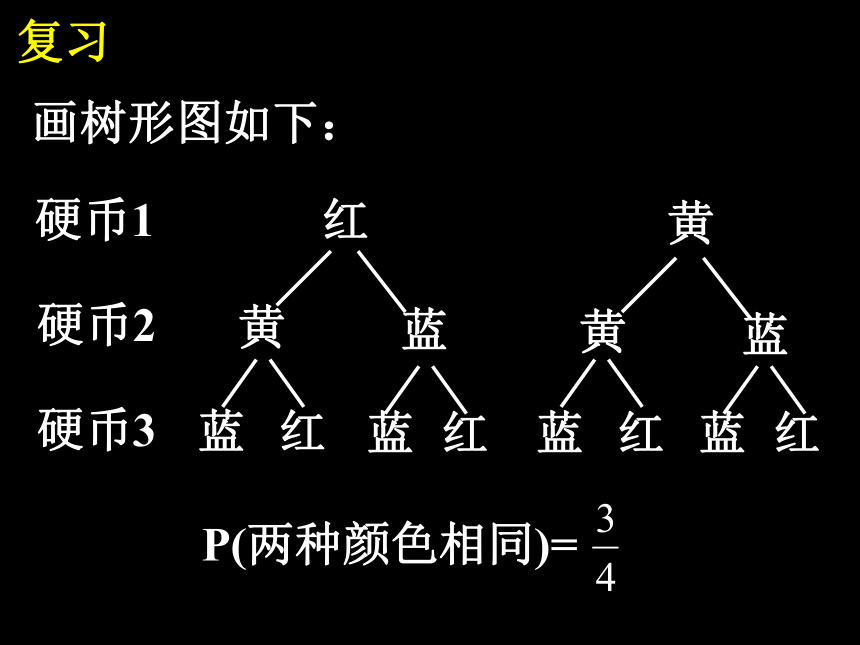
相同的概率。复习画树形图如下:硬币1硬币2硬币3红黄黄蓝黄蓝蓝红蓝红蓝红蓝红P(两种颜色相同)=复习2、等可能事件概率公式:(1)所有可能结果是有限个;3、求等可能事件概率的条件:(2)每种结果的可能性都相等。导入※、如图,有一枚质地均匀的硬币,将
它抛出后,你知道正面朝上的概率吗?正(1)是不是等可能事件?(2)用什么方法求概率?反所有可能结果是有限个;每种结果的可能性都相等。用列举法求概率。导入※、如图,有一枚图钉,将它抛出后,
要考察钉尖的朝向上的概率。(1)钉尖的朝向有几种可能的结果?钉尖朝上钉尖朝上(2)这两种结果可能性相等吗?这两种结果可能性不相等。用列举法求概率的条件是什么?(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.当实验的所有结果不是有限个;或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢?答:在同样条件下,通过大量反复的试验,根据一个随机事件发生的频率所逐渐稳定到的常数,可以估计这个事件发生的概率。 当试验的可能结果有很多并且各种结果发生的可能性相等时,我们可以用 的方式得出概率,当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,我们一般还要通过统计频率来估计概率. P (A) = 在同样条件下,大量重复试验时,根据一个随机事件发生的频率所逐 渐稳定到的常数,可以估计这个事件发生的概率.由频率可以估计概率
是由瑞士数学家雅各
布·伯努利(1654-
1705)最早阐明的,
因而他被公认为是概
率论的先驱之一.一 . 利用频率估计概率 问题1 某林业部门要考查某种幼树在一定条件的移植的成活率,应采用什么具体做法?
下表是一张模拟的统计表,请补出表中的空缺,并完成表后的填空.二. 思考解答0.940.9230.8830.9050.897从表可以发现,幼树移植成活的频率在_________左右摆动,并
且随着统计数据的增加,这种规律愈加越明显,所以估计幼树
移植成活率的概率为________0.990%问题2 某水果公司以2元/千克的成本新进了10 000千克的柑橘,如果公司希望这些柑橘能够获得利润5 000元,那么在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”统计,并把获得的数据记录在表中,请你帮忙完成此表.0.1010.0970.0970.1030.1010.0980.0990.103 从表可以看出,柑橘损坏的频率在常数_____左右摆动,并且随统计量的增加这种规律逐渐______,那么可以把柑橘损坏的概率估计为这个常数.如果估计这个概率为0.1,则柑橘完好的概率为_______.思 考0.1稳定0.9设每千克柑橘的销价为x元,则应有(x-2.22)×9 000=5 000解得 x≈2.8因此,出售柑橘时每千克大约定价为2.8元可获利润5 000元. 根据估计的概率可以知道,在10 000千克柑橘中完好柑橘的质量为
10 000×0.9=9 000千克,完好柑橘的实际成本为为简单起见,我们能否直接把表中500千克柑橘对应的柑橘损坏的频率看作柑橘损坏的频率看作柑橘损坏的概率?应该可以的因为500千克柑橘损坏51.54千克,损坏率是0.103,可以近似的估算是柑橘的损坏概率
某农科所在相同条件下做了某作物种子发芽率的实验,结果如下表所示:一般地,1 000千克种子中大约有多少是不能发芽的?练 习0.940.940.940.960.870.890.890.90.90.98一般地,1 000千克种子中大约有多少是不能发芽的?解答:这批种子的发芽的频率稳定在0.9即种子发芽的概率为90%,不发芽的概率为0.1,机不发芽率为10%所以: 1000×10%=100千克1000千克种子大约有100千克是不能发芽的.上面两个问题,都不属于结果可能性相等的类型.移植中有两种情况活或死.它们的可能性并不相等, 事件发生的概率并不都为50%.柑橘是好的还是坏的两种事件发生的概率也不相等.因此也不能简单的用50%来表示它发生的概率.应该如何做呢?翻到课本157页.在相同情况下随机的抽取若干个体进行实验,
进行实验统计.并计算事件发生的频率
根据频率估计该事件发生的概率.当试验次数很大时,一个事件发生频率也稳定在相应的概率附近.因此,我们可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.1.某种油菜籽在相同条件下的发芽试验结果表: 当试验的油菜籽的粒数很多时,油菜籽发芽
的频率 接近于常数0.9,于是我们说它的概率是0.9。2. 对某电视机厂生产的电视机进行抽样检测的数据如下: (1)计算表中优等品的各个频率;
(2)该厂生产的电视机优等品的概率是多少? 5.如图,小明、小华用4张扑克牌(方块2、黑桃4、黑桃5、梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的牌不放回。
(1)若小明恰好抽到了黑桃4。
①请在下边框中绘制这种情况的树状图;②求小华抽出的牌面数字比4大的概率。
(2)小明、小华约定:若小明抽到的牌面数字比小华的大,则小明胜;反之,则小明负。你认为这个游戏是否公平?说明你的理由。 结 束 寄 语不经历风雨,怎能见彩虹!再 见
频率 而每个对象出现的次数与总次数的比值称为频率.总体: 所要考察对象的全体,称为总体,
个体 而组成总体的每一个考察对象称为个体;抽样调查:从总体中抽取部分个体进行调查,这种调查称为抽样调查;
样本:从总体中抽取的一部分个体叫做总体的一个样本;概率:事件发生的可能性,也称为事件发生的概率.必然事件发生的概率为1(或100%),记作P(必然事件)=1;
不可能事件发生的概率为0,记作P(不可能事件)=0;
随机事件(不确定事件)发生的概率介于0~1之间,即0
有黄色,另一面涂有蓝色;硬币3的一
面涂有蓝色,另一面涂有红色。现将
这三枚硬币随意抛出,求两枚的颜色
相同的概率。用什么方法求概率?归纳1、列举的方法:(1)直接列举法:事件结果显而易见,可能性较少;(2)“列表”法:事件结果较复杂,可能性较多;(3)“树形图”法:事件结果较复杂,步骤较多。复习1、有三枚硬币,硬币1的一面涂有红
色,另一面涂有黄色;硬币2的一面涂
有黄色,另一面涂有蓝色;硬币3的一
面涂有蓝色,另一面涂有红色。现将
这三枚硬币随意抛出,求两枚的颜色
相同的概率。复习画树形图如下:硬币1硬币2硬币3红黄黄蓝黄蓝蓝红蓝红蓝红蓝红P(两种颜色相同)=复习2、等可能事件概率公式:(1)所有可能结果是有限个;3、求等可能事件概率的条件:(2)每种结果的可能性都相等。导入※、如图,有一枚质地均匀的硬币,将
它抛出后,你知道正面朝上的概率吗?正(1)是不是等可能事件?(2)用什么方法求概率?反所有可能结果是有限个;每种结果的可能性都相等。用列举法求概率。导入※、如图,有一枚图钉,将它抛出后,
要考察钉尖的朝向上的概率。(1)钉尖的朝向有几种可能的结果?钉尖朝上钉尖朝上(2)这两种结果可能性相等吗?这两种结果可能性不相等。用列举法求概率的条件是什么?(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.当实验的所有结果不是有限个;或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢?答:在同样条件下,通过大量反复的试验,根据一个随机事件发生的频率所逐渐稳定到的常数,可以估计这个事件发生的概率。 当试验的可能结果有很多并且各种结果发生的可能性相等时,我们可以用 的方式得出概率,当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,我们一般还要通过统计频率来估计概率. P (A) = 在同样条件下,大量重复试验时,根据一个随机事件发生的频率所逐 渐稳定到的常数,可以估计这个事件发生的概率.由频率可以估计概率
是由瑞士数学家雅各
布·伯努利(1654-
1705)最早阐明的,
因而他被公认为是概
率论的先驱之一.一 . 利用频率估计概率 问题1 某林业部门要考查某种幼树在一定条件的移植的成活率,应采用什么具体做法?
下表是一张模拟的统计表,请补出表中的空缺,并完成表后的填空.二. 思考解答0.940.9230.8830.9050.897从表可以发现,幼树移植成活的频率在_________左右摆动,并
且随着统计数据的增加,这种规律愈加越明显,所以估计幼树
移植成活率的概率为________0.990%问题2 某水果公司以2元/千克的成本新进了10 000千克的柑橘,如果公司希望这些柑橘能够获得利润5 000元,那么在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”统计,并把获得的数据记录在表中,请你帮忙完成此表.0.1010.0970.0970.1030.1010.0980.0990.103 从表可以看出,柑橘损坏的频率在常数_____左右摆动,并且随统计量的增加这种规律逐渐______,那么可以把柑橘损坏的概率估计为这个常数.如果估计这个概率为0.1,则柑橘完好的概率为_______.思 考0.1稳定0.9设每千克柑橘的销价为x元,则应有(x-2.22)×9 000=5 000解得 x≈2.8因此,出售柑橘时每千克大约定价为2.8元可获利润5 000元. 根据估计的概率可以知道,在10 000千克柑橘中完好柑橘的质量为
10 000×0.9=9 000千克,完好柑橘的实际成本为为简单起见,我们能否直接把表中500千克柑橘对应的柑橘损坏的频率看作柑橘损坏的频率看作柑橘损坏的概率?应该可以的因为500千克柑橘损坏51.54千克,损坏率是0.103,可以近似的估算是柑橘的损坏概率
某农科所在相同条件下做了某作物种子发芽率的实验,结果如下表所示:一般地,1 000千克种子中大约有多少是不能发芽的?练 习0.940.940.940.960.870.890.890.90.90.98一般地,1 000千克种子中大约有多少是不能发芽的?解答:这批种子的发芽的频率稳定在0.9即种子发芽的概率为90%,不发芽的概率为0.1,机不发芽率为10%所以: 1000×10%=100千克1000千克种子大约有100千克是不能发芽的.上面两个问题,都不属于结果可能性相等的类型.移植中有两种情况活或死.它们的可能性并不相等, 事件发生的概率并不都为50%.柑橘是好的还是坏的两种事件发生的概率也不相等.因此也不能简单的用50%来表示它发生的概率.应该如何做呢?翻到课本157页.在相同情况下随机的抽取若干个体进行实验,
进行实验统计.并计算事件发生的频率
根据频率估计该事件发生的概率.当试验次数很大时,一个事件发生频率也稳定在相应的概率附近.因此,我们可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.1.某种油菜籽在相同条件下的发芽试验结果表: 当试验的油菜籽的粒数很多时,油菜籽发芽
的频率 接近于常数0.9,于是我们说它的概率是0.9。2. 对某电视机厂生产的电视机进行抽样检测的数据如下: (1)计算表中优等品的各个频率;
(2)该厂生产的电视机优等品的概率是多少? 5.如图,小明、小华用4张扑克牌(方块2、黑桃4、黑桃5、梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的牌不放回。
(1)若小明恰好抽到了黑桃4。
①请在下边框中绘制这种情况的树状图;②求小华抽出的牌面数字比4大的概率。
(2)小明、小华约定:若小明抽到的牌面数字比小华的大,则小明胜;反之,则小明负。你认为这个游戏是否公平?说明你的理由。 结 束 寄 语不经历风雨,怎能见彩虹!再 见
同课章节目录
