直线与圆的位置关系第三课时
文档属性
| 名称 | 直线与圆的位置关系第三课时 |

|
|
| 格式 | rar | ||
| 文件大小 | 106.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-31 00:00:00 | ||
图片预览


文档简介
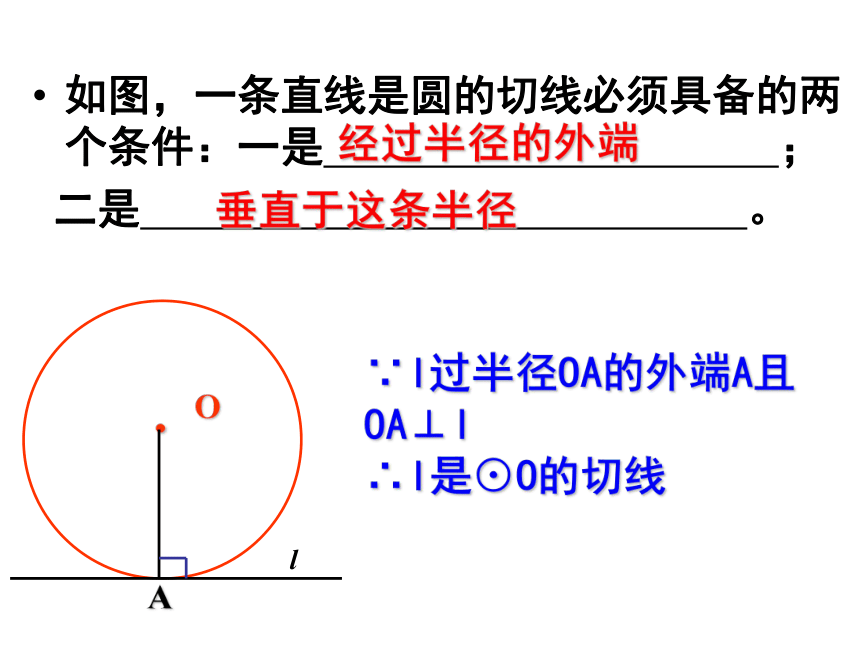
课件16张PPT。直线与圆的位置关系(三)保康县实验中学 九年级数学组如图,一条直线是圆的切线必须具备的两个条件:一是 ;
二是 。 经过半径的外端垂直于这条半径∵l过半径OA的外端A且OA⊥l
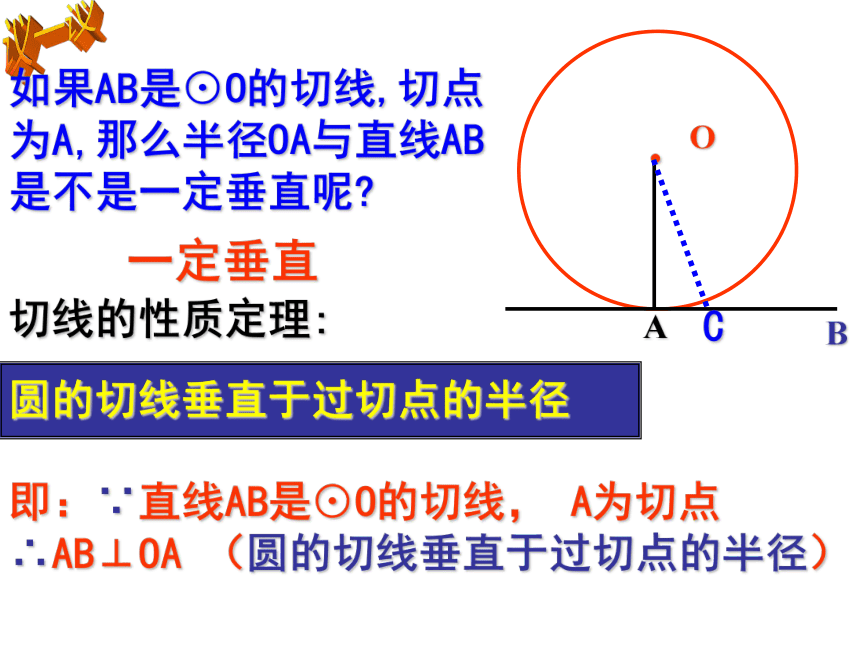
∴l是⊙O的切线议一议如果AB是⊙O的切线,切点为A,那么半径OA与直线AB是不是一定垂直呢?一定垂直切线的性质定理:圆的切线垂直于过切点的半径即:∵直线AB是⊙O的切线, A为切点
∴AB⊥OA (圆的切线垂直于过切点的半径)切线的性质切线与圆有 公共点;
圆心到直线的距离等于 。
切线垂直于 的半径。
经过圆心且垂直于切线的直线必过 。
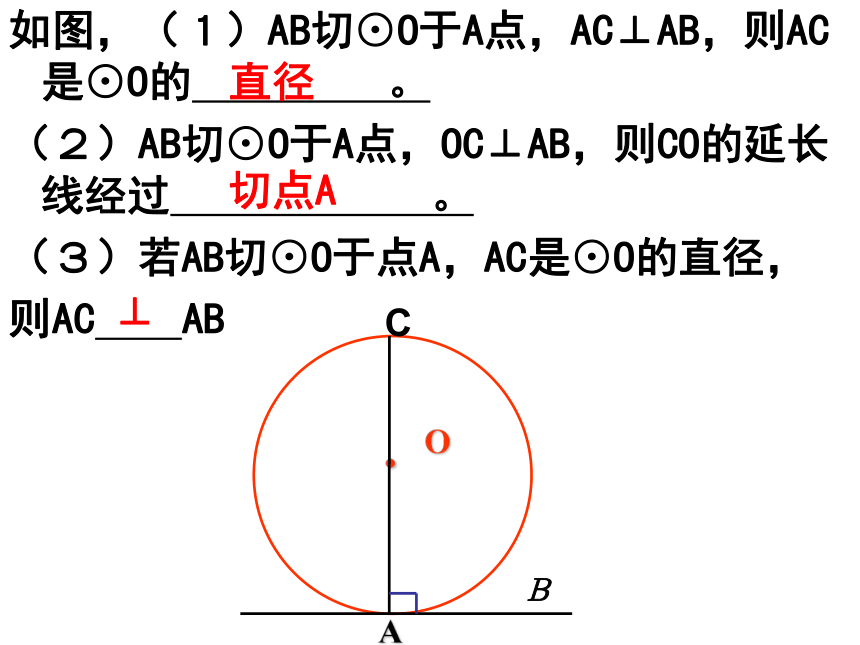
过切点且垂直于切线的直线必过 。唯一圆的半径过切点切点圆心如图,(1)AB切⊙O于A点,AC⊥AB,则AC是⊙O的 。
(2)AB切⊙O于A点,OC⊥AB,则CO的延长线经过 。
(3)若AB切⊙O于点A,AC是⊙O的直径,
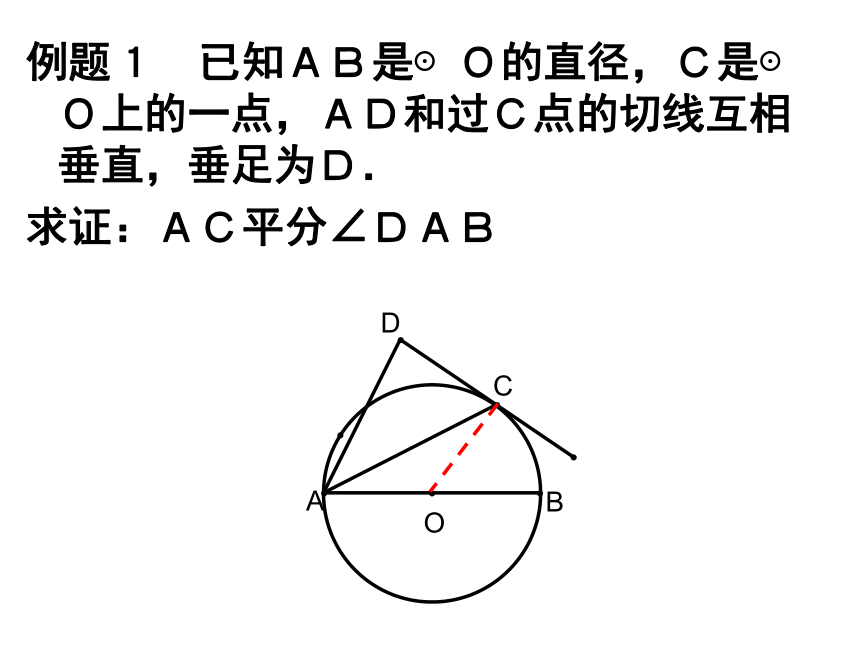
则AC ABC直径切点A⊥例题1 已知AB是⊙O的直径,C是⊙O上的一点,AD和过C点的切线互相垂直,垂足为D.
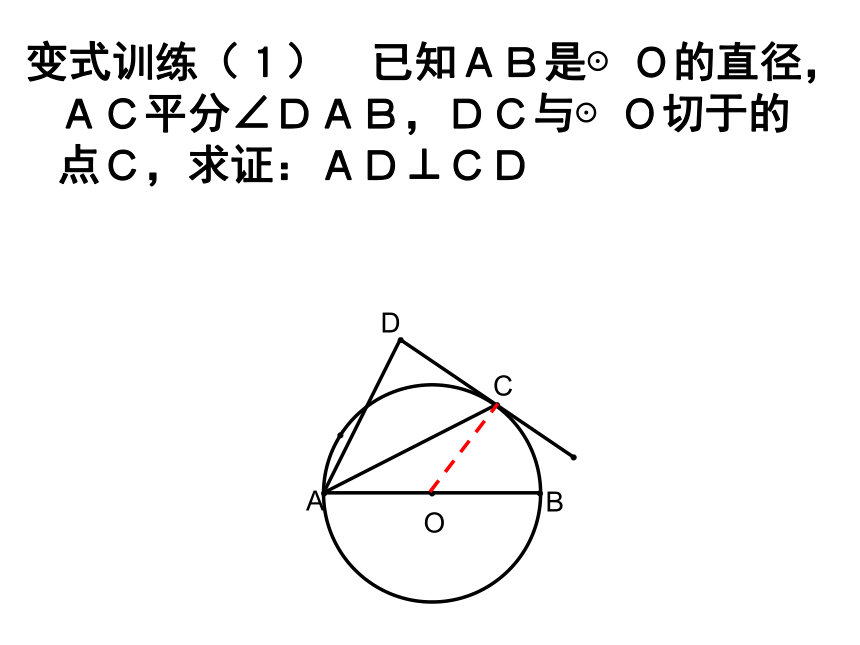
求证:AC平分∠DAB变式训练(1) 已知AB是⊙O的直径,AC平分∠DAB,DC与⊙O切于的点C,求证:AD⊥CD变式训练(2)如图,AB是⊙O的直径,,CD与⊙O切于点C,AD⊥CD于D,BC、AD的延长线交于点E,且AE=BE,求∠A的度数。c变式训练(3)如图,AB是⊙O的直径,CD与⊙O切于点C,AD⊥CD于D,延长DC交AB的延长线于F,且BF=3,AF=9,求DF的长。
以直角三角形ABC的直角边AB为直径作圆交斜边AC于点D,过点D作半圆的切线交BC于点E,求证:OE∥AC例题2 如图,已知:AB是⊙O的直径,BC为⊙O的切线,切点为B,OC平行于弦AD,求证:DC是⊙O的切线.变式训练(1) 如图,已知:BC,CD是⊙O的切线,切点分别是B,D,
求证:AD∥OC变式训练(2) 在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E,求证:CD是小圆的切线。FoAFBPCEO变式训练(3)如图,已知:PA是∠ BAC的角的平分线,AB切⊙O与点E。
求证:AC是⊙O的切线.
如图,AB是⊙O的直径,DE是⊙O的切线,⊙O过BC的中点D
求证:DE⊥AC
作业
教材:P110页第4题
P131页第4题
二是 。 经过半径的外端垂直于这条半径∵l过半径OA的外端A且OA⊥l
∴l是⊙O的切线议一议如果AB是⊙O的切线,切点为A,那么半径OA与直线AB是不是一定垂直呢?一定垂直切线的性质定理:圆的切线垂直于过切点的半径即:∵直线AB是⊙O的切线, A为切点
∴AB⊥OA (圆的切线垂直于过切点的半径)切线的性质切线与圆有 公共点;
圆心到直线的距离等于 。
切线垂直于 的半径。
经过圆心且垂直于切线的直线必过 。
过切点且垂直于切线的直线必过 。唯一圆的半径过切点切点圆心如图,(1)AB切⊙O于A点,AC⊥AB,则AC是⊙O的 。
(2)AB切⊙O于A点,OC⊥AB,则CO的延长线经过 。
(3)若AB切⊙O于点A,AC是⊙O的直径,
则AC ABC直径切点A⊥例题1 已知AB是⊙O的直径,C是⊙O上的一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB变式训练(1) 已知AB是⊙O的直径,AC平分∠DAB,DC与⊙O切于的点C,求证:AD⊥CD变式训练(2)如图,AB是⊙O的直径,,CD与⊙O切于点C,AD⊥CD于D,BC、AD的延长线交于点E,且AE=BE,求∠A的度数。c变式训练(3)如图,AB是⊙O的直径,CD与⊙O切于点C,AD⊥CD于D,延长DC交AB的延长线于F,且BF=3,AF=9,求DF的长。
以直角三角形ABC的直角边AB为直径作圆交斜边AC于点D,过点D作半圆的切线交BC于点E,求证:OE∥AC例题2 如图,已知:AB是⊙O的直径,BC为⊙O的切线,切点为B,OC平行于弦AD,求证:DC是⊙O的切线.变式训练(1) 如图,已知:BC,CD是⊙O的切线,切点分别是B,D,
求证:AD∥OC变式训练(2) 在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E,求证:CD是小圆的切线。FoAFBPCEO变式训练(3)如图,已知:PA是∠ BAC的角的平分线,AB切⊙O与点E。
求证:AC是⊙O的切线.
如图,AB是⊙O的直径,DE是⊙O的切线,⊙O过BC的中点D
求证:DE⊥AC
作业
教材:P110页第4题
P131页第4题
同课章节目录
