4.1 单位圆与任意角的正弦函数、余弦函数定义 课件(共40张PPT)-2024-2025学年高一下学期数学北师大版(2019)必修第二册
文档属性
| 名称 | 4.1 单位圆与任意角的正弦函数、余弦函数定义 课件(共40张PPT)-2024-2025学年高一下学期数学北师大版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 00:00:00 | ||
图片预览







文档简介
(共40张PPT)
第4小节 正弦函数与余弦函数的概念及性质
学习目标
1.4.1 单位圆与任意角的三角函数意义
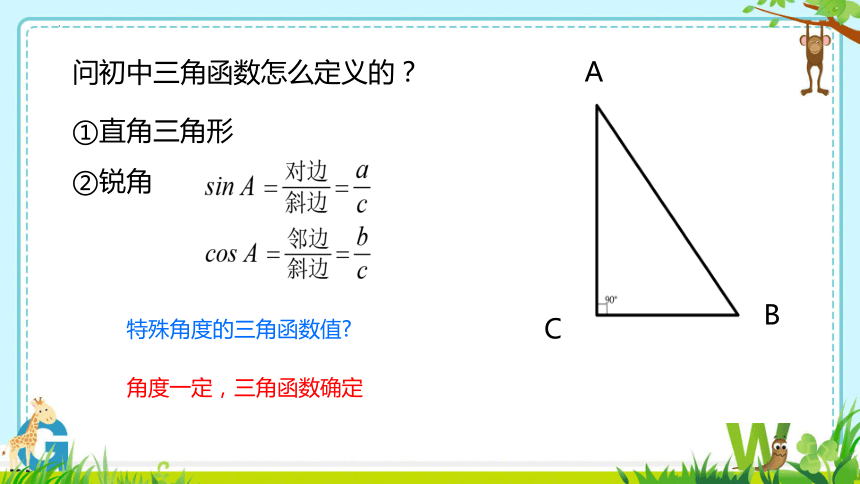
问初中三角函数怎么定义的?
①直角三角形
②锐角
A
B
C
特殊角度的三角函数值
角度一定,三角函数确定
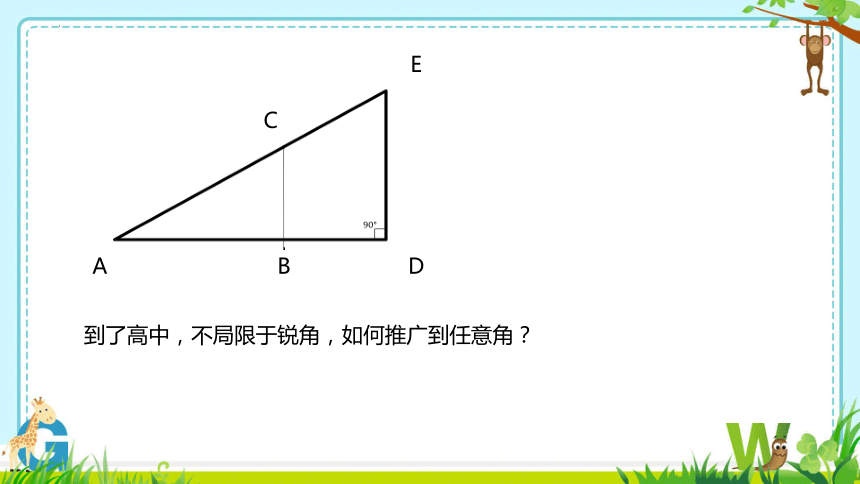
A
B
C
D
E
到了高中,不局限于锐角,如何推广到任意角?
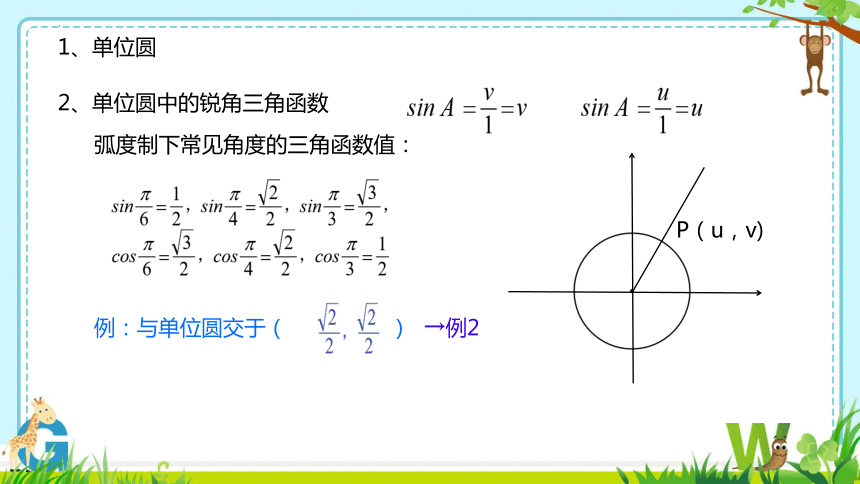
1、单位圆
2、单位圆中的锐角三角函数
弧度制下常见角度的三角函数值:
P(u,v)
例:与单位圆交于( )
→例2
3、单位圆中的任意角的三角函数
P(u,v)
(0,1)
(-1,0)
例:与单位圆交于
纵坐标
横坐标
思考:当半径不为1时,怎么定义?
注意:①和横、纵坐标相关,且唯一确定
②有正有负
总结:
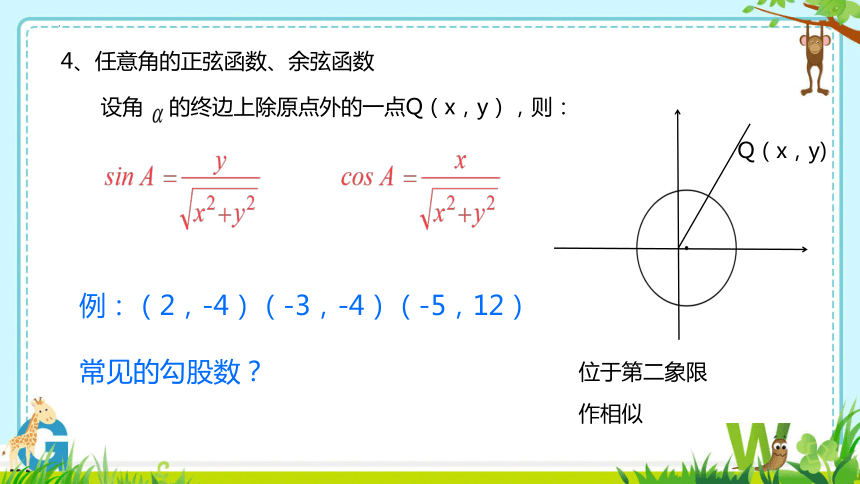
4、任意角的正弦函数、余弦函数
设角 的终边上除原点外的一点Q(x,y),则:
Q(x,y)
例:(2,-4)(-3,-4)(-5,12)
常见的勾股数?
作相似
位于第二象限
题型1:
(求任意角的正弦函数值、余弦函数值)
练习1~2
典例1
练习1
题型2:
(确定三角函数值的符号)
典例2
练习2
能力提升:
1.4.2 单位圆与正弦函数、余弦函数的性质
函数!
P(u,v)
自变量:α
应变量:sin α,cosα
α
思考:与半径是否相关?
性质1:定义域:R
性质2:最大(小)值,值域:1,-1,[-1,1]
P(u,v)
α
性质3:周期性
性质4:单调性
性质5:符号
T=2kΠ,k∈Z
sinα的单增区间:
单减区间:
cosα的单增区间:
单减区间:
题型1:
(给定范围,据单位圆求三角函数的值域、最值、单调区间)
练习
题型2:
(求三角函数的定义域)
典例1
题型3:
(判断符号求值)
典例2:(1)确定 sin105°·cos230°的符号
(2)求值:sin(-1740°)cos1470°+cos(-660°)·sin 750°
题型4:
(三角函数在单位圆中的妙用)
典例3
1.4.3 诱导公式与对称
疑问:为什么叫“诱导公式”呢?
induction formula
学习目标
1、了解正弦函数、余弦函数的诱导公式的意义和作用
2、根据角的终边的对称关系,推导并掌握对应的诱导公式
化繁为简
奇变偶不变,符号看象限
1、终边相同的角的三角函数值__________
相等
P(u,v)
α
引例
2、由特殊角的终边对称关系诱导
①角-α 与角α的终边关于____________对称
P(u,v)
α
-α
结论1:
结论2:
P1(u,-v)
x轴
②角 与角α的终边关于____________对称
P(u,v)
α
结论:
原点
补充:角 与角α
③角 与角α的终边关于____________对称
P(u,v)
α
结论:
y轴
当a为第一象限角时
练习1
题型总结:
1、运用诱导公式求值
2、运用诱导公式化简
练习2:计算
拓展:(易错题型)
化简
1.4.4 诱导公式与旋转
1、根据角的终边的旋转关系,推导并掌握2组诱导公式
学习目标
2、对所有诱导公式进行综合应用
P(u,v)
α
角 与角α的三角函数值关系:
1、
2、学会运用口诀“奇变偶不变,符号看象限”
第4小节 正弦函数与余弦函数的概念及性质
学习目标
1.4.1 单位圆与任意角的三角函数意义
问初中三角函数怎么定义的?
①直角三角形
②锐角
A
B
C
特殊角度的三角函数值
角度一定,三角函数确定
A
B
C
D
E
到了高中,不局限于锐角,如何推广到任意角?
1、单位圆
2、单位圆中的锐角三角函数
弧度制下常见角度的三角函数值:
P(u,v)
例:与单位圆交于( )
→例2
3、单位圆中的任意角的三角函数
P(u,v)
(0,1)
(-1,0)
例:与单位圆交于
纵坐标
横坐标
思考:当半径不为1时,怎么定义?
注意:①和横、纵坐标相关,且唯一确定
②有正有负
总结:
4、任意角的正弦函数、余弦函数
设角 的终边上除原点外的一点Q(x,y),则:
Q(x,y)
例:(2,-4)(-3,-4)(-5,12)
常见的勾股数?
作相似
位于第二象限
题型1:
(求任意角的正弦函数值、余弦函数值)
练习1~2
典例1
练习1
题型2:
(确定三角函数值的符号)
典例2
练习2
能力提升:
1.4.2 单位圆与正弦函数、余弦函数的性质
函数!
P(u,v)
自变量:α
应变量:sin α,cosα
α
思考:与半径是否相关?
性质1:定义域:R
性质2:最大(小)值,值域:1,-1,[-1,1]
P(u,v)
α
性质3:周期性
性质4:单调性
性质5:符号
T=2kΠ,k∈Z
sinα的单增区间:
单减区间:
cosα的单增区间:
单减区间:
题型1:
(给定范围,据单位圆求三角函数的值域、最值、单调区间)
练习
题型2:
(求三角函数的定义域)
典例1
题型3:
(判断符号求值)
典例2:(1)确定 sin105°·cos230°的符号
(2)求值:sin(-1740°)cos1470°+cos(-660°)·sin 750°
题型4:
(三角函数在单位圆中的妙用)
典例3
1.4.3 诱导公式与对称
疑问:为什么叫“诱导公式”呢?
induction formula
学习目标
1、了解正弦函数、余弦函数的诱导公式的意义和作用
2、根据角的终边的对称关系,推导并掌握对应的诱导公式
化繁为简
奇变偶不变,符号看象限
1、终边相同的角的三角函数值__________
相等
P(u,v)
α
引例
2、由特殊角的终边对称关系诱导
①角-α 与角α的终边关于____________对称
P(u,v)
α
-α
结论1:
结论2:
P1(u,-v)
x轴
②角 与角α的终边关于____________对称
P(u,v)
α
结论:
原点
补充:角 与角α
③角 与角α的终边关于____________对称
P(u,v)
α
结论:
y轴
当a为第一象限角时
练习1
题型总结:
1、运用诱导公式求值
2、运用诱导公式化简
练习2:计算
拓展:(易错题型)
化简
1.4.4 诱导公式与旋转
1、根据角的终边的旋转关系,推导并掌握2组诱导公式
学习目标
2、对所有诱导公式进行综合应用
P(u,v)
α
角 与角α的三角函数值关系:
1、
2、学会运用口诀“奇变偶不变,符号看象限”
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
