4.4.2 对数函数的图象和性质 课件(共17张PPT)-2024-2025学年高一上学期数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.4.2 对数函数的图象和性质 课件(共17张PPT)-2024-2025学年高一上学期数学人教A版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 12:50:58 | ||
图片预览






文档简介
(共17张PPT)
4.4.2 对数函数的图象和性质
函数大单元——幂函数、指数函数、对数函数
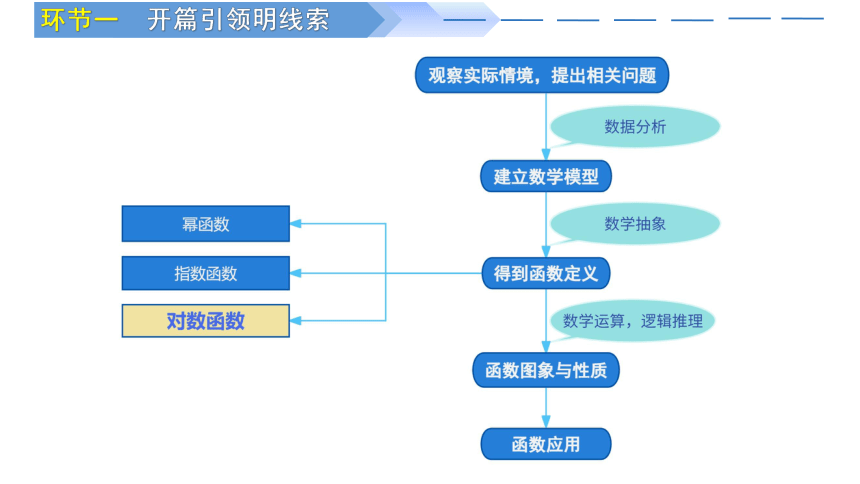
环节一 开篇引领明线索
环节二 探究合作现新知
探究任务一 画对数函数的图象
探究任务二 总结归纳对数函数的性质
【问题1】 指数函数图象和性质的研究方法与过程?
类比指数函数
思考:在探究任务一的研究和展示过程中,你有什么体会?
请完成自评与互评表。
环节二 探究合作现新知
环节三 类比概括得性质
探究任务二 总结归纳对数函数的性质
图像特征
函数性质
【问题2】 能否从函数解析式上对性质进行再解释?
环节三 类比概括得性质
【问题3】 对数函数中的变化对函数图象的位置有何影响?
环节三 类比概括得性质
y=2x
x∈R ,
y∈(0,+∞)
x=log2y
y=log2x
x∈(0,+∞)
y∈R
对数函数y=log2x(x∈(0,+∞))与指数函数y=2x (x∈R)互为反函数.
环节四:拾级而上拓认知
环节四 拾级而上拓认知
环节四 拾级而上拓认知
【问题4】 对数函数 与指数函数 是否互为反函数?
例3 比较下列各题中两个值的大小:
(1) log23.4, log28.5
(2) log 0.3 1.8, log 0.3 2.7
(3) loga5.1, loga5.9 (a>0,且a ≠1)
(5) log3 7与 log5 6
【问题5】根据以上经验,请你说说如何比较两个对数式的大小
环节五 深度学习提素养
溶液酸碱度是通过pH计量的. 在化学中,pH的大小可以通过pH试纸进行测量,pH的计算公式为pH= - lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升.
(1)根据对数函数性质及上述pH的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2)已知纯净水中氢离子的浓度为[H+]=10-7摩尔/升,计算纯净水的pH.
(3)纯净水的PH值一般在5.0~7.0之间,求在此范围内纯净水中氢离子的浓度?
情境问题探究
环节五 深度学习提素养
天文领域:火箭速度
地理领域:里氏地震等级
物理领域:
测量声音
分贝
环节五 深度学习提素养
本课小结
环节六 课堂总结精认知
1、知识内容
对数函数图象、性质.
2 、思想方法
(1) 数形结合:
由解析式到图象——由数到形, 以形读数;
由图象到性质—— 由形到数, 以数观形;
(2) 分类讨论:底数的两个范围对单调性的影响。
(3) 类比 :指数与对数函数不仅在概念、图象与性质上有联系,在解决问题的类型上也有联系,要将两者作为一个整体学习与应用。
(4) 特殊到一般
思考:通过本节课的学习,你有哪些收获?
本课小结
环节六 课堂总结精认知
幂、指、对函数展现了指数与幂次之间微妙而又紧密的联系。
指数函数与对数函数之间存在着一种逆关系——互为反函数,而幂函数作为更一般化的存在,在一定程度上包含了指数函数和对数函数的某些特性。
这些函数教会我们在变化中寻找规律,在复杂中提炼简洁,让我们以更加敏锐的洞察力和坚韧的毅力去攀登数学的高峰。
环节七 课后作业促发展
根据课上学习的情况,完成探究活动和过程性评价表(及时反思,利于调整)
【基础作业】
教材135页练习;140页2,3,4题.
【能力作业】
1.比较log 6,log 7,log 14 的大小;2.证明对数函数的单调性.
【探究作业】
现实生活中,有很多“对数函数”模型的例子,请同学们课后查阅
资料,探究对数函数相关模型.
4.4.2 对数函数的图象和性质
函数大单元——幂函数、指数函数、对数函数
环节一 开篇引领明线索
环节二 探究合作现新知
探究任务一 画对数函数的图象
探究任务二 总结归纳对数函数的性质
【问题1】 指数函数图象和性质的研究方法与过程?
类比指数函数
思考:在探究任务一的研究和展示过程中,你有什么体会?
请完成自评与互评表。
环节二 探究合作现新知
环节三 类比概括得性质
探究任务二 总结归纳对数函数的性质
图像特征
函数性质
【问题2】 能否从函数解析式上对性质进行再解释?
环节三 类比概括得性质
【问题3】 对数函数中的变化对函数图象的位置有何影响?
环节三 类比概括得性质
y=2x
x∈R ,
y∈(0,+∞)
x=log2y
y=log2x
x∈(0,+∞)
y∈R
对数函数y=log2x(x∈(0,+∞))与指数函数y=2x (x∈R)互为反函数.
环节四:拾级而上拓认知
环节四 拾级而上拓认知
环节四 拾级而上拓认知
【问题4】 对数函数 与指数函数 是否互为反函数?
例3 比较下列各题中两个值的大小:
(1) log23.4, log28.5
(2) log 0.3 1.8, log 0.3 2.7
(3) loga5.1, loga5.9 (a>0,且a ≠1)
(5) log3 7与 log5 6
【问题5】根据以上经验,请你说说如何比较两个对数式的大小
环节五 深度学习提素养
溶液酸碱度是通过pH计量的. 在化学中,pH的大小可以通过pH试纸进行测量,pH的计算公式为pH= - lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升.
(1)根据对数函数性质及上述pH的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2)已知纯净水中氢离子的浓度为[H+]=10-7摩尔/升,计算纯净水的pH.
(3)纯净水的PH值一般在5.0~7.0之间,求在此范围内纯净水中氢离子的浓度?
情境问题探究
环节五 深度学习提素养
天文领域:火箭速度
地理领域:里氏地震等级
物理领域:
测量声音
分贝
环节五 深度学习提素养
本课小结
环节六 课堂总结精认知
1、知识内容
对数函数图象、性质.
2 、思想方法
(1) 数形结合:
由解析式到图象——由数到形, 以形读数;
由图象到性质—— 由形到数, 以数观形;
(2) 分类讨论:底数的两个范围对单调性的影响。
(3) 类比 :指数与对数函数不仅在概念、图象与性质上有联系,在解决问题的类型上也有联系,要将两者作为一个整体学习与应用。
(4) 特殊到一般
思考:通过本节课的学习,你有哪些收获?
本课小结
环节六 课堂总结精认知
幂、指、对函数展现了指数与幂次之间微妙而又紧密的联系。
指数函数与对数函数之间存在着一种逆关系——互为反函数,而幂函数作为更一般化的存在,在一定程度上包含了指数函数和对数函数的某些特性。
这些函数教会我们在变化中寻找规律,在复杂中提炼简洁,让我们以更加敏锐的洞察力和坚韧的毅力去攀登数学的高峰。
环节七 课后作业促发展
根据课上学习的情况,完成探究活动和过程性评价表(及时反思,利于调整)
【基础作业】
教材135页练习;140页2,3,4题.
【能力作业】
1.比较log 6,log 7,log 14 的大小;2.证明对数函数的单调性.
【探究作业】
现实生活中,有很多“对数函数”模型的例子,请同学们课后查阅
资料,探究对数函数相关模型.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
