2.1 角的概念推广 课件(共23张PPT)-2024-2025学年高一下学期数学北师大版(2019)必修第二册
文档属性
| 名称 | 2.1 角的概念推广 课件(共23张PPT)-2024-2025学年高一下学期数学北师大版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 12:51:41 | ||
图片预览






文档简介
(共23张PPT)
2.任意角
第一章 三角函数
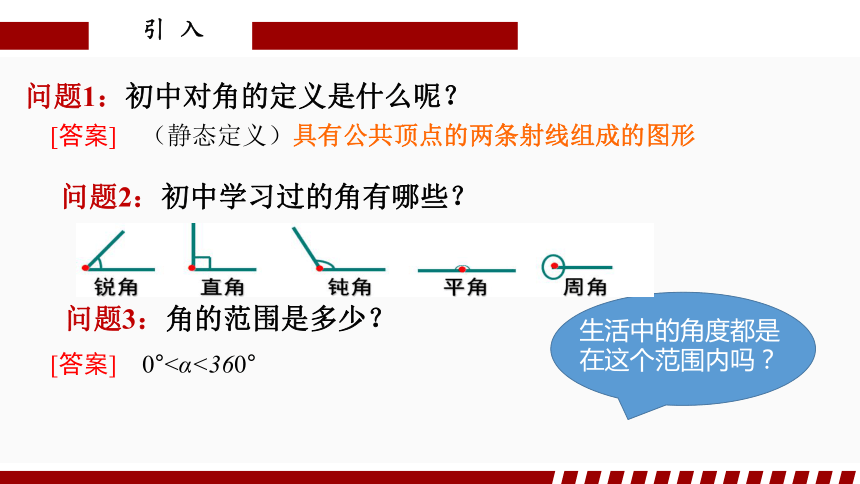
那些年,我们一起学过的角是如何定义的?
引 入
问题1:初中对角的定义是什么呢?
[答案] 0°<α<360°
生活中的角度都是在这个范围内吗?
[答案] (静态定义)具有公共顶点的两条射线组成的图形
问题2:初中学习过的角有哪些?
问题3:角的范围是多少?
引 入
问题4:在现实生活中有没有不在 范围内的角?
比如跳水和体操运动中的“向前翻腾四周半抱膝3.5”、“前空翻转体750°”、
“后空翻转体540° ”等
引 入
时钟从12:00到14:00,分针转过了多少度?
齿轮旋转形成的角
引 入
发现:角是由“旋转”而来!
你发现了什么?
探究新知
点O 叫做角α的顶点,
射线OA叫做角α的始边,
射线OB叫做角α的终边.
①定义:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.
问题5:用旋转来描述角,需要考虑什么?
旋转中心、旋转方向和旋转量
1.角的概念
“旋转”形成角
O
顶点
始边
终边
A
B
探究新知
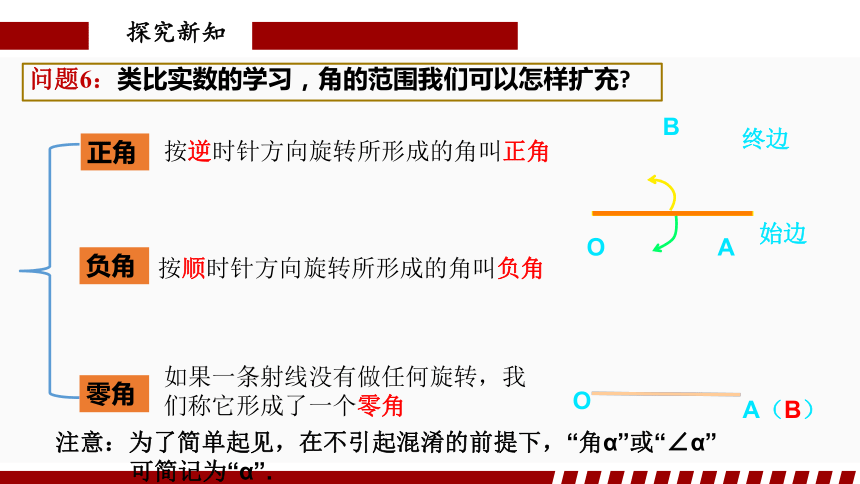
问题6:类比实数的学习,角的范围我们可以怎样扩充
正角
负角
零角
按逆时针方向旋转所形成的角叫正角
按顺时针方向旋转所形成的角叫负角
如果一条射线没有做任何旋转,我们称它形成了一个零角
始边
终边
O
A
B
A(B)
O
注意:为了简单起见,在不引起混淆的前提下,“角α”或“∠α”
可简记为“α”.
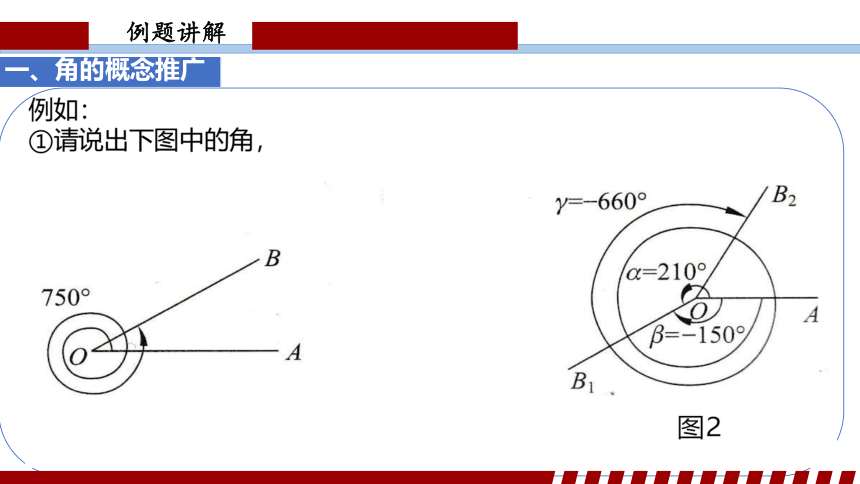
一、角的概念推广
例题讲解
课堂练习
1.将射线OM绕端点O按逆时针方向旋转120°所得的角为( )
A.120° B.-120°
C.60° D.240°
A
2.时钟1小时,时针转动的角为( )
A.30° B.-30°
C.60° D.-60°
B
探究新知
为了进一步研究角的需要,我们常在直角坐标系内讨论角,
2.象限角
角的顶点与坐标原点重合,
角的始边与x轴的非负半轴重合.
y
x
O
角的终边
角的始边
终边落在第几象限就是第几象限角
x
y
始边
终边
终边
终边
终边
探究新知
第一象限角:
第二象限角:
第三象限角:
第四象限角:
用集合表示下列各范围的角
象
限
角
探究新知
如果角的终边落在坐标轴上,则该角不属于任何一个象限.
3.轴线角
x
y
始边
终边在坐标轴上的角:
探究新知
y
x
O
角的终边
角的始边
x
y
o
始边
终边
终边
终边
终边
问题7:锐角是第几象限的角?
第一象限的角一定是锐角吗?
第二象限的角一定比第一象限的角大吗?
第三象限角一定是负角吗?
探究新知
4.终边相同的角
动手:在直角坐标系中画出30°,390°,-330°,这些角有什么内在联系?
思考:在直角坐标系中,给定一个角,这个角的终边是否唯一确定?若给一条射线作终边,这个角唯一吗
-330°=30°+(-1)360°
390°=30°+1×360°
{β︱β= 30°+ k·360°,k∈Z}
归纳: 与 30°角终边相同的角
一个角,对应一条终边;
一条终边,对应无数个角:终边相同的角
O
A
30°
相差360°的整数倍
探究新知
{β︱β= 30°+ k·360°, k∈Z}
归纳: 与 30°角终边相同的角
思考: 将30°推广到一般角,结论α应该是什么?
4.终边相同的角
教材P3例题
例题讲解
教材P7练习
课堂检测
课堂练习
在直角坐标系中画出下列角,并指出下面的角是第几象限角?
(1)-50°
(2)405°
(3)210°
(4)-200°
(5)-450°
探究新知
45O
1、用集合表示终边与45o相同的角
2、用集合表示终边落在阴影部分的角
5.区间角
终边落在坐标系的某个区间的角
定边界,定周期
思考: 将45°推广到一般角,结论α应该是什么?
教材P6练习
课堂检测
真
假
假
真
假
真
假
假
教材P7练习
课堂检测
教材P7练习
课堂检测
教材P7练习
课堂检测
2.任意角
第一章 三角函数
那些年,我们一起学过的角是如何定义的?
引 入
问题1:初中对角的定义是什么呢?
[答案] 0°<α<360°
生活中的角度都是在这个范围内吗?
[答案] (静态定义)具有公共顶点的两条射线组成的图形
问题2:初中学习过的角有哪些?
问题3:角的范围是多少?
引 入
问题4:在现实生活中有没有不在 范围内的角?
比如跳水和体操运动中的“向前翻腾四周半抱膝3.5”、“前空翻转体750°”、
“后空翻转体540° ”等
引 入
时钟从12:00到14:00,分针转过了多少度?
齿轮旋转形成的角
引 入
发现:角是由“旋转”而来!
你发现了什么?
探究新知
点O 叫做角α的顶点,
射线OA叫做角α的始边,
射线OB叫做角α的终边.
①定义:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.
问题5:用旋转来描述角,需要考虑什么?
旋转中心、旋转方向和旋转量
1.角的概念
“旋转”形成角
O
顶点
始边
终边
A
B
探究新知
问题6:类比实数的学习,角的范围我们可以怎样扩充
正角
负角
零角
按逆时针方向旋转所形成的角叫正角
按顺时针方向旋转所形成的角叫负角
如果一条射线没有做任何旋转,我们称它形成了一个零角
始边
终边
O
A
B
A(B)
O
注意:为了简单起见,在不引起混淆的前提下,“角α”或“∠α”
可简记为“α”.
一、角的概念推广
例题讲解
课堂练习
1.将射线OM绕端点O按逆时针方向旋转120°所得的角为( )
A.120° B.-120°
C.60° D.240°
A
2.时钟1小时,时针转动的角为( )
A.30° B.-30°
C.60° D.-60°
B
探究新知
为了进一步研究角的需要,我们常在直角坐标系内讨论角,
2.象限角
角的顶点与坐标原点重合,
角的始边与x轴的非负半轴重合.
y
x
O
角的终边
角的始边
终边落在第几象限就是第几象限角
x
y
始边
终边
终边
终边
终边
探究新知
第一象限角:
第二象限角:
第三象限角:
第四象限角:
用集合表示下列各范围的角
象
限
角
探究新知
如果角的终边落在坐标轴上,则该角不属于任何一个象限.
3.轴线角
x
y
始边
终边在坐标轴上的角:
探究新知
y
x
O
角的终边
角的始边
x
y
o
始边
终边
终边
终边
终边
问题7:锐角是第几象限的角?
第一象限的角一定是锐角吗?
第二象限的角一定比第一象限的角大吗?
第三象限角一定是负角吗?
探究新知
4.终边相同的角
动手:在直角坐标系中画出30°,390°,-330°,这些角有什么内在联系?
思考:在直角坐标系中,给定一个角,这个角的终边是否唯一确定?若给一条射线作终边,这个角唯一吗
-330°=30°+(-1)360°
390°=30°+1×360°
{β︱β= 30°+ k·360°,k∈Z}
归纳: 与 30°角终边相同的角
一个角,对应一条终边;
一条终边,对应无数个角:终边相同的角
O
A
30°
相差360°的整数倍
探究新知
{β︱β= 30°+ k·360°, k∈Z}
归纳: 与 30°角终边相同的角
思考: 将30°推广到一般角,结论α应该是什么?
4.终边相同的角
教材P3例题
例题讲解
教材P7练习
课堂检测
课堂练习
在直角坐标系中画出下列角,并指出下面的角是第几象限角?
(1)-50°
(2)405°
(3)210°
(4)-200°
(5)-450°
探究新知
45O
1、用集合表示终边与45o相同的角
2、用集合表示终边落在阴影部分的角
5.区间角
终边落在坐标系的某个区间的角
定边界,定周期
思考: 将45°推广到一般角,结论α应该是什么?
教材P6练习
课堂检测
真
假
假
真
假
真
假
假
教材P7练习
课堂检测
教材P7练习
课堂检测
教材P7练习
课堂检测
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
