广东省深圳市盐田区2024-2025学年八年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 广东省深圳市盐田区2024-2025学年八年级(上)期中数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 571.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 10:31:13 | ||
图片预览


文档简介
2024-2025学年广东省深圳市盐田区八年级(上)期中数学试卷
一、单选题:(每小题只有一个正确选项,每小题3分,共计24分)
1.(3分)实数,,,2π,,|﹣3|,0.313113111…(每两个3之间依次多一个1)中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
2.(3分)如图,已知OA=OB,点A到数轴的距离为1,则数轴上B点所表示的数为( )
A.﹣ B.﹣ C. D.
3.(3分)下列运算正确的是( )
A. B. C. D.
4.(3分)如图,一棵大树被台风刮断,若树在离地面3m处折断,树顶端落在离树底部4m处,则树折断之前高( )
A.5m B.7m C.8m D.10m
5.(3分)对于函数y=﹣2x+3的图象,下列结论错误的是( )
A.图象必经过点(1,1)
B.图象经过第一、二、四象限
C.与x轴的交点为(0,3)
D.若两点A(1,y1),B(3,y2)在该函数图象上,则y1>y2
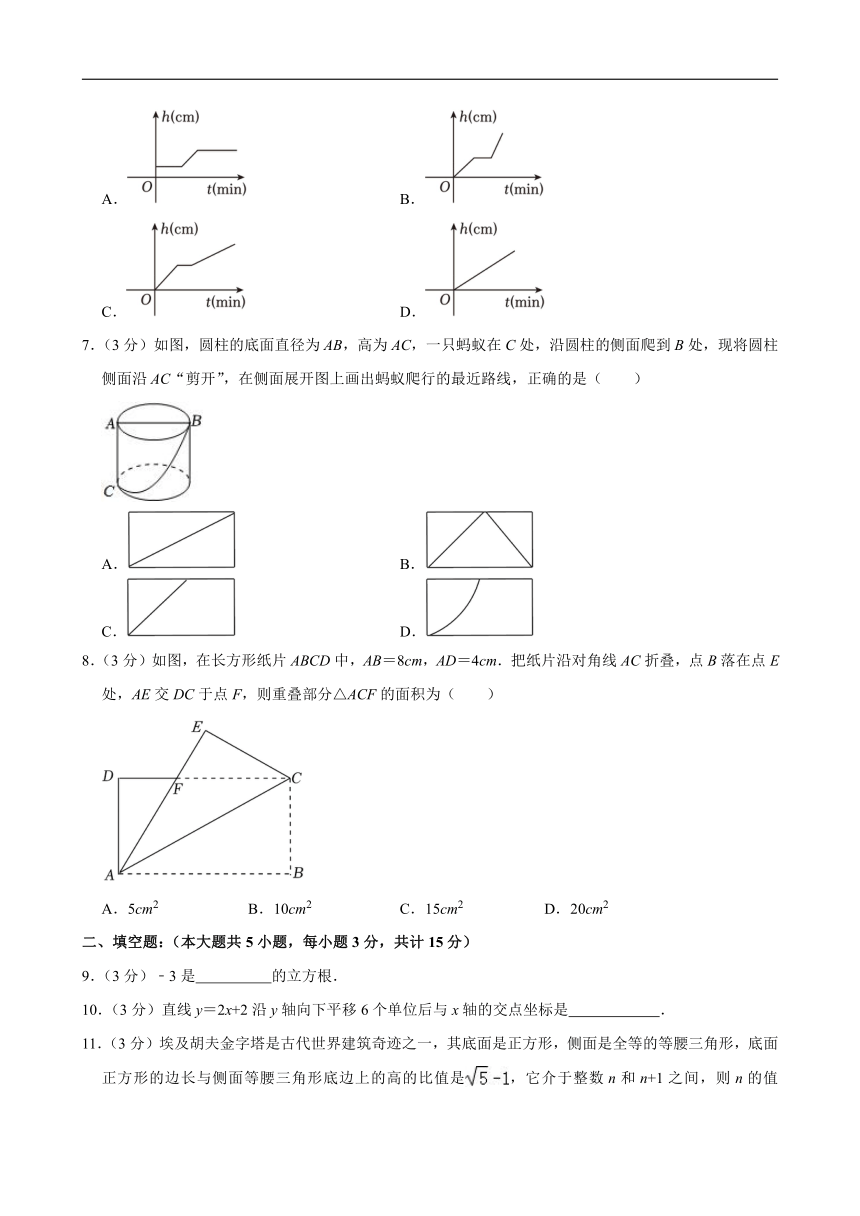
6.(3分)将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内现用一个注水管沿大容器内壁匀速注水,如图,则大圆柱形容器水面的高度h(cm)与注水时间t(min)的函数图象大致( )
A. B.
C. D.
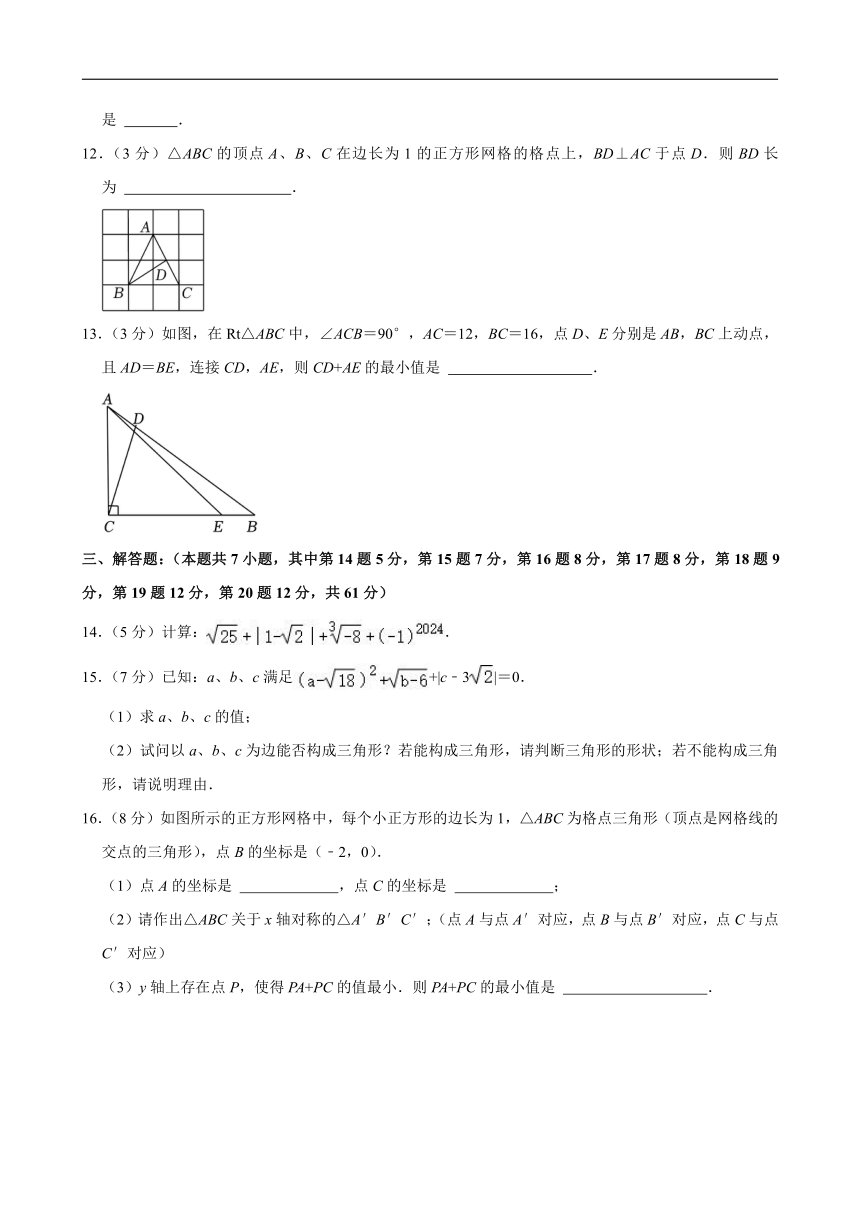
7.(3分)如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A. B.
C. D.
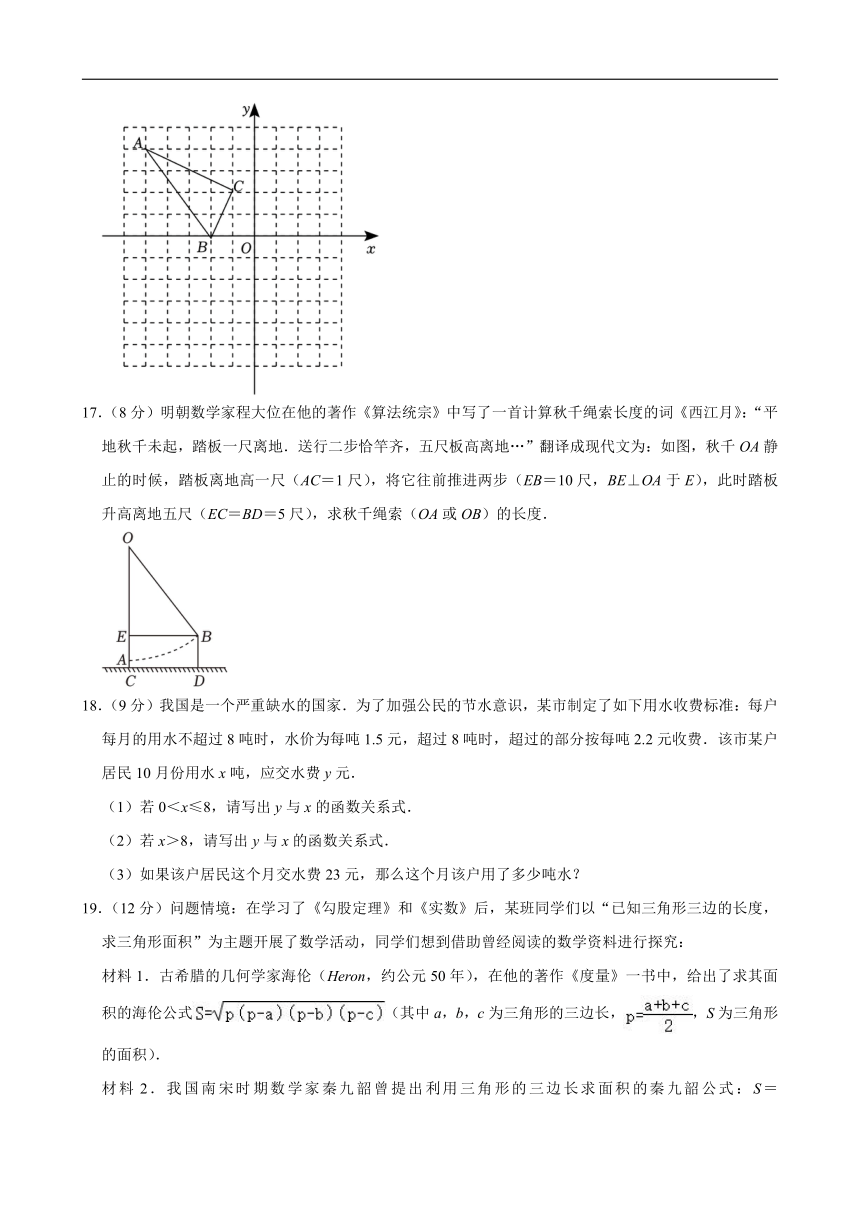
8.(3分)如图,在长方形纸片ABCD中,AB=8cm,AD=4cm.把纸片沿对角线AC折叠,点B落在点E处,AE交DC于点F,则重叠部分△ACF的面积为( )
A.5cm2 B.10cm2 C.15cm2 D.20cm2
二、填空题:(本大题共5小题,每小题3分,共计15分)
9.(3分)﹣3是 的立方根.
10.(3分)直线y=2x+2沿y轴向下平移6个单位后与x轴的交点坐标是 .
11.(3分)埃及胡夫金字塔是古代世界建筑奇迹之一,其底面是正方形,侧面是全等的等腰三角形,底面正方形的边长与侧面等腰三角形底边上的高的比值是,它介于整数n和n+1之间,则n的值是 .
12.(3分)△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D.则BD长为 .
13.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=12,BC=16,点D、E分别是AB,BC上动点,且AD=BE,连接CD,AE,则CD+AE的最小值是 .
三、解答题:(本题共7小题,其中第14题5分,第15题7分,第16题8分,第17题8分,第18题9分,第19题12分,第20题12分,共61分)
14.(5分)计算:.
15.(7分)已知:a、b、c满足+|c﹣3|=0.
(1)求a、b、c的值;
(2)试问以a、b、c为边能否构成三角形?若能构成三角形,请判断三角形的形状;若不能构成三角形,请说明理由.
16.(8分)如图所示的正方形网格中,每个小正方形的边长为1,△ABC为格点三角形(顶点是网格线的交点的三角形),点B的坐标是(﹣2,0).
(1)点A的坐标是 ,点C的坐标是 ;
(2)请作出△ABC关于x轴对称的△A′B′C′;(点A与点A′对应,点B与点B′对应,点C与点C′对应)
(3)y轴上存在点P,使得PA+PC的值最小.则PA+PC的最小值是 .
17.(8分)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地.送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺),将它往前推进两步(EB=10尺,BE⊥OA于E),此时踏板升高离地五尺(EC=BD=5尺),求秋千绳索(OA或OB)的长度.
18.(9分)我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费.该市某户居民10月份用水x吨,应交水费y元.
(1)若0<x≤8,请写出y与x的函数关系式.
(2)若x>8,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费23元,那么这个月该户用了多少吨水?
19.(12分)问题情境:在学习了《勾股定理》和《实数》后,某班同学们以“已知三角形三边的长度,求三角形面积”为主题开展了数学活动,同学们想到借助曾经阅读的数学资料进行探究:
材料1.古希腊的几何学家海伦(Heron,约公元50年),在他的著作《度量》一书中,给出了求其面积的海伦公式(其中a,b,c为三角形的三边长,,S为三角形的面积).
材料2.我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式:S=,其中三角形边长分别为a,b,c,三角形的面积为S.
(1)利用材料1解决下面的问题:当,b=3,时,求这个三角形的面积?
(2)利用材料2解决下面的问题:已知△ABC三条边的长度分别是,,,记△ABC的周长为C△ABC.
①当x=2时,请直接写出△ABC中最长边的长度;
②若x为整数,当C△ABC取得最大值时,请用秦九韶公式求出△ABC的面积.
20.(12分)综合与探究:
如图1,平面直角坐标系中,一次函数图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C,点P是直线AB上的一个动点.
(1)求直线BC的表达式与点C的坐标;
(2)如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
(3)试探究x轴上是否存在点M,使以A,B,M为顶点的三角形是等腰三角形.若存在,直接写出点M的坐标;若不存在,说明理由.
2024-2025学年广东省深圳市盐田区八年级(上)期中数学试卷
参考答案
一、单选题:(每小题只有一个正确选项,每小题3分,共计24分)
1.(3分)实数,,,2π,,|﹣3|,0.313113111…(每两个3之间依次多一个1)中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
选:C.
2.(3分)如图,已知OA=OB,点A到数轴的距离为1,则数轴上B点所表示的数为( )
A.﹣ B.﹣ C. D.
选:A.
3.(3分)下列运算正确的是( )
A. B. C. D.
选:D.
4.(3分)如图,一棵大树被台风刮断,若树在离地面3m处折断,树顶端落在离树底部4m处,则树折断之前高( )
A.5m B.7m C.8m D.10m
选:C.
5.(3分)对于函数y=﹣2x+3的图象,下列结论错误的是( )
A.图象必经过点(1,1)
B.图象经过第一、二、四象限
C.与x轴的交点为(0,3)
D.若两点A(1,y1),B(3,y2)在该函数图象上,则y1>y2
选:C.
6.(3分)将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内现用一个注水管沿大容器内壁匀速注水,如图,则大圆柱形容器水面的高度h(cm)与注水时间t(min)的函数图象大致( )
A. B.
C. D.
选:C.
7.(3分)如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A. B.
C. D.
选:C.
8.(3分)如图,在长方形纸片ABCD中,AB=8cm,AD=4cm.把纸片沿对角线AC折叠,点B落在点E处,AE交DC于点F,则重叠部分△ACF的面积为( )
A.5cm2 B.10cm2 C.15cm2 D.20cm2
选:B.
二、填空题:(本大题共5小题,每小题3分,共计15分)
9.(3分)﹣3是 ﹣27 的立方根.
10.(3分)直线y=2x+2沿y轴向下平移6个单位后与x轴的交点坐标是 (2,0) .
11.(3分)埃及胡夫金字塔是古代世界建筑奇迹之一,其底面是正方形,侧面是全等的等腰三角形,底面正方形的边长与侧面等腰三角形底边上的高的比值是,它介于整数n和n+1之间,则n的值是 1 .
12.(3分)△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D.则BD长为 .
13.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=12,BC=16,点D、E分别是AB,BC上动点,且AD=BE,连接CD,AE,则CD+AE的最小值是 4 .
三、解答题:(本题共7小题,其中第14题5分,第15题7分,第16题8分,第17题8分,第18题9分,第19题12分,第20题12分,共61分)
14.(5分)计算:.
【解答】解:原式=
=
=.
15.(7分)已知:a、b、c满足+|c﹣3|=0.
(1)求a、b、c的值;
(2)试问以a、b、c为边能否构成三角形?若能构成三角形,请判断三角形的形状;若不能构成三角形,请说明理由.
【解答】解:(1)∵,
∴,b﹣6=0,,
∴,b=6,;
(2)∵1<2<9,
∴,即,
∴,
∴以a、b、c为边能构成三角形,
∵,b=6,
∴a2+c2=b2,
∴三角形的形状是等腰直角三角形.
16.(8分)如图所示的正方形网格中,每个小正方形的边长为1,△ABC为格点三角形(顶点是网格线的交点的三角形),点B的坐标是(﹣2,0).
(1)点A的坐标是 (﹣5,4) ,点C的坐标是 (﹣1,2) ;
(2)请作出△ABC关于x轴对称的△A′B′C′;(点A与点A′对应,点B与点B′对应,点C与点C′对应)
(3)y轴上存在点P,使得PA+PC的值最小.则PA+PC的最小值是 .
【解答】解:(1)由图可得,A(﹣5,4),C(﹣1,2).
故答案为:(﹣5,4);(﹣1,2).
(2)如图,△A′B′C′即为所求.
(3)取点C关于y轴的对称点C'',连接AC''交y轴于点P,连接CP,
此时PA+PC=PA+PC''=AC'',为最小值,
由勾股定理得,AC''==,
∴PA+PC的最小值是.
故答案为:.
17.(8分)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地.送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺),将它往前推进两步(EB=10尺,BE⊥OA于E),此时踏板升高离地五尺(EC=BD=5尺),求秋千绳索(OA或OB)的长度.
【解答】解:设OA=OB=x尺,
∵EC=BD=5尺,AC=1尺,
∴EA=EC﹣AC=5﹣1=4(尺),OE=OA﹣AE=(x﹣4)尺,
在Rt△OEB中,OE=(x﹣4)尺,OB=x尺,EB=10尺,
根据勾股定理得:x2=(x﹣4)2+102,
整理得:8x=116,
即2x=29,
解得:x=14.5,
则秋千绳索的长度为14.5尺.
18.(9分)我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费.该市某户居民10月份用水x吨,应交水费y元.
(1)若0<x≤8,请写出y与x的函数关系式.
(2)若x>8,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费23元,那么这个月该户用了多少吨水?
【解答】解:(1)根据题意可知:
当0<x≤8时,y=1.5x;
(2)根据题意可知:
当x>8时,y=1.5×8+2.2×(x﹣8)=2.2x﹣5.6;
(3)∵当0<x≤8时,y=1.5x,
y的最大值为1.5×8=12(元),12<23,
∴该户当月用水超过8吨.
令y=2.2x﹣5.6中y=23,则23=2.2x﹣5.6,
解得:x=13.
答:这个月该户用了13吨水.
19.(12分)问题情境:在学习了《勾股定理》和《实数》后,某班同学们以“已知三角形三边的长度,求三角形面积”为主题开展了数学活动,同学们想到借助曾经阅读的数学资料进行探究:
材料1.古希腊的几何学家海伦(Heron,约公元50年),在他的著作《度量》一书中,给出了求其面积的海伦公式(其中a,b,c为三角形的三边长,,S为三角形的面积).
材料2.我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式:S=,其中三角形边长分别为a,b,c,三角形的面积为S.
(1)利用材料1解决下面的问题:当,b=3,时,求这个三角形的面积?
(2)利用材料2解决下面的问题:已知△ABC三条边的长度分别是,,,记△ABC的周长为C△ABC.
①当x=2时,请直接写出△ABC中最长边的长度;
②若x为整数,当C△ABC取得最大值时,请用秦九韶公式求出△ABC的面积.
【解答】解:(1)当,b=3,时,==,
∴p﹣a=﹣=,
p﹣b=﹣3=,
p﹣c=﹣2=,
∴p(p﹣a)(p﹣b)(p﹣c)=×××=×=9×1=9,
∴==3,
∴三角形的面积为3;
(2)①当x=2时,
=,=3,=4﹣()2=4﹣2=2,
故△ABC中最长边的长度为3;
②∵x+1≥0,4﹣x≥0,
∴﹣1≤x≤4.
∵4﹣()2=4﹣(4﹣x)=x,三角形的边为正值,
∴x>0,
∴0<x≤4.
∴=5﹣x,4﹣()2=4﹣(4﹣x)=x,
∴C△ABC=++
=+5﹣x+x
=+5,
∵C△ABC=+5(﹣1≤x≤4),且x为整数,
当x=4时,三边为,1,4,
∵+1<4,
∴不合题意舍去,
当x=3时,三边为2,2,3,
∴C△ABC=2+2+3=7,
∴S△ABC=
=
=
=.
∴△ABC的面积为.
20.(12分)综合与探究:
如图1,平面直角坐标系中,一次函数图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C,点P是直线AB上的一个动点.
(1)求直线BC的表达式与点C的坐标;
(2)如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
(3)试探究x轴上是否存在点M,使以A,B,M为顶点的三角形是等腰三角形.若存在,直接写出点M的坐标;若不存在,说明理由.
【解答】解:(1)令y=0,则x+3=0,
∴x=﹣6,
∴A(﹣6,0),
令x=0,则y=3,
∴B(0,3),
∵一次函数y=﹣x+b的图象经过点B,
∴b=3,
∴y=﹣x+3,
令y=0,则x=3,
∴C(3,0);
(2)存在,理由如下:
设P(t,t+3),则Q(t,﹣t+3),
∴PQ=|t|,
∵B(0,3),C(3,0),
∴BC=3,
∵PQ=BC,
∴|t|=3,
∴t=2或t=﹣2,
∴P(2,+3)或P(﹣2,﹣+3);
(3)存在,理由如下:
∵A(﹣6,0),B(0,3),
∴AB=3,
①当以A为等腰三角形的顶点时,
AB=AM=3,
∴M(﹣6+3,0)或(﹣6﹣3,0);
②当以B为等腰三角形的顶点时,
AB=BM,
∴M点与A点关于y轴对称,
∴M(6,0);
③当以M为等腰三角形的顶点时,
MA=MB,
设M(m,0),
∴(m+6)2=m2+9,
∴m=﹣,
∴M(﹣,0);
综上所述:M点的坐标为(﹣6+3,0)或(﹣6﹣3,0)或(6,0)或(﹣,0).
一、单选题:(每小题只有一个正确选项,每小题3分,共计24分)
1.(3分)实数,,,2π,,|﹣3|,0.313113111…(每两个3之间依次多一个1)中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
2.(3分)如图,已知OA=OB,点A到数轴的距离为1,则数轴上B点所表示的数为( )
A.﹣ B.﹣ C. D.
3.(3分)下列运算正确的是( )
A. B. C. D.
4.(3分)如图,一棵大树被台风刮断,若树在离地面3m处折断,树顶端落在离树底部4m处,则树折断之前高( )
A.5m B.7m C.8m D.10m
5.(3分)对于函数y=﹣2x+3的图象,下列结论错误的是( )
A.图象必经过点(1,1)
B.图象经过第一、二、四象限
C.与x轴的交点为(0,3)
D.若两点A(1,y1),B(3,y2)在该函数图象上,则y1>y2
6.(3分)将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内现用一个注水管沿大容器内壁匀速注水,如图,则大圆柱形容器水面的高度h(cm)与注水时间t(min)的函数图象大致( )
A. B.
C. D.
7.(3分)如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A. B.
C. D.
8.(3分)如图,在长方形纸片ABCD中,AB=8cm,AD=4cm.把纸片沿对角线AC折叠,点B落在点E处,AE交DC于点F,则重叠部分△ACF的面积为( )
A.5cm2 B.10cm2 C.15cm2 D.20cm2
二、填空题:(本大题共5小题,每小题3分,共计15分)
9.(3分)﹣3是 的立方根.
10.(3分)直线y=2x+2沿y轴向下平移6个单位后与x轴的交点坐标是 .
11.(3分)埃及胡夫金字塔是古代世界建筑奇迹之一,其底面是正方形,侧面是全等的等腰三角形,底面正方形的边长与侧面等腰三角形底边上的高的比值是,它介于整数n和n+1之间,则n的值是 .
12.(3分)△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D.则BD长为 .
13.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=12,BC=16,点D、E分别是AB,BC上动点,且AD=BE,连接CD,AE,则CD+AE的最小值是 .
三、解答题:(本题共7小题,其中第14题5分,第15题7分,第16题8分,第17题8分,第18题9分,第19题12分,第20题12分,共61分)
14.(5分)计算:.
15.(7分)已知:a、b、c满足+|c﹣3|=0.
(1)求a、b、c的值;
(2)试问以a、b、c为边能否构成三角形?若能构成三角形,请判断三角形的形状;若不能构成三角形,请说明理由.
16.(8分)如图所示的正方形网格中,每个小正方形的边长为1,△ABC为格点三角形(顶点是网格线的交点的三角形),点B的坐标是(﹣2,0).
(1)点A的坐标是 ,点C的坐标是 ;
(2)请作出△ABC关于x轴对称的△A′B′C′;(点A与点A′对应,点B与点B′对应,点C与点C′对应)
(3)y轴上存在点P,使得PA+PC的值最小.则PA+PC的最小值是 .
17.(8分)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地.送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺),将它往前推进两步(EB=10尺,BE⊥OA于E),此时踏板升高离地五尺(EC=BD=5尺),求秋千绳索(OA或OB)的长度.
18.(9分)我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费.该市某户居民10月份用水x吨,应交水费y元.
(1)若0<x≤8,请写出y与x的函数关系式.
(2)若x>8,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费23元,那么这个月该户用了多少吨水?
19.(12分)问题情境:在学习了《勾股定理》和《实数》后,某班同学们以“已知三角形三边的长度,求三角形面积”为主题开展了数学活动,同学们想到借助曾经阅读的数学资料进行探究:
材料1.古希腊的几何学家海伦(Heron,约公元50年),在他的著作《度量》一书中,给出了求其面积的海伦公式(其中a,b,c为三角形的三边长,,S为三角形的面积).
材料2.我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式:S=,其中三角形边长分别为a,b,c,三角形的面积为S.
(1)利用材料1解决下面的问题:当,b=3,时,求这个三角形的面积?
(2)利用材料2解决下面的问题:已知△ABC三条边的长度分别是,,,记△ABC的周长为C△ABC.
①当x=2时,请直接写出△ABC中最长边的长度;
②若x为整数,当C△ABC取得最大值时,请用秦九韶公式求出△ABC的面积.
20.(12分)综合与探究:
如图1,平面直角坐标系中,一次函数图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C,点P是直线AB上的一个动点.
(1)求直线BC的表达式与点C的坐标;
(2)如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
(3)试探究x轴上是否存在点M,使以A,B,M为顶点的三角形是等腰三角形.若存在,直接写出点M的坐标;若不存在,说明理由.
2024-2025学年广东省深圳市盐田区八年级(上)期中数学试卷
参考答案
一、单选题:(每小题只有一个正确选项,每小题3分,共计24分)
1.(3分)实数,,,2π,,|﹣3|,0.313113111…(每两个3之间依次多一个1)中,无理数的个数是( )
A.2个 B.3个 C.4个 D.5个
选:C.
2.(3分)如图,已知OA=OB,点A到数轴的距离为1,则数轴上B点所表示的数为( )
A.﹣ B.﹣ C. D.
选:A.
3.(3分)下列运算正确的是( )
A. B. C. D.
选:D.
4.(3分)如图,一棵大树被台风刮断,若树在离地面3m处折断,树顶端落在离树底部4m处,则树折断之前高( )
A.5m B.7m C.8m D.10m
选:C.
5.(3分)对于函数y=﹣2x+3的图象,下列结论错误的是( )
A.图象必经过点(1,1)
B.图象经过第一、二、四象限
C.与x轴的交点为(0,3)
D.若两点A(1,y1),B(3,y2)在该函数图象上,则y1>y2
选:C.
6.(3分)将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内现用一个注水管沿大容器内壁匀速注水,如图,则大圆柱形容器水面的高度h(cm)与注水时间t(min)的函数图象大致( )
A. B.
C. D.
选:C.
7.(3分)如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A. B.
C. D.
选:C.
8.(3分)如图,在长方形纸片ABCD中,AB=8cm,AD=4cm.把纸片沿对角线AC折叠,点B落在点E处,AE交DC于点F,则重叠部分△ACF的面积为( )
A.5cm2 B.10cm2 C.15cm2 D.20cm2
选:B.
二、填空题:(本大题共5小题,每小题3分,共计15分)
9.(3分)﹣3是 ﹣27 的立方根.
10.(3分)直线y=2x+2沿y轴向下平移6个单位后与x轴的交点坐标是 (2,0) .
11.(3分)埃及胡夫金字塔是古代世界建筑奇迹之一,其底面是正方形,侧面是全等的等腰三角形,底面正方形的边长与侧面等腰三角形底边上的高的比值是,它介于整数n和n+1之间,则n的值是 1 .
12.(3分)△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D.则BD长为 .
13.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=12,BC=16,点D、E分别是AB,BC上动点,且AD=BE,连接CD,AE,则CD+AE的最小值是 4 .
三、解答题:(本题共7小题,其中第14题5分,第15题7分,第16题8分,第17题8分,第18题9分,第19题12分,第20题12分,共61分)
14.(5分)计算:.
【解答】解:原式=
=
=.
15.(7分)已知:a、b、c满足+|c﹣3|=0.
(1)求a、b、c的值;
(2)试问以a、b、c为边能否构成三角形?若能构成三角形,请判断三角形的形状;若不能构成三角形,请说明理由.
【解答】解:(1)∵,
∴,b﹣6=0,,
∴,b=6,;
(2)∵1<2<9,
∴,即,
∴,
∴以a、b、c为边能构成三角形,
∵,b=6,
∴a2+c2=b2,
∴三角形的形状是等腰直角三角形.
16.(8分)如图所示的正方形网格中,每个小正方形的边长为1,△ABC为格点三角形(顶点是网格线的交点的三角形),点B的坐标是(﹣2,0).
(1)点A的坐标是 (﹣5,4) ,点C的坐标是 (﹣1,2) ;
(2)请作出△ABC关于x轴对称的△A′B′C′;(点A与点A′对应,点B与点B′对应,点C与点C′对应)
(3)y轴上存在点P,使得PA+PC的值最小.则PA+PC的最小值是 .
【解答】解:(1)由图可得,A(﹣5,4),C(﹣1,2).
故答案为:(﹣5,4);(﹣1,2).
(2)如图,△A′B′C′即为所求.
(3)取点C关于y轴的对称点C'',连接AC''交y轴于点P,连接CP,
此时PA+PC=PA+PC''=AC'',为最小值,
由勾股定理得,AC''==,
∴PA+PC的最小值是.
故答案为:.
17.(8分)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地.送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺),将它往前推进两步(EB=10尺,BE⊥OA于E),此时踏板升高离地五尺(EC=BD=5尺),求秋千绳索(OA或OB)的长度.
【解答】解:设OA=OB=x尺,
∵EC=BD=5尺,AC=1尺,
∴EA=EC﹣AC=5﹣1=4(尺),OE=OA﹣AE=(x﹣4)尺,
在Rt△OEB中,OE=(x﹣4)尺,OB=x尺,EB=10尺,
根据勾股定理得:x2=(x﹣4)2+102,
整理得:8x=116,
即2x=29,
解得:x=14.5,
则秋千绳索的长度为14.5尺.
18.(9分)我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过8吨时,水价为每吨1.5元,超过8吨时,超过的部分按每吨2.2元收费.该市某户居民10月份用水x吨,应交水费y元.
(1)若0<x≤8,请写出y与x的函数关系式.
(2)若x>8,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费23元,那么这个月该户用了多少吨水?
【解答】解:(1)根据题意可知:
当0<x≤8时,y=1.5x;
(2)根据题意可知:
当x>8时,y=1.5×8+2.2×(x﹣8)=2.2x﹣5.6;
(3)∵当0<x≤8时,y=1.5x,
y的最大值为1.5×8=12(元),12<23,
∴该户当月用水超过8吨.
令y=2.2x﹣5.6中y=23,则23=2.2x﹣5.6,
解得:x=13.
答:这个月该户用了13吨水.
19.(12分)问题情境:在学习了《勾股定理》和《实数》后,某班同学们以“已知三角形三边的长度,求三角形面积”为主题开展了数学活动,同学们想到借助曾经阅读的数学资料进行探究:
材料1.古希腊的几何学家海伦(Heron,约公元50年),在他的著作《度量》一书中,给出了求其面积的海伦公式(其中a,b,c为三角形的三边长,,S为三角形的面积).
材料2.我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式:S=,其中三角形边长分别为a,b,c,三角形的面积为S.
(1)利用材料1解决下面的问题:当,b=3,时,求这个三角形的面积?
(2)利用材料2解决下面的问题:已知△ABC三条边的长度分别是,,,记△ABC的周长为C△ABC.
①当x=2时,请直接写出△ABC中最长边的长度;
②若x为整数,当C△ABC取得最大值时,请用秦九韶公式求出△ABC的面积.
【解答】解:(1)当,b=3,时,==,
∴p﹣a=﹣=,
p﹣b=﹣3=,
p﹣c=﹣2=,
∴p(p﹣a)(p﹣b)(p﹣c)=×××=×=9×1=9,
∴==3,
∴三角形的面积为3;
(2)①当x=2时,
=,=3,=4﹣()2=4﹣2=2,
故△ABC中最长边的长度为3;
②∵x+1≥0,4﹣x≥0,
∴﹣1≤x≤4.
∵4﹣()2=4﹣(4﹣x)=x,三角形的边为正值,
∴x>0,
∴0<x≤4.
∴=5﹣x,4﹣()2=4﹣(4﹣x)=x,
∴C△ABC=++
=+5﹣x+x
=+5,
∵C△ABC=+5(﹣1≤x≤4),且x为整数,
当x=4时,三边为,1,4,
∵+1<4,
∴不合题意舍去,
当x=3时,三边为2,2,3,
∴C△ABC=2+2+3=7,
∴S△ABC=
=
=
=.
∴△ABC的面积为.
20.(12分)综合与探究:
如图1,平面直角坐标系中,一次函数图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C,点P是直线AB上的一个动点.
(1)求直线BC的表达式与点C的坐标;
(2)如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
(3)试探究x轴上是否存在点M,使以A,B,M为顶点的三角形是等腰三角形.若存在,直接写出点M的坐标;若不存在,说明理由.
【解答】解:(1)令y=0,则x+3=0,
∴x=﹣6,
∴A(﹣6,0),
令x=0,则y=3,
∴B(0,3),
∵一次函数y=﹣x+b的图象经过点B,
∴b=3,
∴y=﹣x+3,
令y=0,则x=3,
∴C(3,0);
(2)存在,理由如下:
设P(t,t+3),则Q(t,﹣t+3),
∴PQ=|t|,
∵B(0,3),C(3,0),
∴BC=3,
∵PQ=BC,
∴|t|=3,
∴t=2或t=﹣2,
∴P(2,+3)或P(﹣2,﹣+3);
(3)存在,理由如下:
∵A(﹣6,0),B(0,3),
∴AB=3,
①当以A为等腰三角形的顶点时,
AB=AM=3,
∴M(﹣6+3,0)或(﹣6﹣3,0);
②当以B为等腰三角形的顶点时,
AB=BM,
∴M点与A点关于y轴对称,
∴M(6,0);
③当以M为等腰三角形的顶点时,
MA=MB,
设M(m,0),
∴(m+6)2=m2+9,
∴m=﹣,
∴M(﹣,0);
综上所述:M点的坐标为(﹣6+3,0)或(﹣6﹣3,0)或(6,0)或(﹣,0).
同课章节目录
