2024-2025学年新疆乌鲁木齐市沙依巴克区九年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年新疆乌鲁木齐市沙依巴克区九年级(上)期中数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 590.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 20:27:39 | ||
图片预览



文档简介
2024-2025学年新疆乌鲁木齐市沙依巴克区九年级(上)期中数学试卷
一、单选题(本大题共9小题,每题3分,满分27分.每题给出的四个选项中,只有一项是正确的,请将所选代号的字母填写在答题卷中相应的表格内)
1.(3分)若关于x的一元二次方程为3x2﹣5x+1=0,它的二次项系数和一次项系数分别为( )
A.3,5 B.3,1 C.3x2,﹣5x D.3,﹣5
2.(3分)下面的图形是以数学家名字命名的,其中是轴对称图形的是( )
A.斐波那契螺旋线 B.笛卡尔心形线
C.赵爽弦图 D.阿基米德曲线
3.(3分)一元二次方程x2﹣1=0的解为( )
A.x1=﹣1,x2=1 B.x=﹣1
C.x=0 D.x=1
4.(3分)平面直角坐标系内,点P(2,﹣3)关于原点对称点的坐标是( )
A.(3,﹣2) B.(2,3) C.(2,﹣3) D.(﹣2,3)
5.(3分)方程x2+x+6=0的根的情况是( )
A.有两个不等的实数根 B.有两个相等的实数根
C.无实数根 D.无法判断
6.(3分)如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )
A.20° B.25° C.30° D.35°
7.(3分)若点A(﹣3,y1),B(﹣2,y2),C(2,y3)都在二次函数y=x2﹣2x﹣3的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y3<y1<y2
8.(3分)科学兴趣小组的同学们,将自己收集的标本向本组的其他成员各赠送一件,全组共互赠了132件,设全组共有x名学生,则x满足的方程是( )
A. B.x(x+1)=132
C. D.x(x﹣1)=132
9.(3分)对称轴为直线x=1的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc>0,②b2<4ac,③4a+2b+c>0,④3a+c>0,⑤当x<﹣1时,y随x的增大而减小.其中结论正确为( )
A.①②④ B.①③⑤ C.①②③ D.①④⑤
二、填空题(本大题共5小题,每题3分,共15分,将答案直接写在答卷中相应各题的横线上)
10.(3分)方程x(x﹣1)=0的一个根是x=0,则另一个根是 .
11.(3分)二次函数y=(x﹣3)2+4的顶点坐标是 .
12.(3分)如图,将△ABC绕点A逆时针旋转到△ADE的位置,B、D、C在一条直线上.若∠B=70°,则∠EDC= °.
13.(3分)某段公路上汽车紧急刹车后前行的距离s(单位:m)关于行驶时间t(单位:s)的函数解析式是s=30t﹣5t2,遇到刹车时,汽车从刹车后到停下来前进了 m.
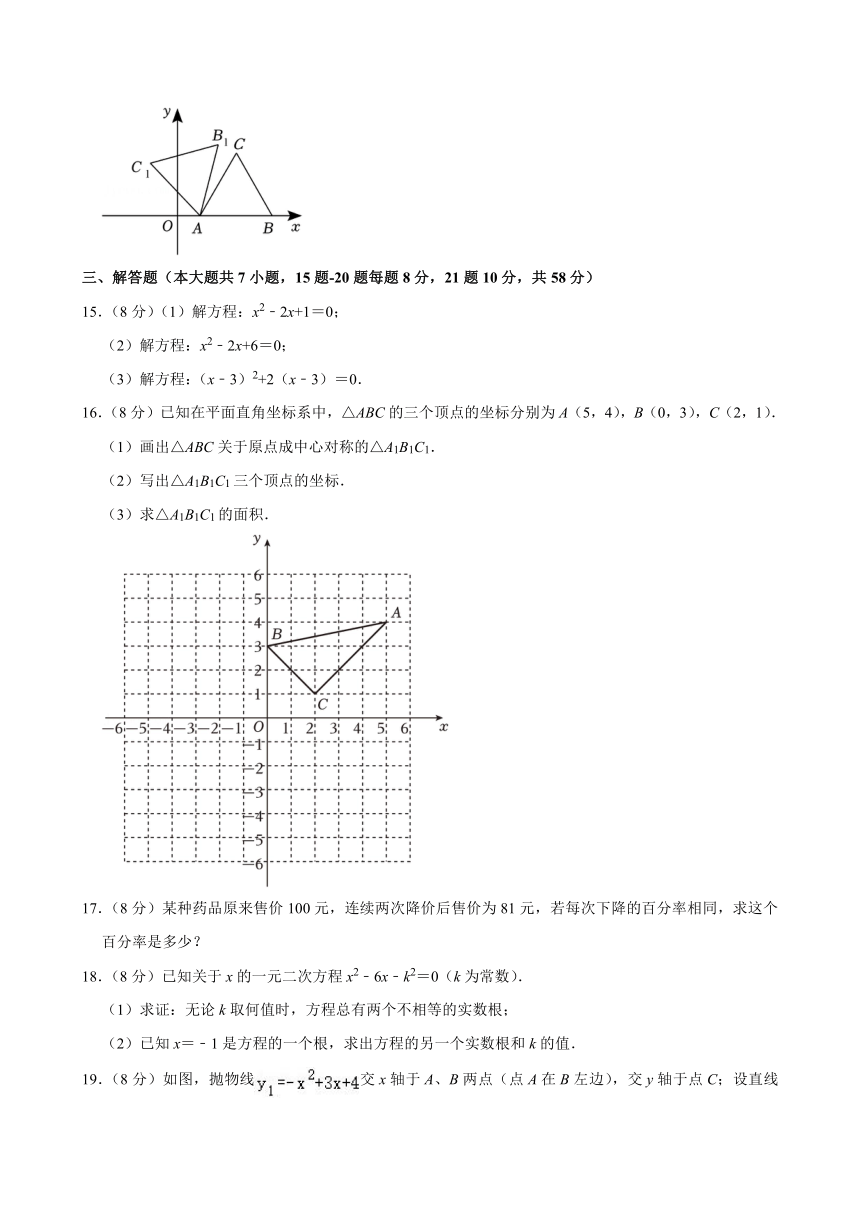
14.(3分)如图,点A(1,0),点B(5,0),线段AB绕点A逆时针旋转60°得到线段AC,连接BC,再把△ABC绕点A逆时针旋转75°得到△AB1C1,点C的对应点为点C1,则点C1的坐标是 .
三、解答题(本大题共7小题,15题-20题每题8分,21题10分,共58分)
15.(8分)(1)解方程:x2﹣2x+1=0;
(2)解方程:x2﹣2x+6=0;
(3)解方程:(x﹣3)2+2(x﹣3)=0.
16.(8分)已知在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
(1)画出△ABC关于原点成中心对称的△A1B1C1.
(2)写出△A1B1C1三个顶点的坐标.
(3)求△A1B1C1的面积.
17.(8分)某种药品原来售价100元,连续两次降价后售价为81元,若每次下降的百分率相同,求这个百分率是多少?
18.(8分)已知关于x的一元二次方程x2﹣6x﹣k2=0(k为常数).
(1)求证:无论k取何值时,方程总有两个不相等的实数根;
(2)已知x=﹣1是方程的一个根,求出方程的另一个实数根和k的值.
19.(8分)如图,抛物线交x轴于A、B两点(点A在B左边),交y轴于点C;设直线BC解析式为:y2=kx+b.
(1)求A、B两点的坐标;
(2)求直线BC的函数关系式;
(3)请直接写出y1<y2时的自变量x取值范围.
20.(8分)如图,四边形ABCD是正方形,△ADF绕着点A顺时针旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
21.(10分)如图抛物线y=ax2+bx+c经过点A(﹣1,0),点C(0,3),且OB=OC.
(1)求抛物线的解析式及其对称轴;
(2)点D、E是直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值.
(3)点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为3:5两部分,求点P的坐标.
2024-2025学年新疆乌鲁木齐市沙依巴克区九年级(上)期中数学试卷
参考答案
一、单选题(本大题共9小题,每题3分,满分27分.每题给出的四个选项中,只有一项是正确的,请将所选代号的字母填写在答题卷中相应的表格内)
1.(3分)若关于x的一元二次方程为3x2﹣5x+1=0,它的二次项系数和一次项系数分别为( )
A.3,5 B.3,1 C.3x2,﹣5x D.3,﹣5
选:D.
2.(3分)下面的图形是以数学家名字命名的,其中是轴对称图形的是( )
A.斐波那契螺旋线 B.笛卡尔心形线
C.赵爽弦图 D.阿基米德曲线
选:B.
3.(3分)一元二次方程x2﹣1=0的解为( )
A.x1=﹣1,x2=1 B.x=﹣1
C.x=0 D.x=1
选:A.
4.(3分)平面直角坐标系内,点P(2,﹣3)关于原点对称点的坐标是( )
A.(3,﹣2) B.(2,3) C.(2,﹣3) D.(﹣2,3)
选:D.
5.(3分)方程x2+x+6=0的根的情况是( )
A.有两个不等的实数根 B.有两个相等的实数根
C.无实数根 D.无法判断
选:C.
6.(3分)如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )
A.20° B.25° C.30° D.35°
选:B.
7.(3分)若点A(﹣3,y1),B(﹣2,y2),C(2,y3)都在二次函数y=x2﹣2x﹣3的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y3<y1<y2
选:C.
8.(3分)科学兴趣小组的同学们,将自己收集的标本向本组的其他成员各赠送一件,全组共互赠了132件,设全组共有x名学生,则x满足的方程是( )
A. B.x(x+1)=132
C. D.x(x﹣1)=132
选:D.
9.(3分)对称轴为直线x=1的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc>0,②b2<4ac,③4a+2b+c>0,④3a+c>0,⑤当x<﹣1时,y随x的增大而减小.其中结论正确为( )
A.①②④ B.①③⑤ C.①②③ D.①④⑤
选:D.
二、填空题(本大题共5小题,每题3分,共15分,将答案直接写在答卷中相应各题的横线上)
10.(3分)方程x(x﹣1)=0的一个根是x=0,则另一个根是 1 .
【解答】解:∵x(x﹣1)=0,
∴x=0或x﹣1=0,
∴x1=0,x2=1,
∴另一个根是1.
故答案为:1.
11.(3分)二次函数y=(x﹣3)2+4的顶点坐标是 (3,4) .
【解答】解:二次函数y=(x﹣3)2+4的顶点坐标是:(3,4).
故答案为:(3,4).
12.(3分)如图,将△ABC绕点A逆时针旋转到△ADE的位置,B、D、C在一条直线上.若∠B=70°,则∠EDC= 40 °.
【解答】解:∵将△ABC绕点A逆时针旋转到△ADE的位置,
∴AB=AD,∠B=∠ADE=70°,
∴∠B=∠ADB=∠ADE=70°,
∴∠EDC=180°﹣∠ADE﹣∠ADB
=180°﹣70°﹣70°
=40°,
故答案为:40.
13.(3分)某段公路上汽车紧急刹车后前行的距离s(单位:m)关于行驶时间t(单位:s)的函数解析式是s=30t﹣5t2,遇到刹车时,汽车从刹车后到停下来前进了 45 m.
【解答】解:∵s=﹣5t2+30t=﹣5(t﹣3)2+45,
∴汽车刹车后到停下来前进了45m,
故答案为:45.
14.(3分)如图,点A(1,0),点B(5,0),线段AB绕点A逆时针旋转60°得到线段AC,连接BC,再把△ABC绕点A逆时针旋转75°得到△AB1C1,点C的对应点为点C1,则点C1的坐标是 .
【解答】解:如图,过点C1D⊥x轴于点D,
∵线段AB绕点A逆时针旋转60°得到线段AC,连接BC,
∴△ABC是等边三角形,
∴∠BAC=60°,
∵把△ABC绕点A逆时针旋转75°得到△AB1C1,
∴∠CAC1=75°,
∴∠C1AD=45°,
∴△AC1D是等腰直角三角形,
∵点A(1,0),点B(5,0),
∴AB=4,
∵AC1=AC=AB=4,
∴,
∴,
∴,
故答案为:.
三、解答题(本大题共7小题,15题-20题每题8分,21题10分,共58分)
15.(8分)(1)解方程:x2﹣2x+1=0;
(2)解方程:x2﹣2x+6=0;
(3)解方程:(x﹣3)2+2(x﹣3)=0.
【解答】解:(1)x2﹣2x+1=0,
(x﹣1)2=0,
x1=x2=1;
(2)x2﹣2x+6=0;
x2﹣2x=﹣6,
x2﹣2x+1=﹣5,
(x﹣1)2=﹣5,
方程无解;
(3)(x﹣3)2+2(x﹣3)=0.
(x﹣3)(x﹣1)=0,
x1=3,x2=1.
16.(8分)已知在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
(1)画出△ABC关于原点成中心对称的△A1B1C1.
(2)写出△A1B1C1三个顶点的坐标.
(3)求△A1B1C1的面积.
【解答】解:(1)如图,△A1B1C1即为所求;
(2)由图可知,A1(﹣5,﹣4),B1(0,﹣3),C1(﹣2,﹣1);
(3)△A1B1C1的面积=3×5﹣×1×5﹣×2×2﹣×3×3=6.
17.(8分)某种药品原来售价100元,连续两次降价后售价为81元,若每次下降的百分率相同,求这个百分率是多少?
【解答】解:设每次下降的百分率为x,
100(1﹣x)2=81,
解得,x1=0.1,x2=1.9(舍去),
即这个百分率是10%.
18.(8分)已知关于x的一元二次方程x2﹣6x﹣k2=0(k为常数).
(1)求证:无论k取何值时,方程总有两个不相等的实数根;
(2)已知x=﹣1是方程的一个根,求出方程的另一个实数根和k的值.
【解答】(1)证明:Δ=(﹣6)2﹣4×1×(﹣k2)=4k2+36.
∵k2≥0,
∴4k2+36>0,
∴Δ>0,
∴方程有两个不相等的实数根;
(2)∵x1+x2=,x1 x2=,
又∵x=﹣1是方程的一个根,
∴﹣1+x2=6,
解得x2=7,
﹣1×7=﹣k2,
解得k=.
19.(8分)如图,抛物线交x轴于A、B两点(点A在B左边),交y轴于点C;设直线BC解析式为:y2=kx+b.
(1)求A、B两点的坐标;
(2)求直线BC的函数关系式;
(3)请直接写出y1<y2时的自变量x取值范围.
【解答】解:(1)在中,当时,解得x=﹣1或x=4,
∴A(﹣1,0),B(4,0);
(2)当x=0时,y1=4,
∴C(0,4),
∴,
∴,
∴直线BC的函数关系式y2=﹣x+4;
(3)由函数图象可知,当二次函数图象在一次函数图象下方时自变量的取值范围为x<0或x>4,
∴当y1<y2时,x<0或x>4.
20.(8分)如图,四边形ABCD是正方形,△ADF绕着点A顺时针旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
【解答】解:(1)∵△ADF按顺时针方向旋转90°后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转90°后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
21.(10分)如图抛物线y=ax2+bx+c经过点A(﹣1,0),点C(0,3),且OB=OC.
(1)求抛物线的解析式及其对称轴;
(2)点D、E是直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值.
(3)点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为3:5两部分,求点P的坐标.
【解答】解:(1)∵OB=OC,∴点B(3,0),
则抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3)=ax2﹣2ax﹣3a,
故﹣3a=3,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+3…①,
函数的对称轴为:x=1;
(2)四边形ACDE的周长=AC+DE+CD+AE,其中AC=、DE=1是常数,
故CD+AE最小时,周长最小,
取点C关于直线x=1对称点C′(2,3),则CD=C′D,
取点A′(﹣1,1),则A′D=AE,
故:CD+AE=A′D+DC′,则当A′、D、C′三点共线时,CD+AE=A′D+DC′最小,周长也最小,
四边形ACDE的周长的最小值=AC+DE+CD+AE=+A′D+DC′=+A′C′=+;
(3)如图,设直线CP交x轴于点E,
直线CP把四边形CBPA的面积分为3:5两部分,
又∵S△PCB:S△PCA=EB×(yC﹣yP):AE×(yC﹣yP)=BE:AE,
则BE:AE=3:5或5:3,
则AE=或,
即:点E的坐标为(,0)或(,0),
将点E的坐标代入直线CP的表达式:y=kx+3,
解得:k=﹣6或﹣2,
故直线CP的表达式为:y=﹣2x+3或y=﹣6x+3…②
联立①②并解得:x=4或8(不合题意值已舍去),
故点P的坐标为(4,﹣5)或(8,﹣45).
一、单选题(本大题共9小题,每题3分,满分27分.每题给出的四个选项中,只有一项是正确的,请将所选代号的字母填写在答题卷中相应的表格内)
1.(3分)若关于x的一元二次方程为3x2﹣5x+1=0,它的二次项系数和一次项系数分别为( )
A.3,5 B.3,1 C.3x2,﹣5x D.3,﹣5
2.(3分)下面的图形是以数学家名字命名的,其中是轴对称图形的是( )
A.斐波那契螺旋线 B.笛卡尔心形线
C.赵爽弦图 D.阿基米德曲线
3.(3分)一元二次方程x2﹣1=0的解为( )
A.x1=﹣1,x2=1 B.x=﹣1
C.x=0 D.x=1
4.(3分)平面直角坐标系内,点P(2,﹣3)关于原点对称点的坐标是( )
A.(3,﹣2) B.(2,3) C.(2,﹣3) D.(﹣2,3)
5.(3分)方程x2+x+6=0的根的情况是( )
A.有两个不等的实数根 B.有两个相等的实数根
C.无实数根 D.无法判断
6.(3分)如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )
A.20° B.25° C.30° D.35°
7.(3分)若点A(﹣3,y1),B(﹣2,y2),C(2,y3)都在二次函数y=x2﹣2x﹣3的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y3<y1<y2
8.(3分)科学兴趣小组的同学们,将自己收集的标本向本组的其他成员各赠送一件,全组共互赠了132件,设全组共有x名学生,则x满足的方程是( )
A. B.x(x+1)=132
C. D.x(x﹣1)=132
9.(3分)对称轴为直线x=1的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc>0,②b2<4ac,③4a+2b+c>0,④3a+c>0,⑤当x<﹣1时,y随x的增大而减小.其中结论正确为( )
A.①②④ B.①③⑤ C.①②③ D.①④⑤
二、填空题(本大题共5小题,每题3分,共15分,将答案直接写在答卷中相应各题的横线上)
10.(3分)方程x(x﹣1)=0的一个根是x=0,则另一个根是 .
11.(3分)二次函数y=(x﹣3)2+4的顶点坐标是 .
12.(3分)如图,将△ABC绕点A逆时针旋转到△ADE的位置,B、D、C在一条直线上.若∠B=70°,则∠EDC= °.
13.(3分)某段公路上汽车紧急刹车后前行的距离s(单位:m)关于行驶时间t(单位:s)的函数解析式是s=30t﹣5t2,遇到刹车时,汽车从刹车后到停下来前进了 m.
14.(3分)如图,点A(1,0),点B(5,0),线段AB绕点A逆时针旋转60°得到线段AC,连接BC,再把△ABC绕点A逆时针旋转75°得到△AB1C1,点C的对应点为点C1,则点C1的坐标是 .
三、解答题(本大题共7小题,15题-20题每题8分,21题10分,共58分)
15.(8分)(1)解方程:x2﹣2x+1=0;
(2)解方程:x2﹣2x+6=0;
(3)解方程:(x﹣3)2+2(x﹣3)=0.
16.(8分)已知在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
(1)画出△ABC关于原点成中心对称的△A1B1C1.
(2)写出△A1B1C1三个顶点的坐标.
(3)求△A1B1C1的面积.
17.(8分)某种药品原来售价100元,连续两次降价后售价为81元,若每次下降的百分率相同,求这个百分率是多少?
18.(8分)已知关于x的一元二次方程x2﹣6x﹣k2=0(k为常数).
(1)求证:无论k取何值时,方程总有两个不相等的实数根;
(2)已知x=﹣1是方程的一个根,求出方程的另一个实数根和k的值.
19.(8分)如图,抛物线交x轴于A、B两点(点A在B左边),交y轴于点C;设直线BC解析式为:y2=kx+b.
(1)求A、B两点的坐标;
(2)求直线BC的函数关系式;
(3)请直接写出y1<y2时的自变量x取值范围.
20.(8分)如图,四边形ABCD是正方形,△ADF绕着点A顺时针旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
21.(10分)如图抛物线y=ax2+bx+c经过点A(﹣1,0),点C(0,3),且OB=OC.
(1)求抛物线的解析式及其对称轴;
(2)点D、E是直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值.
(3)点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为3:5两部分,求点P的坐标.
2024-2025学年新疆乌鲁木齐市沙依巴克区九年级(上)期中数学试卷
参考答案
一、单选题(本大题共9小题,每题3分,满分27分.每题给出的四个选项中,只有一项是正确的,请将所选代号的字母填写在答题卷中相应的表格内)
1.(3分)若关于x的一元二次方程为3x2﹣5x+1=0,它的二次项系数和一次项系数分别为( )
A.3,5 B.3,1 C.3x2,﹣5x D.3,﹣5
选:D.
2.(3分)下面的图形是以数学家名字命名的,其中是轴对称图形的是( )
A.斐波那契螺旋线 B.笛卡尔心形线
C.赵爽弦图 D.阿基米德曲线
选:B.
3.(3分)一元二次方程x2﹣1=0的解为( )
A.x1=﹣1,x2=1 B.x=﹣1
C.x=0 D.x=1
选:A.
4.(3分)平面直角坐标系内,点P(2,﹣3)关于原点对称点的坐标是( )
A.(3,﹣2) B.(2,3) C.(2,﹣3) D.(﹣2,3)
选:D.
5.(3分)方程x2+x+6=0的根的情况是( )
A.有两个不等的实数根 B.有两个相等的实数根
C.无实数根 D.无法判断
选:C.
6.(3分)如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )
A.20° B.25° C.30° D.35°
选:B.
7.(3分)若点A(﹣3,y1),B(﹣2,y2),C(2,y3)都在二次函数y=x2﹣2x﹣3的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y3<y1<y2
选:C.
8.(3分)科学兴趣小组的同学们,将自己收集的标本向本组的其他成员各赠送一件,全组共互赠了132件,设全组共有x名学生,则x满足的方程是( )
A. B.x(x+1)=132
C. D.x(x﹣1)=132
选:D.
9.(3分)对称轴为直线x=1的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc>0,②b2<4ac,③4a+2b+c>0,④3a+c>0,⑤当x<﹣1时,y随x的增大而减小.其中结论正确为( )
A.①②④ B.①③⑤ C.①②③ D.①④⑤
选:D.
二、填空题(本大题共5小题,每题3分,共15分,将答案直接写在答卷中相应各题的横线上)
10.(3分)方程x(x﹣1)=0的一个根是x=0,则另一个根是 1 .
【解答】解:∵x(x﹣1)=0,
∴x=0或x﹣1=0,
∴x1=0,x2=1,
∴另一个根是1.
故答案为:1.
11.(3分)二次函数y=(x﹣3)2+4的顶点坐标是 (3,4) .
【解答】解:二次函数y=(x﹣3)2+4的顶点坐标是:(3,4).
故答案为:(3,4).
12.(3分)如图,将△ABC绕点A逆时针旋转到△ADE的位置,B、D、C在一条直线上.若∠B=70°,则∠EDC= 40 °.
【解答】解:∵将△ABC绕点A逆时针旋转到△ADE的位置,
∴AB=AD,∠B=∠ADE=70°,
∴∠B=∠ADB=∠ADE=70°,
∴∠EDC=180°﹣∠ADE﹣∠ADB
=180°﹣70°﹣70°
=40°,
故答案为:40.
13.(3分)某段公路上汽车紧急刹车后前行的距离s(单位:m)关于行驶时间t(单位:s)的函数解析式是s=30t﹣5t2,遇到刹车时,汽车从刹车后到停下来前进了 45 m.
【解答】解:∵s=﹣5t2+30t=﹣5(t﹣3)2+45,
∴汽车刹车后到停下来前进了45m,
故答案为:45.
14.(3分)如图,点A(1,0),点B(5,0),线段AB绕点A逆时针旋转60°得到线段AC,连接BC,再把△ABC绕点A逆时针旋转75°得到△AB1C1,点C的对应点为点C1,则点C1的坐标是 .
【解答】解:如图,过点C1D⊥x轴于点D,
∵线段AB绕点A逆时针旋转60°得到线段AC,连接BC,
∴△ABC是等边三角形,
∴∠BAC=60°,
∵把△ABC绕点A逆时针旋转75°得到△AB1C1,
∴∠CAC1=75°,
∴∠C1AD=45°,
∴△AC1D是等腰直角三角形,
∵点A(1,0),点B(5,0),
∴AB=4,
∵AC1=AC=AB=4,
∴,
∴,
∴,
故答案为:.
三、解答题(本大题共7小题,15题-20题每题8分,21题10分,共58分)
15.(8分)(1)解方程:x2﹣2x+1=0;
(2)解方程:x2﹣2x+6=0;
(3)解方程:(x﹣3)2+2(x﹣3)=0.
【解答】解:(1)x2﹣2x+1=0,
(x﹣1)2=0,
x1=x2=1;
(2)x2﹣2x+6=0;
x2﹣2x=﹣6,
x2﹣2x+1=﹣5,
(x﹣1)2=﹣5,
方程无解;
(3)(x﹣3)2+2(x﹣3)=0.
(x﹣3)(x﹣1)=0,
x1=3,x2=1.
16.(8分)已知在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
(1)画出△ABC关于原点成中心对称的△A1B1C1.
(2)写出△A1B1C1三个顶点的坐标.
(3)求△A1B1C1的面积.
【解答】解:(1)如图,△A1B1C1即为所求;
(2)由图可知,A1(﹣5,﹣4),B1(0,﹣3),C1(﹣2,﹣1);
(3)△A1B1C1的面积=3×5﹣×1×5﹣×2×2﹣×3×3=6.
17.(8分)某种药品原来售价100元,连续两次降价后售价为81元,若每次下降的百分率相同,求这个百分率是多少?
【解答】解:设每次下降的百分率为x,
100(1﹣x)2=81,
解得,x1=0.1,x2=1.9(舍去),
即这个百分率是10%.
18.(8分)已知关于x的一元二次方程x2﹣6x﹣k2=0(k为常数).
(1)求证:无论k取何值时,方程总有两个不相等的实数根;
(2)已知x=﹣1是方程的一个根,求出方程的另一个实数根和k的值.
【解答】(1)证明:Δ=(﹣6)2﹣4×1×(﹣k2)=4k2+36.
∵k2≥0,
∴4k2+36>0,
∴Δ>0,
∴方程有两个不相等的实数根;
(2)∵x1+x2=,x1 x2=,
又∵x=﹣1是方程的一个根,
∴﹣1+x2=6,
解得x2=7,
﹣1×7=﹣k2,
解得k=.
19.(8分)如图,抛物线交x轴于A、B两点(点A在B左边),交y轴于点C;设直线BC解析式为:y2=kx+b.
(1)求A、B两点的坐标;
(2)求直线BC的函数关系式;
(3)请直接写出y1<y2时的自变量x取值范围.
【解答】解:(1)在中,当时,解得x=﹣1或x=4,
∴A(﹣1,0),B(4,0);
(2)当x=0时,y1=4,
∴C(0,4),
∴,
∴,
∴直线BC的函数关系式y2=﹣x+4;
(3)由函数图象可知,当二次函数图象在一次函数图象下方时自变量的取值范围为x<0或x>4,
∴当y1<y2时,x<0或x>4.
20.(8分)如图,四边形ABCD是正方形,△ADF绕着点A顺时针旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
【解答】解:(1)∵△ADF按顺时针方向旋转90°后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转90°后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
21.(10分)如图抛物线y=ax2+bx+c经过点A(﹣1,0),点C(0,3),且OB=OC.
(1)求抛物线的解析式及其对称轴;
(2)点D、E是直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值.
(3)点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为3:5两部分,求点P的坐标.
【解答】解:(1)∵OB=OC,∴点B(3,0),
则抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3)=ax2﹣2ax﹣3a,
故﹣3a=3,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+3…①,
函数的对称轴为:x=1;
(2)四边形ACDE的周长=AC+DE+CD+AE,其中AC=、DE=1是常数,
故CD+AE最小时,周长最小,
取点C关于直线x=1对称点C′(2,3),则CD=C′D,
取点A′(﹣1,1),则A′D=AE,
故:CD+AE=A′D+DC′,则当A′、D、C′三点共线时,CD+AE=A′D+DC′最小,周长也最小,
四边形ACDE的周长的最小值=AC+DE+CD+AE=+A′D+DC′=+A′C′=+;
(3)如图,设直线CP交x轴于点E,
直线CP把四边形CBPA的面积分为3:5两部分,
又∵S△PCB:S△PCA=EB×(yC﹣yP):AE×(yC﹣yP)=BE:AE,
则BE:AE=3:5或5:3,
则AE=或,
即:点E的坐标为(,0)或(,0),
将点E的坐标代入直线CP的表达式:y=kx+3,
解得:k=﹣6或﹣2,
故直线CP的表达式为:y=﹣2x+3或y=﹣6x+3…②
联立①②并解得:x=4或8(不合题意值已舍去),
故点P的坐标为(4,﹣5)或(8,﹣45).
同课章节目录
