浙江省丽水市文元教育集团2024-2025学年九年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 浙江省丽水市文元教育集团2024-2025学年九年级(上)期中数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 669.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 18:07:21 | ||
图片预览



文档简介
2024-2025学年浙江省丽水市文元教育集团九年级(上)期中数学试卷
一、选择题(本题有10小题,每小题3分,共30分)
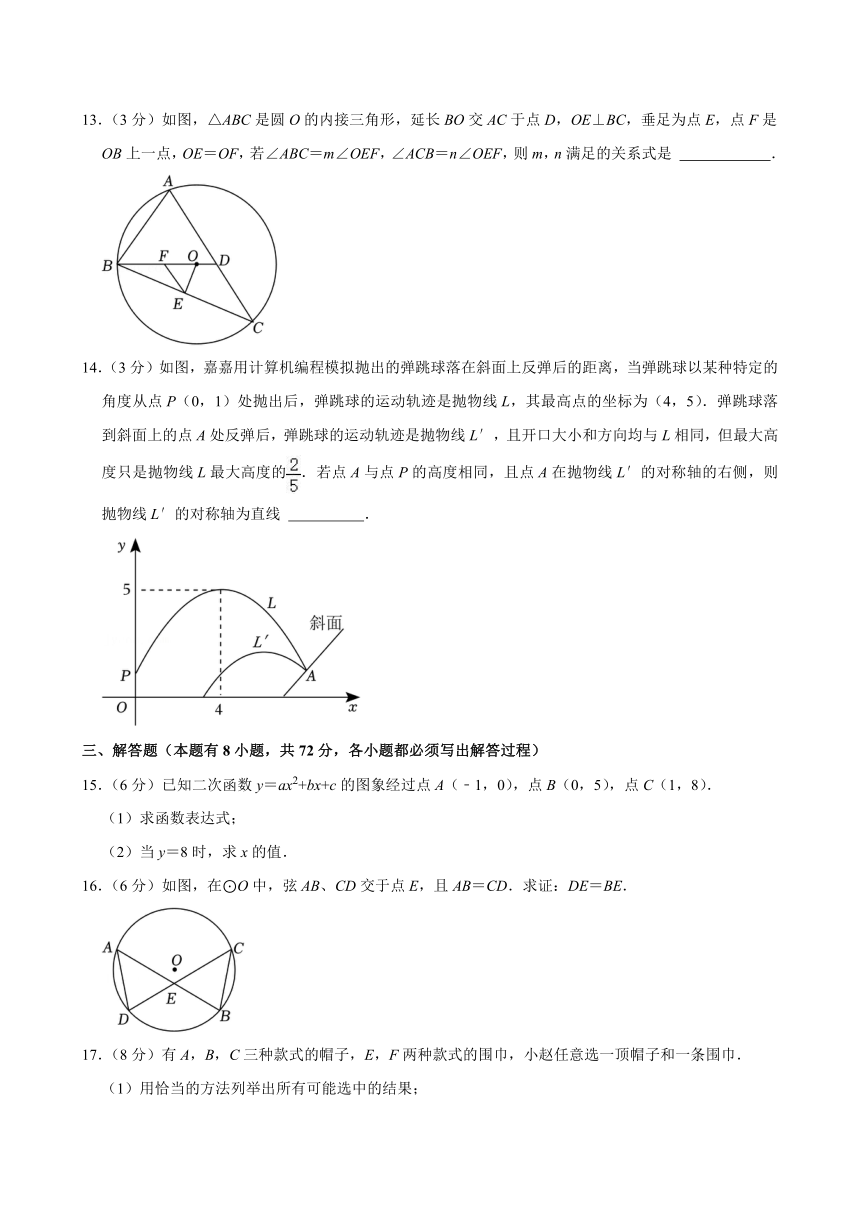
1.(3分)⊙O的半径为2cm,点P到圆心O的距离为,那么点A与⊙O的位置关系是( )
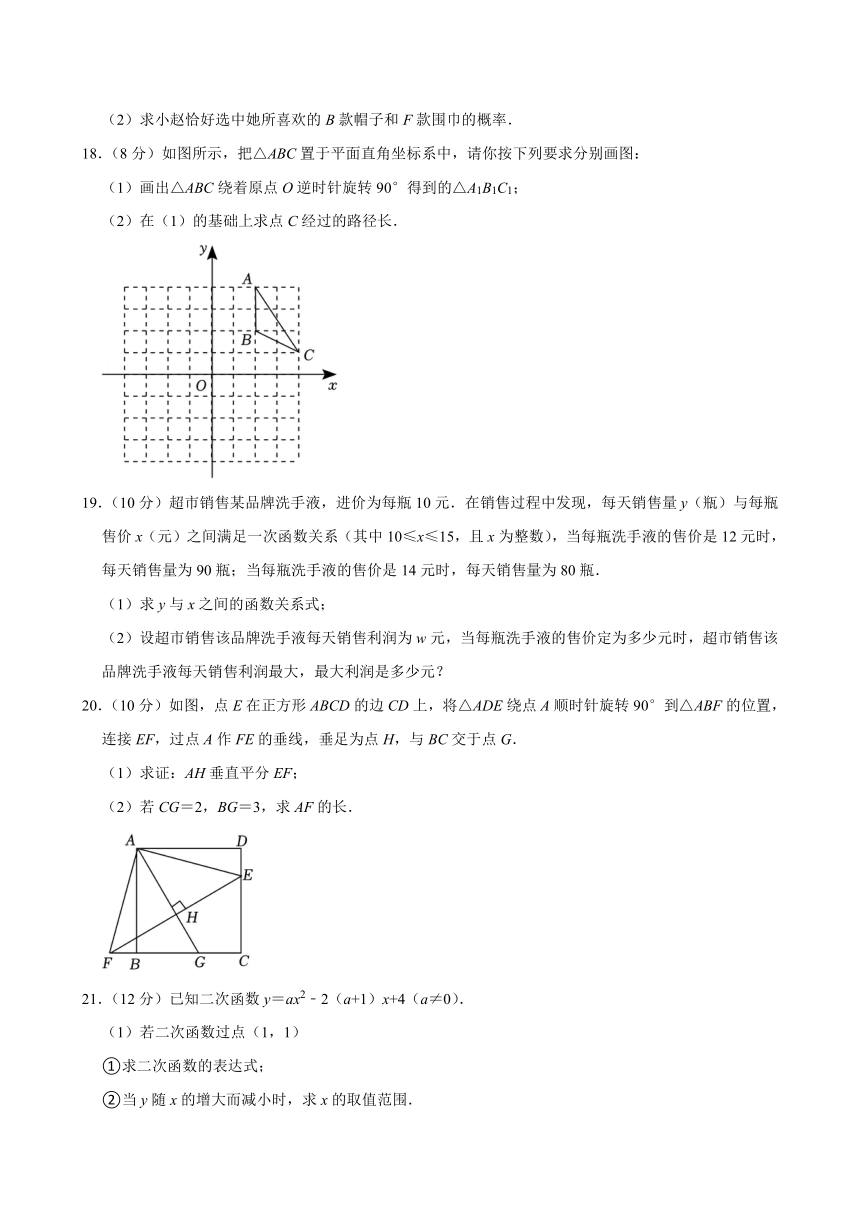
A.点P在圆内 B.点P在圆上 C.点P在圆外 D.点P在圆心
2.(3分)二次函数y=x2+1图象的顶点坐标是( )
A.(0,1) B.(﹣1,0) C.(0,﹣1) D.(1,0)
3.(3分)如图,该硬币边缘镌刻的正九边形每个内角的度数是( )
A.120° B.135° C.140° D.144°
4.(3分)如图,点A的坐标为(1,3),O为坐标原点,将OA绕点A按逆时针方向旋转90°得到AO′,则点O′的坐标是( )
A.(4,﹣1) B.(﹣1,4) C.(4,2) D.(2,﹣4)
5.(3分)如图,在⊙O的内接四边形ABCD中,E为直径AB延长线上的一点,若∠D=120°,∠BCE=20°,则∠E的度数为( )
A.30° B.35° C.40° D.45°
6.(3分)已知点A(1,y1),B(2,y2)在抛物线y=﹣(x+1)2+2上,则下列结论正确的是( )
A.y1>y2>2 B.y2>y1>2 C.2>y1>y2 D.2>y2>y1
7.(3分)如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π B.3π C.2π D.2π
8.(3分)如图,点P是正六边形ABCDEF内一点,AB=4,当∠APB=90°时,连接PD,则线段PD的最小值是( )
A. B. C.6 D.
二、填空题(本题有6小题,每小题3分,共18分)
9.(3分)在⊙O中,弦AB=3,圆心角∠A0B=60°,则⊙O的半径为 .
10.(3分)把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为 .
11.(3分)某鱼塘养了1000条草鱼、500条鲤鱼、若干条鲫鱼,鱼塘主通过多次捕捞试验发现,捕捞到鲫鱼的频率稳定在0.25左右.若鱼塘主随机在鱼塘里捕捞一条鱼,捕捞到草鱼的概率约为 .
12.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕点C顺时针旋转得到△A1B1C(点A与A1点B与B1对应).当点A,B1,A1在同一直线上时,AB1的长为 .
13.(3分)如图,△ABC是圆O的内接三角形,延长BO交AC于点D,OE⊥BC,垂足为点E,点F是OB上一点,OE=OF,若∠ABC=m∠OEF,∠ACB=n∠OEF,则m,n满足的关系式是 .
14.(3分)如图,嘉嘉用计算机编程模拟抛出的弹跳球落在斜面上反弹后的距离,当弹跳球以某种特定的角度从点P(0,1)处抛出后,弹跳球的运动轨迹是抛物线L,其最高点的坐标为(4,5).弹跳球落到斜面上的点A处反弹后,弹跳球的运动轨迹是抛物线L′,且开口大小和方向均与L相同,但最大高度只是抛物线L最大高度的.若点A与点P的高度相同,且点A在抛物线L′的对称轴的右侧,则抛物线L′的对称轴为直线 .
三、解答题(本题有8小题,共72分,各小题都必须写出解答过程)
15.(6分)已知二次函数y=ax2+bx+c的图象经过点A(﹣1,0),点B(0,5),点C(1,8).
(1)求函数表达式;
(2)当y=8时,求x的值.
16.(6分)如图,在⊙O中,弦AB、CD交于点E,且AB=CD.求证:DE=BE.
17.(8分)有A,B,C三种款式的帽子,E,F两种款式的围巾,小赵任意选一顶帽子和一条围巾.
(1)用恰当的方法列举出所有可能选中的结果;
(2)求小赵恰好选中她所喜欢的B款帽子和F款围巾的概率.
18.(8分)如图所示,把△ABC置于平面直角坐标系中,请你按下列要求分别画图:
(1)画出△ABC绕着原点O逆时针旋转90°得到的△A1B1C1;
(2)在(1)的基础上求点C经过的路径长.
19.(10分)超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量y(瓶)与每瓶售价x(元)之间满足一次函数关系(其中10≤x≤15,且x为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.
(1)求y与x之间的函数关系式;
(2)设超市销售该品牌洗手液每天销售利润为w元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?
20.(10分)如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作FE的垂线,垂足为点H,与BC交于点G.
(1)求证:AH垂直平分EF;
(2)若CG=2,BG=3,求AF的长.
21.(12分)已知二次函数y=ax2﹣2(a+1)x+4(a≠0).
(1)若二次函数过点(1,1)
①求二次函数的表达式;
②当y随x的增大而减小时,求x的取值范围.
(2)若点和点在该二次函数图象上,求的值.
22.(12分)如图,四边形ABCD内接于⊙O,AD为直径,AB=BC,BH⊥AD于H,AH=2,BH=4.
(1)求⊙O的半径;
(2)求四边形ABCD的面积;
(3)E是线段BD上一点,BE=BC,连接CE并延长交⊙O于F,求CF的长.
2024-2025学年浙江省丽水市文元教育集团九年级(上)期中数学试卷
参考答案
一、选择题(本题有10小题,每小题3分,共30分)
1.(3分)⊙O的半径为2cm,点P到圆心O的距离为,那么点A与⊙O的位置关系是( )
A.点P在圆内 B.点P在圆上 C.点P在圆外 D.点P在圆心
选:A.
2.(3分)二次函数y=x2+1图象的顶点坐标是( )
A.(0,1) B.(﹣1,0) C.(0,﹣1) D.(1,0)
选:A.
3.(3分)如图,该硬币边缘镌刻的正九边形每个内角的度数是( )
A.120° B.135° C.140° D.144°
选:C.
4.(3分)如图,点A的坐标为(1,3),O为坐标原点,将OA绕点A按逆时针方向旋转90°得到AO′,则点O′的坐标是( )
A.(4,﹣1) B.(﹣1,4) C.(4,2) D.(2,﹣4)
选:C.
5.(3分)如图,在⊙O的内接四边形ABCD中,E为直径AB延长线上的一点,若∠D=120°,∠BCE=20°,则∠E的度数为( )
A.30° B.35° C.40° D.45°
选:C.
6.(3分)已知点A(1,y1),B(2,y2)在抛物线y=﹣(x+1)2+2上,则下列结论正确的是( )
A.y1>y2>2 B.y2>y1>2 C.2>y1>y2 D.2>y2>y1
选:C.
7.(3分)如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π B.3π C.2π D.2π
选:A.
8.(3分)如图,点P是正六边形ABCDEF内一点,AB=4,当∠APB=90°时,连接PD,则线段PD的最小值是( )
A. B. C.6 D.
选:B.
二、填空题(本题有6小题,每小题3分,共18分)
9.(3分)在⊙O中,弦AB=3,圆心角∠A0B=60°,则⊙O的半径为 3 .
10.(3分)把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为 y=﹣(x+1)2+3 .
11.(3分)某鱼塘养了1000条草鱼、500条鲤鱼、若干条鲫鱼,鱼塘主通过多次捕捞试验发现,捕捞到鲫鱼的频率稳定在0.25左右.若鱼塘主随机在鱼塘里捕捞一条鱼,捕捞到草鱼的概率约为 .
12.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕点C顺时针旋转得到△A1B1C(点A与A1点B与B1对应).当点A,B1,A1在同一直线上时,AB1的长为 .
13.(3分)如图,△ABC是圆O的内接三角形,延长BO交AC于点D,OE⊥BC,垂足为点E,点F是OB上一点,OE=OF,若∠ABC=m∠OEF,∠ACB=n∠OEF,则m,n满足的关系式是 m+n=2 .
14.(3分)如图,嘉嘉用计算机编程模拟抛出的弹跳球落在斜面上反弹后的距离,当弹跳球以某种特定的角度从点P(0,1)处抛出后,弹跳球的运动轨迹是抛物线L,其最高点的坐标为(4,5).弹跳球落到斜面上的点A处反弹后,弹跳球的运动轨迹是抛物线L′,且开口大小和方向均与L相同,但最大高度只是抛物线L最大高度的.若点A与点P的高度相同,且点A在抛物线L′的对称轴的右侧,则抛物线L′的对称轴为直线 x=6 .
三、解答题(本题有8小题,共72分,各小题都必须写出解答过程)
15.(6分)已知二次函数y=ax2+bx+c的图象经过点A(﹣1,0),点B(0,5),点C(1,8).
(1)求函数表达式;
(2)当y=8时,求x的值.
【解答】解:(1)根据题意得,
解得,
∴抛物线解析式为y=﹣x2+4x+5;
(2)当y=8时,﹣x2+4x+5=8,
解得x1=1,x2=3,
即x的值为1或3.
16.(6分)如图,在⊙O中,弦AB、CD交于点E,且AB=CD.求证:DE=BE.
【解答】证明:∵AB=CD,
∴,
∴,
即,
∴AD=CB,
在△AED和△CEB中,
,
∴△AED≌△CEB(AAS),
∴DE=BE.
17.(8分)有A,B,C三种款式的帽子,E,F两种款式的围巾,小赵任意选一顶帽子和一条围巾.
(1)用恰当的方法列举出所有可能选中的结果;
(2)求小赵恰好选中她所喜欢的B款帽子和F款围巾的概率.
【解答】解:(1)列表如下:
围巾帽子 E F
A (A,E) (A,F)
B (B,E) (B,F)
C (C,E) (C,F)
(2)由(1)得:共有6个等可能的结果,小赵恰好选中她所喜欢的B款帽子和F款围巾的结果有1个,
∴小赵恰好选中她所喜欢的B款帽子和F款围巾的概率为.
18.(8分)如图所示,把△ABC置于平面直角坐标系中,请你按下列要求分别画图:
(1)画出△ABC绕着原点O逆时针旋转90°得到的△A1B1C1;
(2)在(1)的基础上求点C经过的路径长.
【解答】解:(1)如图:△A1B1C1即为所求;
(2),
∴点C经过的路径长为.
19.(10分)超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量y(瓶)与每瓶售价x(元)之间满足一次函数关系(其中10≤x≤15,且x为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.
(1)求y与x之间的函数关系式;
(2)设超市销售该品牌洗手液每天销售利润为w元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?
【解答】解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),根据题意得:
,
解得:,
∴y与x之间的函数关系为y=﹣5x+150;
(2)根据题意得:w=(x﹣10)(﹣5x+150)=﹣5(x﹣20)2+500,
∵a=﹣5<0,
∴抛物线开口向下,w有最大值,
∴当x<20时,w随着x的增大而增大,
∵10≤x≤15且x为整数,
∴当x=15时,w有最大值,
即:w=﹣5×(15﹣20)2+500=375,
答:当每瓶洗手液的售价定为15元时,超市销售该品牌洗手液每天销售利润最大,最大利润为375元.
20.(10分)如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作FE的垂线,垂足为点H,与BC交于点G.
(1)求证:AH垂直平分EF;
(2)若CG=2,BG=3,求AF的长.
【解答】(1)证明:∵将△ADE绕点A顺时针旋转90°得到△ABF,
∴AF=AE,
∵AH⊥FE于点H,
∴FH=EH,
∴AH垂直平分EF.
(2)解:连接EG,
∵四边形ABCD是正方形,CG=2,BG=3,
∴∠ABC=∠C=∠D=90°,AB=AD=CD=BC=CG+BG=2+3=5,
由旋转得BF=DE,∠ABF=∠D=90°,
∴∠ABF+∠ABC=180°,
∴点F在CB的延长线上,
∵CG2+CE2=EG2,且CE=5﹣DE=5﹣BF,EG=FG=3+BF,
∴22+(5﹣BF)2=(3+BF)2,
解得BF=,
∴AF===,
∴AF的长是.
21.(12分)已知二次函数y=ax2﹣2(a+1)x+4(a≠0).
(1)若二次函数过点(1,1)
①求二次函数的表达式;
②当y随x的增大而减小时,求x的取值范围.
(2)若点和点在该二次函数图象上,求的值.
【解答】解:(1)①∵二次函数过点(1,1),
∴1=a﹣2(a+1)+4.
∴a=1.
∴二次函数的表达式为y=x2﹣4x+4.
②由①y=x2﹣4x+4=(x﹣2)2,
∴当x<2时,y随x的增大而减小.
∴当y随x的增大而减小时,x<2.
(2)∵y=ax2﹣2(a+1)x+4(a≠0),
∴抛物线对称轴为直线x=﹣=1+.
∵点P(,b)和点Q(+n,b)关于对称轴对称,
∴=1+.
∴n=2.
把P(,b)代入函数解析式得:a×﹣2(a+1)×+4=b,
解得b=2﹣.
∴(+b)2+n2=(+2﹣)2+22=8.
22.(12分)如图,四边形ABCD内接于⊙O,AD为直径,AB=BC,BH⊥AD于H,AH=2,BH=4.
(1)求⊙O的半径;
(2)求四边形ABCD的面积;
(3)E是线段BD上一点,BE=BC,连接CE并延长交⊙O于F,求CF的长.
【解答】解:(1)如图,连接OB,设⊙O半径为r,
在Rt△BOH中,OH=r﹣2,OB=r,BH=4,由勾股定理得:
r2=42+(r﹣2)2,
解得:r=5,
∴⊙O的半径为5;
(2)如图,过B作BG⊥DC,交DC延长线于点G,
∵AB=BC,
∴∠ADB=∠BDC,
∴BD是∠ADC的平分线,
∴BH=BG=4,DH=DG=10﹣2=8,
∵AB=BC,BH=BG,
∴△ABH≌△BCG(HL),
∴AH=CG =2,
∴CD=8﹣2=6,
S四边形ABCD=S△ABD+S△BCD=+=32.
(3)如图,连接DF,过C作CG⊥BD于点G,则∠BGC=90°,
由(2)得:OH=3,BH=4,
∴AH=2,
∴,同理得:,
∵AB=BC,BC=BE,
∴,
∴,
∵∠BGC=∠AMO=90°,∠CBG=∠MAO,
∴△BGC∽△AMO,
∴,
∴,即,
∴,
由勾股定理得:,
∴,
在Rt△CGE中,由勾股定理得:,
∵∠CBE=∠EFD,∠BCE=∠FDE,
∴△BCE∽△FDE,
∴,
∴,则,
∵BE=BC,
∴∠BCE=∠BEC=∠FED,
∴∠FED=∠FDE,
∴,
∴.
一、选择题(本题有10小题,每小题3分,共30分)
1.(3分)⊙O的半径为2cm,点P到圆心O的距离为,那么点A与⊙O的位置关系是( )
A.点P在圆内 B.点P在圆上 C.点P在圆外 D.点P在圆心
2.(3分)二次函数y=x2+1图象的顶点坐标是( )
A.(0,1) B.(﹣1,0) C.(0,﹣1) D.(1,0)
3.(3分)如图,该硬币边缘镌刻的正九边形每个内角的度数是( )
A.120° B.135° C.140° D.144°
4.(3分)如图,点A的坐标为(1,3),O为坐标原点,将OA绕点A按逆时针方向旋转90°得到AO′,则点O′的坐标是( )
A.(4,﹣1) B.(﹣1,4) C.(4,2) D.(2,﹣4)
5.(3分)如图,在⊙O的内接四边形ABCD中,E为直径AB延长线上的一点,若∠D=120°,∠BCE=20°,则∠E的度数为( )
A.30° B.35° C.40° D.45°
6.(3分)已知点A(1,y1),B(2,y2)在抛物线y=﹣(x+1)2+2上,则下列结论正确的是( )
A.y1>y2>2 B.y2>y1>2 C.2>y1>y2 D.2>y2>y1
7.(3分)如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π B.3π C.2π D.2π
8.(3分)如图,点P是正六边形ABCDEF内一点,AB=4,当∠APB=90°时,连接PD,则线段PD的最小值是( )
A. B. C.6 D.
二、填空题(本题有6小题,每小题3分,共18分)
9.(3分)在⊙O中,弦AB=3,圆心角∠A0B=60°,则⊙O的半径为 .
10.(3分)把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为 .
11.(3分)某鱼塘养了1000条草鱼、500条鲤鱼、若干条鲫鱼,鱼塘主通过多次捕捞试验发现,捕捞到鲫鱼的频率稳定在0.25左右.若鱼塘主随机在鱼塘里捕捞一条鱼,捕捞到草鱼的概率约为 .
12.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕点C顺时针旋转得到△A1B1C(点A与A1点B与B1对应).当点A,B1,A1在同一直线上时,AB1的长为 .
13.(3分)如图,△ABC是圆O的内接三角形,延长BO交AC于点D,OE⊥BC,垂足为点E,点F是OB上一点,OE=OF,若∠ABC=m∠OEF,∠ACB=n∠OEF,则m,n满足的关系式是 .
14.(3分)如图,嘉嘉用计算机编程模拟抛出的弹跳球落在斜面上反弹后的距离,当弹跳球以某种特定的角度从点P(0,1)处抛出后,弹跳球的运动轨迹是抛物线L,其最高点的坐标为(4,5).弹跳球落到斜面上的点A处反弹后,弹跳球的运动轨迹是抛物线L′,且开口大小和方向均与L相同,但最大高度只是抛物线L最大高度的.若点A与点P的高度相同,且点A在抛物线L′的对称轴的右侧,则抛物线L′的对称轴为直线 .
三、解答题(本题有8小题,共72分,各小题都必须写出解答过程)
15.(6分)已知二次函数y=ax2+bx+c的图象经过点A(﹣1,0),点B(0,5),点C(1,8).
(1)求函数表达式;
(2)当y=8时,求x的值.
16.(6分)如图,在⊙O中,弦AB、CD交于点E,且AB=CD.求证:DE=BE.
17.(8分)有A,B,C三种款式的帽子,E,F两种款式的围巾,小赵任意选一顶帽子和一条围巾.
(1)用恰当的方法列举出所有可能选中的结果;
(2)求小赵恰好选中她所喜欢的B款帽子和F款围巾的概率.
18.(8分)如图所示,把△ABC置于平面直角坐标系中,请你按下列要求分别画图:
(1)画出△ABC绕着原点O逆时针旋转90°得到的△A1B1C1;
(2)在(1)的基础上求点C经过的路径长.
19.(10分)超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量y(瓶)与每瓶售价x(元)之间满足一次函数关系(其中10≤x≤15,且x为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.
(1)求y与x之间的函数关系式;
(2)设超市销售该品牌洗手液每天销售利润为w元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?
20.(10分)如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作FE的垂线,垂足为点H,与BC交于点G.
(1)求证:AH垂直平分EF;
(2)若CG=2,BG=3,求AF的长.
21.(12分)已知二次函数y=ax2﹣2(a+1)x+4(a≠0).
(1)若二次函数过点(1,1)
①求二次函数的表达式;
②当y随x的增大而减小时,求x的取值范围.
(2)若点和点在该二次函数图象上,求的值.
22.(12分)如图,四边形ABCD内接于⊙O,AD为直径,AB=BC,BH⊥AD于H,AH=2,BH=4.
(1)求⊙O的半径;
(2)求四边形ABCD的面积;
(3)E是线段BD上一点,BE=BC,连接CE并延长交⊙O于F,求CF的长.
2024-2025学年浙江省丽水市文元教育集团九年级(上)期中数学试卷
参考答案
一、选择题(本题有10小题,每小题3分,共30分)
1.(3分)⊙O的半径为2cm,点P到圆心O的距离为,那么点A与⊙O的位置关系是( )
A.点P在圆内 B.点P在圆上 C.点P在圆外 D.点P在圆心
选:A.
2.(3分)二次函数y=x2+1图象的顶点坐标是( )
A.(0,1) B.(﹣1,0) C.(0,﹣1) D.(1,0)
选:A.
3.(3分)如图,该硬币边缘镌刻的正九边形每个内角的度数是( )
A.120° B.135° C.140° D.144°
选:C.
4.(3分)如图,点A的坐标为(1,3),O为坐标原点,将OA绕点A按逆时针方向旋转90°得到AO′,则点O′的坐标是( )
A.(4,﹣1) B.(﹣1,4) C.(4,2) D.(2,﹣4)
选:C.
5.(3分)如图,在⊙O的内接四边形ABCD中,E为直径AB延长线上的一点,若∠D=120°,∠BCE=20°,则∠E的度数为( )
A.30° B.35° C.40° D.45°
选:C.
6.(3分)已知点A(1,y1),B(2,y2)在抛物线y=﹣(x+1)2+2上,则下列结论正确的是( )
A.y1>y2>2 B.y2>y1>2 C.2>y1>y2 D.2>y2>y1
选:C.
7.(3分)如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π B.3π C.2π D.2π
选:A.
8.(3分)如图,点P是正六边形ABCDEF内一点,AB=4,当∠APB=90°时,连接PD,则线段PD的最小值是( )
A. B. C.6 D.
选:B.
二、填空题(本题有6小题,每小题3分,共18分)
9.(3分)在⊙O中,弦AB=3,圆心角∠A0B=60°,则⊙O的半径为 3 .
10.(3分)把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为 y=﹣(x+1)2+3 .
11.(3分)某鱼塘养了1000条草鱼、500条鲤鱼、若干条鲫鱼,鱼塘主通过多次捕捞试验发现,捕捞到鲫鱼的频率稳定在0.25左右.若鱼塘主随机在鱼塘里捕捞一条鱼,捕捞到草鱼的概率约为 .
12.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕点C顺时针旋转得到△A1B1C(点A与A1点B与B1对应).当点A,B1,A1在同一直线上时,AB1的长为 .
13.(3分)如图,△ABC是圆O的内接三角形,延长BO交AC于点D,OE⊥BC,垂足为点E,点F是OB上一点,OE=OF,若∠ABC=m∠OEF,∠ACB=n∠OEF,则m,n满足的关系式是 m+n=2 .
14.(3分)如图,嘉嘉用计算机编程模拟抛出的弹跳球落在斜面上反弹后的距离,当弹跳球以某种特定的角度从点P(0,1)处抛出后,弹跳球的运动轨迹是抛物线L,其最高点的坐标为(4,5).弹跳球落到斜面上的点A处反弹后,弹跳球的运动轨迹是抛物线L′,且开口大小和方向均与L相同,但最大高度只是抛物线L最大高度的.若点A与点P的高度相同,且点A在抛物线L′的对称轴的右侧,则抛物线L′的对称轴为直线 x=6 .
三、解答题(本题有8小题,共72分,各小题都必须写出解答过程)
15.(6分)已知二次函数y=ax2+bx+c的图象经过点A(﹣1,0),点B(0,5),点C(1,8).
(1)求函数表达式;
(2)当y=8时,求x的值.
【解答】解:(1)根据题意得,
解得,
∴抛物线解析式为y=﹣x2+4x+5;
(2)当y=8时,﹣x2+4x+5=8,
解得x1=1,x2=3,
即x的值为1或3.
16.(6分)如图,在⊙O中,弦AB、CD交于点E,且AB=CD.求证:DE=BE.
【解答】证明:∵AB=CD,
∴,
∴,
即,
∴AD=CB,
在△AED和△CEB中,
,
∴△AED≌△CEB(AAS),
∴DE=BE.
17.(8分)有A,B,C三种款式的帽子,E,F两种款式的围巾,小赵任意选一顶帽子和一条围巾.
(1)用恰当的方法列举出所有可能选中的结果;
(2)求小赵恰好选中她所喜欢的B款帽子和F款围巾的概率.
【解答】解:(1)列表如下:
围巾帽子 E F
A (A,E) (A,F)
B (B,E) (B,F)
C (C,E) (C,F)
(2)由(1)得:共有6个等可能的结果,小赵恰好选中她所喜欢的B款帽子和F款围巾的结果有1个,
∴小赵恰好选中她所喜欢的B款帽子和F款围巾的概率为.
18.(8分)如图所示,把△ABC置于平面直角坐标系中,请你按下列要求分别画图:
(1)画出△ABC绕着原点O逆时针旋转90°得到的△A1B1C1;
(2)在(1)的基础上求点C经过的路径长.
【解答】解:(1)如图:△A1B1C1即为所求;
(2),
∴点C经过的路径长为.
19.(10分)超市销售某品牌洗手液,进价为每瓶10元.在销售过程中发现,每天销售量y(瓶)与每瓶售价x(元)之间满足一次函数关系(其中10≤x≤15,且x为整数),当每瓶洗手液的售价是12元时,每天销售量为90瓶;当每瓶洗手液的售价是14元时,每天销售量为80瓶.
(1)求y与x之间的函数关系式;
(2)设超市销售该品牌洗手液每天销售利润为w元,当每瓶洗手液的售价定为多少元时,超市销售该品牌洗手液每天销售利润最大,最大利润是多少元?
【解答】解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),根据题意得:
,
解得:,
∴y与x之间的函数关系为y=﹣5x+150;
(2)根据题意得:w=(x﹣10)(﹣5x+150)=﹣5(x﹣20)2+500,
∵a=﹣5<0,
∴抛物线开口向下,w有最大值,
∴当x<20时,w随着x的增大而增大,
∵10≤x≤15且x为整数,
∴当x=15时,w有最大值,
即:w=﹣5×(15﹣20)2+500=375,
答:当每瓶洗手液的售价定为15元时,超市销售该品牌洗手液每天销售利润最大,最大利润为375元.
20.(10分)如图,点E在正方形ABCD的边CD上,将△ADE绕点A顺时针旋转90°到△ABF的位置,连接EF,过点A作FE的垂线,垂足为点H,与BC交于点G.
(1)求证:AH垂直平分EF;
(2)若CG=2,BG=3,求AF的长.
【解答】(1)证明:∵将△ADE绕点A顺时针旋转90°得到△ABF,
∴AF=AE,
∵AH⊥FE于点H,
∴FH=EH,
∴AH垂直平分EF.
(2)解:连接EG,
∵四边形ABCD是正方形,CG=2,BG=3,
∴∠ABC=∠C=∠D=90°,AB=AD=CD=BC=CG+BG=2+3=5,
由旋转得BF=DE,∠ABF=∠D=90°,
∴∠ABF+∠ABC=180°,
∴点F在CB的延长线上,
∵CG2+CE2=EG2,且CE=5﹣DE=5﹣BF,EG=FG=3+BF,
∴22+(5﹣BF)2=(3+BF)2,
解得BF=,
∴AF===,
∴AF的长是.
21.(12分)已知二次函数y=ax2﹣2(a+1)x+4(a≠0).
(1)若二次函数过点(1,1)
①求二次函数的表达式;
②当y随x的增大而减小时,求x的取值范围.
(2)若点和点在该二次函数图象上,求的值.
【解答】解:(1)①∵二次函数过点(1,1),
∴1=a﹣2(a+1)+4.
∴a=1.
∴二次函数的表达式为y=x2﹣4x+4.
②由①y=x2﹣4x+4=(x﹣2)2,
∴当x<2时,y随x的增大而减小.
∴当y随x的增大而减小时,x<2.
(2)∵y=ax2﹣2(a+1)x+4(a≠0),
∴抛物线对称轴为直线x=﹣=1+.
∵点P(,b)和点Q(+n,b)关于对称轴对称,
∴=1+.
∴n=2.
把P(,b)代入函数解析式得:a×﹣2(a+1)×+4=b,
解得b=2﹣.
∴(+b)2+n2=(+2﹣)2+22=8.
22.(12分)如图,四边形ABCD内接于⊙O,AD为直径,AB=BC,BH⊥AD于H,AH=2,BH=4.
(1)求⊙O的半径;
(2)求四边形ABCD的面积;
(3)E是线段BD上一点,BE=BC,连接CE并延长交⊙O于F,求CF的长.
【解答】解:(1)如图,连接OB,设⊙O半径为r,
在Rt△BOH中,OH=r﹣2,OB=r,BH=4,由勾股定理得:
r2=42+(r﹣2)2,
解得:r=5,
∴⊙O的半径为5;
(2)如图,过B作BG⊥DC,交DC延长线于点G,
∵AB=BC,
∴∠ADB=∠BDC,
∴BD是∠ADC的平分线,
∴BH=BG=4,DH=DG=10﹣2=8,
∵AB=BC,BH=BG,
∴△ABH≌△BCG(HL),
∴AH=CG =2,
∴CD=8﹣2=6,
S四边形ABCD=S△ABD+S△BCD=+=32.
(3)如图,连接DF,过C作CG⊥BD于点G,则∠BGC=90°,
由(2)得:OH=3,BH=4,
∴AH=2,
∴,同理得:,
∵AB=BC,BC=BE,
∴,
∴,
∵∠BGC=∠AMO=90°,∠CBG=∠MAO,
∴△BGC∽△AMO,
∴,
∴,即,
∴,
由勾股定理得:,
∴,
在Rt△CGE中,由勾股定理得:,
∵∠CBE=∠EFD,∠BCE=∠FDE,
∴△BCE∽△FDE,
∴,
∴,则,
∵BE=BC,
∴∠BCE=∠BEC=∠FED,
∴∠FED=∠FDE,
∴,
∴.
同课章节目录
