2024—2025学年苏科版数学八年级上期末复习试题(含答案)
文档属性
| 名称 | 2024—2025学年苏科版数学八年级上期末复习试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 399.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 22:00:50 | ||
图片预览


文档简介
苏科版数学八年级上期末复习试题
一.选择题(共10小题)
1.第十九届亚运会于2023年9月23日至10月8日在杭州隆重举行,下列图标是亚运会上常见的运动图标,其中是轴对称图形的是( )
A. B. C. D.
2.已知,|b+1|=0,则点P(a,b)关于原点对称的点的坐标是( )
A.(2,﹣1) B.(﹣2,﹣1) C.(﹣2,1) D.(2,1)
3.下列实数,,,0,﹣π,0.010010001…(每两个1之间依次增加1个0)中,无理数有( )
A.5个 B.4个 C.3个 D.2个
4.已知一次函数y=ax+b和y=bx+a(a,b为常数且a≠b),那么它们的图象可能是( )
A. B. C. D.
5.如图,在△ABC和△DEF中,点A,E,B,D在同一直线上,∠ABC=∠DEF,AE=BD,若只添加一个条件,不能判定△ABC≌△DEF的是( )
A.AC=DF B.BC=EF C.∠C=∠F D.∠BAC=∠EDF
6.在△ABC中,下列条件:①∠A=∠C﹣∠B;②∠A:∠B:∠C=3:4:5;③a2=b2﹣c2;④a=2,b=2,c=2.能判断△ABC是直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
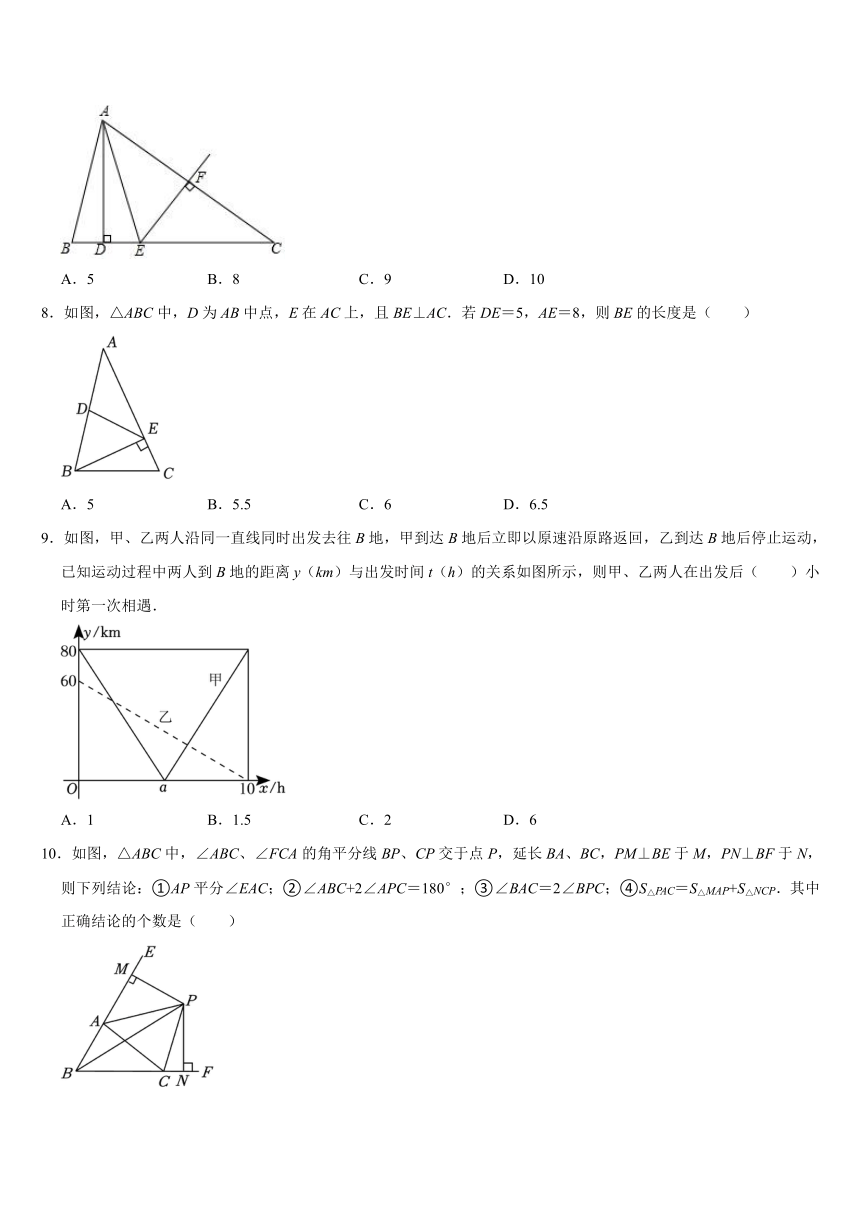
7.如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC=6,则DC为( )
A.5 B.8 C.9 D.10
8.如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=5,AE=8,则BE的长度是( )
A.5 B.5.5 C.6 D.6.5
9.如图,甲、乙两人沿同一直线同时出发去往B地,甲到达B地后立即以原速沿原路返回,乙到达B地后停止运动,已知运动过程中两人到B地的距离y(km)与出发时间t(h)的关系如图所示,则甲、乙两人在出发后( )小时第一次相遇.
A.1 B.1.5 C.2 D.6
10.如图,△ABC中,∠ABC、∠FCA的角平分线BP、CP交于点P,延长BA、BC,PM⊥BE于M,PN⊥BF于N,则下列结论:①AP平分∠EAC;②∠ABC+2∠APC=180°;③∠BAC=2∠BPC;④S△PAC=S△MAP+S△NCP.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题)
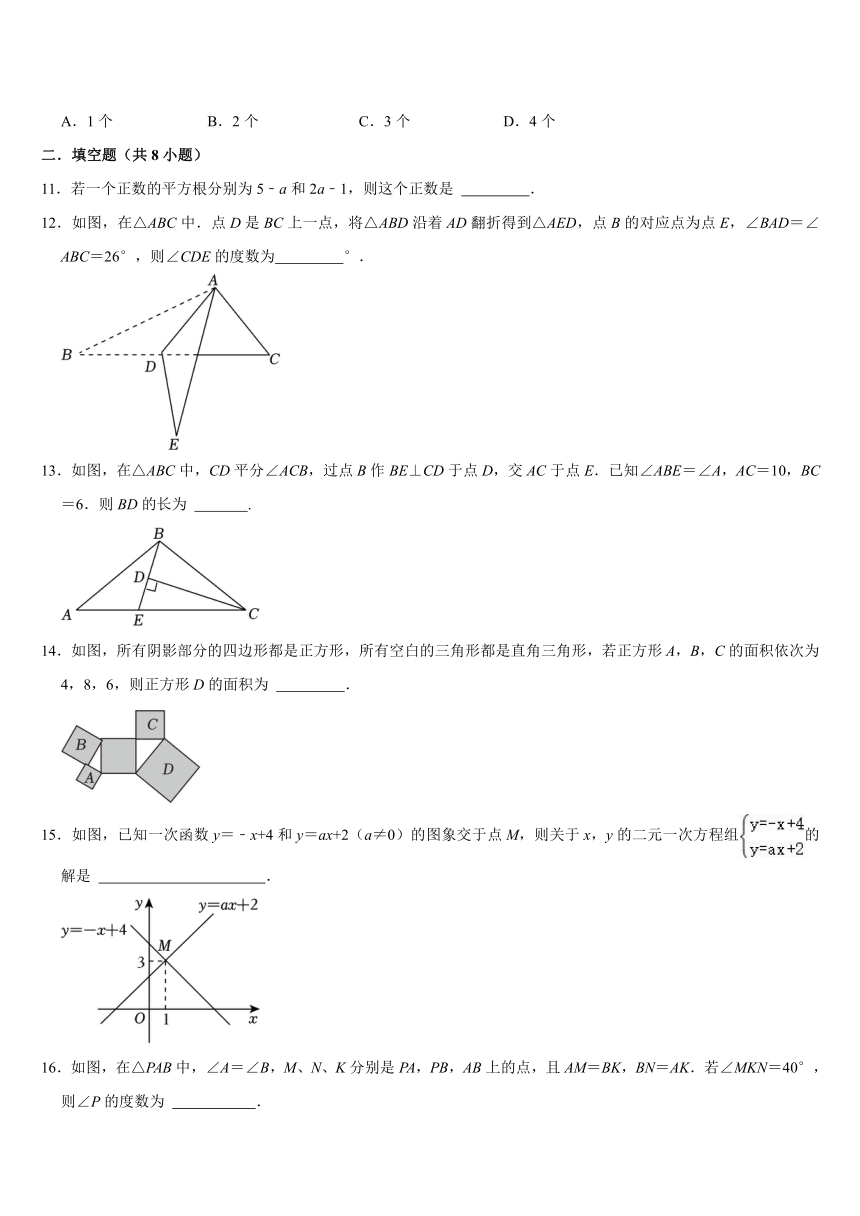
11.若一个正数的平方根分别为5﹣a和2a﹣1,则这个正数是 .
12.如图,在△ABC中.点D是BC上一点,将△ABD沿着AD翻折得到△AED,点B的对应点为点E,∠BAD=∠ABC=26°,则∠CDE的度数为 °.
13.如图,在△ABC中,CD平分∠ACB,过点B作BE⊥CD于点D,交AC于点E.已知∠ABE=∠A,AC=10,BC=6.则BD的长为 .
14.如图,所有阴影部分的四边形都是正方形,所有空白的三角形都是直角三角形,若正方形A,B,C的面积依次为4,8,6,则正方形D的面积为 .
15.如图,已知一次函数y=﹣x+4和y=ax+2(a≠0)的图象交于点M,则关于x,y的二元一次方程组的解是 .
16.如图,在△PAB中,∠A=∠B,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为 .
17.如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长25m,顶端A在AC上运动,量得滑杆底端B距点C的距离为15m,当底端B向右移动5m到达点D,顶端A到达点E时,求滑杆顶端A下滑 米.
18.如图,在△ABC中,AB=BC,BE、CF分别是AC、AB边上的高,在BE上取点D,使BD=CA,在射线CF上取点G,使CG=BA,连接AD、AG,若∠DAE=38°,∠EBC=20°,则∠GAB= °.
三.解答题(共10小题)
19.计算.
(1); (2).
20.已知6a+34的立方根是4,5a+b﹣2的算术平方根是5,c是9的算术平方根.
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
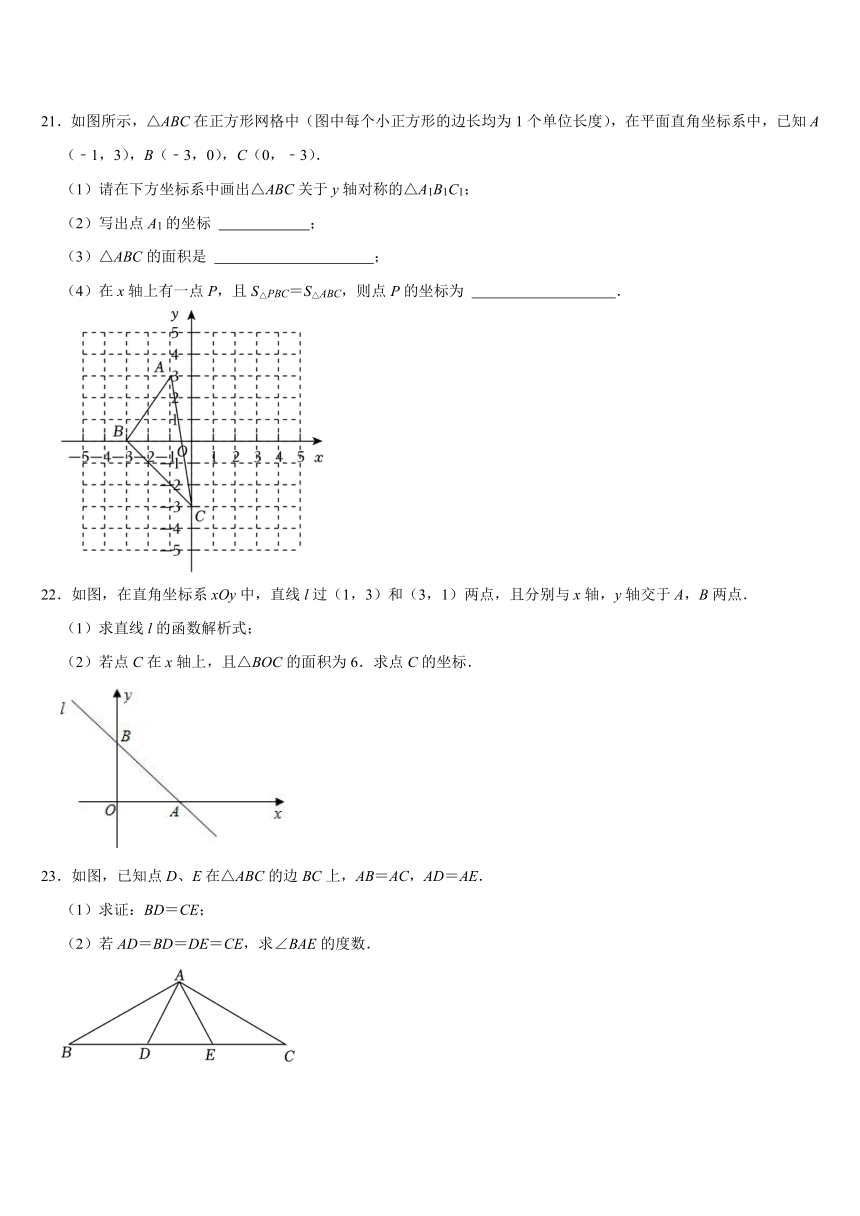
21.如图所示,△ABC在正方形网格中(图中每个小正方形的边长均为1个单位长度),在平面直角坐标系中,已知A(﹣1,3),B(﹣3,0),C(0,﹣3).
(1)请在下方坐标系中画出△ABC关于y轴对称的△A1B1C1;
(2)写出点A1的坐标 ;
(3)△ABC的面积是 ;
(4)在x轴上有一点P,且S△PBC=S△ABC,则点P的坐标为 .
22.如图,在直角坐标系xOy中,直线l过(1,3)和(3,1)两点,且分别与x轴,y轴交于A,B两点.
(1)求直线l的函数解析式;
(2)若点C在x轴上,且△BOC的面积为6.求点C的坐标.
23.如图,已知点D、E在△ABC的边BC上,AB=AC,AD=AE.
(1)求证:BD=CE;
(2)若AD=BD=DE=CE,求∠BAE的度数.
24.如图,OB、OC为△ABC的角平分线,EF∥BC交AB、AC于E、F,△AEF的周长为16,BC长为8,求△ABC的周长.
25.如图,AD是△ABC的角平分线,且AB=AC,过点D作DE∥AC,交AB于E点.
(1)求证:△ADE是等腰三角形;
(2)若AB=10,BC=12,求AD的长.
26.如图,已知A,D,C,E在同一直线上,BC和DF相交于点O,AD=CE,AB∥DF,AB=DF.
(1)求证:△ABC≌△DFE;
(2)连接CF,若∠BCF=54°,∠DFC=20°,求∠DFE的度数.
27.如图1,平面直角坐标系中,直线y=﹣x+m交x轴于点A(4,0),交y轴正半轴于点B,直线AC交y轴负半轴于点C,且BC=AB.
(1)求△ABC的面积.
(2)P为线段AB(不含A,B两点)上一动点.
①如图2,过点P作y轴的平行线交线段AC于点Q,记四边形APOQ的面积为S,点P的横坐标为t,当S=时,求t的值.
②M为线段BA延长线上一点,且AM=BP,在直线AC上是否存在点N,使得△PMN是以PM为直角边的等腰直角三角形?若存在,直接写出点N的坐标;若不存在,请说明理由.
28.(1)如图①,已知:△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;
(2)拓展:如图②,将(1)中的条件改为:△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
参考答案
一.选择题(共10小题)
1.A.
2.C.
3.D.
4.B.
5.A.
6.C.
7.A.
8.C.
9.C.
10.D.
二.填空题(共8小题)
11.81.
12.76.
13.2.
14.18.
15..
16.100°.
17.5.
18.58.
三.解答题(共10小题)
19.解:(1)原式=﹣2﹣(2﹣)+1
=﹣2﹣2++1
=﹣3;
(2)原式=5﹣4+4﹣5+9
=13﹣4.
20.解:(1)∵43=64,
∴6a+34=64,
∴a=5;
∵52=25,
∴5a+b﹣2=25,
又∵a=5,
∴b=2;
∵32=9,
∴c=3;
(2)把:a=5,b=2,c=3代入3a﹣b+c得:
3×5﹣2+3=16,
∵(±4)2=16,
∴3a﹣b+c的平方根是:±4.
21.解:(1)如图,△A1B1C1即为所求.
(2)由图可得,点A1的坐标为(1,3).
(3)△ABC的面积是==.
(4)设点P的坐标为(m,0),
∵S△PBC=S△ABC,
∴=,
解得m=2或﹣8,
∴点P的坐标为(2,0)或(﹣8,0).
22.解:(1)设直线l的函数关系式为y=kx+b(k≠0),
把(3,1),(1,3)代入得,
解方程组得,
∴直线l的函数关系式为y=﹣x+4;
(2)设C(x,0),
当x=0时,y=﹣x+4=4,
∴B(0,4),
∴OB=4,
∵△BOC的面积为6,
∴=6,
∴OC=3,
∴C(3,0)或(﹣3,0).
23.(1)证明:如图,过点A作AF⊥BC于F.
∵AB=AC,AD=AE.
∴BF=CF,DF=EF,
∴BD=CE.
(2)∵AD=DE=AE,
∴△ADE是等边三角形,
∴∠DAE=∠ADE=60°.
∵AD=BD,
∴∠DAB=∠DBA.
∴∠DAB=∠ADE=30°.
∴∠BAE=∠BAD+∠DAE=90°.
24.解:∵OB平分∠ABC,
∴∠ABO=∠CBO,
∵EF∥BC,
∴∠CBO=∠EBO,
∴∠ABO=∠EOB,
∴BE=OE,
同理可得,CF=OF,
∵△AEF的周长为16,
∴AE+OE+OF+AF=AE+BE+CF+AF=AB+AC=16,
∵BC=8,
∴△ABC的周长=16+8=24.
25.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴EA=ED,
∴△ADE是等腰三角形;
(2)解:∵AB=AC,AD平分∠BAC,
∴∠ADB=90°,BD=CD=BC=6,
在Rt△ABD中,AB=10,
∴AD===8.
26.(1)证明:∵AB∥DF,
∴∠A=∠EDF,
∵AD=CE,
∴AD+CD=CE+CD,
即AC=DE,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(SAS);
(2)解:∵∠BCF=54°,∠DFC=20°,
∴∠DOC=∠BCF+∠DFC=54°+20°=74°,
∵AB∥DF,
∴∠B=∠DOC=74°,
∵△ABC≌△DFE,
∴∠DFE=∠B=74°.
27.解:(1)把A(4,0)代入得:m=3,
一次函数解析式为,
令x=0,得y=3,
∴B(0,3),
在Rt△AOB中,AB2=OA2+OB2,
∴AB=5,
∵BC=AB=5,
∴C(0,﹣2),
∴;
(2)①设,
∴P在线段AB上,
∴0<t<4,
设直线AC的解析式为y=kx+b,代入A(4,0),C(0,﹣2)得,
∴,
∴,
又∵PQ∥y轴,则,
∴,
∴S四边形APOQ=S△AOP+S△AOQ=AO×|yP|+AO×|yQ|=×4×PQ=×4×(5﹣t)=,
又∵,
∴,解得t=1;
②如图所示,当N点在x轴下方时,
∵BP=AM,
∴BP+AP=AM+AP=AB,
∴PM=AB=5,
∵△PMN是以PM为直角边的等腰直角三角形,
当∠NPM=90°时,PN=PM=5,,
设,
过P点作直线M'N'∥x轴,作MM'⊥M'N',NN'⊥M'N',
∴MM'∥OB,
∴∠ABO=∠PMM',
在△AOB与△PM'M中,
,
∴△AOB≌△PM'M(AAS),
∴MM'=OB=3,PM'=OA=4,
∵∠NPN'+∠MPM'=90°,∠NPN'+∠N'NP=90°,
∴∠MPM'=∠N'NP,
在△PNN'与△MPM'中,
,
∴△PNN'≌△MPM'(AAS),
∴PN'=MM'=3,NN'=PM'=4,
∴M'N'=7,作MH⊥NN',则NH=1,
∵,
∴,
∴M在直线AB上,
∴,
,
,
a=﹣1,
∴,
∴.
当N点在x轴上方时,点N'与关于A(4,0)对称,
则,即,
综上:存在一点或使△PMN是以PM为直角边的等腰直角三角形.
28.(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)解:结论DE=BD+CE成立;理由如下:
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(3)解:∵∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,
∴∠CAE=∠ABD,
在△ABD和△CEA中,,
∴△ABD≌△CEA(AAS),
∴S△ABD=S△CEA,
设△ABC的底边BC上的高为h,则△ACF的底边CF上的高为h,
∴S△ABC=BC h=12,S△ACF=CF h,
∵BC=2CF,
∴S△ACF=6,
∵S△ACF=S△CEF+S△CEA=S△CEF+S△ABD=6,
∴△ABD与△CEF的面积之和为6.
一.选择题(共10小题)
1.第十九届亚运会于2023年9月23日至10月8日在杭州隆重举行,下列图标是亚运会上常见的运动图标,其中是轴对称图形的是( )
A. B. C. D.
2.已知,|b+1|=0,则点P(a,b)关于原点对称的点的坐标是( )
A.(2,﹣1) B.(﹣2,﹣1) C.(﹣2,1) D.(2,1)
3.下列实数,,,0,﹣π,0.010010001…(每两个1之间依次增加1个0)中,无理数有( )
A.5个 B.4个 C.3个 D.2个
4.已知一次函数y=ax+b和y=bx+a(a,b为常数且a≠b),那么它们的图象可能是( )
A. B. C. D.
5.如图,在△ABC和△DEF中,点A,E,B,D在同一直线上,∠ABC=∠DEF,AE=BD,若只添加一个条件,不能判定△ABC≌△DEF的是( )
A.AC=DF B.BC=EF C.∠C=∠F D.∠BAC=∠EDF
6.在△ABC中,下列条件:①∠A=∠C﹣∠B;②∠A:∠B:∠C=3:4:5;③a2=b2﹣c2;④a=2,b=2,c=2.能判断△ABC是直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,若△ABC周长为16,AC=6,则DC为( )
A.5 B.8 C.9 D.10
8.如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=5,AE=8,则BE的长度是( )
A.5 B.5.5 C.6 D.6.5
9.如图,甲、乙两人沿同一直线同时出发去往B地,甲到达B地后立即以原速沿原路返回,乙到达B地后停止运动,已知运动过程中两人到B地的距离y(km)与出发时间t(h)的关系如图所示,则甲、乙两人在出发后( )小时第一次相遇.
A.1 B.1.5 C.2 D.6
10.如图,△ABC中,∠ABC、∠FCA的角平分线BP、CP交于点P,延长BA、BC,PM⊥BE于M,PN⊥BF于N,则下列结论:①AP平分∠EAC;②∠ABC+2∠APC=180°;③∠BAC=2∠BPC;④S△PAC=S△MAP+S△NCP.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题)
11.若一个正数的平方根分别为5﹣a和2a﹣1,则这个正数是 .
12.如图,在△ABC中.点D是BC上一点,将△ABD沿着AD翻折得到△AED,点B的对应点为点E,∠BAD=∠ABC=26°,则∠CDE的度数为 °.
13.如图,在△ABC中,CD平分∠ACB,过点B作BE⊥CD于点D,交AC于点E.已知∠ABE=∠A,AC=10,BC=6.则BD的长为 .
14.如图,所有阴影部分的四边形都是正方形,所有空白的三角形都是直角三角形,若正方形A,B,C的面积依次为4,8,6,则正方形D的面积为 .
15.如图,已知一次函数y=﹣x+4和y=ax+2(a≠0)的图象交于点M,则关于x,y的二元一次方程组的解是 .
16.如图,在△PAB中,∠A=∠B,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为 .
17.如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长25m,顶端A在AC上运动,量得滑杆底端B距点C的距离为15m,当底端B向右移动5m到达点D,顶端A到达点E时,求滑杆顶端A下滑 米.
18.如图,在△ABC中,AB=BC,BE、CF分别是AC、AB边上的高,在BE上取点D,使BD=CA,在射线CF上取点G,使CG=BA,连接AD、AG,若∠DAE=38°,∠EBC=20°,则∠GAB= °.
三.解答题(共10小题)
19.计算.
(1); (2).
20.已知6a+34的立方根是4,5a+b﹣2的算术平方根是5,c是9的算术平方根.
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
21.如图所示,△ABC在正方形网格中(图中每个小正方形的边长均为1个单位长度),在平面直角坐标系中,已知A(﹣1,3),B(﹣3,0),C(0,﹣3).
(1)请在下方坐标系中画出△ABC关于y轴对称的△A1B1C1;
(2)写出点A1的坐标 ;
(3)△ABC的面积是 ;
(4)在x轴上有一点P,且S△PBC=S△ABC,则点P的坐标为 .
22.如图,在直角坐标系xOy中,直线l过(1,3)和(3,1)两点,且分别与x轴,y轴交于A,B两点.
(1)求直线l的函数解析式;
(2)若点C在x轴上,且△BOC的面积为6.求点C的坐标.
23.如图,已知点D、E在△ABC的边BC上,AB=AC,AD=AE.
(1)求证:BD=CE;
(2)若AD=BD=DE=CE,求∠BAE的度数.
24.如图,OB、OC为△ABC的角平分线,EF∥BC交AB、AC于E、F,△AEF的周长为16,BC长为8,求△ABC的周长.
25.如图,AD是△ABC的角平分线,且AB=AC,过点D作DE∥AC,交AB于E点.
(1)求证:△ADE是等腰三角形;
(2)若AB=10,BC=12,求AD的长.
26.如图,已知A,D,C,E在同一直线上,BC和DF相交于点O,AD=CE,AB∥DF,AB=DF.
(1)求证:△ABC≌△DFE;
(2)连接CF,若∠BCF=54°,∠DFC=20°,求∠DFE的度数.
27.如图1,平面直角坐标系中,直线y=﹣x+m交x轴于点A(4,0),交y轴正半轴于点B,直线AC交y轴负半轴于点C,且BC=AB.
(1)求△ABC的面积.
(2)P为线段AB(不含A,B两点)上一动点.
①如图2,过点P作y轴的平行线交线段AC于点Q,记四边形APOQ的面积为S,点P的横坐标为t,当S=时,求t的值.
②M为线段BA延长线上一点,且AM=BP,在直线AC上是否存在点N,使得△PMN是以PM为直角边的等腰直角三角形?若存在,直接写出点N的坐标;若不存在,请说明理由.
28.(1)如图①,已知:△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;
(2)拓展:如图②,将(1)中的条件改为:△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
参考答案
一.选择题(共10小题)
1.A.
2.C.
3.D.
4.B.
5.A.
6.C.
7.A.
8.C.
9.C.
10.D.
二.填空题(共8小题)
11.81.
12.76.
13.2.
14.18.
15..
16.100°.
17.5.
18.58.
三.解答题(共10小题)
19.解:(1)原式=﹣2﹣(2﹣)+1
=﹣2﹣2++1
=﹣3;
(2)原式=5﹣4+4﹣5+9
=13﹣4.
20.解:(1)∵43=64,
∴6a+34=64,
∴a=5;
∵52=25,
∴5a+b﹣2=25,
又∵a=5,
∴b=2;
∵32=9,
∴c=3;
(2)把:a=5,b=2,c=3代入3a﹣b+c得:
3×5﹣2+3=16,
∵(±4)2=16,
∴3a﹣b+c的平方根是:±4.
21.解:(1)如图,△A1B1C1即为所求.
(2)由图可得,点A1的坐标为(1,3).
(3)△ABC的面积是==.
(4)设点P的坐标为(m,0),
∵S△PBC=S△ABC,
∴=,
解得m=2或﹣8,
∴点P的坐标为(2,0)或(﹣8,0).
22.解:(1)设直线l的函数关系式为y=kx+b(k≠0),
把(3,1),(1,3)代入得,
解方程组得,
∴直线l的函数关系式为y=﹣x+4;
(2)设C(x,0),
当x=0时,y=﹣x+4=4,
∴B(0,4),
∴OB=4,
∵△BOC的面积为6,
∴=6,
∴OC=3,
∴C(3,0)或(﹣3,0).
23.(1)证明:如图,过点A作AF⊥BC于F.
∵AB=AC,AD=AE.
∴BF=CF,DF=EF,
∴BD=CE.
(2)∵AD=DE=AE,
∴△ADE是等边三角形,
∴∠DAE=∠ADE=60°.
∵AD=BD,
∴∠DAB=∠DBA.
∴∠DAB=∠ADE=30°.
∴∠BAE=∠BAD+∠DAE=90°.
24.解:∵OB平分∠ABC,
∴∠ABO=∠CBO,
∵EF∥BC,
∴∠CBO=∠EBO,
∴∠ABO=∠EOB,
∴BE=OE,
同理可得,CF=OF,
∵△AEF的周长为16,
∴AE+OE+OF+AF=AE+BE+CF+AF=AB+AC=16,
∵BC=8,
∴△ABC的周长=16+8=24.
25.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴EA=ED,
∴△ADE是等腰三角形;
(2)解:∵AB=AC,AD平分∠BAC,
∴∠ADB=90°,BD=CD=BC=6,
在Rt△ABD中,AB=10,
∴AD===8.
26.(1)证明:∵AB∥DF,
∴∠A=∠EDF,
∵AD=CE,
∴AD+CD=CE+CD,
即AC=DE,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(SAS);
(2)解:∵∠BCF=54°,∠DFC=20°,
∴∠DOC=∠BCF+∠DFC=54°+20°=74°,
∵AB∥DF,
∴∠B=∠DOC=74°,
∵△ABC≌△DFE,
∴∠DFE=∠B=74°.
27.解:(1)把A(4,0)代入得:m=3,
一次函数解析式为,
令x=0,得y=3,
∴B(0,3),
在Rt△AOB中,AB2=OA2+OB2,
∴AB=5,
∵BC=AB=5,
∴C(0,﹣2),
∴;
(2)①设,
∴P在线段AB上,
∴0<t<4,
设直线AC的解析式为y=kx+b,代入A(4,0),C(0,﹣2)得,
∴,
∴,
又∵PQ∥y轴,则,
∴,
∴S四边形APOQ=S△AOP+S△AOQ=AO×|yP|+AO×|yQ|=×4×PQ=×4×(5﹣t)=,
又∵,
∴,解得t=1;
②如图所示,当N点在x轴下方时,
∵BP=AM,
∴BP+AP=AM+AP=AB,
∴PM=AB=5,
∵△PMN是以PM为直角边的等腰直角三角形,
当∠NPM=90°时,PN=PM=5,,
设,
过P点作直线M'N'∥x轴,作MM'⊥M'N',NN'⊥M'N',
∴MM'∥OB,
∴∠ABO=∠PMM',
在△AOB与△PM'M中,
,
∴△AOB≌△PM'M(AAS),
∴MM'=OB=3,PM'=OA=4,
∵∠NPN'+∠MPM'=90°,∠NPN'+∠N'NP=90°,
∴∠MPM'=∠N'NP,
在△PNN'与△MPM'中,
,
∴△PNN'≌△MPM'(AAS),
∴PN'=MM'=3,NN'=PM'=4,
∴M'N'=7,作MH⊥NN',则NH=1,
∵,
∴,
∴M在直线AB上,
∴,
,
,
a=﹣1,
∴,
∴.
当N点在x轴上方时,点N'与关于A(4,0)对称,
则,即,
综上:存在一点或使△PMN是以PM为直角边的等腰直角三角形.
28.(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)解:结论DE=BD+CE成立;理由如下:
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(3)解:∵∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,
∴∠CAE=∠ABD,
在△ABD和△CEA中,,
∴△ABD≌△CEA(AAS),
∴S△ABD=S△CEA,
设△ABC的底边BC上的高为h,则△ACF的底边CF上的高为h,
∴S△ABC=BC h=12,S△ACF=CF h,
∵BC=2CF,
∴S△ACF=6,
∵S△ACF=S△CEF+S△CEA=S△CEF+S△ABD=6,
∴△ABD与△CEF的面积之和为6.
同课章节目录
