2024—2025学年苏科版数学八年级上期末复习试题(含答案)
文档属性
| 名称 | 2024—2025学年苏科版数学八年级上期末复习试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 438.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 00:00:00 | ||
图片预览


文档简介
苏科版数学八年级上期末复习试题
一.选择题(共10小题)
1.“致中和,天地位焉,万物育焉.”对称美是我国古人和谐平衡思想的体现,常被运用于建筑、器物、绘画、标识等作品的设计上,使对称之美惊艳了千年的时光.下面四幅图是我国传统文化与艺术中的几个经典图案,其中不是轴对称图形的是( )
A. B. C. D.
2.已知点P的坐标为(x,y)且,则点P关于原点的对称点P′的坐标是( )
A.(﹣1,) B.(﹣1,) C.(1,) D.(1,)
3.下列各数中,属于无理数的是( )
A. B.0 C. D.
4.关于函数y=﹣x+3的图象,下列结论错误的是( )
A.图象经过一、二、四象限 B.与y轴的交点坐标为(3,0)
C.y随x的增大而减小 D.图象与两坐标轴相交所形成的直角三角形的面积为
5.如图,已知AC=DC,∠1=∠2,如果添加一个条件使△ABC≌△DEC,则添加的条件不可以是( )
A.∠A=∠D B.∠B=∠E C.BC=EC D.AB=DE
6.适合下列条件的△ABC中,直角三角形的个数为( )
①a=32,b=42,c=52;②(c+b)(c﹣b)=a;③∠A+∠B=∠C;④a=1,b=,c=.
A.1个 B.2个 C.3个 D.4
7.如图,△ABC的边长AB=8cm,AC=10cm,BC=4cm,作BC的垂直平分线交AC于D,则△ABD的周长为( )
A.18cm B.14cm C.20cm D.12cm
8.如图,在Rt△ABC中,BE为斜边AC上的中线,点D是AC下方一点,且AD=CD,连接DE,若BE=4,AD=5,则DE的长为( )
A.4.5 B. C.3.5 D.3
9.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;②乙走完全程用了36分钟;
③乙用16分钟追上甲;④乙到达终点时,甲离终点还有300米.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.如图,△ABC中,∠ABC、∠FCA的角平分线BP、CP交于点P,延长BA、BC,PM⊥BE于M,PN⊥BF于N,则下列结论:①AP平分∠EAC;②∠ABC+2∠APC=180°;③∠BAC=2∠BPC;④S△PAC=S△MAP+S△NCP.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题)
11.若有一个数m,它的平方根是a+1和2a﹣7,则m为 .
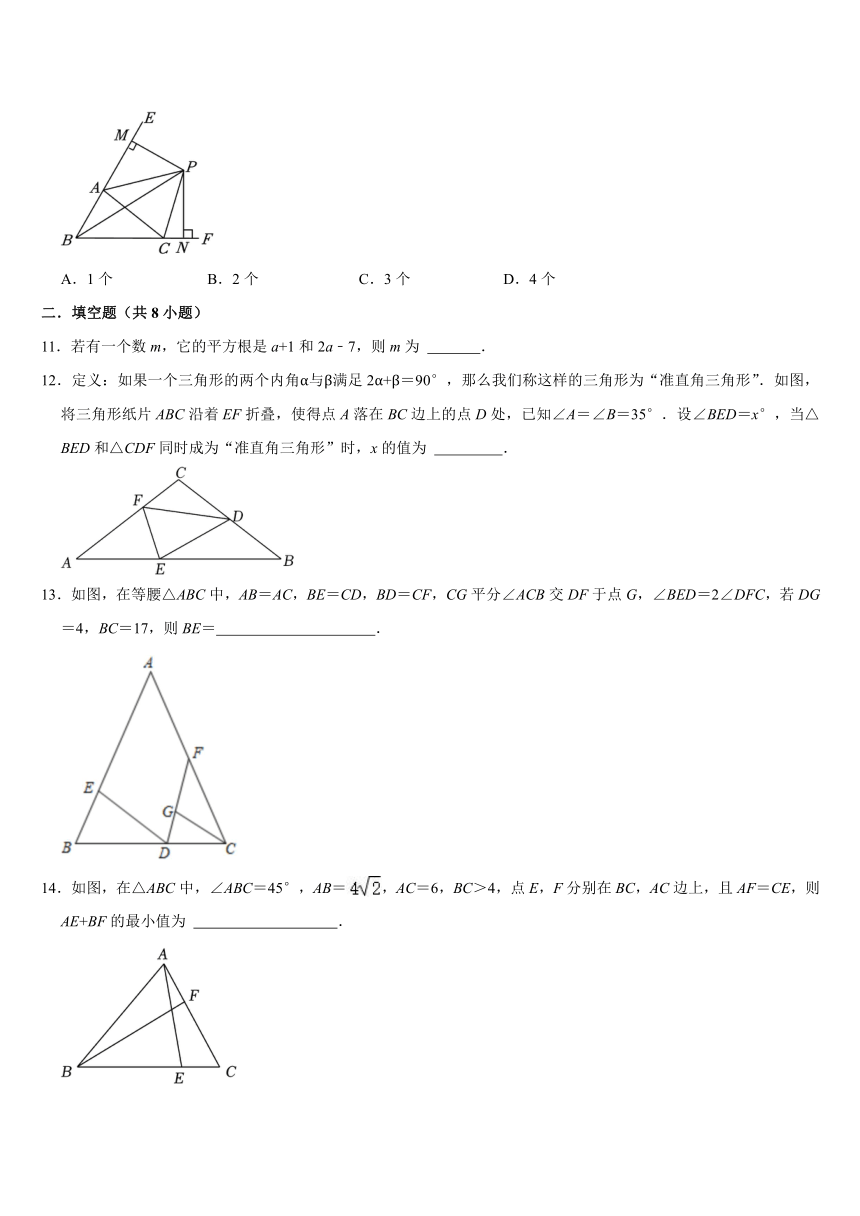
12.定义:如果一个三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准直角三角形”.如图,将三角形纸片ABC沿着EF折叠,使得点A落在BC边上的点D处,已知∠A=∠B=35°.设∠BED=x°,当△BED和△CDF同时成为“准直角三角形”时,x的值为 .
13.如图,在等腰△ABC中,AB=AC,BE=CD,BD=CF,CG平分∠ACB交DF于点G,∠BED=2∠DFC,若DG=4,BC=17,则BE= .
14.如图,在△ABC中,∠ABC=45°,AB=,AC=6,BC>4,点E,F分别在BC,AC边上,且AF=CE,则AE+BF的最小值为 .
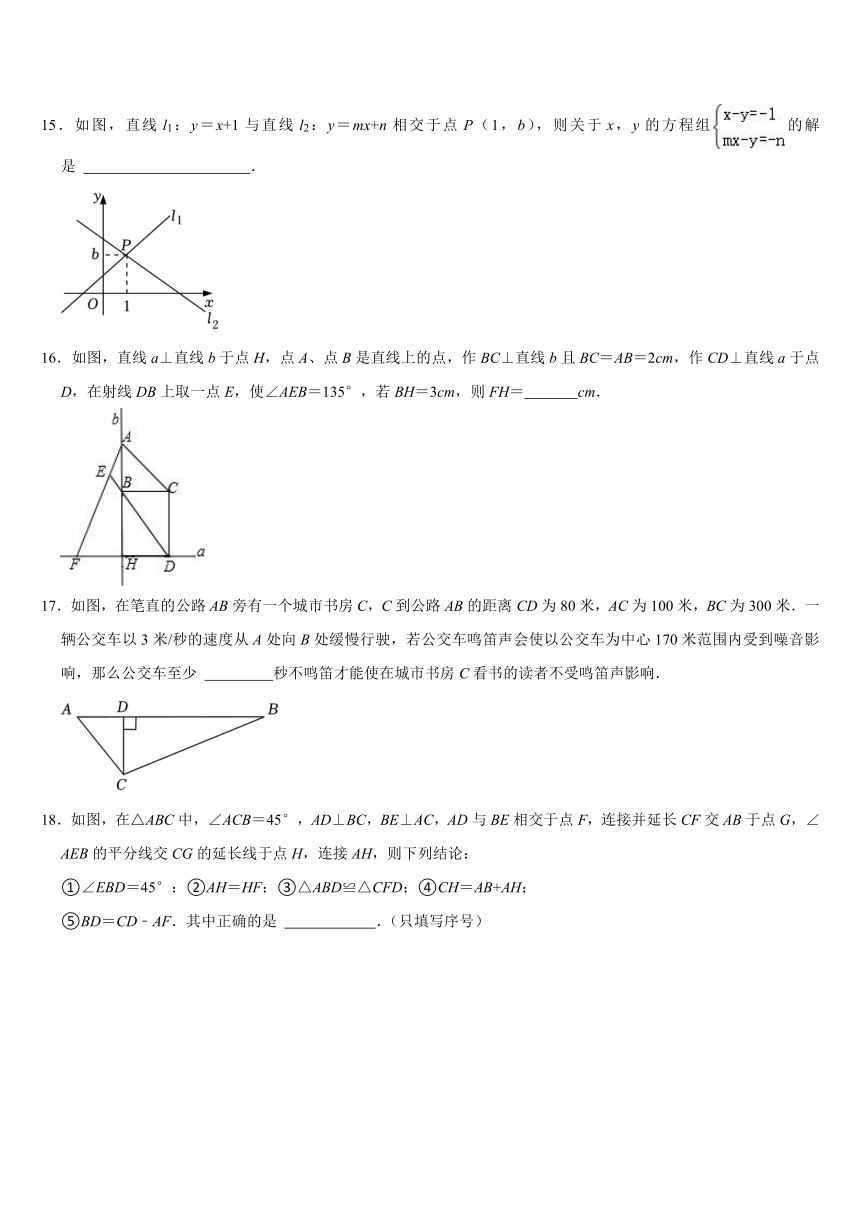
15.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解是 .
16.如图,直线a⊥直线b于点H,点A、点B是直线上的点,作BC⊥直线b且BC=AB=2cm,作CD⊥直线a于点D,在射线DB上取一点E,使∠AEB=135°,若BH=3cm,则FH= cm.
17.如图,在笔直的公路AB旁有一个城市书房C,C到公路AB的距离CD为80米,AC为100米,BC为300米.一辆公交车以3米/秒的速度从A处向B处缓慢行驶,若公交车鸣笛声会使以公交车为中心170米范围内受到噪音影响,那么公交车至少 秒不鸣笛才能使在城市书房C看书的读者不受鸣笛声影响.
18.如图,在△ABC中,∠ACB=45°,AD⊥BC,BE⊥AC,AD与BE相交于点F,连接并延长CF交AB于点G,∠AEB的平分线交CG的延长线于点H,连接AH,则下列结论:
①∠EBD=45°;②AH=HF;③△ABD≌△CFD;④CH=AB+AH;
⑤BD=CD﹣AF.其中正确的是 .(只填写序号)
三.解答题(共10小题)
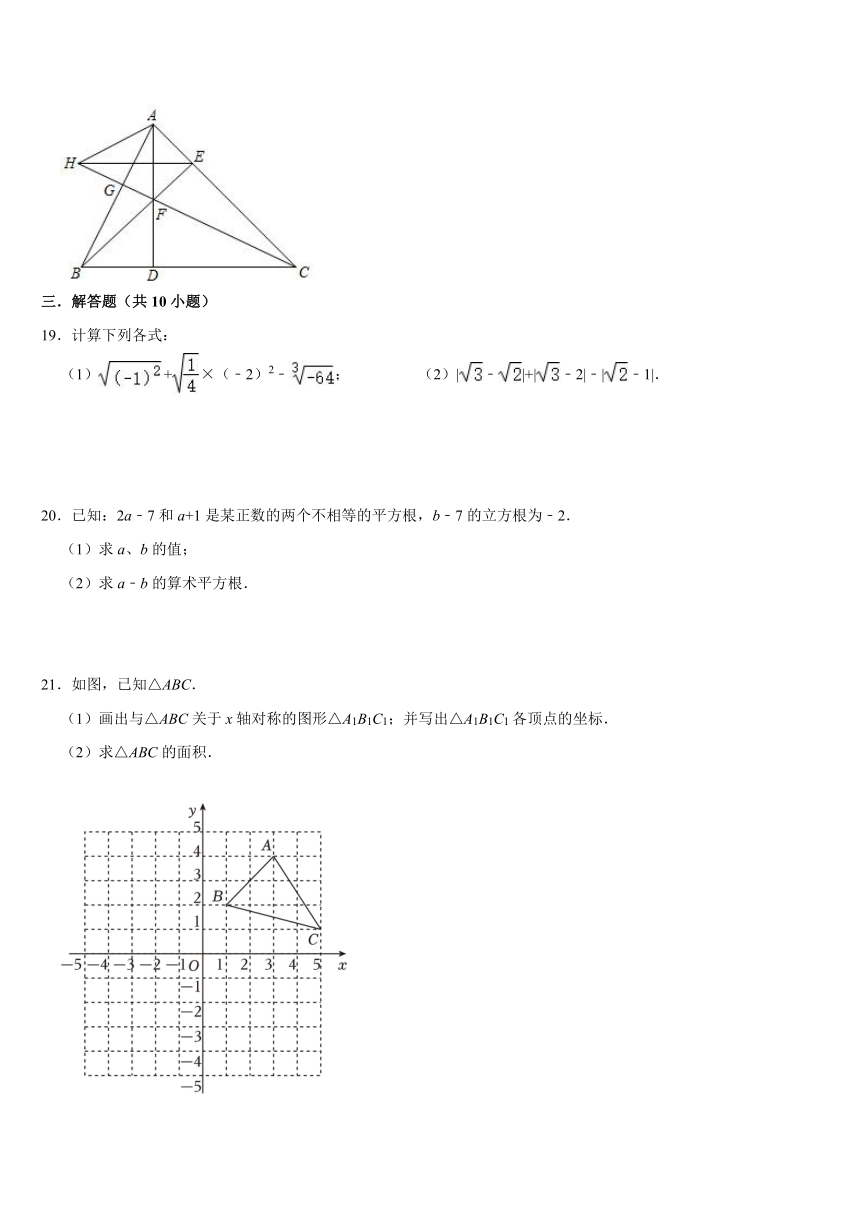
19.计算下列各式:
(1)+×(﹣2)2﹣; (2)|﹣|+|﹣2|﹣|﹣1|.
20.已知:2a﹣7和a+1是某正数的两个不相等的平方根,b﹣7的立方根为﹣2.
(1)求a、b的值;
(2)求a﹣b的算术平方根.
21.如图,已知△ABC.
(1)画出与△ABC关于x轴对称的图形△A1B1C1;并写出△A1B1C1各顶点的坐标.
(2)求△ABC的面积.
22.已知y+m与x﹣n成正比例关系.
(1)试说明y是x的一次函数;
(2)若当x=3时,y=3;当x=1时,y=﹣5.求该一次函数的表达式.
23.如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,且BD=BE,CD的垂直平分线MF交AC于F,交BC于M.
(1)求∠ADE的度数;
(2)证明△ADF是等边三角形;
(3)若MF的长为2,求AB的边长.
24.如图所示:∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E.
问:(1)图中有几个等腰三角形?为什么?
(2)BD,CE,DE之间存在着什么关系?请证明.
25.如图,BE是△ABC的角平分线,CD∥AB交BE延长线于点D.
(1)求证:CD=CB.
(2)过A作AF⊥AB交BD于F.若AE=AF,AC=4,BC=5,求AB的长.
26.已知:在△ABC中,D是AB边上的中点,DE⊥DF,垂足为D,DE与AC交于点E,DF与BC交于点F,过点A作AG∥BC与FD的延长线交于点G.
(1)求证:AG=BF;
(2)若EG=5,求EF的长.
27.如图1,直线y=x+6与x,y轴分别交于A,B两点,∠ABO的角平分线与x轴相交于点C.
(1)求点C的坐标;
(2)在直线BC上有两点M,N,△AMN是等腰直角三角形,∠MAN=90°,求点M的坐标;
(3)点P在y轴上,在平面上是否存在点Q,使以点A、B、P、Q为顶点的四边形为菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
28.已知∠MON=48°,点C是∠MON的平分线上一动点,点A,B分别是边ON,OM上动点,AB交OC于点D.
(1)如图1,当AB⊥OC,AC∥OB时,图中有 对全等的三角形,∠DAC= °.
(2)如图2,当AB平分∠OAC,且∠DAC=∠DCA时,求∠OBA的度数.
(3)如图3,当BA⊥ON于点A,在点C移动过程中,△ACD内有两个角相等时,求∠OAC的度数
参考答案
一.选择题(共10小题)
1.D.
2.D.
3.C.
4.B.
5.D.
6.B.
7.A.
8.D.
9.A.
10.D.
二.填空题(共8小题)
11.9.
12.20.
13..
14.2.
15..
16.1.
17.70.
18.①②③④⑤.
三.解答题(共10小题)
19.解:(1)原式=1+×4+4
=1+2+4
=7;
(2)原式=﹣+2﹣﹣(﹣1)
=﹣+2﹣﹣+1
=3﹣2.
20.解:(1)由题意可知:(2a﹣7)+(a+1)=0,
∴3a﹣6=0,
∴a=2,
∵b﹣7的立方根为﹣2
∴b﹣7=(﹣2)3,
∴b=﹣1;
(2)由(1)可知:a=2,b=﹣1,
∴a﹣b=2﹣(﹣1)=3,
∴a+b的算术平方根是.
21.解:(1)如图,△A1B1C1即为所求.
由图可得,A1(3,﹣4),B1(1,﹣2),C1(5,﹣1).
(2)△ABC的面积为=5.
22.解:(1)已知y+m与x﹣n成正比例,
设y+m=k(x﹣n)(k≠0),
y=kx﹣kn﹣m,
因为k≠0,所以y是x的一次函数;
(2)设函数关系式为y=kx+b,
因为x=3时,y=3;x=1时,y=﹣5,
所以,
解得,
所以函数关系式为y=4x﹣9.
23.(1)解:在△ABC中,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
又∵BD=BE,
∴∠BDE=∠BED=×(180°﹣∠B)=75°.
在△ABC中,
∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,
∴∠ADB=90°,
∴∠ADE=∠ADB﹣∠BDE=90°﹣75°=15°;
(2)证明:∵FM垂直平分DC,
∴DF=CF.
∵∠C=30°,
∴∠FDC=∠C=30°,
∴∠AFD=∠C+∠FDC=60°.
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAF=90°﹣∠C=60°,
∴∠AFD=∠DAF=∠ADF=60°,
∴△ADF是等边三角形.
(3)解:∵FM垂直平分DC,
∴∠FMC=90°.
∵∠C=30°,FM=2,
∴FC=2FM=4.
又DF=FC,
∴DF=4.
∵△ADF是等边三角形,
∴AF=DF=4,
∴AC=AF+CF=4+4=8.
又∵AB=AC,
∴AB=8.
24.(1)解:图中有2个等腰三角形即△BDF和△CEF,
理由:∵BF、CF分别平分∠ABC、∠ACB的外角,
∴∠DBF=∠CBF,∠FCE=∠FCG,
∵DE∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCG,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD,EF=CE,
∴△BDF和△CEF为等腰三角形;
(2)存在:BD﹣CE=DE,
证明:∵DF=BD,CE=EF,
∴BD﹣CE=FD﹣EF=DE.
25.(1)证明:∵BE平分∠ABC,
∴∠ABF=∠CBF,
∵CD∥AB,
∴∠ABD=∠D,
∴∠D=∠CBF,
∴CD=CB;
(2)解:∵AF⊥AB,
∴∠FAB=90°,
∴∠AFB+∠ABF=90°,
∵AF=AE,
∴∠AFB=∠AEF,
∵∠AEF=∠CEB,
∴∠AFB=∠CEB,
∵∠ABF=∠CBF,
∴∠CEB+∠CBF=90°,
∴∠ECB=180°﹣(∠CEB+∠CBF)=90°,
在Rt△ABC中,AC=4,BC=5,
∴AB===,
∴AB的长为.
26.(1)证明:∵D是AB边上的中点,
∴AD=BD,
∵AG∥BC,
∴∠GAD=∠B,
在△GAD和△FBD中,
,
∴△GAD≌△FBD(ASA),
∴AG=BF;
(2)解:由(1)可知:△GAD≌△FBD,
∴GD=FD,
∵DE⊥DF,
∴∠EDF=∠EDG=90°,
在△EDG和△EDF中,
,
∴△EDG≌△EDF(SAS),
∴EF=EG=5.
27.解:(1)对于直线y=x+6,令x=0,得到y=6,
∴B(0,6),
令y=0,得到x=﹣8,
∴A(﹣8,0).
∵A(﹣8,0),B(0,6),
∴OA=8,OB=6,
∵∠AOB=90°,
∴AB==10,
过点C作CH⊥AB于H,设OC=t,
∵BC平分∠ABO,∠AOB=90°,
∴CH=OC=t,
∵S△ABO=S△ABC+S△BCO,
∴OA OB=AB CH+OC OB,
∴6×8=10t+6t,
∴t=3,
∴OC=3,
∴C(﹣3,0);
(2)设线BC的表达式为:y=kx+b,
∵B(0,6),C(﹣3,0),
∴直线BC的表达式为:y=2x+6,
设点M(m,2m+6)、N(n,2n+6),
过点M作MF⊥x轴于点F,过点N作NE⊥x轴于点E,
∵△AMN为等腰直角三角形,故AM=AN,
∵∠NAE+∠MAF=90°,∠MAF+∠AMF=90°,
∴∠NAE=∠AMF,
∵∠AFM=∠NEA=90°,AM=AN,
∴△FMA≌△EAN(AAS),
∴EN=AF,MF=AE,
即﹣2n﹣6=m+8,2m+6=8+n,
解得:m=﹣2,n=﹣6,
故点M的坐标为(﹣2,2)、点N(﹣6,﹣6);
由于M,N的位置可能互换,故点N的坐标为(﹣2,2)、点M(﹣6,﹣6);
综上所述,点M的坐标为(﹣2,2)或(﹣6,﹣6);
(3)设点P(0,p),
∴BP2=(p﹣6)2,AP2=82+p2,
①当AB是边时,如图,
∵点A、B、P、Q为顶点的四边形为菱形,
∴BP=AB=10,BP′=AB=10,OB=OP″,
∵B(0,6),
∴P(0,16),P′(0,﹣4),P″(0,﹣6),
∵A(﹣8,0),
∴Q(﹣8,10),Q′(﹣8,﹣10),Q″(8,0);
②当AB是对角线时,如图,
∵点A、B、P、Q为顶点的四边形为菱形,
∴AP=BP,
∴BP2=AP2,
∴(p﹣6)2=82+p2,解得p=﹣,
∴P(0,﹣),
∵A(﹣8,0),B(0,6),
∴Q(﹣8,);
综上所述,点Q的坐标为(﹣8,10)或(﹣8,﹣10)或(8,0)或(﹣8,).
28.解:(1)如图1,∵OC平分∠MON,
∴∠AOD=∠BOD=24°,
∵AB⊥OC,
∴∠ADO=∠BDO=90°,
在△ADO和△BDO中,
,
∴△ADO≌△BDO(ASA),
∴BD=AD,
∵AC∥OB,
∴∠ACO=∠BOD=∠AOC=24°,
∴∠DAC=66°,
在△BDO和△ADC中,
,
∴△BDO≌△ADC(AAS),
同理可证△ADC≌△ADO(AAS),
(2)设∠DCA=x°=∠DAC,
∵AB平分∠OAC,
∴∠DAC=∠DAO=x°,
由题意可得:3x°+24°=180°,
∴x=52,
∴∠OBA=180°﹣48°﹣52°=80°;
(3)当点C在AD的右侧时,∵∠ADC=∠OAB+∠AOD=114°,
∴∠DAC=∠DCA=33°,
∴∠OAC=123°;
当点C在AD的左侧时,
若∠DAC=∠CDA=66°时,∠OAC=90°﹣66°=24°;
若∠DAC=∠DCA时,则∠DAC==57°,
∴∠OAC=33°;
若∠ADC=∠ACD=66°,则∠DAC=48°,
∴∠OAC=42°,
综上所述:∠OAC的度数为123°或24°或33°或42°.
一.选择题(共10小题)
1.“致中和,天地位焉,万物育焉.”对称美是我国古人和谐平衡思想的体现,常被运用于建筑、器物、绘画、标识等作品的设计上,使对称之美惊艳了千年的时光.下面四幅图是我国传统文化与艺术中的几个经典图案,其中不是轴对称图形的是( )
A. B. C. D.
2.已知点P的坐标为(x,y)且,则点P关于原点的对称点P′的坐标是( )
A.(﹣1,) B.(﹣1,) C.(1,) D.(1,)
3.下列各数中,属于无理数的是( )
A. B.0 C. D.
4.关于函数y=﹣x+3的图象,下列结论错误的是( )
A.图象经过一、二、四象限 B.与y轴的交点坐标为(3,0)
C.y随x的增大而减小 D.图象与两坐标轴相交所形成的直角三角形的面积为
5.如图,已知AC=DC,∠1=∠2,如果添加一个条件使△ABC≌△DEC,则添加的条件不可以是( )
A.∠A=∠D B.∠B=∠E C.BC=EC D.AB=DE
6.适合下列条件的△ABC中,直角三角形的个数为( )
①a=32,b=42,c=52;②(c+b)(c﹣b)=a;③∠A+∠B=∠C;④a=1,b=,c=.
A.1个 B.2个 C.3个 D.4
7.如图,△ABC的边长AB=8cm,AC=10cm,BC=4cm,作BC的垂直平分线交AC于D,则△ABD的周长为( )
A.18cm B.14cm C.20cm D.12cm
8.如图,在Rt△ABC中,BE为斜边AC上的中线,点D是AC下方一点,且AD=CD,连接DE,若BE=4,AD=5,则DE的长为( )
A.4.5 B. C.3.5 D.3
9.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;②乙走完全程用了36分钟;
③乙用16分钟追上甲;④乙到达终点时,甲离终点还有300米.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.如图,△ABC中,∠ABC、∠FCA的角平分线BP、CP交于点P,延长BA、BC,PM⊥BE于M,PN⊥BF于N,则下列结论:①AP平分∠EAC;②∠ABC+2∠APC=180°;③∠BAC=2∠BPC;④S△PAC=S△MAP+S△NCP.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题)
11.若有一个数m,它的平方根是a+1和2a﹣7,则m为 .
12.定义:如果一个三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准直角三角形”.如图,将三角形纸片ABC沿着EF折叠,使得点A落在BC边上的点D处,已知∠A=∠B=35°.设∠BED=x°,当△BED和△CDF同时成为“准直角三角形”时,x的值为 .
13.如图,在等腰△ABC中,AB=AC,BE=CD,BD=CF,CG平分∠ACB交DF于点G,∠BED=2∠DFC,若DG=4,BC=17,则BE= .
14.如图,在△ABC中,∠ABC=45°,AB=,AC=6,BC>4,点E,F分别在BC,AC边上,且AF=CE,则AE+BF的最小值为 .
15.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b),则关于x,y的方程组的解是 .
16.如图,直线a⊥直线b于点H,点A、点B是直线上的点,作BC⊥直线b且BC=AB=2cm,作CD⊥直线a于点D,在射线DB上取一点E,使∠AEB=135°,若BH=3cm,则FH= cm.
17.如图,在笔直的公路AB旁有一个城市书房C,C到公路AB的距离CD为80米,AC为100米,BC为300米.一辆公交车以3米/秒的速度从A处向B处缓慢行驶,若公交车鸣笛声会使以公交车为中心170米范围内受到噪音影响,那么公交车至少 秒不鸣笛才能使在城市书房C看书的读者不受鸣笛声影响.
18.如图,在△ABC中,∠ACB=45°,AD⊥BC,BE⊥AC,AD与BE相交于点F,连接并延长CF交AB于点G,∠AEB的平分线交CG的延长线于点H,连接AH,则下列结论:
①∠EBD=45°;②AH=HF;③△ABD≌△CFD;④CH=AB+AH;
⑤BD=CD﹣AF.其中正确的是 .(只填写序号)
三.解答题(共10小题)
19.计算下列各式:
(1)+×(﹣2)2﹣; (2)|﹣|+|﹣2|﹣|﹣1|.
20.已知:2a﹣7和a+1是某正数的两个不相等的平方根,b﹣7的立方根为﹣2.
(1)求a、b的值;
(2)求a﹣b的算术平方根.
21.如图,已知△ABC.
(1)画出与△ABC关于x轴对称的图形△A1B1C1;并写出△A1B1C1各顶点的坐标.
(2)求△ABC的面积.
22.已知y+m与x﹣n成正比例关系.
(1)试说明y是x的一次函数;
(2)若当x=3时,y=3;当x=1时,y=﹣5.求该一次函数的表达式.
23.如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,且BD=BE,CD的垂直平分线MF交AC于F,交BC于M.
(1)求∠ADE的度数;
(2)证明△ADF是等边三角形;
(3)若MF的长为2,求AB的边长.
24.如图所示:∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E.
问:(1)图中有几个等腰三角形?为什么?
(2)BD,CE,DE之间存在着什么关系?请证明.
25.如图,BE是△ABC的角平分线,CD∥AB交BE延长线于点D.
(1)求证:CD=CB.
(2)过A作AF⊥AB交BD于F.若AE=AF,AC=4,BC=5,求AB的长.
26.已知:在△ABC中,D是AB边上的中点,DE⊥DF,垂足为D,DE与AC交于点E,DF与BC交于点F,过点A作AG∥BC与FD的延长线交于点G.
(1)求证:AG=BF;
(2)若EG=5,求EF的长.
27.如图1,直线y=x+6与x,y轴分别交于A,B两点,∠ABO的角平分线与x轴相交于点C.
(1)求点C的坐标;
(2)在直线BC上有两点M,N,△AMN是等腰直角三角形,∠MAN=90°,求点M的坐标;
(3)点P在y轴上,在平面上是否存在点Q,使以点A、B、P、Q为顶点的四边形为菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
28.已知∠MON=48°,点C是∠MON的平分线上一动点,点A,B分别是边ON,OM上动点,AB交OC于点D.
(1)如图1,当AB⊥OC,AC∥OB时,图中有 对全等的三角形,∠DAC= °.
(2)如图2,当AB平分∠OAC,且∠DAC=∠DCA时,求∠OBA的度数.
(3)如图3,当BA⊥ON于点A,在点C移动过程中,△ACD内有两个角相等时,求∠OAC的度数
参考答案
一.选择题(共10小题)
1.D.
2.D.
3.C.
4.B.
5.D.
6.B.
7.A.
8.D.
9.A.
10.D.
二.填空题(共8小题)
11.9.
12.20.
13..
14.2.
15..
16.1.
17.70.
18.①②③④⑤.
三.解答题(共10小题)
19.解:(1)原式=1+×4+4
=1+2+4
=7;
(2)原式=﹣+2﹣﹣(﹣1)
=﹣+2﹣﹣+1
=3﹣2.
20.解:(1)由题意可知:(2a﹣7)+(a+1)=0,
∴3a﹣6=0,
∴a=2,
∵b﹣7的立方根为﹣2
∴b﹣7=(﹣2)3,
∴b=﹣1;
(2)由(1)可知:a=2,b=﹣1,
∴a﹣b=2﹣(﹣1)=3,
∴a+b的算术平方根是.
21.解:(1)如图,△A1B1C1即为所求.
由图可得,A1(3,﹣4),B1(1,﹣2),C1(5,﹣1).
(2)△ABC的面积为=5.
22.解:(1)已知y+m与x﹣n成正比例,
设y+m=k(x﹣n)(k≠0),
y=kx﹣kn﹣m,
因为k≠0,所以y是x的一次函数;
(2)设函数关系式为y=kx+b,
因为x=3时,y=3;x=1时,y=﹣5,
所以,
解得,
所以函数关系式为y=4x﹣9.
23.(1)解:在△ABC中,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
又∵BD=BE,
∴∠BDE=∠BED=×(180°﹣∠B)=75°.
在△ABC中,
∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,
∴∠ADB=90°,
∴∠ADE=∠ADB﹣∠BDE=90°﹣75°=15°;
(2)证明:∵FM垂直平分DC,
∴DF=CF.
∵∠C=30°,
∴∠FDC=∠C=30°,
∴∠AFD=∠C+∠FDC=60°.
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAF=90°﹣∠C=60°,
∴∠AFD=∠DAF=∠ADF=60°,
∴△ADF是等边三角形.
(3)解:∵FM垂直平分DC,
∴∠FMC=90°.
∵∠C=30°,FM=2,
∴FC=2FM=4.
又DF=FC,
∴DF=4.
∵△ADF是等边三角形,
∴AF=DF=4,
∴AC=AF+CF=4+4=8.
又∵AB=AC,
∴AB=8.
24.(1)解:图中有2个等腰三角形即△BDF和△CEF,
理由:∵BF、CF分别平分∠ABC、∠ACB的外角,
∴∠DBF=∠CBF,∠FCE=∠FCG,
∵DE∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCG,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD,EF=CE,
∴△BDF和△CEF为等腰三角形;
(2)存在:BD﹣CE=DE,
证明:∵DF=BD,CE=EF,
∴BD﹣CE=FD﹣EF=DE.
25.(1)证明:∵BE平分∠ABC,
∴∠ABF=∠CBF,
∵CD∥AB,
∴∠ABD=∠D,
∴∠D=∠CBF,
∴CD=CB;
(2)解:∵AF⊥AB,
∴∠FAB=90°,
∴∠AFB+∠ABF=90°,
∵AF=AE,
∴∠AFB=∠AEF,
∵∠AEF=∠CEB,
∴∠AFB=∠CEB,
∵∠ABF=∠CBF,
∴∠CEB+∠CBF=90°,
∴∠ECB=180°﹣(∠CEB+∠CBF)=90°,
在Rt△ABC中,AC=4,BC=5,
∴AB===,
∴AB的长为.
26.(1)证明:∵D是AB边上的中点,
∴AD=BD,
∵AG∥BC,
∴∠GAD=∠B,
在△GAD和△FBD中,
,
∴△GAD≌△FBD(ASA),
∴AG=BF;
(2)解:由(1)可知:△GAD≌△FBD,
∴GD=FD,
∵DE⊥DF,
∴∠EDF=∠EDG=90°,
在△EDG和△EDF中,
,
∴△EDG≌△EDF(SAS),
∴EF=EG=5.
27.解:(1)对于直线y=x+6,令x=0,得到y=6,
∴B(0,6),
令y=0,得到x=﹣8,
∴A(﹣8,0).
∵A(﹣8,0),B(0,6),
∴OA=8,OB=6,
∵∠AOB=90°,
∴AB==10,
过点C作CH⊥AB于H,设OC=t,
∵BC平分∠ABO,∠AOB=90°,
∴CH=OC=t,
∵S△ABO=S△ABC+S△BCO,
∴OA OB=AB CH+OC OB,
∴6×8=10t+6t,
∴t=3,
∴OC=3,
∴C(﹣3,0);
(2)设线BC的表达式为:y=kx+b,
∵B(0,6),C(﹣3,0),
∴直线BC的表达式为:y=2x+6,
设点M(m,2m+6)、N(n,2n+6),
过点M作MF⊥x轴于点F,过点N作NE⊥x轴于点E,
∵△AMN为等腰直角三角形,故AM=AN,
∵∠NAE+∠MAF=90°,∠MAF+∠AMF=90°,
∴∠NAE=∠AMF,
∵∠AFM=∠NEA=90°,AM=AN,
∴△FMA≌△EAN(AAS),
∴EN=AF,MF=AE,
即﹣2n﹣6=m+8,2m+6=8+n,
解得:m=﹣2,n=﹣6,
故点M的坐标为(﹣2,2)、点N(﹣6,﹣6);
由于M,N的位置可能互换,故点N的坐标为(﹣2,2)、点M(﹣6,﹣6);
综上所述,点M的坐标为(﹣2,2)或(﹣6,﹣6);
(3)设点P(0,p),
∴BP2=(p﹣6)2,AP2=82+p2,
①当AB是边时,如图,
∵点A、B、P、Q为顶点的四边形为菱形,
∴BP=AB=10,BP′=AB=10,OB=OP″,
∵B(0,6),
∴P(0,16),P′(0,﹣4),P″(0,﹣6),
∵A(﹣8,0),
∴Q(﹣8,10),Q′(﹣8,﹣10),Q″(8,0);
②当AB是对角线时,如图,
∵点A、B、P、Q为顶点的四边形为菱形,
∴AP=BP,
∴BP2=AP2,
∴(p﹣6)2=82+p2,解得p=﹣,
∴P(0,﹣),
∵A(﹣8,0),B(0,6),
∴Q(﹣8,);
综上所述,点Q的坐标为(﹣8,10)或(﹣8,﹣10)或(8,0)或(﹣8,).
28.解:(1)如图1,∵OC平分∠MON,
∴∠AOD=∠BOD=24°,
∵AB⊥OC,
∴∠ADO=∠BDO=90°,
在△ADO和△BDO中,
,
∴△ADO≌△BDO(ASA),
∴BD=AD,
∵AC∥OB,
∴∠ACO=∠BOD=∠AOC=24°,
∴∠DAC=66°,
在△BDO和△ADC中,
,
∴△BDO≌△ADC(AAS),
同理可证△ADC≌△ADO(AAS),
(2)设∠DCA=x°=∠DAC,
∵AB平分∠OAC,
∴∠DAC=∠DAO=x°,
由题意可得:3x°+24°=180°,
∴x=52,
∴∠OBA=180°﹣48°﹣52°=80°;
(3)当点C在AD的右侧时,∵∠ADC=∠OAB+∠AOD=114°,
∴∠DAC=∠DCA=33°,
∴∠OAC=123°;
当点C在AD的左侧时,
若∠DAC=∠CDA=66°时,∠OAC=90°﹣66°=24°;
若∠DAC=∠DCA时,则∠DAC==57°,
∴∠OAC=33°;
若∠ADC=∠ACD=66°,则∠DAC=48°,
∴∠OAC=42°,
综上所述:∠OAC的度数为123°或24°或33°或42°.
同课章节目录
