2024-2025学年人教版数学八年级上册期末综合练习(第11章~第15章)(含答案)
文档属性
| 名称 | 2024-2025学年人教版数学八年级上册期末综合练习(第11章~第15章)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 428.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 23:12:18 | ||
图片预览

文档简介
2024-2025学年人教版数学八年级上册期末综合练习(第11章~第15章)
一、单选题
1.下列命题中的真命题是( )
A.当时, B.相等的角是对顶角
C. D.若,则
2.如果分式的值为0,那么x的值是( )
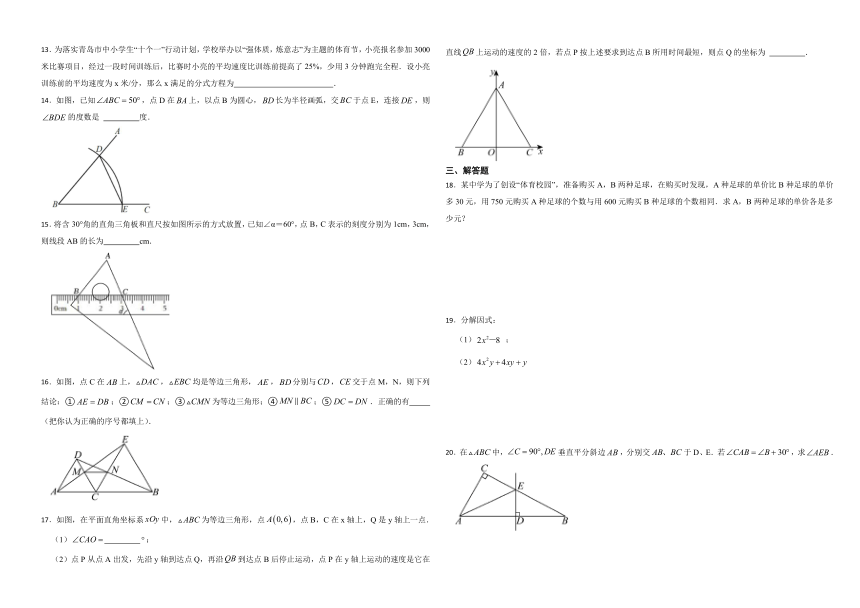
A.1 B. C.2 D.
3.下列各式由左边到右边的变形中,表述正确的是( )
①②
A.都是因式分解
B.都是乘法运算
C.①是因式分解 ②是乘法运算
D.①是乘法运算 ②是因式分解
4.已知多项式分解因式后为,则的值为( )
A.2 B. C.4 D.
5.如图,在中,,若三等分,则图中的等腰三角形有( )
A.4个 B.5个 C.6个 D.7个
6.如图,已知,平分,若,,则的度数是( )
A. B. C. D.
7.A、B两地相距48,一艘轮船从地顺流航行至B地,比从B地逆流航行至地少用,已知水流速度为,求该轮船在静水中的航行速度是多少?若设该轮船在静水中的速度为,则可列方程( )
A. B.
C. D.
8.如图,在平面直角坐标系中,点A的坐标为,点B的坐标为,点P为线段外一动点且,以为边作等边,则当线段的长取到最大值时,点P的横坐标为( )
A.1.5 B.2 C.3 D.1
9.已知,,,则代数式的值为( )
A.4 B.10 C.8 D.6
10.如图,已知△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC.①BD=CE;②∠AHC=60°;③FC=CG;④S△CBD=S△CGH;其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,在中,是的角平分线,,则点到的距离为 .
12.把多项式分解因式的结果是 .
13.为落实青岛市中小学生“十个一”行动计划,学校举办以“强体质,炼意志”为主题的体育节,小亮报名参加3000米比赛项目,经过一段时间训练后,比赛时小亮的平均速度比训练前提高了25%,少用3分钟跑完全程.设小亮训练前的平均速度为x米/分,那么x满足的分式方程为 .
14.如图,已知,点D在上,以点B为圆心,长为半径画弧,交于点E,连接,则的度数是 度.
15.将含30°角的直角三角板和直尺按如图所示的方式放置,已知∠α=60°,点B,C表示的刻度分别为1cm,3cm,则线段AB的长为 cm.
16.如图,点C在上,,均是等边三角形,,分别与,交于点M,N,则下列结论:①;②;③为等边三角形;④;⑤.正确的有 (把你认为正确的序号都填上).
17.如图,在平面直角坐标系中,为等边三角形,点,点B,C在x轴上,Q是y轴上一点.
(1) ;
(2)点P从点A出发,先沿y轴到达点Q,再沿到达点B后停止运动,点P在y轴上运动的速度是它在直线上运动的速度的2倍,若点P按上述要求到达点B所用时间最短,则点Q的坐标为 .
三、解答题
18.某中学为了创设“体育校园”,准备购买A,B两种足球,在购买时发现,A种足球的单价比B种足球的单价多30元,用750元购买A种足球的个数与用600元购买B种足球的个数相同.求A,B两种足球的单价各是多少元?
19.分解因式:
(1) ;
(2)
20.在中,垂直平分斜边,分别交于D、E.若,求.
21.某体育用品商店用4000元购进一批足球,全部售完后,又用3600元再次购进同样的足球,但这次每个足球的进价是第一次进价的1.2倍,且数量比第一次少了10个.
(1)求第一次每个足球的进价是多少元?
(2)若第二次进货后按150元/个的价格销售,当售出10个后,根据市场情况,商店决定对剩余的足球全部按同一标准一次性打折售完,但要求这次的利润不少于450元,问该商店最低可打几折销售?
22.在学习了乘法公式“”的应用后,王老师提出问题:求代数式的最小值.同学们经过探究、合作、交流,最后得到如下的解法:
解:,
∵,∴,
当时,的值最小,最小值为1.
∴的最小值是1,
请你根据上述方法,解答下列问题:
(1)求代数式的最小值;
(2)求代数式的最小值;
(3)若,求的最小值.
23.如图①,在△ABC中,∠ACB=90°,AC=BC,点P是线段AB上的一点,过点A作AE⊥CP,交CP的延长线于点E,过点B作BF⊥CP于点F.
(1)若BF=8,AE=3,则EF=
(2)在图①中,线段AE、BF、EF有怎样的数量关系?请说明理由;
(3)如图②,在△ABC中,∠ACB=90°,AC=BC,点P是△ABC内部的一点,且BP⊥CP,连接AP,若CP=5,求△ACP的面积.
24.某中学为落实《教育部办公厅关于进一步加强中小学生体质健康管理工作的通知》文件要求,决定增设篮球,足球两门选修课程,需要购进一批篮球和足球.若购买篮球的数量是足球的2倍,购买篮球用了6000元,购买足球用了2000元,篮球单价比足球单价贵30元.
(1)求篮球和足球的单价分别是多少元:
(2)学校计划采购篮球、足球共60个,并要求篮球多于40个,且总费用低于4900元.那么有哪几种购买方案?
答案解析部分
1.A
2.C
3.C
4.D
5.C
6.D
7.A
8.A
9.D
10.C
11.4
12.
13.
14.65
15.2
16.①②③④
17.30;
18.购买A种足球单价需要150元,B种足球单价需要120元.
19.(1)2(x+2)(x-2)
(2)
20.
21.(1)100元;(2) 7.5折
22.(1)2
(2)
(3)
23.(1)5
(2)解:BF=EF+AE.
理由如下:∵∠CAE+∠ACE=90°,∠BCF+∠ACE =90°,
∴∠CAE=∠BCF,∵∠E=∠BFC,AC=BC,∴△ACE≌△CBF(AAS) ,
∴AE=CF,CE=BF.
∴CE=EF+CF=EF+AD=BF,即BF=EF+ AE.
(3)解:过点A作AD⊥CP,交CP的延长线于点D,∴∠BPC=∠ADC=∠ACB=90°,
∴∠ACD+BCP=90°=∠ACD+∠CAD.
∴∠CAD=∠BCP.
∵AC=BC,
∴△ACD≌△CBP(AAS).
∴AD=CP=5.
∴S△ACP=×CP×AD =×5×5=
24.(1)解:设足球的单价为x元,则篮球的单价为元,
由题意可得:,
解得,,
经检验是所列方程的根,且符合题意,
此时.
答:篮球的单价为90元,足球的单价为60元;
(2)解:设采购篮球m个,则采购足球为个,
由题意得,,
解得:,
又∵篮球多于40个,
∴,
∵m为整数,
∴m的值可为41,42,43
∴共有三种购买方案,
方案一:采购篮球41个,采购足球19个;
方案二:采购篮球42个,采购足球18个;
方案三:采购篮球43个,采购足球17个.
一、单选题
1.下列命题中的真命题是( )
A.当时, B.相等的角是对顶角
C. D.若,则
2.如果分式的值为0,那么x的值是( )
A.1 B. C.2 D.
3.下列各式由左边到右边的变形中,表述正确的是( )
①②
A.都是因式分解
B.都是乘法运算
C.①是因式分解 ②是乘法运算
D.①是乘法运算 ②是因式分解
4.已知多项式分解因式后为,则的值为( )
A.2 B. C.4 D.
5.如图,在中,,若三等分,则图中的等腰三角形有( )
A.4个 B.5个 C.6个 D.7个
6.如图,已知,平分,若,,则的度数是( )
A. B. C. D.
7.A、B两地相距48,一艘轮船从地顺流航行至B地,比从B地逆流航行至地少用,已知水流速度为,求该轮船在静水中的航行速度是多少?若设该轮船在静水中的速度为,则可列方程( )
A. B.
C. D.
8.如图,在平面直角坐标系中,点A的坐标为,点B的坐标为,点P为线段外一动点且,以为边作等边,则当线段的长取到最大值时,点P的横坐标为( )
A.1.5 B.2 C.3 D.1
9.已知,,,则代数式的值为( )
A.4 B.10 C.8 D.6
10.如图,已知△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC.①BD=CE;②∠AHC=60°;③FC=CG;④S△CBD=S△CGH;其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,在中,是的角平分线,,则点到的距离为 .
12.把多项式分解因式的结果是 .
13.为落实青岛市中小学生“十个一”行动计划,学校举办以“强体质,炼意志”为主题的体育节,小亮报名参加3000米比赛项目,经过一段时间训练后,比赛时小亮的平均速度比训练前提高了25%,少用3分钟跑完全程.设小亮训练前的平均速度为x米/分,那么x满足的分式方程为 .
14.如图,已知,点D在上,以点B为圆心,长为半径画弧,交于点E,连接,则的度数是 度.
15.将含30°角的直角三角板和直尺按如图所示的方式放置,已知∠α=60°,点B,C表示的刻度分别为1cm,3cm,则线段AB的长为 cm.
16.如图,点C在上,,均是等边三角形,,分别与,交于点M,N,则下列结论:①;②;③为等边三角形;④;⑤.正确的有 (把你认为正确的序号都填上).
17.如图,在平面直角坐标系中,为等边三角形,点,点B,C在x轴上,Q是y轴上一点.
(1) ;
(2)点P从点A出发,先沿y轴到达点Q,再沿到达点B后停止运动,点P在y轴上运动的速度是它在直线上运动的速度的2倍,若点P按上述要求到达点B所用时间最短,则点Q的坐标为 .
三、解答题
18.某中学为了创设“体育校园”,准备购买A,B两种足球,在购买时发现,A种足球的单价比B种足球的单价多30元,用750元购买A种足球的个数与用600元购买B种足球的个数相同.求A,B两种足球的单价各是多少元?
19.分解因式:
(1) ;
(2)
20.在中,垂直平分斜边,分别交于D、E.若,求.
21.某体育用品商店用4000元购进一批足球,全部售完后,又用3600元再次购进同样的足球,但这次每个足球的进价是第一次进价的1.2倍,且数量比第一次少了10个.
(1)求第一次每个足球的进价是多少元?
(2)若第二次进货后按150元/个的价格销售,当售出10个后,根据市场情况,商店决定对剩余的足球全部按同一标准一次性打折售完,但要求这次的利润不少于450元,问该商店最低可打几折销售?
22.在学习了乘法公式“”的应用后,王老师提出问题:求代数式的最小值.同学们经过探究、合作、交流,最后得到如下的解法:
解:,
∵,∴,
当时,的值最小,最小值为1.
∴的最小值是1,
请你根据上述方法,解答下列问题:
(1)求代数式的最小值;
(2)求代数式的最小值;
(3)若,求的最小值.
23.如图①,在△ABC中,∠ACB=90°,AC=BC,点P是线段AB上的一点,过点A作AE⊥CP,交CP的延长线于点E,过点B作BF⊥CP于点F.
(1)若BF=8,AE=3,则EF=
(2)在图①中,线段AE、BF、EF有怎样的数量关系?请说明理由;
(3)如图②,在△ABC中,∠ACB=90°,AC=BC,点P是△ABC内部的一点,且BP⊥CP,连接AP,若CP=5,求△ACP的面积.
24.某中学为落实《教育部办公厅关于进一步加强中小学生体质健康管理工作的通知》文件要求,决定增设篮球,足球两门选修课程,需要购进一批篮球和足球.若购买篮球的数量是足球的2倍,购买篮球用了6000元,购买足球用了2000元,篮球单价比足球单价贵30元.
(1)求篮球和足球的单价分别是多少元:
(2)学校计划采购篮球、足球共60个,并要求篮球多于40个,且总费用低于4900元.那么有哪几种购买方案?
答案解析部分
1.A
2.C
3.C
4.D
5.C
6.D
7.A
8.A
9.D
10.C
11.4
12.
13.
14.65
15.2
16.①②③④
17.30;
18.购买A种足球单价需要150元,B种足球单价需要120元.
19.(1)2(x+2)(x-2)
(2)
20.
21.(1)100元;(2) 7.5折
22.(1)2
(2)
(3)
23.(1)5
(2)解:BF=EF+AE.
理由如下:∵∠CAE+∠ACE=90°,∠BCF+∠ACE =90°,
∴∠CAE=∠BCF,∵∠E=∠BFC,AC=BC,∴△ACE≌△CBF(AAS) ,
∴AE=CF,CE=BF.
∴CE=EF+CF=EF+AD=BF,即BF=EF+ AE.
(3)解:过点A作AD⊥CP,交CP的延长线于点D,∴∠BPC=∠ADC=∠ACB=90°,
∴∠ACD+BCP=90°=∠ACD+∠CAD.
∴∠CAD=∠BCP.
∵AC=BC,
∴△ACD≌△CBP(AAS).
∴AD=CP=5.
∴S△ACP=×CP×AD =×5×5=
24.(1)解:设足球的单价为x元,则篮球的单价为元,
由题意可得:,
解得,,
经检验是所列方程的根,且符合题意,
此时.
答:篮球的单价为90元,足球的单价为60元;
(2)解:设采购篮球m个,则采购足球为个,
由题意得,,
解得:,
又∵篮球多于40个,
∴,
∵m为整数,
∴m的值可为41,42,43
∴共有三种购买方案,
方案一:采购篮球41个,采购足球19个;
方案二:采购篮球42个,采购足球18个;
方案三:采购篮球43个,采购足球17个.
同课章节目录
