13.4 课题学习 最短路径问题 同步提优训练(无答案)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 13.4 课题学习 最短路径问题 同步提优训练(无答案)2024-2025学年人教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 264.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-21 00:00:00 | ||
图片预览

文档简介
13.4 课题学习 最短路径问题
基础巩固提优
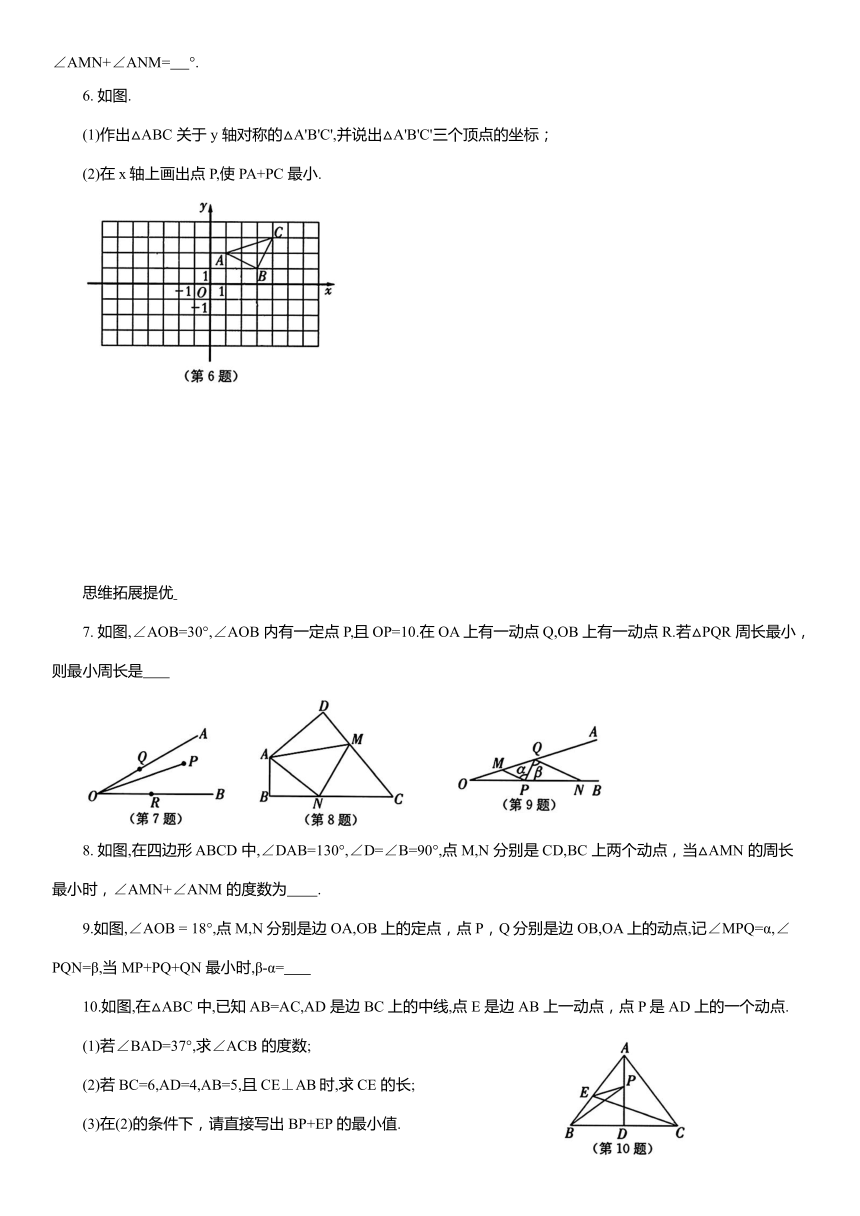
1.如图,河道m的同侧有M,N两个村庄,计划铺设一条管道将河水引至 M,N两地,下面的四个方案中,管道长度最短的是( ).
2.如图,已知∠A=30°,AB=BC,点 D 是射线AE 上的一动点,当BD+CD 最短时,∠ABD 的度数是( ).
A. 110° B. 120° C. 90° D. 80°
3.如图,已知点 D,点 E分别是等边三角形ABC 中 BC,AB 边的中点,AD=6,点 F 是 AD 边上的动点,则 BF+EF 的最小值为( ).
A. 8 B. 6 C. 3 D. 不能确定
4.如图,在△ABC 中,AB=AC,边 AC 的垂直平分线MN 分别交AB,AC 于点M,N,点 D 是边 BC 的中点,点 P是MN 上任意一点,连接 PD,PC,若∠B=α,∠CPD=β,当△PCD 周长取到最小值时,β= (用含α的代数式表示).
5.如图,在四边形 ABCD中,∠BAD=105°,∠B=∠D=90°,在 BC,CD 上分别找一个点M,N,使△AMN 的周长最小,则∠AMN+∠ANM= °.
6. 如图.
(1)作出△ABC 关于 y 轴对称的△A'B'C',并说出△A'B'C'三个顶点的坐标;
(2)在x轴上画出点 P,使 PA+PC 最小.
思维拓展提优
7. 如图,∠AOB=30°,∠AOB 内有一定点 P,且OP=10.在OA 上有一动点Q,OB 上有一动点 R.若△PQR 周长最小,则最小周长是
8. 如图,在四边形 ABCD 中,∠DAB=130°,∠D=∠B=90°,点 M,N 分别是CD,BC 上两个动点,当△AMN 的周长最小时,∠AMN+∠ANM 的度数为 .
9.如图,∠AOB = 18°,点M,N分别是边OA,OB上的定点,点P,Q分别是边OB,OA 上的动点,记∠MPQ=α,∠PQN=β,当 MP+PQ+QN 最小时,β-α=
10.如图,在△ABC 中,已知AB=AC,AD 是边BC 上的中线,点E 是边AB 上一动点,点P 是AD 上的一个动点.
(1)若∠BAD=37°,求∠ACB 的度数;
(2)若BC=6,AD=4,AB=5,且CE⊥AB时,求CE 的长;
(3)在(2)的条件下,请直接写出BP+EP 的最小值.
11.如图,△ABC 是等边三角形,D 为 BC 边上一个动点(D 与 B,C均不重合). AD=AE.∠DAE=60°,连接CE.
(1)求证:CE平分∠ACF;
(2)若AB=2,当四边形 ADCE 的周长取最小值时,求BD 的长.
延伸探究提优
12. 如图,在△ABC 中,AB=AC,∠A=45°,E是AC上的一点, 过点C作CD⊥AB 于点D,交 BE 于点 P.
(1)直接写出图中除△ABC 外的所有等腰三角形;
(2)求证:
(3)点 H,G 分别为边 AC,BC 上的动点,当△DHG 周长取最小值时,求∠HDG 的度数.
基础巩固提优
1.如图,河道m的同侧有M,N两个村庄,计划铺设一条管道将河水引至 M,N两地,下面的四个方案中,管道长度最短的是( ).
2.如图,已知∠A=30°,AB=BC,点 D 是射线AE 上的一动点,当BD+CD 最短时,∠ABD 的度数是( ).
A. 110° B. 120° C. 90° D. 80°
3.如图,已知点 D,点 E分别是等边三角形ABC 中 BC,AB 边的中点,AD=6,点 F 是 AD 边上的动点,则 BF+EF 的最小值为( ).
A. 8 B. 6 C. 3 D. 不能确定
4.如图,在△ABC 中,AB=AC,边 AC 的垂直平分线MN 分别交AB,AC 于点M,N,点 D 是边 BC 的中点,点 P是MN 上任意一点,连接 PD,PC,若∠B=α,∠CPD=β,当△PCD 周长取到最小值时,β= (用含α的代数式表示).
5.如图,在四边形 ABCD中,∠BAD=105°,∠B=∠D=90°,在 BC,CD 上分别找一个点M,N,使△AMN 的周长最小,则∠AMN+∠ANM= °.
6. 如图.
(1)作出△ABC 关于 y 轴对称的△A'B'C',并说出△A'B'C'三个顶点的坐标;
(2)在x轴上画出点 P,使 PA+PC 最小.
思维拓展提优
7. 如图,∠AOB=30°,∠AOB 内有一定点 P,且OP=10.在OA 上有一动点Q,OB 上有一动点 R.若△PQR 周长最小,则最小周长是
8. 如图,在四边形 ABCD 中,∠DAB=130°,∠D=∠B=90°,点 M,N 分别是CD,BC 上两个动点,当△AMN 的周长最小时,∠AMN+∠ANM 的度数为 .
9.如图,∠AOB = 18°,点M,N分别是边OA,OB上的定点,点P,Q分别是边OB,OA 上的动点,记∠MPQ=α,∠PQN=β,当 MP+PQ+QN 最小时,β-α=
10.如图,在△ABC 中,已知AB=AC,AD 是边BC 上的中线,点E 是边AB 上一动点,点P 是AD 上的一个动点.
(1)若∠BAD=37°,求∠ACB 的度数;
(2)若BC=6,AD=4,AB=5,且CE⊥AB时,求CE 的长;
(3)在(2)的条件下,请直接写出BP+EP 的最小值.
11.如图,△ABC 是等边三角形,D 为 BC 边上一个动点(D 与 B,C均不重合). AD=AE.∠DAE=60°,连接CE.
(1)求证:CE平分∠ACF;
(2)若AB=2,当四边形 ADCE 的周长取最小值时,求BD 的长.
延伸探究提优
12. 如图,在△ABC 中,AB=AC,∠A=45°,E是AC上的一点, 过点C作CD⊥AB 于点D,交 BE 于点 P.
(1)直接写出图中除△ABC 外的所有等腰三角形;
(2)求证:
(3)点 H,G 分别为边 AC,BC 上的动点,当△DHG 周长取最小值时,求∠HDG 的度数.
