第三章 二次函数 单元测试(含答案)2024-2025学年鲁教版(五四制)(2012)九年级数学 上册
文档属性
| 名称 | 第三章 二次函数 单元测试(含答案)2024-2025学年鲁教版(五四制)(2012)九年级数学 上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 379.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-21 00:00:00 | ||
图片预览



文档简介
第三章《二次函数》单元测试
2024-2025学年九年级上册数学鲁教版(五四制)(2012)
一、单选题
1.对于点,,定义一种运算:.例如,,,.若互不重合的四点,满足,则四点( )
A.在同一条直线上 B.在同一条抛物线上
C.在同一反比例函数图象上 D.是同一个正方形的四个顶点
2.若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
A.≤m<1 B.<m≤1 C.1<m≤2 D.1<m<2
3.如图,在平面直角坐标系中,抛物线y=﹣x2+2x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+AP的最小值为( ).
A. B. C.3 D.2
4.根据抛物线与x轴的交点的坐标,可以求出下列方程中哪个方程的近似解( )
A. B.
C. D.
5.抛物线的部分图象如图所示,当时,则的取值范围是( )
A. B. C.或 D.或
6.将抛物线向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为( )
A. B.
C. D.
7.平行于x轴的直线与抛物线的一个交点坐标为(-1,2),则另一个交点坐标为( )
A.(1,2) B.(1,-2) C.(5,2) D.(-1,4)
8.设二次函数(a,c为实数,)的图象过点,,,,则( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
9.已知二次函数的图象如图所示,令,则( )
A.M>0 B.M<0
C.M=0 D.M的符号不能确定
10.二次函数的图象如图所示,则下列关系式中错误的是.
A. B. C. D.
二、填空题
11.如图,已知抛物线与轴相交于点,与轴交于点.点在平面直角坐标系第一象限内的抛物线上运动,设的面积为.下列结论:①;②;③,其中正确结论的序号是 .(所有正确的序号都填上)
12.一个二次函数的图象顶点坐标为(4,3),形状与开口方向和抛物线相同,这个函数解析式为
13.已知抛物线的对称轴为,与轴的一个交点为,若关于的一元二次方程有整数根,则的值有 个.
14.将抛物线向上平移4个单位长度,向右平移2个单位后,所得抛物线的解析式是 .
15.若x=﹣m和x=m﹣4时,多项式ax2+bx+4a+1的值相等,且m≠2.当﹣1<x<2时,存在x的值,使多项式ax2+bx+4a+1的值为3,则a的取值范围是 .
16.把二次函数的图象先向右平移1个单位长度,再向下平移3个单位长度,得到的新抛物线的顶点坐标是 .
17.如下图,抛物线与x轴交于点下列判断:①;②;③;④.其中判断一定正确的序号是 .
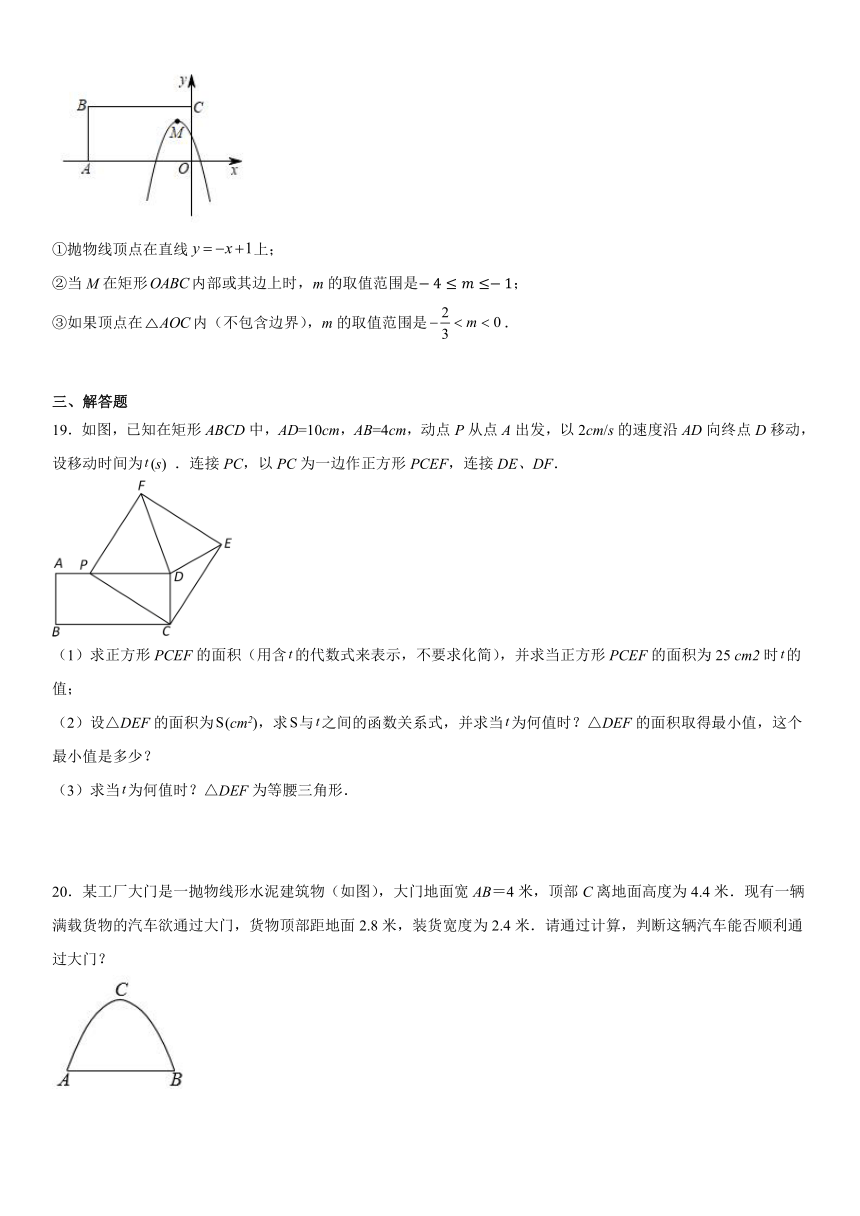
18.如图,矩形中,,抛物线的顶点为M,下列说法正确的结论有 .
①抛物线顶点在直线上;
②当M在矩形内部或其边上时,m的取值范围是;
③如果顶点在内(不包含边界),m的取值范围是.
三、解答题
19.如图,已知在矩形ABCD中,AD=10cm,AB=4cm,动点P从点A出发,以2cm/s的速度沿AD向终点D移动,设移动时间为(s) .连接PC,以PC为一边作正方形PCEF,连接DE、DF.
(1)求正方形PCEF的面积(用含的代数式来表示,不要求化简),并求当正方形PCEF的面积为25 cm2时的值;
(2)设△DEF的面积为(cm2),求与之间的函数关系式,并求当为何值时?△DEF的面积取得最小值,这个最小值是多少?
(3)求当为何值时?△DEF为等腰三角形.
20.某工厂大门是一抛物线形水泥建筑物(如图),大门地面宽AB=4米,顶部C离地面高度为4.4米.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8米,装货宽度为2.4米.请通过计算,判断这辆汽车能否顺利通过大门?
21.如图,抛物线过点.
(1)求抛物线的解析式;
(2)设点P是直线上方抛物线上一点,求出的最大面积及此时点P的坐标.
22.已知抛物线y=﹣x2﹣2x+3.问:
(1)该抛物线的顶点坐标是 ;
(2)该函数与x轴的交点坐标是 , ,并在网格中画出该函数的图象;
(3)x取什么值时,抛物线在x轴上方? .
(4)已知y=t,t取什么值时与抛物线y=﹣x2﹣2x+3有两个交点?
23.某公司投入研发费用40万元(40万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为4元/件.此产品年销售量y(万件)与售价x(元件)之间满足函数关系式y=﹣x+20.
(1)求这种产品第一年的利润W(万元)与售价x(元件)满足的函数关系式;
(2)该产品第一年的利润为24万元,那么该产品第一年的售价是多少?
(3)第二年,该公司将第一年的利润24万元(24万元只计入第二年成本)再次投入研发,使产品的生产成本降为3元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过10万件.请计算该公司第二年的利润W2至少为多少万元.
24.如图,在平面直角坐标系中,直线分别交x轴、y轴于点A、点B,交双曲线于点抛物线过点B,且与该双曲线交于点D,点D的纵坐标为.
(1)求双曲线与抛物线的解析式.
(2)若点P为该抛物线上一点,点Q为该双曲线上一点,且P,Q两点的纵坐标都为,求线段的长.
(3)若点M沿直线从点A运动到点C,再沿双曲线从点C运动到点D.过点M作轴,交抛物线于点N.设线段的长度为d,点M的横坐标为m,直接写出d的最大值,以及d随m的增大而减小时m的取值范围.
参考答案:
1.A
2.B
3.C
4.A
5.A
6.D
7.C
8.C
9.B
10.C
11.①②
12.
13.3
14.
15.
16.
17.①②/②①
18.①③/③①
19.(1)当=3.5s时,正方形PCEF的面积为25cm2;(2)当s时,取得最小值为6;(3)当s,3 s或4 s时,△DEF为等腰三角形.
20.这辆汽车正好可以通过大门.
21.(1)
(2),
22.(1)顶点坐标为(﹣1,4);(2)抛物线与x轴的交点坐标为(﹣3,0),(1,0);(3)当﹣3<x<1时,y>0,抛物线在x轴上方;(4)当t<4时,直线y=t与抛物线y=﹣x2﹣2x+3有两个交点.
23.;12元; 46万元.
24.(1),;(2)或;(3)的最大值是,,,时,随的增大而减小.
2024-2025学年九年级上册数学鲁教版(五四制)(2012)
一、单选题
1.对于点,,定义一种运算:.例如,,,.若互不重合的四点,满足,则四点( )
A.在同一条直线上 B.在同一条抛物线上
C.在同一反比例函数图象上 D.是同一个正方形的四个顶点
2.若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
A.≤m<1 B.<m≤1 C.1<m≤2 D.1<m<2
3.如图,在平面直角坐标系中,抛物线y=﹣x2+2x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+AP的最小值为( ).
A. B. C.3 D.2
4.根据抛物线与x轴的交点的坐标,可以求出下列方程中哪个方程的近似解( )
A. B.
C. D.
5.抛物线的部分图象如图所示,当时,则的取值范围是( )
A. B. C.或 D.或
6.将抛物线向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为( )
A. B.
C. D.
7.平行于x轴的直线与抛物线的一个交点坐标为(-1,2),则另一个交点坐标为( )
A.(1,2) B.(1,-2) C.(5,2) D.(-1,4)
8.设二次函数(a,c为实数,)的图象过点,,,,则( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
9.已知二次函数的图象如图所示,令,则( )
A.M>0 B.M<0
C.M=0 D.M的符号不能确定
10.二次函数的图象如图所示,则下列关系式中错误的是.
A. B. C. D.
二、填空题
11.如图,已知抛物线与轴相交于点,与轴交于点.点在平面直角坐标系第一象限内的抛物线上运动,设的面积为.下列结论:①;②;③,其中正确结论的序号是 .(所有正确的序号都填上)
12.一个二次函数的图象顶点坐标为(4,3),形状与开口方向和抛物线相同,这个函数解析式为
13.已知抛物线的对称轴为,与轴的一个交点为,若关于的一元二次方程有整数根,则的值有 个.
14.将抛物线向上平移4个单位长度,向右平移2个单位后,所得抛物线的解析式是 .
15.若x=﹣m和x=m﹣4时,多项式ax2+bx+4a+1的值相等,且m≠2.当﹣1<x<2时,存在x的值,使多项式ax2+bx+4a+1的值为3,则a的取值范围是 .
16.把二次函数的图象先向右平移1个单位长度,再向下平移3个单位长度,得到的新抛物线的顶点坐标是 .
17.如下图,抛物线与x轴交于点下列判断:①;②;③;④.其中判断一定正确的序号是 .
18.如图,矩形中,,抛物线的顶点为M,下列说法正确的结论有 .
①抛物线顶点在直线上;
②当M在矩形内部或其边上时,m的取值范围是;
③如果顶点在内(不包含边界),m的取值范围是.
三、解答题
19.如图,已知在矩形ABCD中,AD=10cm,AB=4cm,动点P从点A出发,以2cm/s的速度沿AD向终点D移动,设移动时间为(s) .连接PC,以PC为一边作正方形PCEF,连接DE、DF.
(1)求正方形PCEF的面积(用含的代数式来表示,不要求化简),并求当正方形PCEF的面积为25 cm2时的值;
(2)设△DEF的面积为(cm2),求与之间的函数关系式,并求当为何值时?△DEF的面积取得最小值,这个最小值是多少?
(3)求当为何值时?△DEF为等腰三角形.
20.某工厂大门是一抛物线形水泥建筑物(如图),大门地面宽AB=4米,顶部C离地面高度为4.4米.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8米,装货宽度为2.4米.请通过计算,判断这辆汽车能否顺利通过大门?
21.如图,抛物线过点.
(1)求抛物线的解析式;
(2)设点P是直线上方抛物线上一点,求出的最大面积及此时点P的坐标.
22.已知抛物线y=﹣x2﹣2x+3.问:
(1)该抛物线的顶点坐标是 ;
(2)该函数与x轴的交点坐标是 , ,并在网格中画出该函数的图象;
(3)x取什么值时,抛物线在x轴上方? .
(4)已知y=t,t取什么值时与抛物线y=﹣x2﹣2x+3有两个交点?
23.某公司投入研发费用40万元(40万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为4元/件.此产品年销售量y(万件)与售价x(元件)之间满足函数关系式y=﹣x+20.
(1)求这种产品第一年的利润W(万元)与售价x(元件)满足的函数关系式;
(2)该产品第一年的利润为24万元,那么该产品第一年的售价是多少?
(3)第二年,该公司将第一年的利润24万元(24万元只计入第二年成本)再次投入研发,使产品的生产成本降为3元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过10万件.请计算该公司第二年的利润W2至少为多少万元.
24.如图,在平面直角坐标系中,直线分别交x轴、y轴于点A、点B,交双曲线于点抛物线过点B,且与该双曲线交于点D,点D的纵坐标为.
(1)求双曲线与抛物线的解析式.
(2)若点P为该抛物线上一点,点Q为该双曲线上一点,且P,Q两点的纵坐标都为,求线段的长.
(3)若点M沿直线从点A运动到点C,再沿双曲线从点C运动到点D.过点M作轴,交抛物线于点N.设线段的长度为d,点M的横坐标为m,直接写出d的最大值,以及d随m的增大而减小时m的取值范围.
参考答案:
1.A
2.B
3.C
4.A
5.A
6.D
7.C
8.C
9.B
10.C
11.①②
12.
13.3
14.
15.
16.
17.①②/②①
18.①③/③①
19.(1)当=3.5s时,正方形PCEF的面积为25cm2;(2)当s时,取得最小值为6;(3)当s,3 s或4 s时,△DEF为等腰三角形.
20.这辆汽车正好可以通过大门.
21.(1)
(2),
22.(1)顶点坐标为(﹣1,4);(2)抛物线与x轴的交点坐标为(﹣3,0),(1,0);(3)当﹣3<x<1时,y>0,抛物线在x轴上方;(4)当t<4时,直线y=t与抛物线y=﹣x2﹣2x+3有两个交点.
23.;12元; 46万元.
24.(1),;(2)或;(3)的最大值是,,,时,随的增大而减小.
