四川省遂宁市射洪市2024-2025学年八年级上学期11月期中数学试题(无答案)
文档属性
| 名称 | 四川省遂宁市射洪市2024-2025学年八年级上学期11月期中数学试题(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 304.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 00:00:00 | ||
图片预览



文档简介
2024年初2023级半期考试
数学学科试题
试卷满分:150分 考试时间:120分钟
一、选择题(每小题3分,共60分)
1.下列说法中,正确的是( )
A. B.的算术平方根是3
C.1的立方根是 D.是7的一个平方根
2.在,,,,,,(相邻两个1之间0的个数逐次加1)中,无理数的个数有( )
A.4个 B.3个 C.2个 D.1个
3. 要使成立,则a的取值范围是( )
A. B. C. D. 一切实数
4. 已知,则的算术平方根是( )
A. B. C. ±2 D. 2
5.若一个正数x的平方根是2a﹣1和﹣a+2,则这个正数x为( )
A.﹣1 B.-3 C.9 D. 9或
6.实数a、b、c在数轴上的位置如图:
则化简的结果是( )
A.a-b-c B.a-b+c C.-a+b+c D.-a+b-c
7.下列运算正确的是( )
A. B.
C. D.
8.已知,则( )
A.17 B.24 C.36 D.72
9.若与的乘积中不含x的一次项,则a的值是( )
A. B.0 C.3 D.9
10.的计算结果是( )
A. B.3 C. D.-3
11.观察下列图形由左到右的变化,写出相应的代数恒等式为( ).
A . B.
C . D.
12.下列各式从左到右的变形中,是因式分解的是( )
A. B.
C. D.
13. 下列各式中不能用平方差公式计算的是( )
A. B.
C. D.
14.如果是一个完全平方式,那么m的值是( )
A.7 B.- 7 C.- 5或7 D.- 5或5
15.下列语句中,是命题的是( )
A.延长线段到 B.两点之间线段最短
C.画 D.等角的余角相等吗?
16.在下列条件中,不能说明△ABC≌△A′B′C′的是( )
A.∠A=∠A′,∠C=∠C′,AC=A′C′
B.∠A=∠A′,AB=A′B′,BC=B′C′
C.∠B=∠B′,∠C=∠C′,AB=A′B′
D.AB=A′B′, BC=B′C,AC=A′C′
17.如图,,要使≌,需要补充
的一个条件是( )
A. B.
C. D.
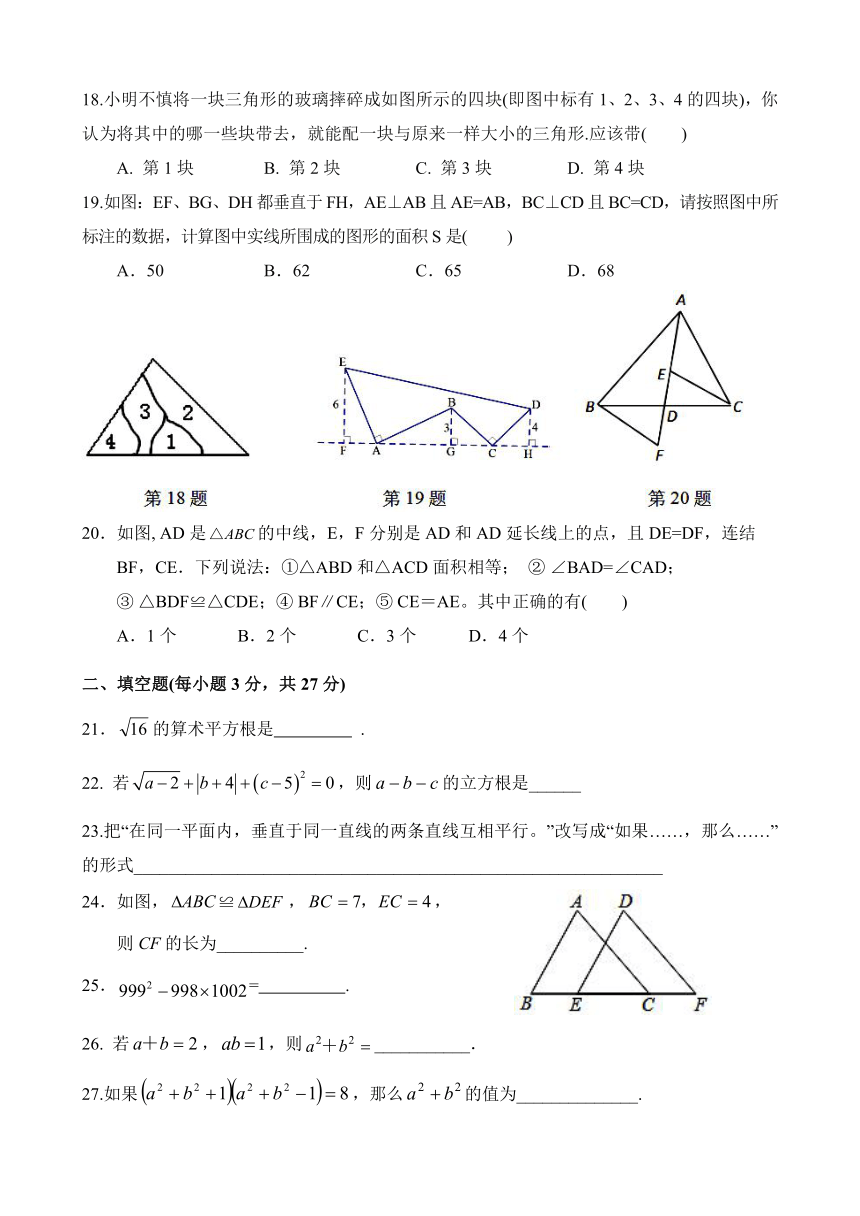
18.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形.应该带( )
A. 第1块 B. 第2块 C. 第3块 D. 第4块
19.如图:EF、BG、DH都垂直于FH,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
A.50 B.62 C.65 D.68
20.如图, AD是的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结
BF,CE.下列说法:①△ABD和△ACD面积相等; ② ∠BAD=∠CAD;
③ △BDF≌△CDE;④ BF∥CE;⑤ CE=AE。其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共27分)
21.的算术平方根是 .
22. 若,则的立方根是______
23.把“在同一平面内,垂直于同一直线的两条直线互相平行。”改写成“如果……,那么……”的形式_____________________________________________________________
24.如图,≌,,
则CF的长为__________.
25.= .
26. 若,,则___________.
27.如果,那么的值为______________.
28.已知是的三边的长,且满足,此三角形的形状是______________.
29.下面是一个按某种规律排列的数阵:
根据数阵排列的规律,第n(n为整数且n≥3)行从左向右数第(n﹣2)个数是 (用含n的代数式表示).
三、计算或化简(每小题5分,共10分)
30. 计算:
(1)
四、分解因式(每小题5分,共20分)
31. 分解因式:
(1)2x-8 (2)
(3) (4)
五、解答题:(共33分)
32. (6分)先化简再求值:[(-x+2y)(-x-2y)-(x+4y)2]÷(-4y),其中x=5,y=2
33. (6分)已知的立方根是,的算术平方根是,是的整数部分.
(1)求a,b,c的值;
(2)求的平方根
34.(6分)如图,在中,的延长线于点,,
(1)求证:
(2)判断这三条线段之间的数量关系,并说明理由。
35.(7分) 如图,在中,D为上一点,E为中点,连接并延长至点F,使得,连.
(1)求证:
(2)若,连接平分,平分,求的度数.
36.(8分)教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式.
原式;
例如:求代数式的最小值.
原式.可知当时,有最小值,最小值是-8.
(1)分解因式:______.
(2)试说明:x、y取任何实数时,多项式的值总为正数.
(3)当m,n为何值时,多项式有最小值,并求出这个最小值.
数学学科试题
试卷满分:150分 考试时间:120分钟
一、选择题(每小题3分,共60分)
1.下列说法中,正确的是( )
A. B.的算术平方根是3
C.1的立方根是 D.是7的一个平方根
2.在,,,,,,(相邻两个1之间0的个数逐次加1)中,无理数的个数有( )
A.4个 B.3个 C.2个 D.1个
3. 要使成立,则a的取值范围是( )
A. B. C. D. 一切实数
4. 已知,则的算术平方根是( )
A. B. C. ±2 D. 2
5.若一个正数x的平方根是2a﹣1和﹣a+2,则这个正数x为( )
A.﹣1 B.-3 C.9 D. 9或
6.实数a、b、c在数轴上的位置如图:
则化简的结果是( )
A.a-b-c B.a-b+c C.-a+b+c D.-a+b-c
7.下列运算正确的是( )
A. B.
C. D.
8.已知,则( )
A.17 B.24 C.36 D.72
9.若与的乘积中不含x的一次项,则a的值是( )
A. B.0 C.3 D.9
10.的计算结果是( )
A. B.3 C. D.-3
11.观察下列图形由左到右的变化,写出相应的代数恒等式为( ).
A . B.
C . D.
12.下列各式从左到右的变形中,是因式分解的是( )
A. B.
C. D.
13. 下列各式中不能用平方差公式计算的是( )
A. B.
C. D.
14.如果是一个完全平方式,那么m的值是( )
A.7 B.- 7 C.- 5或7 D.- 5或5
15.下列语句中,是命题的是( )
A.延长线段到 B.两点之间线段最短
C.画 D.等角的余角相等吗?
16.在下列条件中,不能说明△ABC≌△A′B′C′的是( )
A.∠A=∠A′,∠C=∠C′,AC=A′C′
B.∠A=∠A′,AB=A′B′,BC=B′C′
C.∠B=∠B′,∠C=∠C′,AB=A′B′
D.AB=A′B′, BC=B′C,AC=A′C′
17.如图,,要使≌,需要补充
的一个条件是( )
A. B.
C. D.
18.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形.应该带( )
A. 第1块 B. 第2块 C. 第3块 D. 第4块
19.如图:EF、BG、DH都垂直于FH,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
A.50 B.62 C.65 D.68
20.如图, AD是的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结
BF,CE.下列说法:①△ABD和△ACD面积相等; ② ∠BAD=∠CAD;
③ △BDF≌△CDE;④ BF∥CE;⑤ CE=AE。其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共27分)
21.的算术平方根是 .
22. 若,则的立方根是______
23.把“在同一平面内,垂直于同一直线的两条直线互相平行。”改写成“如果……,那么……”的形式_____________________________________________________________
24.如图,≌,,
则CF的长为__________.
25.= .
26. 若,,则___________.
27.如果,那么的值为______________.
28.已知是的三边的长,且满足,此三角形的形状是______________.
29.下面是一个按某种规律排列的数阵:
根据数阵排列的规律,第n(n为整数且n≥3)行从左向右数第(n﹣2)个数是 (用含n的代数式表示).
三、计算或化简(每小题5分,共10分)
30. 计算:
(1)
四、分解因式(每小题5分,共20分)
31. 分解因式:
(1)2x-8 (2)
(3) (4)
五、解答题:(共33分)
32. (6分)先化简再求值:[(-x+2y)(-x-2y)-(x+4y)2]÷(-4y),其中x=5,y=2
33. (6分)已知的立方根是,的算术平方根是,是的整数部分.
(1)求a,b,c的值;
(2)求的平方根
34.(6分)如图,在中,的延长线于点,,
(1)求证:
(2)判断这三条线段之间的数量关系,并说明理由。
35.(7分) 如图,在中,D为上一点,E为中点,连接并延长至点F,使得,连.
(1)求证:
(2)若,连接平分,平分,求的度数.
36.(8分)教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式.
原式;
例如:求代数式的最小值.
原式.可知当时,有最小值,最小值是-8.
(1)分解因式:______.
(2)试说明:x、y取任何实数时,多项式的值总为正数.
(3)当m,n为何值时,多项式有最小值,并求出这个最小值.
同课章节目录
