湘教版数学八年级上册期末复习题二(精华 含答案)
文档属性
| 名称 | 湘教版数学八年级上册期末复习题二(精华 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 268.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-19 21:30:17 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版数学八年级上册期末复习题二(精华)
一、填空题
1.请将命题“平行于同一直线的两直线互相平行”改成“如果,那么”的形式: .
2.已知,若,,,则的长是 .
3.将一组数据,,,,,,,按下面的方法进行排列:
,,,,;
,,,,,
,
若的位置记为,的位置记为,则这组数中最大的数的位置记为 .
4.如图,根据机器零件的设计图纸,用不等式表示零件长度L的合格尺寸(L的取值范围) .
5.已知关于x的方程的解是正数,则m的取值范围为 .
6.如图,在中,,,点D为边上一动点(不与点B、C重合),垂直交于点E,垂足为点H,连接并延长交于点F.①若是边上的中线,则 ;②若平分,则 .
二、单选题
7.如图,中,,,,则的度数为( )
[ERRORIMAGE:http://tikupic.21cnjy.com/ct20241o/bd/1c/bd1c5f4bc5d16013dcf2b6c5a392bddb.jpg]
A. B. C. D.
8.在实数:,,,中,最小的数是( )
A. B. C. D.
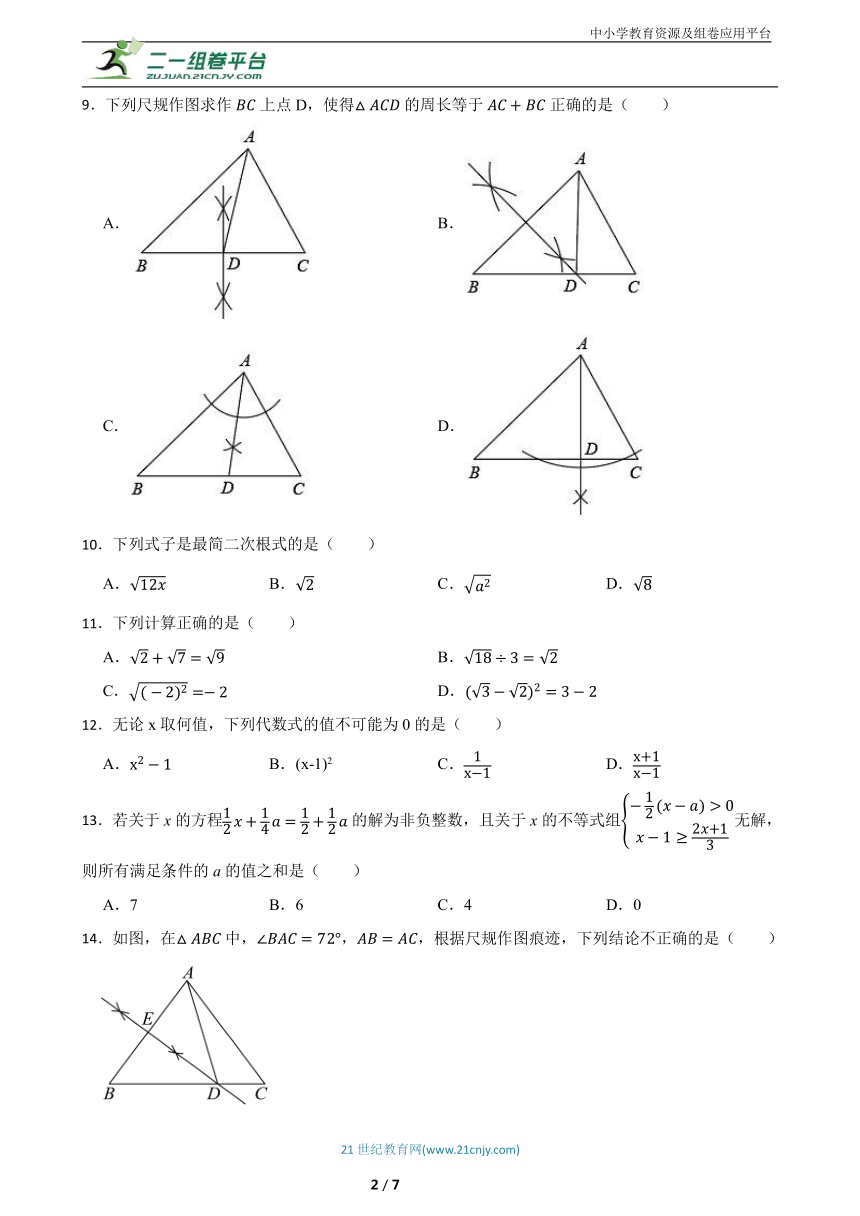
9.下列尺规作图求作上点D,使得的周长等于正确的是( )
A. B.
C. D.
10.下列式子是最简二次根式的是( )
A. B. C. D.
11.下列计算正确的是( )
A. B.
C. D.
12.无论x取何值,下列代数式的值不可能为0的是( )
A. B.(x-1)2 C. D.
13.若关于x的方程的解为非负整数,且关于x的不等式组无解,则所有满足条件的a的值之和是( )
A.7 B.6 C.4 D.0
14.如图,在中,,,根据尺规作图痕迹,下列结论不正确的是( )
A. B.
C. D.
15.如图,AB=AD,点B关于AC的对称点E恰好落在CD上.若∠BAD=α(0°<a<180°),∠ACB=β,则下列关系正确的是( )
A.a﹣β=90° B.α+β=180°
C.c=3β D.a+2β=180°
16.如图,在和中,,,,,连接,,延长交于点F,连接.下列结论:①;②;③;④平分.其中正确的结论个数有( )个.
A.4 B.3 C.2 D.1
三、解答题
17.把下列实数表示在数轴上,并比较它们的大小(用“<”连接).
18.解方程:.
19.按要求化简、求值或解方程.
(1),为实数,且满足,求的算术平方根;
(2)先化简,再求值:,其中
(3)解方程:
20.在一次研究性学习中,同学们对乘法公式进行了研究.
(1)如图,大正方形的边长为(a+b),请直接写出下列结果.
①中间小正方形的边长;
②用含a,b的等式表示大正方形面积与小正方形面积的差等于图中一个长方形面积的4倍.
(2)当x+y=6,x-y=-4时,求xy的值.
(3)若当x-2y=P,xy=Q时,(x+2y)的值唯一确定,用含P的代数式表示Q.
四、计算题
21.计算
(1)
(2)
22.计算: .
23.先化简,再求值:,其中.
答案解析部分
1.【答案】两条直线都平行于同一条直线,那么这两条直线互相平行
【知识点】平行公理及推论;定义、命题、定理、推论的概念
2.【答案】
【知识点】三角形全等及其性质
3.【答案】
【知识点】二次根式的性质与化简;探索数与式的规律
4.【答案】
【知识点】一元一次不等式组的应用
5.【答案】且
【知识点】解分式方程;解一元一次不等式
6.【答案】;
【知识点】三角形的角平分线、中线和高;三角形的面积;角平分线的性质;相似三角形的判定与性质;等腰直角三角形
7.【答案】B
【知识点】三角形内角和定理;三角形的外角性质;等腰三角形的性质
8.【答案】B
【知识点】无理数的估值;零指数幂
9.【答案】B
【知识点】线段垂直平分线的性质;尺规作图-作角的平分线;尺规作图-垂直平分线
10.【答案】B
【知识点】最简二次根式
11.【答案】B
【知识点】二次根式的性质与化简;二次根式的乘除法;二次根式的加减法
12.【答案】C
【知识点】分式的值为零的条件;偶次方的非负性
13.【答案】C
【知识点】一元一次方程的解;解一元一次方程;一元一次不等式组的特殊解;一元一次不等式组的含参问题
14.【答案】C
【知识点】线段垂直平分线的性质;等腰三角形的性质;尺规作图-垂直平分线
15.【答案】D
【知识点】三角形内角和定理;三角形的外角性质;等腰三角形的性质-等边对等角
16.【答案】B
【知识点】三角形内角和定理;三角形全等及其性质;三角形全等的判定
17.【答案】解:,
将下列实数在数轴上表示如下:
用“”连接为:,
故答案为:.
【知识点】无理数在数轴上表示;无理数的大小比较
18.【答案】x=﹣2
【知识点】解分式方程
19.【答案】(1)
(2),
(3)或
【知识点】分式的化简求值;二次根式有意义的条件;因式分解法解一元二次方程;求算术平方根
20.【答案】(1)解:①由拼图可知:中间小正方形的边长为a-b;
②大正方形的面积为(a+b)2,小正方形的面积为(a-b)2,每个小长方形的长为a,宽为b,则小长方形的面积为ab;
∴(a+b)2-(a-b)2=4ab,即大正方形面积与小正方形面积的差等于图中一个长方形面积的4倍;
(2)当x+y=6,x-y=-4时,
∵(x+y)2-(x-y)2=4xy,
∴62-(-4)2=4xy,即xy=5;
(3)由(1)得:(x+2y)2-(x-2y)2=8xy,
而 x-2y=P,xy=Q,
∴(x+2y)2-P2=8Q,即(x+2y)2=P2+8Q.
【知识点】完全平方公式及运用;平方差公式及应用;求代数式的值-整体代入求值
21.【答案】(1)
(2)
【知识点】分式的乘除法;分式的加减法
22.【答案】解:原式
=1﹣1+2+2
=4.
【知识点】实数的运算
23.【答案】解:原式
,
当时,原式.
【知识点】分式的混合运算;分式的化简求值
21世纪教育网(www.21cnjy.com)
2 / 7
湘教版数学八年级上册期末复习题二(精华)
一、填空题
1.请将命题“平行于同一直线的两直线互相平行”改成“如果,那么”的形式: .
2.已知,若,,,则的长是 .
3.将一组数据,,,,,,,按下面的方法进行排列:
,,,,;
,,,,,
,
若的位置记为,的位置记为,则这组数中最大的数的位置记为 .
4.如图,根据机器零件的设计图纸,用不等式表示零件长度L的合格尺寸(L的取值范围) .
5.已知关于x的方程的解是正数,则m的取值范围为 .
6.如图,在中,,,点D为边上一动点(不与点B、C重合),垂直交于点E,垂足为点H,连接并延长交于点F.①若是边上的中线,则 ;②若平分,则 .
二、单选题
7.如图,中,,,,则的度数为( )
[ERRORIMAGE:http://tikupic.21cnjy.com/ct20241o/bd/1c/bd1c5f4bc5d16013dcf2b6c5a392bddb.jpg]
A. B. C. D.
8.在实数:,,,中,最小的数是( )
A. B. C. D.
9.下列尺规作图求作上点D,使得的周长等于正确的是( )
A. B.
C. D.
10.下列式子是最简二次根式的是( )
A. B. C. D.
11.下列计算正确的是( )
A. B.
C. D.
12.无论x取何值,下列代数式的值不可能为0的是( )
A. B.(x-1)2 C. D.
13.若关于x的方程的解为非负整数,且关于x的不等式组无解,则所有满足条件的a的值之和是( )
A.7 B.6 C.4 D.0
14.如图,在中,,,根据尺规作图痕迹,下列结论不正确的是( )
A. B.
C. D.
15.如图,AB=AD,点B关于AC的对称点E恰好落在CD上.若∠BAD=α(0°<a<180°),∠ACB=β,则下列关系正确的是( )
A.a﹣β=90° B.α+β=180°
C.c=3β D.a+2β=180°
16.如图,在和中,,,,,连接,,延长交于点F,连接.下列结论:①;②;③;④平分.其中正确的结论个数有( )个.
A.4 B.3 C.2 D.1
三、解答题
17.把下列实数表示在数轴上,并比较它们的大小(用“<”连接).
18.解方程:.
19.按要求化简、求值或解方程.
(1),为实数,且满足,求的算术平方根;
(2)先化简,再求值:,其中
(3)解方程:
20.在一次研究性学习中,同学们对乘法公式进行了研究.
(1)如图,大正方形的边长为(a+b),请直接写出下列结果.
①中间小正方形的边长;
②用含a,b的等式表示大正方形面积与小正方形面积的差等于图中一个长方形面积的4倍.
(2)当x+y=6,x-y=-4时,求xy的值.
(3)若当x-2y=P,xy=Q时,(x+2y)的值唯一确定,用含P的代数式表示Q.
四、计算题
21.计算
(1)
(2)
22.计算: .
23.先化简,再求值:,其中.
答案解析部分
1.【答案】两条直线都平行于同一条直线,那么这两条直线互相平行
【知识点】平行公理及推论;定义、命题、定理、推论的概念
2.【答案】
【知识点】三角形全等及其性质
3.【答案】
【知识点】二次根式的性质与化简;探索数与式的规律
4.【答案】
【知识点】一元一次不等式组的应用
5.【答案】且
【知识点】解分式方程;解一元一次不等式
6.【答案】;
【知识点】三角形的角平分线、中线和高;三角形的面积;角平分线的性质;相似三角形的判定与性质;等腰直角三角形
7.【答案】B
【知识点】三角形内角和定理;三角形的外角性质;等腰三角形的性质
8.【答案】B
【知识点】无理数的估值;零指数幂
9.【答案】B
【知识点】线段垂直平分线的性质;尺规作图-作角的平分线;尺规作图-垂直平分线
10.【答案】B
【知识点】最简二次根式
11.【答案】B
【知识点】二次根式的性质与化简;二次根式的乘除法;二次根式的加减法
12.【答案】C
【知识点】分式的值为零的条件;偶次方的非负性
13.【答案】C
【知识点】一元一次方程的解;解一元一次方程;一元一次不等式组的特殊解;一元一次不等式组的含参问题
14.【答案】C
【知识点】线段垂直平分线的性质;等腰三角形的性质;尺规作图-垂直平分线
15.【答案】D
【知识点】三角形内角和定理;三角形的外角性质;等腰三角形的性质-等边对等角
16.【答案】B
【知识点】三角形内角和定理;三角形全等及其性质;三角形全等的判定
17.【答案】解:,
将下列实数在数轴上表示如下:
用“”连接为:,
故答案为:.
【知识点】无理数在数轴上表示;无理数的大小比较
18.【答案】x=﹣2
【知识点】解分式方程
19.【答案】(1)
(2),
(3)或
【知识点】分式的化简求值;二次根式有意义的条件;因式分解法解一元二次方程;求算术平方根
20.【答案】(1)解:①由拼图可知:中间小正方形的边长为a-b;
②大正方形的面积为(a+b)2,小正方形的面积为(a-b)2,每个小长方形的长为a,宽为b,则小长方形的面积为ab;
∴(a+b)2-(a-b)2=4ab,即大正方形面积与小正方形面积的差等于图中一个长方形面积的4倍;
(2)当x+y=6,x-y=-4时,
∵(x+y)2-(x-y)2=4xy,
∴62-(-4)2=4xy,即xy=5;
(3)由(1)得:(x+2y)2-(x-2y)2=8xy,
而 x-2y=P,xy=Q,
∴(x+2y)2-P2=8Q,即(x+2y)2=P2+8Q.
【知识点】完全平方公式及运用;平方差公式及应用;求代数式的值-整体代入求值
21.【答案】(1)
(2)
【知识点】分式的乘除法;分式的加减法
22.【答案】解:原式
=1﹣1+2+2
=4.
【知识点】实数的运算
23.【答案】解:原式
,
当时,原式.
【知识点】分式的混合运算;分式的化简求值
21世纪教育网(www.21cnjy.com)
2 / 7
同课章节目录
