北师大版数学八年级(上)期末检测题(无答案)
文档属性
| 名称 | 北师大版数学八年级(上)期末检测题(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-21 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师版数学八年级(上)期末检测题
A卷(共100分)
一、选择题(每小题只有一个正确答案,每小题4分,共32分)
1.9的平方根是( )
A.81 B.±3 C.3 D.-3
2.函数y=中,自变量x的取值范围是( )
A.x>3 B.x<3 C.x≥3 D.x≠3
3.下列命题是真命题的是( )
A.任何实数都有平方根. B.若a2=b2,则a=b.
C.-8的立方根是-2 D.
4.下列四组数据不能作为直角三角形三边的是( )
A. B.3,4,6 C. 6,8,10 D.5,12,13
5.对于函数y=-3x+1,下列结论正确的是( )
A.它的图解必经过点(-1,3) B. 它的图解经过第一、二、三象限
C.y的值随x值的增大而增大 D.当x=时,y=0
6.如图,已知正方形ABCD的边长为2,如果将对角线BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么AD′的长为( )
A. B. C. D.
第6题图 第7题图
7.如图所示的象棋盘上,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”所在点的坐标是 ( )
A.(1,-2) B.(-2,1) C.(-2,2) D.(2,-2)
8.某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,如图,l1、l2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则以下判断错误的是( )
A、骑车的同学比步行的同学晚出发30分钟
B、步行的速度是6千米/时
C、骑车的同学从出发到追上步行同学用了20分钟
D、骑车的同学和步行的同学同时到达目的地
二、填空题(每小题4分,共20分)
9.满足的整数x是 。
10.已知是方程2x-ay=3的一个解,那么a的值是 。
11.有两名学员甲和乙一起练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计甲和乙两人中的新手是 .他们成绩的方差大小关系是S甲2 S乙2(填“∠”、“>”或”“=”).
12.一次函数的图象与直线y=x+1平行,且过点(1,3),一次函数的解析式为 。
13.表1、表2分别给出了两条直线l1:y=k1x+b1与l2:y=k2x+b2上部分点的横坐标x和纵坐标y的对应值.
表1
表2
则方程组的解为 。 第13题图
三、解答下列各题(共48分)
14.计算下列各题(每小题5分,共15分)
(1) (2)
(3)解方程组
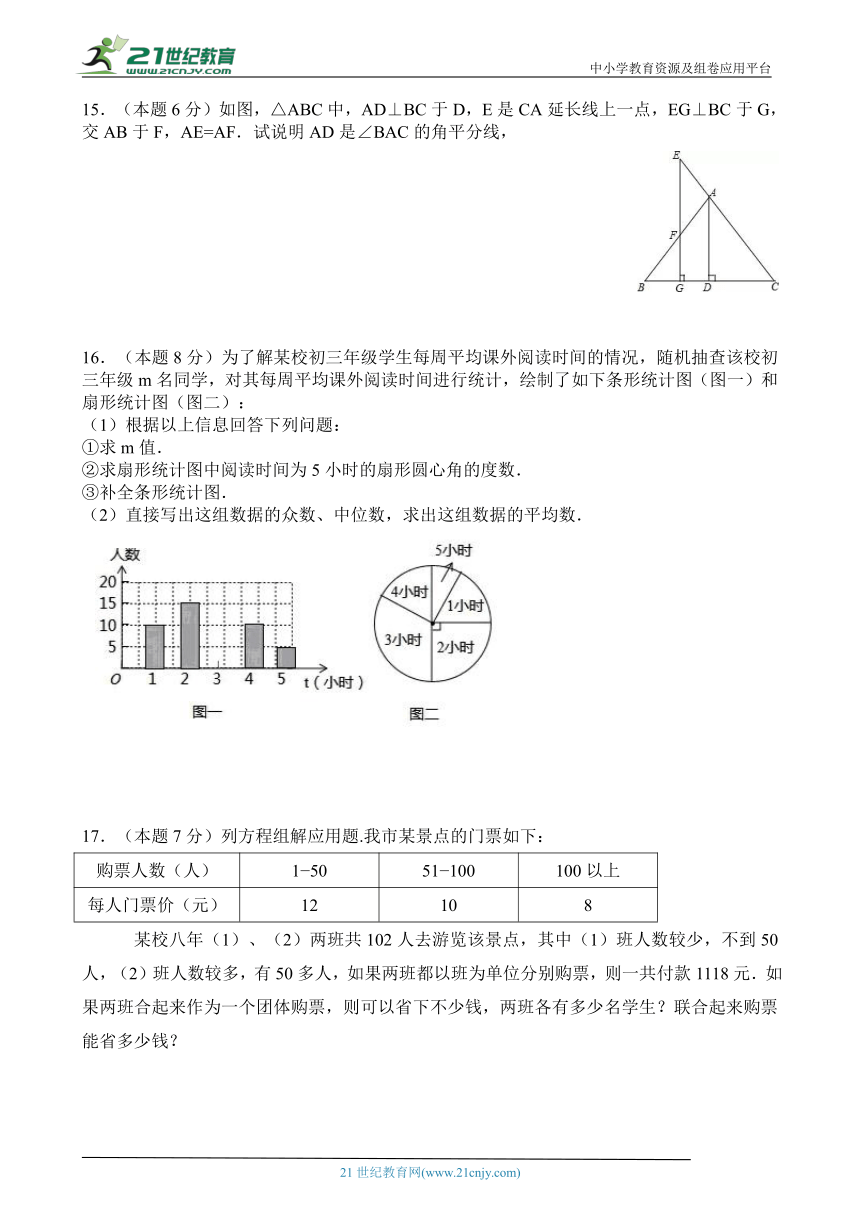
15.(本题6分)如图,△ABC中,AD⊥BC于D,E是CA延长线上一点,EG⊥BC于G,交AB于F,AE=AF.试说明AD是∠BAC的角平分线,
16.(本题8分)为了解某校初三年级学生每周平均课外阅读时间的情况,随机抽查该校初三年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
17.(本题7分)列方程组解应用题.我市某景点的门票如下:
购票人数(人) 1 50 51 100 100以上
每人门票价(元) 12 10 8
某校八年(1)、(2)两班共102人去游览该景点,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人,如果两班都以班为单位分别购票,则一共付款1118元.如果两班合起来作为一个团体购票,则可以省下不少钱,两班各有多少名学生?联合起来购票能省多少钱?
18.(本题12分)如图,直线l1的函数表达式为:y= 3x+3,且l1与x轴交于点D,直线l2表达式为:y=kx+b且经过点A、B,直线l1、l2交于点C.
(1)求直线l2函数表达式和点C的坐标.直接写出使得函数y=kx+b 的值大于函数y= 3x+3的值的自变量x的取值范围。
(2)如果点P在直线l2上,满足△ADP的面积是△ADC面积的两倍,请求出P点坐标;
(3)在y轴上是否存在点Q,使得四边形QDBC周长最小?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
B卷(共50分)
一、填空题(每小题4分,共20分)
19.如果,则2y-x的平方根是 。
20.实数a,b,c在数轴上的位置如图所示,
化简代数式的值: 。
21.如图△ABC中,∠A=60°,BD⊥AC于D,CE⊥AB于E,BD、CE相交于点F,∠FBC、∠FCB的平分线交于点O,则∠BOC的度数为 。
22.某二元一次方程的解是(m为常数).若把x看做平面直角坐标系中一个点P的横坐标,y看做点P的纵坐标,下列5种说法中正确的是 (写出序号)
①点P(x,y)一定不在第三象限;
②点P(x,y)可能是坐标原点;
③点P(x,y)的纵坐标y随横坐标x增大而增大;
④点P(x,y)的纵坐标y随横坐标x增大而减小.
⑤横坐标x的值每增加1,纵坐标y的值会减少3。
23.如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数的图象上,从左向右第3个正方形中的一个顶点A的坐标为(12,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是 ,S3的值为 .
二、解答题(共30分
24.(本题8分)如图,某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.
(1)直接写出y与x之间的函数关系式;
(2)分别求出第10天和第15天的销售金额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
25.(本题10分)如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P、D分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.
(1)本题证明的思路可用下列框图表示:
根据上述思路,请你完整地书写本题的证明过程.
(2)若PB平分∠ABO,其余条件不变.求证:AP=CD.
(3)若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)
26.(本题12分)如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图2,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师版数学八年级(上)期末检测题
A卷(共100分)
一、选择题(每小题只有一个正确答案,每小题4分,共32分)
1.9的平方根是( )
A.81 B.±3 C.3 D.-3
2.函数y=中,自变量x的取值范围是( )
A.x>3 B.x<3 C.x≥3 D.x≠3
3.下列命题是真命题的是( )
A.任何实数都有平方根. B.若a2=b2,则a=b.
C.-8的立方根是-2 D.
4.下列四组数据不能作为直角三角形三边的是( )
A. B.3,4,6 C. 6,8,10 D.5,12,13
5.对于函数y=-3x+1,下列结论正确的是( )
A.它的图解必经过点(-1,3) B. 它的图解经过第一、二、三象限
C.y的值随x值的增大而增大 D.当x=时,y=0
6.如图,已知正方形ABCD的边长为2,如果将对角线BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么AD′的长为( )
A. B. C. D.
第6题图 第7题图
7.如图所示的象棋盘上,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”所在点的坐标是 ( )
A.(1,-2) B.(-2,1) C.(-2,2) D.(2,-2)
8.某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,如图,l1、l2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则以下判断错误的是( )
A、骑车的同学比步行的同学晚出发30分钟
B、步行的速度是6千米/时
C、骑车的同学从出发到追上步行同学用了20分钟
D、骑车的同学和步行的同学同时到达目的地
二、填空题(每小题4分,共20分)
9.满足的整数x是 。
10.已知是方程2x-ay=3的一个解,那么a的值是 。
11.有两名学员甲和乙一起练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计甲和乙两人中的新手是 .他们成绩的方差大小关系是S甲2 S乙2(填“∠”、“>”或”“=”).
12.一次函数的图象与直线y=x+1平行,且过点(1,3),一次函数的解析式为 。
13.表1、表2分别给出了两条直线l1:y=k1x+b1与l2:y=k2x+b2上部分点的横坐标x和纵坐标y的对应值.
表1
表2
则方程组的解为 。 第13题图
三、解答下列各题(共48分)
14.计算下列各题(每小题5分,共15分)
(1) (2)
(3)解方程组
15.(本题6分)如图,△ABC中,AD⊥BC于D,E是CA延长线上一点,EG⊥BC于G,交AB于F,AE=AF.试说明AD是∠BAC的角平分线,
16.(本题8分)为了解某校初三年级学生每周平均课外阅读时间的情况,随机抽查该校初三年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
17.(本题7分)列方程组解应用题.我市某景点的门票如下:
购票人数(人) 1 50 51 100 100以上
每人门票价(元) 12 10 8
某校八年(1)、(2)两班共102人去游览该景点,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人,如果两班都以班为单位分别购票,则一共付款1118元.如果两班合起来作为一个团体购票,则可以省下不少钱,两班各有多少名学生?联合起来购票能省多少钱?
18.(本题12分)如图,直线l1的函数表达式为:y= 3x+3,且l1与x轴交于点D,直线l2表达式为:y=kx+b且经过点A、B,直线l1、l2交于点C.
(1)求直线l2函数表达式和点C的坐标.直接写出使得函数y=kx+b 的值大于函数y= 3x+3的值的自变量x的取值范围。
(2)如果点P在直线l2上,满足△ADP的面积是△ADC面积的两倍,请求出P点坐标;
(3)在y轴上是否存在点Q,使得四边形QDBC周长最小?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
B卷(共50分)
一、填空题(每小题4分,共20分)
19.如果,则2y-x的平方根是 。
20.实数a,b,c在数轴上的位置如图所示,
化简代数式的值: 。
21.如图△ABC中,∠A=60°,BD⊥AC于D,CE⊥AB于E,BD、CE相交于点F,∠FBC、∠FCB的平分线交于点O,则∠BOC的度数为 。
22.某二元一次方程的解是(m为常数).若把x看做平面直角坐标系中一个点P的横坐标,y看做点P的纵坐标,下列5种说法中正确的是 (写出序号)
①点P(x,y)一定不在第三象限;
②点P(x,y)可能是坐标原点;
③点P(x,y)的纵坐标y随横坐标x增大而增大;
④点P(x,y)的纵坐标y随横坐标x增大而减小.
⑤横坐标x的值每增加1,纵坐标y的值会减少3。
23.如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数的图象上,从左向右第3个正方形中的一个顶点A的坐标为(12,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是 ,S3的值为 .
二、解答题(共30分
24.(本题8分)如图,某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.
(1)直接写出y与x之间的函数关系式;
(2)分别求出第10天和第15天的销售金额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
25.(本题10分)如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P、D分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.
(1)本题证明的思路可用下列框图表示:
根据上述思路,请你完整地书写本题的证明过程.
(2)若PB平分∠ABO,其余条件不变.求证:AP=CD.
(3)若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)
26.(本题12分)如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图2,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
