实数（一）

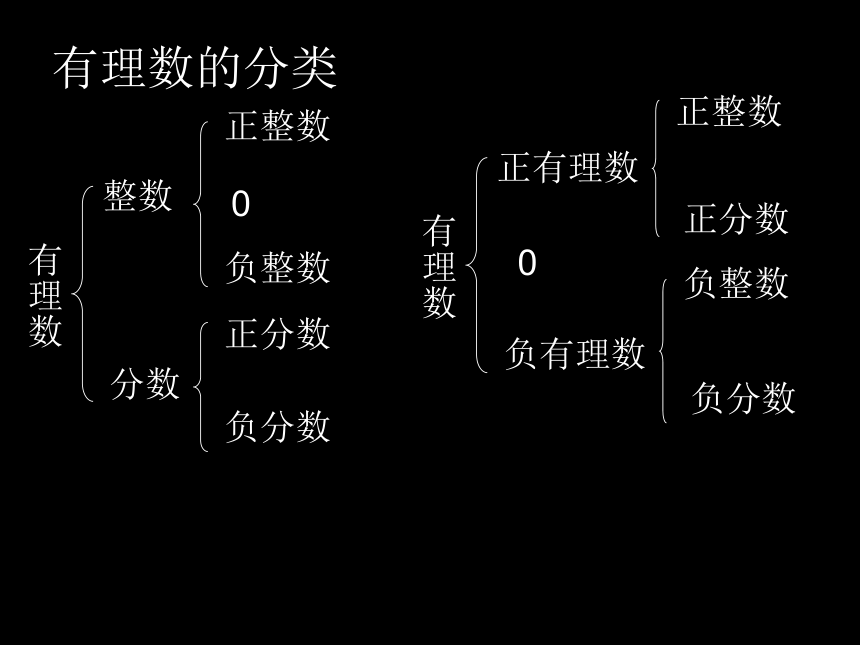
课件17张PPT。13.3 实数（一）初二（15）班 朱 健 铭 以前学过？110+210－1－ 52 122.5－7.5一、引入，下列的数你会把它们归类吗？1、在以上各数中, 是我们以前学过的有理数吗?110，+21，0， 122.5，－52，－1， －7.5，2、什么是有理数?有理数可以分哪几类?数提示有理数的分类有理数有理数负分数负整数二、探究使用计数器计算,把下列各数写成小数的形式，你有什么发现？二、探究使用计数器计算,把下列各数写成小数的形式，你有什么发现？1、任何一个有理数都可写成有限小数或无限循环小数的形式。2、任何有限小数或无限循环小数也都是有理数。除了有限小数和无限循环小数，还有什么其它类型的小数吗？三、思考无限不循环小数——无理数你能举出一些无理数吗？2.开不尽的方根３.有规律但不循环
的无限小数1. 及含 的数1、下列各数中是无理数的是（ ）
A、－1.414 B、3.14 C、 D、
2、判断正误
①有理数都是有限小数 （ ）
②有限小数都是有理数 （ ）
③无理数都是无限小数 （ ）
④无限小数都是无理数 （ ）
⑤带根号的数都是无理数 （ ）
⑥不带根号的数都是有理数 （ ）练习C××××√√练习：完成《同步练习》P39.课堂导学.#2。方法：1、先找 类
2、找含根号的数
3、找不循环小数
4、有理数四、实数的分类实数有理数无理数整数分数可化成有限小数
或无限循环小数可化成无限不循环小数实数练习1、《同步练习》P39.课堂精练。
提示：带根号的都是无理数吗？
是无理数还是有理数？
2、 《同步练习》P40.A组.#2。五、探究1、每一个有理数都可用数轴上的一个点表示，
每一个无理数能否用数轴上的一个点表示？
2、你能在数轴上找到表示 、 、 这样的
无理数的点吗？归纳1、每一个有理数都可用数轴上的一个点表示，每一个无理数都可用数轴上的一个点表示。2、数轴上的点有些表示有理数，有些表示无理数。3、实数与数轴上的点一一对应。1、如图，数轴上点P表示的数可能是（ ）
A、 B、 C、 D、-3.22、如下图，数轴上表示 的点是（ ）练习CB3、课本P86.练习.#1六、小结1、什么是无理数？
2、实数的分类？
3、实数与数轴上的点的关系？七、作业1、课本P86.习题#1、2；练习#1；
2、《同步练习》P40.A组.