北师大版数学八年级下册 第二章 一元一次不等式和一元一次不等式组 综合测试卷(含答案)
文档属性
| 名称 | 北师大版数学八年级下册 第二章 一元一次不等式和一元一次不等式组 综合测试卷(含答案) | 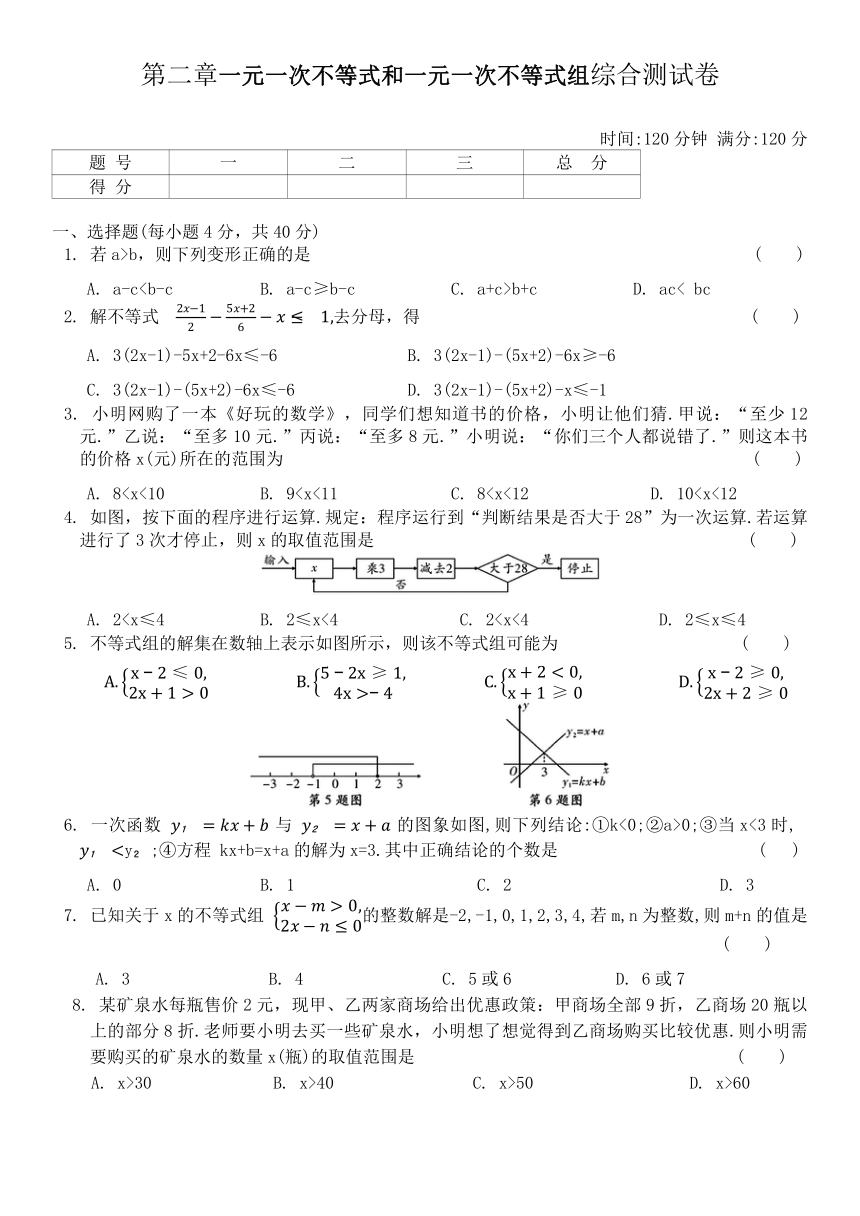 | |
| 格式 | docx | ||
| 文件大小 | 364.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-21 22:21:50 | ||
图片预览



文档简介
第二章一元一次不等式和一元一次不等式组综合测试卷
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 若a>b,则下列变形正确的是 ( )
A. a-cb+c D. ac< bc
2. 解不等式 去分母,得 ( )
A. 3(2x-1)-5x+2-6x≤-6 B. 3(2x-1)-(5x+2)-6x≥-6
C. 3(2x-1)-(5x+2)-6x≤-6 D. 3(2x-1)-(5x+2)-x≤-1
3. 小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少12元.”乙说:“至多10元.”丙说:“至多8元.”小明说:“你们三个人都说错了.”则这本书的价格x(元)所在的范围为 ( )
A. 84. 如图,按下面的程序进行运算.规定:程序运行到“判断结果是否大于28”为一次运算.若运算进行了3次才停止,则x的取值范围是 ( )
A. 25. 不等式组的解集在数轴上表示如图所示,则该不等式组可能为 ( )
6. 一次函数 与 的图象如图,则下列结论:①k<0;②a>0;③当x<3时, y ;④方程 kx+b=x+a的解为x=3.其中正确结论的个数是 ( )
A. 0 B. 1 C. 2 D. 3
7. 已知关于x的不等式组 的整数解是-2,-1,0,1,2,3,4,若m,n为整数,则m+n的值是 ( )
A. 3 B. 4 C. 5或6 D. 6或7
8. 某矿泉水每瓶售价2元,现甲、乙两家商场给出优惠政策:甲商场全部9折,乙商场20瓶以上的部分8折.老师要小明去买一些矿泉水,小明想了想觉得到乙商场购买比较优惠.则小明需要购买的矿泉水的数量x(瓶)的取值范围是 ( )
A. x>30 B. x>40 C. x>50 D. x>60
9. 如图所示是按某影视厅放映电影的盈利y(元)与售出票数x(张)之间的函数关系画出的图象.要使放映一场电影的盈利不少于300 元,最少应卖出电影票的张数为 ( )
A. 85 B. 86
C. 84 D. 83
10. 我们定义例如: 若x满足 则x的整数解有 ( )
A. 0个 B. 1个 C. 2个 D. 3个
二、填空题(每小题3分,共18分)
11. 不等式2x-1≤4的最大整数解是 .
12. 已知关于x,y的方程组 的解满足不等式组则满足条件的m的整数值为 .
13. 已知实数x,y满足2x-3y=4,且x>-1,y≤2,设k=x-y,则k的取值范围是 .
14. 已知一次函数 和 ,当自变量x> -1时, ,则k的取值范围为
15. 对于三个数a,b,c,我们给出符号来表示其中最大(小)的数,规定 min{a,b,c}表示这三个数中最小的数, max{a,b,c}表示这三个数中最大的数.例如: min{-1,2,3} = - 1, max{-1,2,3}=3;若 min{4,x+4,4-x}= max{2,x+1,2x},则x的值为 .
16. 重庆一中初二年级老师为同学们购买《老人与海》、《泰戈尔诗集》和《雨的四季》供大家借阅,已知三种书单价之和为120元,计划购买三种书数量总共不超过125本,其中《老人与海》单价为50元,计划购买25本,《泰戈尔诗集》至少购买15本,《雨的四季》数量不少于《泰戈尔诗集》的2倍,在做预算时将《雨的四季》和《泰戈尔诗集》的单价弄反了,结果实际购买三种书的总价比预算多了116元,若三本书的单价均为整数,则实际购买这三种书最多需要花费 元.
三、解答题(共62分)
17. (8分)解不等式(组),并将解集在数轴上表示出来:
18. (8分)已知关于x的不等式
(1)若 是该不等式的解,求a的取值范围.
(2)在(1)的条件下,且: 不是该不等式的解,求符合题意的一个无理数a.
19. (10分)已知关于x的不等式组
(1)如果这个不等式组无解,求k的取值范围.
(2)如果这个不等式组有解,求k的取值范围.
(3)如果这个不等式组恰好有2 017个整数解,求k的取值范围.
20. (6分)请阅读求绝对值不等式 和 的解集的过程.
对于绝对值不等式 ,从图1 的数轴上看:大于 而小于3 的数的绝对值小于3,所以 的解集为
对于绝对值不等式 ,从图2的数轴上看:小于 而大于3的数的绝对值大于3,所以 的解集为 或
已知关于x,y的二元一次方程组 的解满足 ,其中m是负整数,求m的值.
21. (9分)已知直线 的图象经过点 ,且与直线 交于点
B(1,b).
(1)求直线 的表达式,并直接写出不等式 的解集.
(2)若O为坐标原点,直线 与x轴交于点 C,在x轴上是否存在一点 P,满足 若存在,求出此时点 P 的坐标;若不存在,请说明理由.
22. (10分)对于不等式: 且 当 时, 当 时, ,请根据以上信息,解答以下问题:
(1)解关于x的不等式:
(2)若关于x的不等式: 且 在 上存在x的值使其成立,求k的取值范围.
23. (11分)在今年的新冠疫情期间,政府紧急组织一批物资送往武汉.现已知这批物资中,食品和矿泉水共410箱,且食品比矿泉水多110箱.
(1)求食品和矿泉水各有多少箱
(2)现计划租用A,B两种货车共10辆,一次性将所有物资送到群众手中,已知A种货车最多可装食品40箱和矿泉水10箱,B种货车最多可装食品20箱和矿泉水20箱,试通过计算帮助政府设计出几种运输方案.
(3)在(2)条件下,A种货车每辆需付运费600元,B种货车每辆需付运费450元,政府应该选择哪种方案,才能使运费最少 最少运费是多少
第二章一元一次不等式和一元一次不等式组综合测试卷
C2. C3. D4. A5. B6. C7. C8. B9. C 10. B11. 212. - 2或-3 13. 1且 或-2 16. 4 808
17. 解:(1)去分母,得x-5+2>2x-6,解得x<3,在数轴上表示出来为:
②解不等式①,得x≤1,
解不等式②,得x>-2,故不等式组的解集为-218. 解:(1)把x=2代入(x-5)( ax-3a+4)≤0,得(2-5)(2a-3a+4)≤0,解得a≤4.
(2)∵x=1不是该不等式的解,∴当x=1时,(x-5)( ax-3a+4)>0,即(1-5)(a-3a+4)>0,解得a>2,由(1)得a≤4,
∴满足x=1不是该不等式的解的无理数a可以是π.
19. 解:(1)根据题意,得-1≥1-k,解得k≥2.
(2)根据题意,得-1<1-k,解得k<2.
(3)∵不等式组恰好有2017个整数解,∴ - 120. 解:∵|x+y|≤3,∴ - 3≤x+y≤3,由
②
得3x+3y= -3m-3,∴x+y= -m-1,
则-3≤-m-1≤3,解得-4≤m≤2,又∵m是负整数,
∴m的值为-4或-3或-2或-1.
21. 解:(1)由题意得两直线交点横坐标为1.
由图象知不等式 的解集为x≤1.
(2)存在.当y=0时,即-x+4=0,解得x=4,则C(4,0),设P(t,0),
解得t=10或t= - 2,∴P 点坐标为(-2,0),(10,0).
22. 解: ∴2x>2,解得x>1.
(2)由题意得,当a>1时,x-k<5x-2,解得 -1,解得k>6.
当05x-2,解得 解得
23. 解:(1)设食品有x箱,矿泉水有y箱,依题意,
得:解得
即:食品有260箱,矿泉水有150箱.
(2)设租用A种货车m辆,则租用B种货车( 辆,
依题意,得: 解得:
又∵m为正整数,∴m可以为3,4,5,
∴共有3种运输方案,方案1:租用A种货车3 辆,B种货车7辆;
方案2:租用A种货车4辆,B种货车6辆;
方案3:租用A种货车5辆,B种货车5辆.
(3)选择方案1所需运费为 (元),选择方案2所需运费为 (元),选择方案3所需运费为 (元).
∴政府应该选择方案1,才能使运费最少,最少运费是4950元.
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 若a>b,则下列变形正确的是 ( )
A. a-c
2. 解不等式 去分母,得 ( )
A. 3(2x-1)-5x+2-6x≤-6 B. 3(2x-1)-(5x+2)-6x≥-6
C. 3(2x-1)-(5x+2)-6x≤-6 D. 3(2x-1)-(5x+2)-x≤-1
3. 小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少12元.”乙说:“至多10元.”丙说:“至多8元.”小明说:“你们三个人都说错了.”则这本书的价格x(元)所在的范围为 ( )
A. 8
A. 2
6. 一次函数 与 的图象如图,则下列结论:①k<0;②a>0;③当x<3时, y ;④方程 kx+b=x+a的解为x=3.其中正确结论的个数是 ( )
A. 0 B. 1 C. 2 D. 3
7. 已知关于x的不等式组 的整数解是-2,-1,0,1,2,3,4,若m,n为整数,则m+n的值是 ( )
A. 3 B. 4 C. 5或6 D. 6或7
8. 某矿泉水每瓶售价2元,现甲、乙两家商场给出优惠政策:甲商场全部9折,乙商场20瓶以上的部分8折.老师要小明去买一些矿泉水,小明想了想觉得到乙商场购买比较优惠.则小明需要购买的矿泉水的数量x(瓶)的取值范围是 ( )
A. x>30 B. x>40 C. x>50 D. x>60
9. 如图所示是按某影视厅放映电影的盈利y(元)与售出票数x(张)之间的函数关系画出的图象.要使放映一场电影的盈利不少于300 元,最少应卖出电影票的张数为 ( )
A. 85 B. 86
C. 84 D. 83
10. 我们定义例如: 若x满足 则x的整数解有 ( )
A. 0个 B. 1个 C. 2个 D. 3个
二、填空题(每小题3分,共18分)
11. 不等式2x-1≤4的最大整数解是 .
12. 已知关于x,y的方程组 的解满足不等式组则满足条件的m的整数值为 .
13. 已知实数x,y满足2x-3y=4,且x>-1,y≤2,设k=x-y,则k的取值范围是 .
14. 已知一次函数 和 ,当自变量x> -1时, ,则k的取值范围为
15. 对于三个数a,b,c,我们给出符号来表示其中最大(小)的数,规定 min{a,b,c}表示这三个数中最小的数, max{a,b,c}表示这三个数中最大的数.例如: min{-1,2,3} = - 1, max{-1,2,3}=3;若 min{4,x+4,4-x}= max{2,x+1,2x},则x的值为 .
16. 重庆一中初二年级老师为同学们购买《老人与海》、《泰戈尔诗集》和《雨的四季》供大家借阅,已知三种书单价之和为120元,计划购买三种书数量总共不超过125本,其中《老人与海》单价为50元,计划购买25本,《泰戈尔诗集》至少购买15本,《雨的四季》数量不少于《泰戈尔诗集》的2倍,在做预算时将《雨的四季》和《泰戈尔诗集》的单价弄反了,结果实际购买三种书的总价比预算多了116元,若三本书的单价均为整数,则实际购买这三种书最多需要花费 元.
三、解答题(共62分)
17. (8分)解不等式(组),并将解集在数轴上表示出来:
18. (8分)已知关于x的不等式
(1)若 是该不等式的解,求a的取值范围.
(2)在(1)的条件下,且: 不是该不等式的解,求符合题意的一个无理数a.
19. (10分)已知关于x的不等式组
(1)如果这个不等式组无解,求k的取值范围.
(2)如果这个不等式组有解,求k的取值范围.
(3)如果这个不等式组恰好有2 017个整数解,求k的取值范围.
20. (6分)请阅读求绝对值不等式 和 的解集的过程.
对于绝对值不等式 ,从图1 的数轴上看:大于 而小于3 的数的绝对值小于3,所以 的解集为
对于绝对值不等式 ,从图2的数轴上看:小于 而大于3的数的绝对值大于3,所以 的解集为 或
已知关于x,y的二元一次方程组 的解满足 ,其中m是负整数,求m的值.
21. (9分)已知直线 的图象经过点 ,且与直线 交于点
B(1,b).
(1)求直线 的表达式,并直接写出不等式 的解集.
(2)若O为坐标原点,直线 与x轴交于点 C,在x轴上是否存在一点 P,满足 若存在,求出此时点 P 的坐标;若不存在,请说明理由.
22. (10分)对于不等式: 且 当 时, 当 时, ,请根据以上信息,解答以下问题:
(1)解关于x的不等式:
(2)若关于x的不等式: 且 在 上存在x的值使其成立,求k的取值范围.
23. (11分)在今年的新冠疫情期间,政府紧急组织一批物资送往武汉.现已知这批物资中,食品和矿泉水共410箱,且食品比矿泉水多110箱.
(1)求食品和矿泉水各有多少箱
(2)现计划租用A,B两种货车共10辆,一次性将所有物资送到群众手中,已知A种货车最多可装食品40箱和矿泉水10箱,B种货车最多可装食品20箱和矿泉水20箱,试通过计算帮助政府设计出几种运输方案.
(3)在(2)条件下,A种货车每辆需付运费600元,B种货车每辆需付运费450元,政府应该选择哪种方案,才能使运费最少 最少运费是多少
第二章一元一次不等式和一元一次不等式组综合测试卷
C2. C3. D4. A5. B6. C7. C8. B9. C 10. B11. 212. - 2或-3 13. 1
17. 解:(1)去分母,得x-5+2>2x-6,解得x<3,在数轴上表示出来为:
②解不等式①,得x≤1,
解不等式②,得x>-2,故不等式组的解集为-2
(2)∵x=1不是该不等式的解,∴当x=1时,(x-5)( ax-3a+4)>0,即(1-5)(a-3a+4)>0,解得a>2,由(1)得a≤4,
∴满足x=1不是该不等式的解的无理数a可以是π.
19. 解:(1)根据题意,得-1≥1-k,解得k≥2.
(2)根据题意,得-1<1-k,解得k<2.
(3)∵不等式组恰好有2017个整数解,∴ - 1
②
得3x+3y= -3m-3,∴x+y= -m-1,
则-3≤-m-1≤3,解得-4≤m≤2,又∵m是负整数,
∴m的值为-4或-3或-2或-1.
21. 解:(1)由题意得两直线交点横坐标为1.
由图象知不等式 的解集为x≤1.
(2)存在.当y=0时,即-x+4=0,解得x=4,则C(4,0),设P(t,0),
解得t=10或t= - 2,∴P 点坐标为(-2,0),(10,0).
22. 解: ∴2x>2,解得x>1.
(2)由题意得,当a>1时,x-k<5x-2,解得 -1,解得k>6.
当0
23. 解:(1)设食品有x箱,矿泉水有y箱,依题意,
得:解得
即:食品有260箱,矿泉水有150箱.
(2)设租用A种货车m辆,则租用B种货车( 辆,
依题意,得: 解得:
又∵m为正整数,∴m可以为3,4,5,
∴共有3种运输方案,方案1:租用A种货车3 辆,B种货车7辆;
方案2:租用A种货车4辆,B种货车6辆;
方案3:租用A种货车5辆,B种货车5辆.
(3)选择方案1所需运费为 (元),选择方案2所需运费为 (元),选择方案3所需运费为 (元).
∴政府应该选择方案1,才能使运费最少,最少运费是4950元.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
