2024-2025学年上海市静安区久隆模范中学九年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年上海市静安区久隆模范中学九年级(上)期中数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1002.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-22 11:00:55 | ||
图片预览



文档简介
2024-2025学年上海市静安区久隆模范中学九年级(上)期中数学试卷
一、选择题:(本大题共6题,每题4分,共24分,下列各题四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题卡的相应位置上)
1.(4分)下列说法中,正确的是( )
A.有一个角相等的两个菱形必相似
B.有一条边相等的两个矩形必相似
C.有一个角相等的两个等腰三角形必相似
D.有一条边相等的两个等腰三角形必相似
2.(4分)已知二次函数的解析式为y=﹣x2+2x,下列关于函数图象的说法正确的是( )
A.对称轴是直线x=﹣1 B.图象经过原点
C.开口向上 D.图象有最低点
3.(4分)若两个相似三角形的面积比是1:9,则它们对应边的中线之比为( )
A.1:9 B.3:1 C.1:3 D.9:1
4.(4分)已知,下列说法中不正确的是( )
A.与方向相反 B.
C. D.
5.(4分)在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A.c=bsinB B.b=csinB C.a=btanB D.b=ctanB
6.(4分)如图,在 ABCD中,M、N为对角线BD上的两点,且BM:MN:ND=1:2:1,联结AM并延长交BC于点E,连接EN并延长交AD于点F,则AF:FD的值为( )
A.7:1 B.8:1 C.9:1 D.10:1
二、填空题(本大题共12小题,每题4分,共48分)
7.(4分)计算:= .
8.(4分)从地图上量得甲、乙两地的距离为6cm,而两地的实距离是300km,这幅地图的比例尺是 .
9.(4分)已知点M是线段AB的黄金分割点(AM<BM),若AB=4,则BM= .
10.(4分)如果抛物线y=(k﹣1)x2+kx﹣1(k是常数)的顶点在y轴上,那么该抛物线的顶点坐标为 .
11.(4分)在△ABC中,AB=3,AC=2,分别反向延长AB、AC到D、E,若AD=2,则当AE= 时,BC∥DE.
12.(4分)抛物线y=5(x﹣4)2+3向左平移2个单位长度,再向下平移1个单位长度,得到的新抛物线的顶点A关于直线x=4对称的点A′坐标是 .
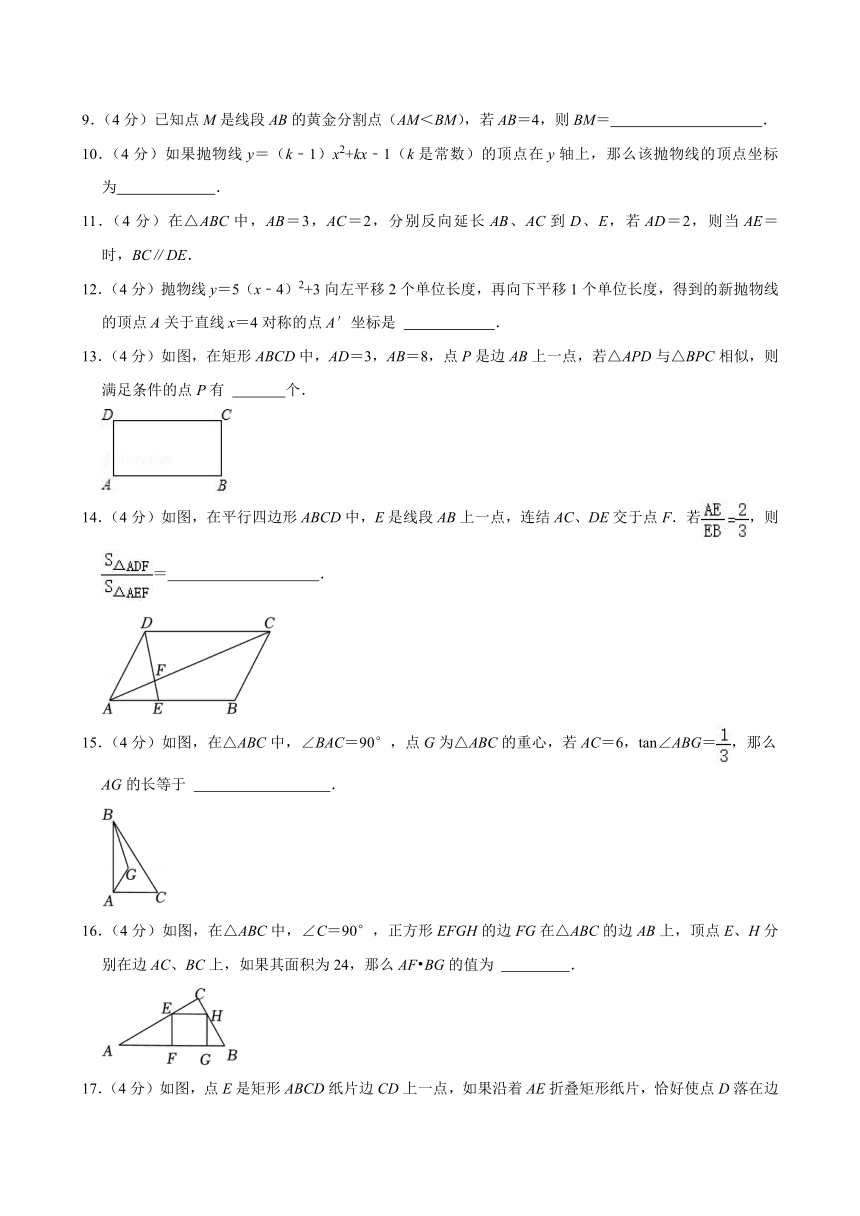
13.(4分)如图,在矩形ABCD中,AD=3,AB=8,点P是边AB上一点,若△APD与△BPC相似,则满足条件的点P有 个.
14.(4分)如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE交于点F.若,则= .
15.(4分)如图,在△ABC中,∠BAC=90°,点G为△ABC的重心,若AC=6,tan∠ABG=,那么AG的长等于 .
16.(4分)如图,在△ABC中,∠C=90°,正方形EFGH的边FG在△ABC的边AB上,顶点E、H分别在边AC、BC上,如果其面积为24,那么AF BG的值为 .
17.(4分)如图,点E是矩形ABCD纸片边CD上一点,如果沿着AE折叠矩形纸片,恰好使点D落在边BC上的点F处,已知BF=6cm,tan∠BAF=,那么折痕AE的长是 .
18.(4分)如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点C旋转得到△A′B′C,点A的对应点A′恰好与△ABC的重心重合,A′B′与BC相交于点E,如么CE:BC的值为 .
三、解答题:(本大题共7题,第19-22每题10分,第23-24每题13分,第25题14分,共78分,解答应写出文字说明,证明过程或演算步骤)
19.(10分)计算:.
20.(10分)已知,如图,点E在平行四边形ABCD的边CD上,且,设,.
(1)用、表示;(直接写出答案)
(2)设,在答题卷中所给的图上画出的结果.
21.(10分)如图,已知在四边形ABCD中,AD∥BC,∠ABC=90°,对角线AC、BD相交于点O,AD=2,AB=3,BC=4.
(1)求△BOC的面积;
(2)求∠ACD的正弦值.
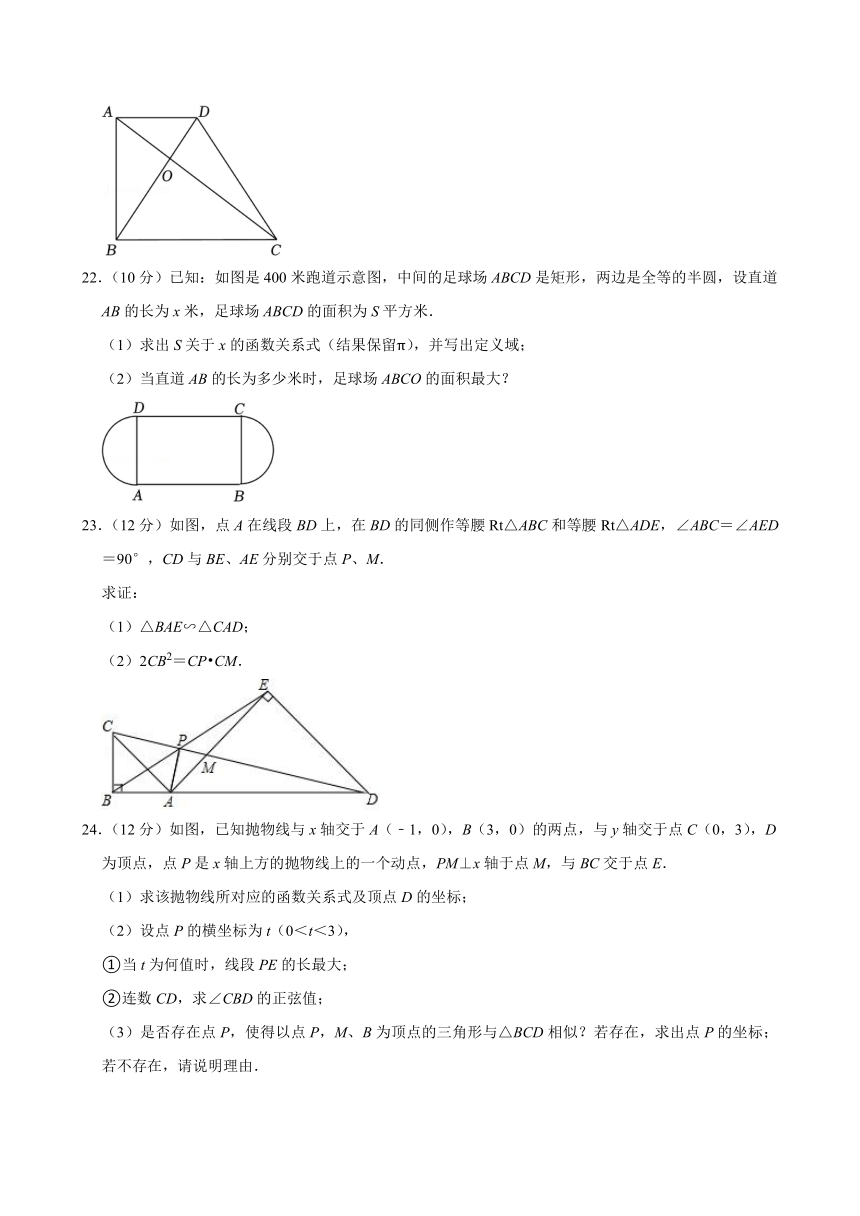
22.(10分)已知:如图是400米跑道示意图,中间的足球场ABCD是矩形,两边是全等的半圆,设直道AB的长为x米,足球场ABCD的面积为S平方米.
(1)求出S关于x的函数关系式(结果保留π),并写出定义域;
(2)当直道AB的长为多少米时,足球场ABCO的面积最大?
23.(12分)如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.
求证:
(1)△BAE∽△CAD;
(2)2CB2=CP CM.
24.(12分)如图,已知抛物线与x轴交于A(﹣1,0),B(3,0)的两点,与y轴交于点C(0,3),D为顶点,点P是x轴上方的抛物线上的一个动点,PM⊥x轴于点M,与BC交于点E.
(1)求该抛物线所对应的函数关系式及顶点D的坐标;
(2)设点P的横坐标为t(0<t<3),
①当t为何值时,线段PE的长最大;
②连数CD,求∠CBD的正弦值;
(3)是否存在点P,使得以点P,M、B为顶点的三角形与△BCD相似?若存在,求出点P的坐标;若不存在,请说明理由.
25.(14分)已知:如图,在梯形ABCD中,AD∥BC,∠BAD=90°,AD=2,AB=4,BC=5,在边BC上任取一点E,联结AE,作∠FEC=∠AEB,∠FEC的另一边EF交射线CD于点F.
(1)求cosC的值;
(2)如图1,当点F在线段CD上时,若,求BE的长;
(3)联结AF,当△AEF是直角三角形时,直接写出BE的长.
26.(附加题)
新定义1:将宽与长的比等于黄金分割比的矩形称为黄金矩形
新定义2:将顶角为36°的等腰三角形称为黄金三角形
①在一长矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平
②如图2,把这个正方形折成两个相等的矩形,再把纸片展平
③折出内侧矩形的对角线AB,并把AB折到图中所示的AD处
④展平纸片,按照所得到的点D折出DE
(1)报据以上折纸法,求证:矩形BCDE为黄金矩形;
(2)如图5,已知∠A=36°,△ABC为黄金三角形,BC=1,求AB的长;
(3)在(2)的条件下,截取BD=BC交AC于D,截取CE=CD交线段BD于E,过E作任意直线与边AB,BC交于P,Q两点,试判断:是否为定值,若是,请求出定值,请说明理由.
2024-2025学年上海市静安区久隆模范中学九年级(上)期中数学试卷
参考答案
一、选择题:(本大题共6题,每题4分,共24分,下列各题四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题卡的相应位置上)
1.(4分)下列说法中,正确的是( )
A.有一个角相等的两个菱形必相似
B.有一条边相等的两个矩形必相似
C.有一个角相等的两个等腰三角形必相似
D.有一条边相等的两个等腰三角形必相似
选:A.
2.(4分)已知二次函数的解析式为y=﹣x2+2x,下列关于函数图象的说法正确的是( )
A.对称轴是直线x=﹣1 B.图象经过原点
C.开口向上 D.图象有最低点
选:B.
3.(4分)若两个相似三角形的面积比是1:9,则它们对应边的中线之比为( )
A.1:9 B.3:1 C.1:3 D.9:1
选:C.
4.(4分)已知,下列说法中不正确的是( )
A.与方向相反 B.
C. D.
选:B.
5.(4分)在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A.c=bsinB B.b=csinB C.a=btanB D.b=ctanB
选:B.
6.(4分)如图,在 ABCD中,M、N为对角线BD上的两点,且BM:MN:ND=1:2:1,联结AM并延长交BC于点E,连接EN并延长交AD于点F,则AF:FD的值为( )
A.7:1 B.8:1 C.9:1 D.10:1
选:B.
二、填空题(本大题共12小题,每题4分,共48分)
7.(4分)计算:= .
8.(4分)从地图上量得甲、乙两地的距离为6cm,而两地的实距离是300km,这幅地图的比例尺是 1:5000000 .
9.(4分)已知点M是线段AB的黄金分割点(AM<BM),若AB=4,则BM= 2﹣2 .
10.(4分)如果抛物线y=(k﹣1)x2+kx﹣1(k是常数)的顶点在y轴上,那么该抛物线的顶点坐标为 (0,﹣1) .
11.(4分)在△ABC中,AB=3,AC=2,分别反向延长AB、AC到D、E,若AD=2,则当AE= 时,BC∥DE.
12.(4分)抛物线y=5(x﹣4)2+3向左平移2个单位长度,再向下平移1个单位长度,得到的新抛物线的顶点A关于直线x=4对称的点A′坐标是 (6,2) .
13.(4分)如图,在矩形ABCD中,AD=3,AB=8,点P是边AB上一点,若△APD与△BPC相似,则满足条件的点P有 3 个.
14.(4分)如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE交于点F.若,则= .
15.(4分)如图,在△ABC中,∠BAC=90°,点G为△ABC的重心,若AC=6,tan∠ABG=,那么AG的长等于 .
16.(4分)如图,在△ABC中,∠C=90°,正方形EFGH的边FG在△ABC的边AB上,顶点E、H分别在边AC、BC上,如果其面积为24,那么AF BG的值为 24 .
17.(4分)如图,点E是矩形ABCD纸片边CD上一点,如果沿着AE折叠矩形纸片,恰好使点D落在边BC上的点F处,已知BF=6cm,tan∠BAF=,那么折痕AE的长是 5cm .
18.(4分)如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点C旋转得到△A′B′C,点A的对应点A′恰好与△ABC的重心重合,A′B′与BC相交于点E,如么CE:BC的值为 .
三、解答题:(本大题共7题,第19-22每题10分,第23-24每题13分,第25题14分,共78分,解答应写出文字说明,证明过程或演算步骤)
19.(10分)计算:.
【解答】解:原式=+2×(1﹣)+4×
=+2﹣+2
=﹣2﹣+2﹣+2
=2﹣.
20.(10分)已知,如图,点E在平行四边形ABCD的边CD上,且,设,.
(1)用、表示;(直接写出答案)
(2)设,在答题卷中所给的图上画出的结果.
【解答】解:(1)∵=,即DE=CE,DE=DC,
=+
(2)如图所示:延长AE、BC交于G,则即为的结果.
∵四边形ABCD是平行四边形
∴AD∥BC
∴==
∴AG=3AE
又∵
∴=3
∴=.
21.(10分)如图,已知在四边形ABCD中,AD∥BC,∠ABC=90°,对角线AC、BD相交于点O,AD=2,AB=3,BC=4.
(1)求△BOC的面积;
(2)求∠ACD的正弦值.
【解答】解:(1)过点O作AB的平行线,分别与AD,BC交于点M,N,
∵AD∥BC,MN∥AB,
∴四边形ABNM是平行四边形,
又∵∠ABC=90°,
∴四边形ABNM是矩形,
∴OM⊥AD,ON⊥BC.
∵AD∥BC,
∴△AOD∽△COB,
∴,
又∵MN=AB=3,
∴OM=1,ON=2,
∴.
(2)在Rt△ABC中,
AC=.
过点D作BC的垂线,垂足为E,过点A作CD垂线,垂足为F,
在Rt△CDE中,
CD=.
∵,
∴AF=.
在Rt△CAF中,
sin∠ACD=.
22.(10分)已知:如图是400米跑道示意图,中间的足球场ABCD是矩形,两边是全等的半圆,设直道AB的长为x米,足球场ABCD的面积为S平方米.
(1)求出S关于x的函数关系式(结果保留π),并写出定义域;
(2)当直道AB的长为多少米时,足球场ABCO的面积最大?
【解答】解:(1)根据题意,得2x+π =400,
解得S=﹣x2+x,
∵S>0,即﹣x2+x>0,且x>0,
∴0<x<200,
∴S关于x的函数关系式及定义域是S=﹣x2+x(0<x<200).
(2)S=﹣x2+x=﹣(x﹣100)2+,
∴当x=100时,S的值最大,
∴当直道AB的长为100米时,足球场ABCO的面积最大.
23.(12分)如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.
求证:
(1)△BAE∽△CAD;
(2)2CB2=CP CM.
【解答】(1)证明:∵等腰Rt△ABC和等腰Rt△ADE,∠ABC=∠AED=90°,
∴AC=AB,AD=AE,∠BAC=∠EAD=45°
∴
∵∠BAC=∠EAD
∴∠BAE=∠CAD
∴△BAE∽△CAD
(2)∵△BAE∽△CAD,
∴∠BEA=∠CDA,
∵∠PME=∠AMD
∴△PME∽△AMD
∴,且∠PMA=∠DME,
∴△PMA∽△EMD,
∴∠APD=∠AED=90°,
∵∠CAE=180°﹣∠BAC﹣∠EAD=90°,且∠ACP=∠ACM,
∴△CAP∽△CMA,
∴,
∴AC2=CP CM,
∵AC=AB
∴2CB2=CP CM
24.(12分)如图,已知抛物线与x轴交于A(﹣1,0),B(3,0)的两点,与y轴交于点C(0,3),D为顶点,点P是x轴上方的抛物线上的一个动点,PM⊥x轴于点M,与BC交于点E.
(1)求该抛物线所对应的函数关系式及顶点D的坐标;
(2)设点P的横坐标为t(0<t<3),
①当t为何值时,线段PE的长最大;
②连数CD,求∠CBD的正弦值;
(3)是否存在点P,使得以点P,M、B为顶点的三角形与△BCD相似?若存在,求出点P的坐标;若不存在,请说明理由.
【解答】解:(1)设抛物线解析式为y=ax2+bx+c(a≠0),
∵抛物线与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,3),
∴,
解得,
∴抛物线所对应的函数关系式y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线的顶点为D(1,4);
(2)①抛物线y=﹣x2+2x+3与x轴交点坐标为A(﹣1,0),B(3,0).
设直线BC的函数关系式为y=kx+b(k≠0),
则,
解得,
直线BC的函数关系式为y=﹣x+3.
设P(t,﹣t2+2t+3),则E(t,﹣t+3).
∴,
∵a=﹣1<0,且0<t<3,
∴当时,线段PE的长最大值为;
②∵B(3,0),C(0,3),D(1,4),
则,,,
∵BC2+CD2=BD2,
∴△BCD为直角三角形,如图1,
∴sin∠CBD===;
(3)存在点P,使得以点P,M、B为顶点的三角形与△BCD相似;理由如下:
由(2)知△BCD是直角三角形,且∠BCD=90°,CD=,BC=3.
(Ⅰ) 如图2,若△PMB∽△BCD,则,
即,
整理,得t2﹣5t+6=0,
解得t1=2,t2=3(舍去).
∴P(2,3).
(Ⅱ) 如图3,若△BMP∽△BCD,
则,
即,
整理,得3t2﹣7t﹣6=0,
解得,t2=3(舍去).
∴.
故符合条件的点P的坐标为P(2,3)或.
25.(14分)已知:如图,在梯形ABCD中,AD∥BC,∠BAD=90°,AD=2,AB=4,BC=5,在边BC上任取一点E,联结AE,作∠FEC=∠AEB,∠FEC的另一边EF交射线CD于点F.
(1)求cosC的值;
(2)如图1,当点F在线段CD上时,若,求BE的长;
(3)联结AF,当△AEF是直角三角形时,直接写出BE的长.
【解答】解:(1)如图1,过点D作DG⊥BC于G,则∠DGC=90°,
∵AD∥BC,
∴∠A+∠B=180°,
∵∠A=90°,
∴∠B=90°,
∴∠B=∠DGC,
∴AB∥DG,
∴四边形ABGD是矩形,
∴BG=AD=2,DG=AB=4,
∵BC=5,
∴CG=5﹣2=3,
由勾股定理得:DC==5,
∴cosC==;
(2)如图2,过点F作FH⊥BC于H,
∵CD=5,=,
∴CF=5×=,
由(1)知:cosC==,
∴=,
∴CH=2,
由勾股定理得:FH===,
设BE=a,则EH=5﹣2﹣a=3﹣a,
∵∠AEB=∠FEC,
∴tan∠AEB=tan∠FEC,
∴=,即=,
解得:a=,
∴BE=;
(3)分三种情况:
①当∠AEF=90°时,如图3,
∴∠AEB+∠FEC=180°﹣90°=90°,
∵∠AEB=∠FEC,
∴∠AEB=45°,
∵∠B=90°,
∴△AEB是等腰直角三角形,
∴BE=AE=4;
②当∠AFE=90°时,如图4,延长EF和AD交于点Q,过点E作EM⊥AD于M,过点F作FP⊥AD于P,
∵AD∥BC,
∴∠AEB=∠EAD,∠FEC=∠Q,
∵∠AEB=∠FEC,
∴∠Q=∠EAD,
∴AE=EQ,
∴AM=MQ,
同理得四边形ABEM是矩形,
设DM=x,则AM=MQ=2+x,
∴BE=AM=2+x,CE=5﹣(2+x)=3﹣x,
∵DQ∥CE,
∴△DFQ∽△CFE,
∴=,即=,
∴DF=,
∵AD∥BC,
∴∠C=∠QDF,
∴cosC=cos∠QDF,
∴=,
∴PD:PF:DF=3:4:5,
∴PF=,PD=,
∵∠AFE=90°,
∴∠AFQ=90°,
∴∠Q+∠FAQ=90°,
∵∠BAE+∠AEB=90°,
∵∠AEB=∠Q,
∴∠BAE=∠FAQ,
∴tan∠BAE=tan∠FAQ,
∴=,即=,
解得:x1=x2=0,
经检验:x=0是原方程的解,且符合题意;
∴BE=2;
③当∠EAF=90°时,如图5,过点E作EM⊥AD于M,过点F作FP⊥AD于P,
设AM=m,
同理得:AM=MG=BE=m,DG=2﹣2m,
∵AD∥BC,
∴△FGD∽△FEC,
∴=,即=,
∴DF=,DP=,FP=,
同理可得:∠FAP=∠BAE,
∴tan∠BAE=tan∠FAP,
∴=,即=,
解得:m1=﹣2+2,m2=﹣2﹣2(舍);
经检验,m=﹣2+2是原方程的解,
∴BE=2﹣2,
综上,BE的长为4或2或2﹣2.
26.(附加题)
新定义1:将宽与长的比等于黄金分割比的矩形称为黄金矩形
新定义2:将顶角为36°的等腰三角形称为黄金三角形
①在一长矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平
②如图2,把这个正方形折成两个相等的矩形,再把纸片展平
③折出内侧矩形的对角线AB,并把AB折到图中所示的AD处
④展平纸片,按照所得到的点D折出DE
(1)报据以上折纸法,求证:矩形BCDE为黄金矩形;
(2)如图5,已知∠A=36°,△ABC为黄金三角形,BC=1,求AB的长;
(3)在(2)的条件下,截取BD=BC交AC于D,截取CE=CD交线段BD于E,过E作任意直线与边AB,BC交于P,Q两点,试判断:是否为定值,若是,请求出定值,请说明理由.
【解答】(1)证明:由折叠可知:∠MBC=∠MNC=90°,
又∵∠NMB=90°,
∴四边形MNCB是矩形,
由折叠的性质得:MB=MN,
∴四边形MNCB是正方形,
∴BC=MN=CN,∠NCB=90°,
由题意得,
∴;
由折叠的性质得,
∴,
∴,
∴矩形BCDE是黄金矩形;
(2)解:如图5所示,作∠ABC的角平分线交AC于D,
∵∠A=36°,AB=AC,
∴,
∴,
∴AD=BD,∠BDC=180°﹣36°﹣72°=72°,
∴∠BDC=∠C,
∴AD=BD=BC=1,
又∵∠C=∠C,
∴△ABC∽△BDC,
∴,即,
∴,
∴AB2﹣AB﹣1=0,
解得或(舍去),
经检验,是原方程的解;
(3)解:为定值;理由如下:
如图6,过点E分别作AB,BC的垂线,垂足分别为F,G,过点Q作QH⊥AB于H,
∵S△BPQ=S△BPE+S△BQE,
∴;
由(2)可知,当BD平分∠ABC时有BD=BC,
∴EG=EF,
∴BP QH=(BP+BQ) EG,
在Rt△BQH中,QH=BQ sin∠QBH,
∴BP BQ sin∠QBH=(BP+BQ) EG,
∴,
∴,
在Rt△EBG中,EG=BE sin∠EBG,
∴;
∵CE=CD,
∴∠CED=∠CDE=72°,
∴∠ECD=36°,
∴∠ECB=36°=∠EBC,
∴,
∴,
∴,
∵,∠GBE=∠EBF,
∴,
如图6所示,连接AF,
在Rt△ABF中,,
∵,
∴
=
=
=
=.
一、选择题:(本大题共6题,每题4分,共24分,下列各题四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题卡的相应位置上)
1.(4分)下列说法中,正确的是( )
A.有一个角相等的两个菱形必相似
B.有一条边相等的两个矩形必相似
C.有一个角相等的两个等腰三角形必相似
D.有一条边相等的两个等腰三角形必相似
2.(4分)已知二次函数的解析式为y=﹣x2+2x,下列关于函数图象的说法正确的是( )
A.对称轴是直线x=﹣1 B.图象经过原点
C.开口向上 D.图象有最低点
3.(4分)若两个相似三角形的面积比是1:9,则它们对应边的中线之比为( )
A.1:9 B.3:1 C.1:3 D.9:1
4.(4分)已知,下列说法中不正确的是( )
A.与方向相反 B.
C. D.
5.(4分)在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A.c=bsinB B.b=csinB C.a=btanB D.b=ctanB
6.(4分)如图,在 ABCD中,M、N为对角线BD上的两点,且BM:MN:ND=1:2:1,联结AM并延长交BC于点E,连接EN并延长交AD于点F,则AF:FD的值为( )
A.7:1 B.8:1 C.9:1 D.10:1
二、填空题(本大题共12小题,每题4分,共48分)
7.(4分)计算:= .
8.(4分)从地图上量得甲、乙两地的距离为6cm,而两地的实距离是300km,这幅地图的比例尺是 .
9.(4分)已知点M是线段AB的黄金分割点(AM<BM),若AB=4,则BM= .
10.(4分)如果抛物线y=(k﹣1)x2+kx﹣1(k是常数)的顶点在y轴上,那么该抛物线的顶点坐标为 .
11.(4分)在△ABC中,AB=3,AC=2,分别反向延长AB、AC到D、E,若AD=2,则当AE= 时,BC∥DE.
12.(4分)抛物线y=5(x﹣4)2+3向左平移2个单位长度,再向下平移1个单位长度,得到的新抛物线的顶点A关于直线x=4对称的点A′坐标是 .
13.(4分)如图,在矩形ABCD中,AD=3,AB=8,点P是边AB上一点,若△APD与△BPC相似,则满足条件的点P有 个.
14.(4分)如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE交于点F.若,则= .
15.(4分)如图,在△ABC中,∠BAC=90°,点G为△ABC的重心,若AC=6,tan∠ABG=,那么AG的长等于 .
16.(4分)如图,在△ABC中,∠C=90°,正方形EFGH的边FG在△ABC的边AB上,顶点E、H分别在边AC、BC上,如果其面积为24,那么AF BG的值为 .
17.(4分)如图,点E是矩形ABCD纸片边CD上一点,如果沿着AE折叠矩形纸片,恰好使点D落在边BC上的点F处,已知BF=6cm,tan∠BAF=,那么折痕AE的长是 .
18.(4分)如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点C旋转得到△A′B′C,点A的对应点A′恰好与△ABC的重心重合,A′B′与BC相交于点E,如么CE:BC的值为 .
三、解答题:(本大题共7题,第19-22每题10分,第23-24每题13分,第25题14分,共78分,解答应写出文字说明,证明过程或演算步骤)
19.(10分)计算:.
20.(10分)已知,如图,点E在平行四边形ABCD的边CD上,且,设,.
(1)用、表示;(直接写出答案)
(2)设,在答题卷中所给的图上画出的结果.
21.(10分)如图,已知在四边形ABCD中,AD∥BC,∠ABC=90°,对角线AC、BD相交于点O,AD=2,AB=3,BC=4.
(1)求△BOC的面积;
(2)求∠ACD的正弦值.
22.(10分)已知:如图是400米跑道示意图,中间的足球场ABCD是矩形,两边是全等的半圆,设直道AB的长为x米,足球场ABCD的面积为S平方米.
(1)求出S关于x的函数关系式(结果保留π),并写出定义域;
(2)当直道AB的长为多少米时,足球场ABCO的面积最大?
23.(12分)如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.
求证:
(1)△BAE∽△CAD;
(2)2CB2=CP CM.
24.(12分)如图,已知抛物线与x轴交于A(﹣1,0),B(3,0)的两点,与y轴交于点C(0,3),D为顶点,点P是x轴上方的抛物线上的一个动点,PM⊥x轴于点M,与BC交于点E.
(1)求该抛物线所对应的函数关系式及顶点D的坐标;
(2)设点P的横坐标为t(0<t<3),
①当t为何值时,线段PE的长最大;
②连数CD,求∠CBD的正弦值;
(3)是否存在点P,使得以点P,M、B为顶点的三角形与△BCD相似?若存在,求出点P的坐标;若不存在,请说明理由.
25.(14分)已知:如图,在梯形ABCD中,AD∥BC,∠BAD=90°,AD=2,AB=4,BC=5,在边BC上任取一点E,联结AE,作∠FEC=∠AEB,∠FEC的另一边EF交射线CD于点F.
(1)求cosC的值;
(2)如图1,当点F在线段CD上时,若,求BE的长;
(3)联结AF,当△AEF是直角三角形时,直接写出BE的长.
26.(附加题)
新定义1:将宽与长的比等于黄金分割比的矩形称为黄金矩形
新定义2:将顶角为36°的等腰三角形称为黄金三角形
①在一长矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平
②如图2,把这个正方形折成两个相等的矩形,再把纸片展平
③折出内侧矩形的对角线AB,并把AB折到图中所示的AD处
④展平纸片,按照所得到的点D折出DE
(1)报据以上折纸法,求证:矩形BCDE为黄金矩形;
(2)如图5,已知∠A=36°,△ABC为黄金三角形,BC=1,求AB的长;
(3)在(2)的条件下,截取BD=BC交AC于D,截取CE=CD交线段BD于E,过E作任意直线与边AB,BC交于P,Q两点,试判断:是否为定值,若是,请求出定值,请说明理由.
2024-2025学年上海市静安区久隆模范中学九年级(上)期中数学试卷
参考答案
一、选择题:(本大题共6题,每题4分,共24分,下列各题四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题卡的相应位置上)
1.(4分)下列说法中,正确的是( )
A.有一个角相等的两个菱形必相似
B.有一条边相等的两个矩形必相似
C.有一个角相等的两个等腰三角形必相似
D.有一条边相等的两个等腰三角形必相似
选:A.
2.(4分)已知二次函数的解析式为y=﹣x2+2x,下列关于函数图象的说法正确的是( )
A.对称轴是直线x=﹣1 B.图象经过原点
C.开口向上 D.图象有最低点
选:B.
3.(4分)若两个相似三角形的面积比是1:9,则它们对应边的中线之比为( )
A.1:9 B.3:1 C.1:3 D.9:1
选:C.
4.(4分)已知,下列说法中不正确的是( )
A.与方向相反 B.
C. D.
选:B.
5.(4分)在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A.c=bsinB B.b=csinB C.a=btanB D.b=ctanB
选:B.
6.(4分)如图,在 ABCD中,M、N为对角线BD上的两点,且BM:MN:ND=1:2:1,联结AM并延长交BC于点E,连接EN并延长交AD于点F,则AF:FD的值为( )
A.7:1 B.8:1 C.9:1 D.10:1
选:B.
二、填空题(本大题共12小题,每题4分,共48分)
7.(4分)计算:= .
8.(4分)从地图上量得甲、乙两地的距离为6cm,而两地的实距离是300km,这幅地图的比例尺是 1:5000000 .
9.(4分)已知点M是线段AB的黄金分割点(AM<BM),若AB=4,则BM= 2﹣2 .
10.(4分)如果抛物线y=(k﹣1)x2+kx﹣1(k是常数)的顶点在y轴上,那么该抛物线的顶点坐标为 (0,﹣1) .
11.(4分)在△ABC中,AB=3,AC=2,分别反向延长AB、AC到D、E,若AD=2,则当AE= 时,BC∥DE.
12.(4分)抛物线y=5(x﹣4)2+3向左平移2个单位长度,再向下平移1个单位长度,得到的新抛物线的顶点A关于直线x=4对称的点A′坐标是 (6,2) .
13.(4分)如图,在矩形ABCD中,AD=3,AB=8,点P是边AB上一点,若△APD与△BPC相似,则满足条件的点P有 3 个.
14.(4分)如图,在平行四边形ABCD中,E是线段AB上一点,连结AC、DE交于点F.若,则= .
15.(4分)如图,在△ABC中,∠BAC=90°,点G为△ABC的重心,若AC=6,tan∠ABG=,那么AG的长等于 .
16.(4分)如图,在△ABC中,∠C=90°,正方形EFGH的边FG在△ABC的边AB上,顶点E、H分别在边AC、BC上,如果其面积为24,那么AF BG的值为 24 .
17.(4分)如图,点E是矩形ABCD纸片边CD上一点,如果沿着AE折叠矩形纸片,恰好使点D落在边BC上的点F处,已知BF=6cm,tan∠BAF=,那么折痕AE的长是 5cm .
18.(4分)如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点C旋转得到△A′B′C,点A的对应点A′恰好与△ABC的重心重合,A′B′与BC相交于点E,如么CE:BC的值为 .
三、解答题:(本大题共7题,第19-22每题10分,第23-24每题13分,第25题14分,共78分,解答应写出文字说明,证明过程或演算步骤)
19.(10分)计算:.
【解答】解:原式=+2×(1﹣)+4×
=+2﹣+2
=﹣2﹣+2﹣+2
=2﹣.
20.(10分)已知,如图,点E在平行四边形ABCD的边CD上,且,设,.
(1)用、表示;(直接写出答案)
(2)设,在答题卷中所给的图上画出的结果.
【解答】解:(1)∵=,即DE=CE,DE=DC,
=+
(2)如图所示:延长AE、BC交于G,则即为的结果.
∵四边形ABCD是平行四边形
∴AD∥BC
∴==
∴AG=3AE
又∵
∴=3
∴=.
21.(10分)如图,已知在四边形ABCD中,AD∥BC,∠ABC=90°,对角线AC、BD相交于点O,AD=2,AB=3,BC=4.
(1)求△BOC的面积;
(2)求∠ACD的正弦值.
【解答】解:(1)过点O作AB的平行线,分别与AD,BC交于点M,N,
∵AD∥BC,MN∥AB,
∴四边形ABNM是平行四边形,
又∵∠ABC=90°,
∴四边形ABNM是矩形,
∴OM⊥AD,ON⊥BC.
∵AD∥BC,
∴△AOD∽△COB,
∴,
又∵MN=AB=3,
∴OM=1,ON=2,
∴.
(2)在Rt△ABC中,
AC=.
过点D作BC的垂线,垂足为E,过点A作CD垂线,垂足为F,
在Rt△CDE中,
CD=.
∵,
∴AF=.
在Rt△CAF中,
sin∠ACD=.
22.(10分)已知:如图是400米跑道示意图,中间的足球场ABCD是矩形,两边是全等的半圆,设直道AB的长为x米,足球场ABCD的面积为S平方米.
(1)求出S关于x的函数关系式(结果保留π),并写出定义域;
(2)当直道AB的长为多少米时,足球场ABCO的面积最大?
【解答】解:(1)根据题意,得2x+π =400,
解得S=﹣x2+x,
∵S>0,即﹣x2+x>0,且x>0,
∴0<x<200,
∴S关于x的函数关系式及定义域是S=﹣x2+x(0<x<200).
(2)S=﹣x2+x=﹣(x﹣100)2+,
∴当x=100时,S的值最大,
∴当直道AB的长为100米时,足球场ABCO的面积最大.
23.(12分)如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.
求证:
(1)△BAE∽△CAD;
(2)2CB2=CP CM.
【解答】(1)证明:∵等腰Rt△ABC和等腰Rt△ADE,∠ABC=∠AED=90°,
∴AC=AB,AD=AE,∠BAC=∠EAD=45°
∴
∵∠BAC=∠EAD
∴∠BAE=∠CAD
∴△BAE∽△CAD
(2)∵△BAE∽△CAD,
∴∠BEA=∠CDA,
∵∠PME=∠AMD
∴△PME∽△AMD
∴,且∠PMA=∠DME,
∴△PMA∽△EMD,
∴∠APD=∠AED=90°,
∵∠CAE=180°﹣∠BAC﹣∠EAD=90°,且∠ACP=∠ACM,
∴△CAP∽△CMA,
∴,
∴AC2=CP CM,
∵AC=AB
∴2CB2=CP CM
24.(12分)如图,已知抛物线与x轴交于A(﹣1,0),B(3,0)的两点,与y轴交于点C(0,3),D为顶点,点P是x轴上方的抛物线上的一个动点,PM⊥x轴于点M,与BC交于点E.
(1)求该抛物线所对应的函数关系式及顶点D的坐标;
(2)设点P的横坐标为t(0<t<3),
①当t为何值时,线段PE的长最大;
②连数CD,求∠CBD的正弦值;
(3)是否存在点P,使得以点P,M、B为顶点的三角形与△BCD相似?若存在,求出点P的坐标;若不存在,请说明理由.
【解答】解:(1)设抛物线解析式为y=ax2+bx+c(a≠0),
∵抛物线与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,3),
∴,
解得,
∴抛物线所对应的函数关系式y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴抛物线的顶点为D(1,4);
(2)①抛物线y=﹣x2+2x+3与x轴交点坐标为A(﹣1,0),B(3,0).
设直线BC的函数关系式为y=kx+b(k≠0),
则,
解得,
直线BC的函数关系式为y=﹣x+3.
设P(t,﹣t2+2t+3),则E(t,﹣t+3).
∴,
∵a=﹣1<0,且0<t<3,
∴当时,线段PE的长最大值为;
②∵B(3,0),C(0,3),D(1,4),
则,,,
∵BC2+CD2=BD2,
∴△BCD为直角三角形,如图1,
∴sin∠CBD===;
(3)存在点P,使得以点P,M、B为顶点的三角形与△BCD相似;理由如下:
由(2)知△BCD是直角三角形,且∠BCD=90°,CD=,BC=3.
(Ⅰ) 如图2,若△PMB∽△BCD,则,
即,
整理,得t2﹣5t+6=0,
解得t1=2,t2=3(舍去).
∴P(2,3).
(Ⅱ) 如图3,若△BMP∽△BCD,
则,
即,
整理,得3t2﹣7t﹣6=0,
解得,t2=3(舍去).
∴.
故符合条件的点P的坐标为P(2,3)或.
25.(14分)已知:如图,在梯形ABCD中,AD∥BC,∠BAD=90°,AD=2,AB=4,BC=5,在边BC上任取一点E,联结AE,作∠FEC=∠AEB,∠FEC的另一边EF交射线CD于点F.
(1)求cosC的值;
(2)如图1,当点F在线段CD上时,若,求BE的长;
(3)联结AF,当△AEF是直角三角形时,直接写出BE的长.
【解答】解:(1)如图1,过点D作DG⊥BC于G,则∠DGC=90°,
∵AD∥BC,
∴∠A+∠B=180°,
∵∠A=90°,
∴∠B=90°,
∴∠B=∠DGC,
∴AB∥DG,
∴四边形ABGD是矩形,
∴BG=AD=2,DG=AB=4,
∵BC=5,
∴CG=5﹣2=3,
由勾股定理得:DC==5,
∴cosC==;
(2)如图2,过点F作FH⊥BC于H,
∵CD=5,=,
∴CF=5×=,
由(1)知:cosC==,
∴=,
∴CH=2,
由勾股定理得:FH===,
设BE=a,则EH=5﹣2﹣a=3﹣a,
∵∠AEB=∠FEC,
∴tan∠AEB=tan∠FEC,
∴=,即=,
解得:a=,
∴BE=;
(3)分三种情况:
①当∠AEF=90°时,如图3,
∴∠AEB+∠FEC=180°﹣90°=90°,
∵∠AEB=∠FEC,
∴∠AEB=45°,
∵∠B=90°,
∴△AEB是等腰直角三角形,
∴BE=AE=4;
②当∠AFE=90°时,如图4,延长EF和AD交于点Q,过点E作EM⊥AD于M,过点F作FP⊥AD于P,
∵AD∥BC,
∴∠AEB=∠EAD,∠FEC=∠Q,
∵∠AEB=∠FEC,
∴∠Q=∠EAD,
∴AE=EQ,
∴AM=MQ,
同理得四边形ABEM是矩形,
设DM=x,则AM=MQ=2+x,
∴BE=AM=2+x,CE=5﹣(2+x)=3﹣x,
∵DQ∥CE,
∴△DFQ∽△CFE,
∴=,即=,
∴DF=,
∵AD∥BC,
∴∠C=∠QDF,
∴cosC=cos∠QDF,
∴=,
∴PD:PF:DF=3:4:5,
∴PF=,PD=,
∵∠AFE=90°,
∴∠AFQ=90°,
∴∠Q+∠FAQ=90°,
∵∠BAE+∠AEB=90°,
∵∠AEB=∠Q,
∴∠BAE=∠FAQ,
∴tan∠BAE=tan∠FAQ,
∴=,即=,
解得:x1=x2=0,
经检验:x=0是原方程的解,且符合题意;
∴BE=2;
③当∠EAF=90°时,如图5,过点E作EM⊥AD于M,过点F作FP⊥AD于P,
设AM=m,
同理得:AM=MG=BE=m,DG=2﹣2m,
∵AD∥BC,
∴△FGD∽△FEC,
∴=,即=,
∴DF=,DP=,FP=,
同理可得:∠FAP=∠BAE,
∴tan∠BAE=tan∠FAP,
∴=,即=,
解得:m1=﹣2+2,m2=﹣2﹣2(舍);
经检验,m=﹣2+2是原方程的解,
∴BE=2﹣2,
综上,BE的长为4或2或2﹣2.
26.(附加题)
新定义1:将宽与长的比等于黄金分割比的矩形称为黄金矩形
新定义2:将顶角为36°的等腰三角形称为黄金三角形
①在一长矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平
②如图2,把这个正方形折成两个相等的矩形,再把纸片展平
③折出内侧矩形的对角线AB,并把AB折到图中所示的AD处
④展平纸片,按照所得到的点D折出DE
(1)报据以上折纸法,求证:矩形BCDE为黄金矩形;
(2)如图5,已知∠A=36°,△ABC为黄金三角形,BC=1,求AB的长;
(3)在(2)的条件下,截取BD=BC交AC于D,截取CE=CD交线段BD于E,过E作任意直线与边AB,BC交于P,Q两点,试判断:是否为定值,若是,请求出定值,请说明理由.
【解答】(1)证明:由折叠可知:∠MBC=∠MNC=90°,
又∵∠NMB=90°,
∴四边形MNCB是矩形,
由折叠的性质得:MB=MN,
∴四边形MNCB是正方形,
∴BC=MN=CN,∠NCB=90°,
由题意得,
∴;
由折叠的性质得,
∴,
∴,
∴矩形BCDE是黄金矩形;
(2)解:如图5所示,作∠ABC的角平分线交AC于D,
∵∠A=36°,AB=AC,
∴,
∴,
∴AD=BD,∠BDC=180°﹣36°﹣72°=72°,
∴∠BDC=∠C,
∴AD=BD=BC=1,
又∵∠C=∠C,
∴△ABC∽△BDC,
∴,即,
∴,
∴AB2﹣AB﹣1=0,
解得或(舍去),
经检验,是原方程的解;
(3)解:为定值;理由如下:
如图6,过点E分别作AB,BC的垂线,垂足分别为F,G,过点Q作QH⊥AB于H,
∵S△BPQ=S△BPE+S△BQE,
∴;
由(2)可知,当BD平分∠ABC时有BD=BC,
∴EG=EF,
∴BP QH=(BP+BQ) EG,
在Rt△BQH中,QH=BQ sin∠QBH,
∴BP BQ sin∠QBH=(BP+BQ) EG,
∴,
∴,
在Rt△EBG中,EG=BE sin∠EBG,
∴;
∵CE=CD,
∴∠CED=∠CDE=72°,
∴∠ECD=36°,
∴∠ECB=36°=∠EBC,
∴,
∴,
∴,
∵,∠GBE=∠EBF,
∴,
如图6所示,连接AF,
在Rt△ABF中,,
∵,
∴
=
=
=
=.
同课章节目录
