北师大版数学八年级上册期末复习题一(含解析)
文档属性
| 名称 | 北师大版数学八年级上册期末复习题一(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 388.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-21 22:03:12 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版数学八年级上册期末复习题一
一、单选题
1.在0,,,,,,3.14,,相邻两个1之间0的个数逐次加1)中,无理数的个数有( )
A.2个 B.3个 C.4个 D.5个
2. 在长方形中,,,是边上一点,连接,把沿翻折,点恰好落在边上的处,延长,与的平分线交于点,交于点,则的长度为( )
A. B. C.4 D.
3.数据12,10,13,8,17,10,21的中位数是( )
A.8 B.10 C.13 D.12
4.如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=40°时,∠1的度数为( )
A.40° B.45° C.50° D.55°
5.化简的结果是( )
A. B. C. D.
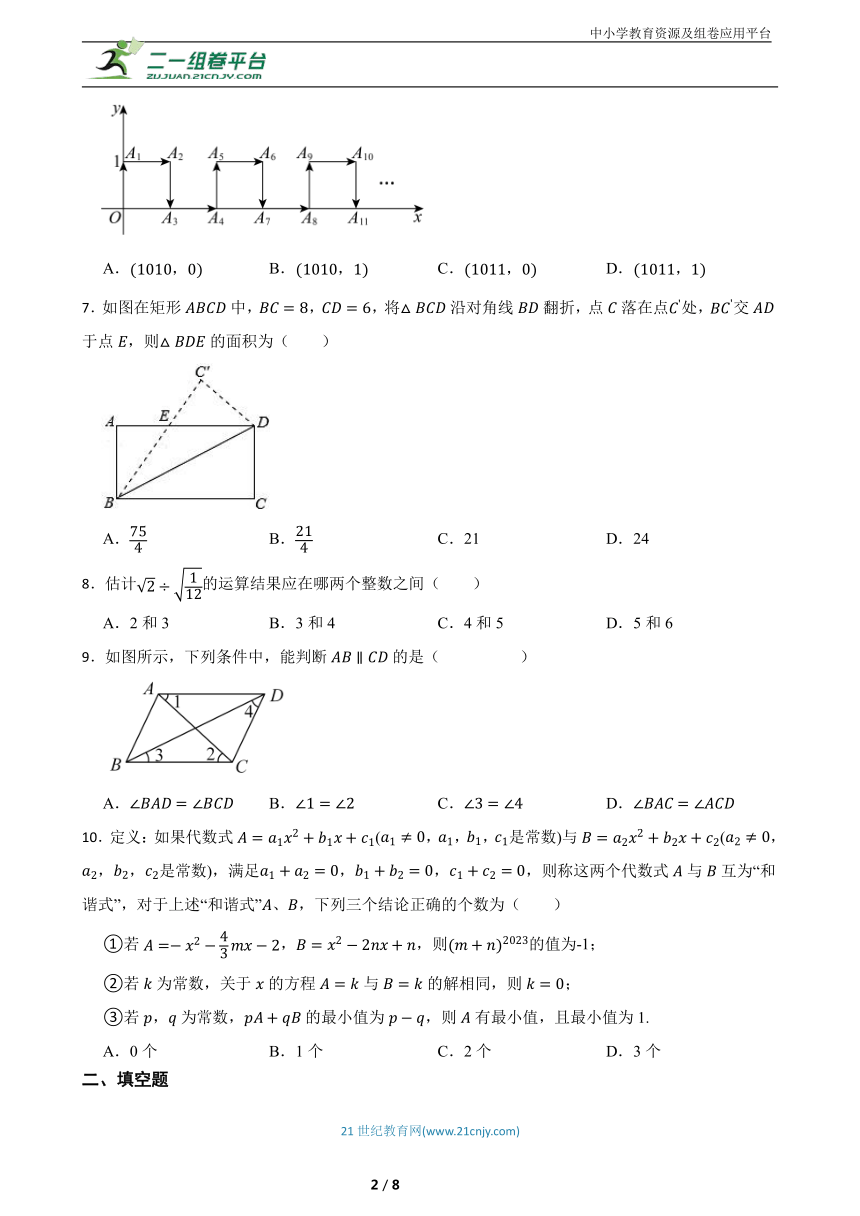
6.在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点,第二次移动到点,…,第n次移动到点,则点的坐标是( )
A. B. C. D.
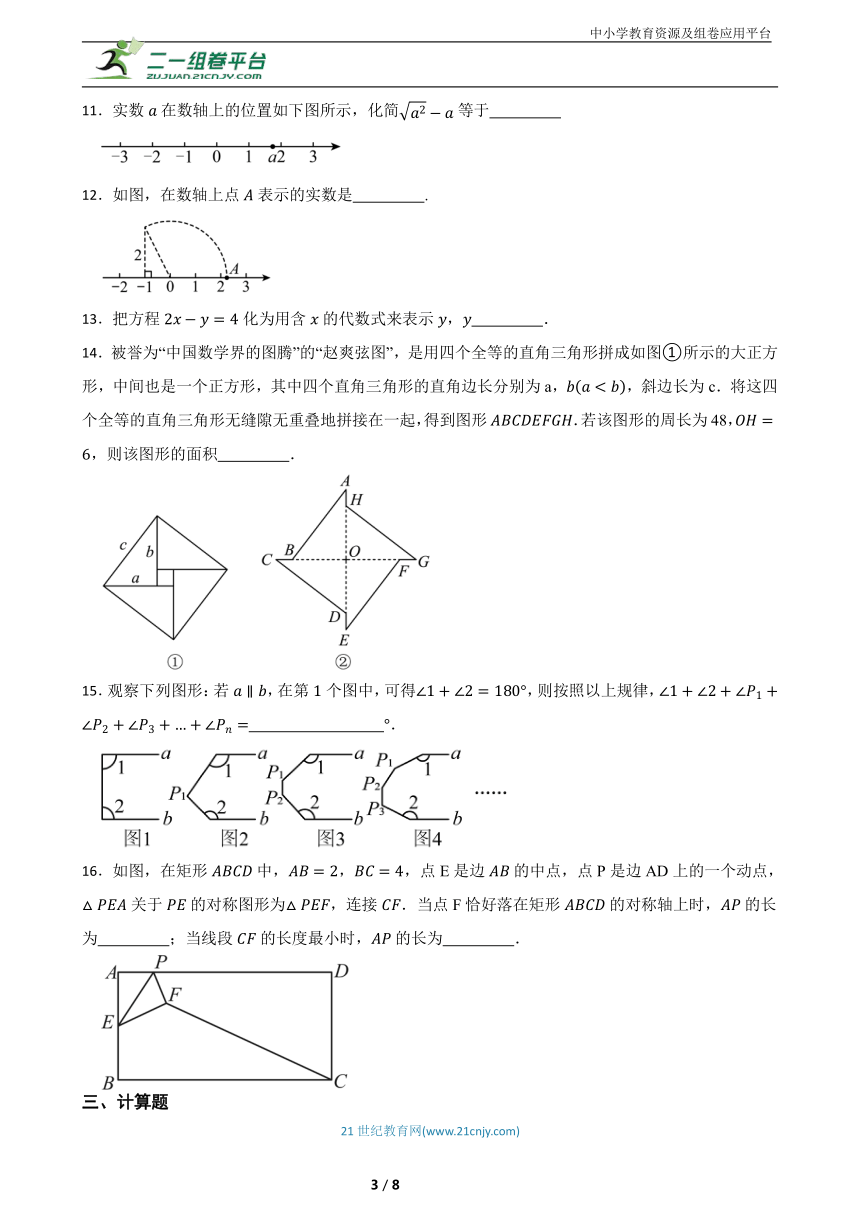
7.如图在矩形中,,,将沿对角线翻折,点落在点处,交于点,则的面积为( )
A. B. C.21 D.24
8.估计的运算结果应在哪两个整数之间( )
A.2和3 B.3和4 C.4和5 D.5和6
9.如图所示,下列条件中,能判断的是( )
A. B. C. D.
10.定义:如果代数式(,,,是常数)与(,,,是常数),满足,,,则称这两个代数式与互为“和谐式”,对于上述“和谐式”、,下列三个结论正确的个数为( )
①若,,则的值为-1;
②若为常数,关于的方程与的解相同,则;
③若,为常数,的最小值为,则有最小值,且最小值为1.
A.0个 B.1个 C.2个 D.3个
二、填空题
11.实数在数轴上的位置如下图所示,化简等于
12.如图,在数轴上点表示的实数是 .
13.把方程化为用含的代数式来表示, .
14.被誉为“中国数学界的图腾”的“赵爽弦图”,是用四个全等的直角三角形拼成如图①所示的大正方形,中间也是一个正方形,其中四个直角三角形的直角边长分别为a,,斜边长为c.将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形.若该图形的周长为48,,则该图形的面积 .
15.观察下列图形:若,在第个图中,可得,则按照以上规律, .
16.如图,在矩形中,,,点E是边的中点,点P是边AD上的一个动点,关于的对称图形为,连接.当点F恰好落在矩形的对称轴上时,的长为 ;当线段的长度最小时,的长为 .
三、计算题
17.解方程组.
18.计算
(1)
(2)
(3) x(2x+1) (2x+3)(1 x)
(4)(x+1)2﹣(x+2)(x-2)
19.如图,数轴上的点A、B、C、D、E表示连续的五个整数,对应数分别为a、b、c、d、e.
(1)若a+e=0,则代数式b+c+d= ;
(2)若a是最小的正整数,先化简,再求值:;
(3)若a+b+c+d=2,数轴上的点M表示的实数为m(m与a、b、c、d、e不同),且满足MA+MD=3,则m的范围是 .
四、解答题
20.如图,AB∥CD,∠A=38°,∠C=80°,求∠M.
21.如图,、分别为的高线和角平分线,,,求的度数.
22.如图所示,在四边形ABCD中,AB=2,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.
23.勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理. 在我国古书《周髀算经》中就有“若勾三,股四, 则弦五”的记载, 我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图” (如图 ①, 后人称之为 “赵爽弦图”, 流传至今.
(1) ①请叙述勾股定理.
②勾股定理的证明, 人们已经找到了 400 多种方法, 请从以下三种常见的证明方法中任选一种来证明该定理 (图 ①②③均满足证明勾股定理所需的条件).
(2) ①如图④⑤⑥, 以直角三角形的三边为边或直径, 分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足 的有 ▲ 个.
②如图⑦, 分别以直角三角形三边为直径作半圆, 设图中两个月牙形图案(图中阴影部分) 的面积分别为 , , 直角三角形的面积为 , 请判断 的数量关系并证明.
答案解析部分
1.【答案】A
【知识点】无理数的概念
2.【答案】B
【知识点】角平分线的性质;勾股定理
3.【答案】D
【知识点】中位数
4.【答案】C
【知识点】角的运算;余角、补角及其性质;平行线的性质
5.【答案】C
【知识点】二次根式的性质与化简
6.【答案】C
【知识点】点的坐标
7.【答案】A
【知识点】勾股定理;矩形的性质
8.【答案】C
【知识点】无理数的估值;二次根式的乘除法
9.【答案】D
【知识点】平行线的判定
10.【答案】C
【知识点】有理数的乘方法则;定义新运算;加减消元法解二元一次方程组
11.【答案】
【知识点】二次根式的性质与化简
12.【答案】
【知识点】无理数在数轴上表示
13.【答案】
【知识点】等式的基本性质;二元一次方程的概念
14.【答案】96
【知识点】勾股定理;“赵爽弦图”模型
15.【答案】
【知识点】平行线的性质;探索图形规律
16.【答案】1;
【知识点】勾股定理;矩形的性质
17.【答案】
【知识点】加减消元法解二元一次方程组
18.【答案】(1)解:
(2)解:
(3)解:
(4)解:
【知识点】实数的运算;整式的混合运算;零指数幂;负整数指数幂
19.【答案】(1)0;(2) ,;(3) ﹣1<x<2.
【知识点】无理数在数轴上表示
20.【答案】42°.
【知识点】三角形的外角性质
21.【答案】
【知识点】三角形的角平分线、中线和高;三角形内角和定理
22.【答案】四边形ABCD的面积是6.
【知识点】勾股定理的逆定理
23.【答案】(1)解:(1)①勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边为c,那么.
②选择图①,大正方形的面积等于四个全等三角形的面积与中间小正方形的面积之和,
即:
选择图②,大正方形的面积等于四个全等三角形的面积与中间小正方形的面积之和,
即:
化简得:
选择图③,梯形的面积等于三个直角三角形的面积之和,
即:
化简得:.
(2)3.
②∵
∴
∵
∴.
【知识点】勾股定理的证明;勾股定理的应用
21世纪教育网(www.21cnjy.com)
1 / 8
北师大版数学八年级上册期末复习题一
一、单选题
1.在0,,,,,,3.14,,相邻两个1之间0的个数逐次加1)中,无理数的个数有( )
A.2个 B.3个 C.4个 D.5个
2. 在长方形中,,,是边上一点,连接,把沿翻折,点恰好落在边上的处,延长,与的平分线交于点,交于点,则的长度为( )
A. B. C.4 D.
3.数据12,10,13,8,17,10,21的中位数是( )
A.8 B.10 C.13 D.12
4.如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=40°时,∠1的度数为( )
A.40° B.45° C.50° D.55°
5.化简的结果是( )
A. B. C. D.
6.在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点,第二次移动到点,…,第n次移动到点,则点的坐标是( )
A. B. C. D.
7.如图在矩形中,,,将沿对角线翻折,点落在点处,交于点,则的面积为( )
A. B. C.21 D.24
8.估计的运算结果应在哪两个整数之间( )
A.2和3 B.3和4 C.4和5 D.5和6
9.如图所示,下列条件中,能判断的是( )
A. B. C. D.
10.定义:如果代数式(,,,是常数)与(,,,是常数),满足,,,则称这两个代数式与互为“和谐式”,对于上述“和谐式”、,下列三个结论正确的个数为( )
①若,,则的值为-1;
②若为常数,关于的方程与的解相同,则;
③若,为常数,的最小值为,则有最小值,且最小值为1.
A.0个 B.1个 C.2个 D.3个
二、填空题
11.实数在数轴上的位置如下图所示,化简等于
12.如图,在数轴上点表示的实数是 .
13.把方程化为用含的代数式来表示, .
14.被誉为“中国数学界的图腾”的“赵爽弦图”,是用四个全等的直角三角形拼成如图①所示的大正方形,中间也是一个正方形,其中四个直角三角形的直角边长分别为a,,斜边长为c.将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形.若该图形的周长为48,,则该图形的面积 .
15.观察下列图形:若,在第个图中,可得,则按照以上规律, .
16.如图,在矩形中,,,点E是边的中点,点P是边AD上的一个动点,关于的对称图形为,连接.当点F恰好落在矩形的对称轴上时,的长为 ;当线段的长度最小时,的长为 .
三、计算题
17.解方程组.
18.计算
(1)
(2)
(3) x(2x+1) (2x+3)(1 x)
(4)(x+1)2﹣(x+2)(x-2)
19.如图,数轴上的点A、B、C、D、E表示连续的五个整数,对应数分别为a、b、c、d、e.
(1)若a+e=0,则代数式b+c+d= ;
(2)若a是最小的正整数,先化简,再求值:;
(3)若a+b+c+d=2,数轴上的点M表示的实数为m(m与a、b、c、d、e不同),且满足MA+MD=3,则m的范围是 .
四、解答题
20.如图,AB∥CD,∠A=38°,∠C=80°,求∠M.
21.如图,、分别为的高线和角平分线,,,求的度数.
22.如图所示,在四边形ABCD中,AB=2,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.
23.勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理. 在我国古书《周髀算经》中就有“若勾三,股四, 则弦五”的记载, 我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图” (如图 ①, 后人称之为 “赵爽弦图”, 流传至今.
(1) ①请叙述勾股定理.
②勾股定理的证明, 人们已经找到了 400 多种方法, 请从以下三种常见的证明方法中任选一种来证明该定理 (图 ①②③均满足证明勾股定理所需的条件).
(2) ①如图④⑤⑥, 以直角三角形的三边为边或直径, 分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足 的有 ▲ 个.
②如图⑦, 分别以直角三角形三边为直径作半圆, 设图中两个月牙形图案(图中阴影部分) 的面积分别为 , , 直角三角形的面积为 , 请判断 的数量关系并证明.
答案解析部分
1.【答案】A
【知识点】无理数的概念
2.【答案】B
【知识点】角平分线的性质;勾股定理
3.【答案】D
【知识点】中位数
4.【答案】C
【知识点】角的运算;余角、补角及其性质;平行线的性质
5.【答案】C
【知识点】二次根式的性质与化简
6.【答案】C
【知识点】点的坐标
7.【答案】A
【知识点】勾股定理;矩形的性质
8.【答案】C
【知识点】无理数的估值;二次根式的乘除法
9.【答案】D
【知识点】平行线的判定
10.【答案】C
【知识点】有理数的乘方法则;定义新运算;加减消元法解二元一次方程组
11.【答案】
【知识点】二次根式的性质与化简
12.【答案】
【知识点】无理数在数轴上表示
13.【答案】
【知识点】等式的基本性质;二元一次方程的概念
14.【答案】96
【知识点】勾股定理;“赵爽弦图”模型
15.【答案】
【知识点】平行线的性质;探索图形规律
16.【答案】1;
【知识点】勾股定理;矩形的性质
17.【答案】
【知识点】加减消元法解二元一次方程组
18.【答案】(1)解:
(2)解:
(3)解:
(4)解:
【知识点】实数的运算;整式的混合运算;零指数幂;负整数指数幂
19.【答案】(1)0;(2) ,;(3) ﹣1<x<2.
【知识点】无理数在数轴上表示
20.【答案】42°.
【知识点】三角形的外角性质
21.【答案】
【知识点】三角形的角平分线、中线和高;三角形内角和定理
22.【答案】四边形ABCD的面积是6.
【知识点】勾股定理的逆定理
23.【答案】(1)解:(1)①勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边为c,那么.
②选择图①,大正方形的面积等于四个全等三角形的面积与中间小正方形的面积之和,
即:
选择图②,大正方形的面积等于四个全等三角形的面积与中间小正方形的面积之和,
即:
化简得:
选择图③,梯形的面积等于三个直角三角形的面积之和,
即:
化简得:.
(2)3.
②∵
∴
∵
∴.
【知识点】勾股定理的证明;勾股定理的应用
21世纪教育网(www.21cnjy.com)
1 / 8
同课章节目录
