专题强化四 平衡中的临界极值问题 学案
文档属性
| 名称 | 专题强化四 平衡中的临界极值问题 学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-20 17:41:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
高中物理必修一素养提升学案
第三章 相互作用
专题强化四 平衡中的临界极值问题
【专题解读】
1.临界问题
(1)问题界定:物体所处平衡状态将要发生变化的状态为临界状态,涉及临界状态的问题为临界问题。
(2)问题特点
①当某物理量发生变化时,会引起其他几个物理量的变化。
②注意某现象“恰好出现”或“恰好不出现”的条件。
(3)处理方法:基本方法是假设推理法,即先假设某种情况成立,然后根据平衡条件及有关知识进行论证、求解。
2.极值问题
(1)问题界定:物体平衡的极值问题,一般指在力的变化过程中涉及力的最大值和最小值的问题。
(2)处理方法
①解析法:根据物体的平衡条件列出方程,在解方程时,采用数学知识求极值或者根据物理临界条件求极值。
②图解法:根据物体的平衡条件作出力的矢量图,画出平行四边形或者矢量三角形进行动态分析,确定最大值或最小值。
【典例剖析】
例1 一盏电灯重力为G,悬于天花板上的B点,在电线O处系一细线OA,使电线OB与竖直方向的夹角为β=30°,OA与水平方向成α角,如图所示。现保持O点位置不变,使α角由0°缓慢增加到90°,在此过程中( )
A.电线OB上的拉力逐渐减小
B.细线OA上的拉力先减小后增大
C.细线OA上拉力的最小值为G
D.细线OA上拉力的最小值为G
答案 ABC
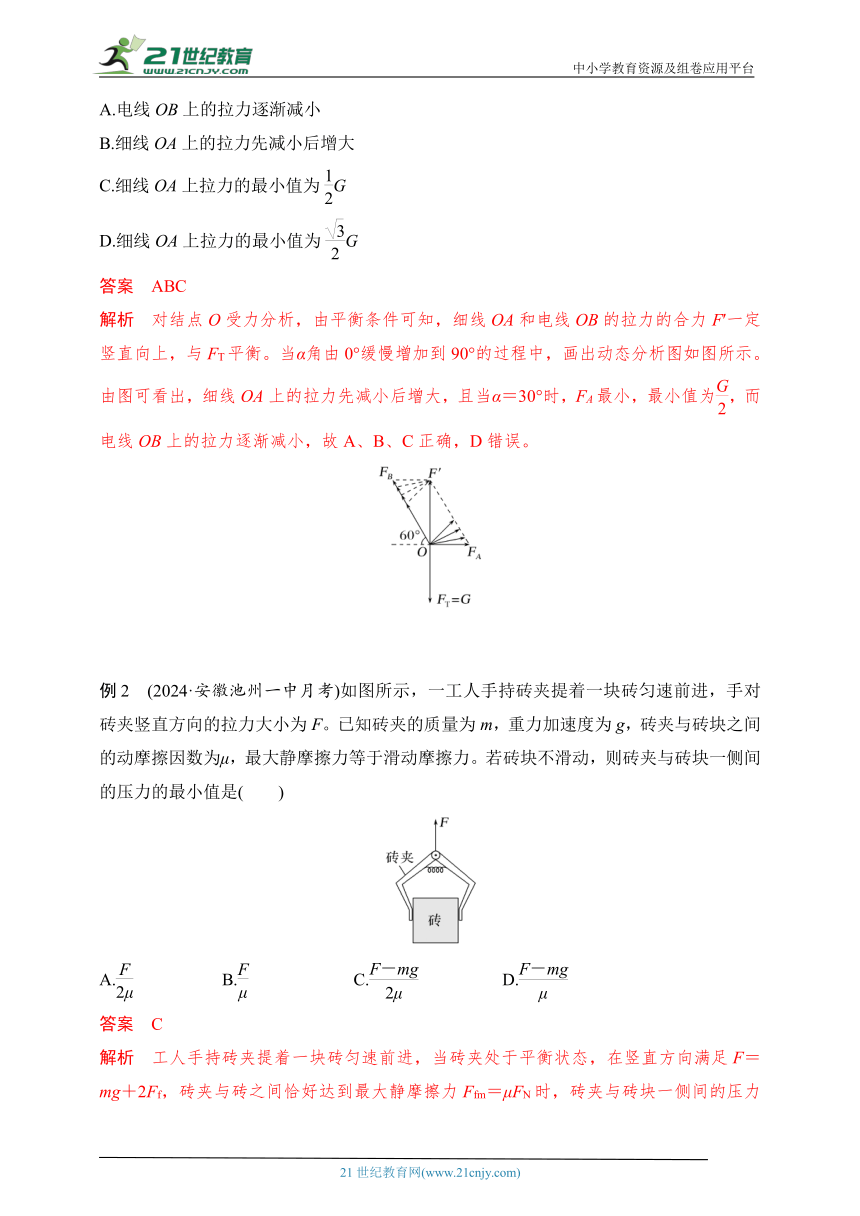
解析 对结点O受力分析,由平衡条件可知,细线OA和电线OB的拉力的合力F′一定竖直向上,与FT平衡。当α角由0°缓慢增加到90°的过程中,画出动态分析图如图所示。由图可看出,细线OA上的拉力先减小后增大,且当α=30°时,FA最小,最小值为,而电线OB上的拉力逐渐减小,故A、B、C正确,D错误。
例2 (2024·安徽池州一中月考)如图所示,一工人手持砖夹提着一块砖匀速前进,手对砖夹竖直方向的拉力大小为F。已知砖夹的质量为m,重力加速度为g,砖夹与砖块之间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力。若砖块不滑动,则砖夹与砖块一侧间的压力的最小值是( )
A. B. C. D.
答案 C
解析 工人手持砖夹提着一块砖匀速前进,当砖夹处于平衡状态,在竖直方向满足F=mg+2Ff,砖夹与砖之间恰好达到最大静摩擦力Ffm=μFN时,砖夹与砖块一侧间的压力的最小,为FNmin=,C项正确。
【针对性训练】
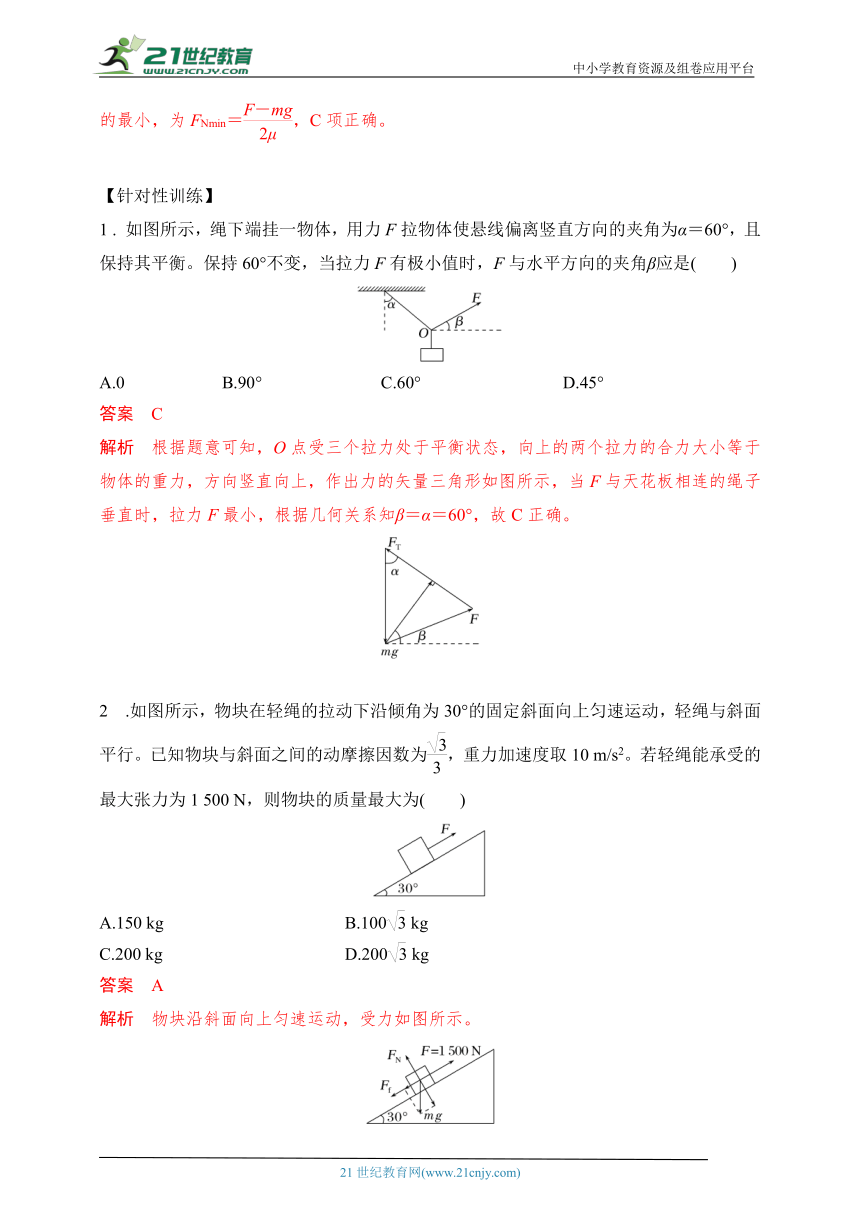
1 . 如图所示,绳下端挂一物体,用力F拉物体使悬线偏离竖直方向的夹角为α=60°,且保持其平衡。保持60°不变,当拉力F有极小值时,F与水平方向的夹角β应是( )
A.0 B.90° C.60° D.45°
答案 C
解析 根据题意可知,O点受三个拉力处于平衡状态,向上的两个拉力的合力大小等于物体的重力,方向竖直向上,作出力的矢量三角形如图所示,当F与天花板相连的绳子垂直时,拉力F最小,根据几何关系知β=α=60°,故C正确。
2 .如图所示,物块在轻绳的拉动下沿倾角为30°的固定斜面向上匀速运动,轻绳与斜面平行。已知物块与斜面之间的动摩擦因数为,重力加速度取10 m/s2。若轻绳能承受的最大张力为1 500 N,则物块的质量最大为( )
A.150 kg B.100 kg
C.200 kg D.200 kg
答案 A
解析 物块沿斜面向上匀速运动,受力如图所示。
根据平衡条件
F=Ff+mgsin 30°①
Ff=μFN②
FN=mgcos 30°③
由①②③式得
F=mgsin 30°+μmgcos 30°
所以m=,当F取1 500 N时,对应的m最大。代入数据得m=150 kg,故A正确。
3 .北方农村秋冬季节常用金属丝网围成圆柱形粮仓储存玉米棒,某粮仓由于玉米棒装的不匀称而发生倾斜现象,为避免倾倒,在左侧用木棍支撑,如图所示。若支撑点距水平地面的高度为 m,木棍与水平地面间的动摩擦因数为,木棍重力不计,粮仓对木棍的作用力沿木棍方向,最大静摩擦力等于滑动摩擦力,为使木棍下端一定不发生侧滑,则木棍的长度最多为( )
A.1.5 m B. m C.2 m D.2 m
答案 C
解析 设木棍与竖直方向夹角为θ,木棍长度为L,粮仓对木棍的作用力为F。为使木棍下端一定不发生侧滑,则有Fsin θ≤μFcos θ,即μ≥tan θ,由几何知识有tan θ=,联立解得L≤2 m,即木棍的长度最多为2 m,故C项正确。
4 .如图所示,一轻质光滑定滑轮固定在倾斜木板上,质量分别为m和2m的物块A、B,通过不可伸长的轻绳跨过滑轮连接,A、B间的接触面和轻绳均与木板平行.A与B间、B与木板间的动摩擦因数均为μ,设最大静摩擦力等于滑动摩擦力.当木板与水平面的夹角为45°时,物块A、B刚好要滑动,则μ的值为( C )
A. B. C. D.
答案 C
解析 根据题述,物块A、B刚要滑动,可知A、B之间的摩擦力fAB=μmgcos45°,B与木板之间的摩擦力f=μ·3mgcos45°.隔离A分析受力,由平衡条件可得轻绳中拉力F=fAB+mgsin45°.对AB整体,由平衡条件有2F=3mgsin45°-f,联立解得μ=,选项C正确.
5 .[2022浙江1月]如图所示,学校门口水平地面上有一质量为m的石礅,石礅与水平地面间的动摩擦因数为μ.工作人员用轻绳按图示方式匀速移动石礅时,两平行轻绳与水平面间的夹角均为θ,则下列说法正确的是( B )
A.轻绳的合拉力大小为
B.轻绳的合拉力大小为
C.减小夹角θ,轻绳的合拉力一定减小
D.轻绳的合拉力最小时,地面对石礅的摩擦力也最小
答案 B
解析 对石礅受力分析如图所示,设两根轻绳的合力为F,根据平衡条件有Fcosθ=f,Fsinθ+FN=mg,且μFN=f,联立可得F=,选项A错误,B正确;上式变形得F=,
其中tanα=,根据三角函数特点,由于θ的初始值不知道,因此减小θ,轻绳的合拉力F并不一定减小,选项C错误;根据上述讨论,当θ+α=90°时,轻绳的合拉力F最小,而摩擦力f=Fcosθ==,可知增大夹角θ,摩擦力一直减小,当θ趋近于90°时,摩擦力最小,故轻绳的合拉力F最小时,地面对石礅的摩擦力不是最小的,选项D错误.
6 . [2024吉林长春质量监测]如图,质量为m的光滑球体夹在竖直墙壁和斜面体之间,斜面体的质量为2m,倾角θ=37°,设斜面体与地面间的最大静摩擦力等于滑动摩擦力,若斜面体恰好不滑动,则斜面体与水平地面间的动摩擦因数μ为(sin37°=0.6,cos37°=0.8)( A )
A. B. C. D.
答案 A
解析 对光滑球体受力分析,如图1所示,则由平衡条件有N1=N2sinθ,mg=N2cosθ,联立解得N1=mg,对光滑球体与斜面体组成的整体受力分析,如图2所示,则由平衡条件有N1=μN3,3mg=N3,联立解得μ=,A正确.
7 如图所示为两个挡板夹一个小球的纵截面图,每个挡板和竖直方向的夹角均为θ.挡板与小球间的最大静摩擦力等于滑动摩擦力,小球静止不动.小球的质量为m,与两挡板之间的动摩擦因数均为μ(μ<tanθ),重力加速度为g.则每个挡板的弹力N的范围为多少?
答案 ≤N≤
解析 挡板对小球的弹力最小时,小球受到的摩擦力方向沿挡板向上,如图所示,小球受力平衡,由平衡条件得2Nminsinθ+2fmaxcosθ=mg,此时的最大静摩擦力fmax=μNmin,联立解得Nmin=;挡板对小球的弹力最大时,小球受到的摩擦力沿挡板向下,由平衡条件得2Nmaxsinθ=2f'maxcosθ+mg,此时的最大静摩擦力f'max=μNmax,联立解得Nmax=;则每个挡板弹力N的取值范围为≤N≤.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
高中物理必修一素养提升学案
第三章 相互作用
专题强化四 平衡中的临界极值问题
【专题解读】
1.临界问题
(1)问题界定:物体所处平衡状态将要发生变化的状态为临界状态,涉及临界状态的问题为临界问题。
(2)问题特点
①当某物理量发生变化时,会引起其他几个物理量的变化。
②注意某现象“恰好出现”或“恰好不出现”的条件。
(3)处理方法:基本方法是假设推理法,即先假设某种情况成立,然后根据平衡条件及有关知识进行论证、求解。
2.极值问题
(1)问题界定:物体平衡的极值问题,一般指在力的变化过程中涉及力的最大值和最小值的问题。
(2)处理方法
①解析法:根据物体的平衡条件列出方程,在解方程时,采用数学知识求极值或者根据物理临界条件求极值。
②图解法:根据物体的平衡条件作出力的矢量图,画出平行四边形或者矢量三角形进行动态分析,确定最大值或最小值。
【典例剖析】
例1 一盏电灯重力为G,悬于天花板上的B点,在电线O处系一细线OA,使电线OB与竖直方向的夹角为β=30°,OA与水平方向成α角,如图所示。现保持O点位置不变,使α角由0°缓慢增加到90°,在此过程中( )
A.电线OB上的拉力逐渐减小
B.细线OA上的拉力先减小后增大
C.细线OA上拉力的最小值为G
D.细线OA上拉力的最小值为G
答案 ABC
解析 对结点O受力分析,由平衡条件可知,细线OA和电线OB的拉力的合力F′一定竖直向上,与FT平衡。当α角由0°缓慢增加到90°的过程中,画出动态分析图如图所示。由图可看出,细线OA上的拉力先减小后增大,且当α=30°时,FA最小,最小值为,而电线OB上的拉力逐渐减小,故A、B、C正确,D错误。
例2 (2024·安徽池州一中月考)如图所示,一工人手持砖夹提着一块砖匀速前进,手对砖夹竖直方向的拉力大小为F。已知砖夹的质量为m,重力加速度为g,砖夹与砖块之间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力。若砖块不滑动,则砖夹与砖块一侧间的压力的最小值是( )
A. B. C. D.
答案 C
解析 工人手持砖夹提着一块砖匀速前进,当砖夹处于平衡状态,在竖直方向满足F=mg+2Ff,砖夹与砖之间恰好达到最大静摩擦力Ffm=μFN时,砖夹与砖块一侧间的压力的最小,为FNmin=,C项正确。
【针对性训练】
1 . 如图所示,绳下端挂一物体,用力F拉物体使悬线偏离竖直方向的夹角为α=60°,且保持其平衡。保持60°不变,当拉力F有极小值时,F与水平方向的夹角β应是( )
A.0 B.90° C.60° D.45°
答案 C
解析 根据题意可知,O点受三个拉力处于平衡状态,向上的两个拉力的合力大小等于物体的重力,方向竖直向上,作出力的矢量三角形如图所示,当F与天花板相连的绳子垂直时,拉力F最小,根据几何关系知β=α=60°,故C正确。
2 .如图所示,物块在轻绳的拉动下沿倾角为30°的固定斜面向上匀速运动,轻绳与斜面平行。已知物块与斜面之间的动摩擦因数为,重力加速度取10 m/s2。若轻绳能承受的最大张力为1 500 N,则物块的质量最大为( )
A.150 kg B.100 kg
C.200 kg D.200 kg
答案 A
解析 物块沿斜面向上匀速运动,受力如图所示。
根据平衡条件
F=Ff+mgsin 30°①
Ff=μFN②
FN=mgcos 30°③
由①②③式得
F=mgsin 30°+μmgcos 30°
所以m=,当F取1 500 N时,对应的m最大。代入数据得m=150 kg,故A正确。
3 .北方农村秋冬季节常用金属丝网围成圆柱形粮仓储存玉米棒,某粮仓由于玉米棒装的不匀称而发生倾斜现象,为避免倾倒,在左侧用木棍支撑,如图所示。若支撑点距水平地面的高度为 m,木棍与水平地面间的动摩擦因数为,木棍重力不计,粮仓对木棍的作用力沿木棍方向,最大静摩擦力等于滑动摩擦力,为使木棍下端一定不发生侧滑,则木棍的长度最多为( )
A.1.5 m B. m C.2 m D.2 m
答案 C
解析 设木棍与竖直方向夹角为θ,木棍长度为L,粮仓对木棍的作用力为F。为使木棍下端一定不发生侧滑,则有Fsin θ≤μFcos θ,即μ≥tan θ,由几何知识有tan θ=,联立解得L≤2 m,即木棍的长度最多为2 m,故C项正确。
4 .如图所示,一轻质光滑定滑轮固定在倾斜木板上,质量分别为m和2m的物块A、B,通过不可伸长的轻绳跨过滑轮连接,A、B间的接触面和轻绳均与木板平行.A与B间、B与木板间的动摩擦因数均为μ,设最大静摩擦力等于滑动摩擦力.当木板与水平面的夹角为45°时,物块A、B刚好要滑动,则μ的值为( C )
A. B. C. D.
答案 C
解析 根据题述,物块A、B刚要滑动,可知A、B之间的摩擦力fAB=μmgcos45°,B与木板之间的摩擦力f=μ·3mgcos45°.隔离A分析受力,由平衡条件可得轻绳中拉力F=fAB+mgsin45°.对AB整体,由平衡条件有2F=3mgsin45°-f,联立解得μ=,选项C正确.
5 .[2022浙江1月]如图所示,学校门口水平地面上有一质量为m的石礅,石礅与水平地面间的动摩擦因数为μ.工作人员用轻绳按图示方式匀速移动石礅时,两平行轻绳与水平面间的夹角均为θ,则下列说法正确的是( B )
A.轻绳的合拉力大小为
B.轻绳的合拉力大小为
C.减小夹角θ,轻绳的合拉力一定减小
D.轻绳的合拉力最小时,地面对石礅的摩擦力也最小
答案 B
解析 对石礅受力分析如图所示,设两根轻绳的合力为F,根据平衡条件有Fcosθ=f,Fsinθ+FN=mg,且μFN=f,联立可得F=,选项A错误,B正确;上式变形得F=,
其中tanα=,根据三角函数特点,由于θ的初始值不知道,因此减小θ,轻绳的合拉力F并不一定减小,选项C错误;根据上述讨论,当θ+α=90°时,轻绳的合拉力F最小,而摩擦力f=Fcosθ==,可知增大夹角θ,摩擦力一直减小,当θ趋近于90°时,摩擦力最小,故轻绳的合拉力F最小时,地面对石礅的摩擦力不是最小的,选项D错误.
6 . [2024吉林长春质量监测]如图,质量为m的光滑球体夹在竖直墙壁和斜面体之间,斜面体的质量为2m,倾角θ=37°,设斜面体与地面间的最大静摩擦力等于滑动摩擦力,若斜面体恰好不滑动,则斜面体与水平地面间的动摩擦因数μ为(sin37°=0.6,cos37°=0.8)( A )
A. B. C. D.
答案 A
解析 对光滑球体受力分析,如图1所示,则由平衡条件有N1=N2sinθ,mg=N2cosθ,联立解得N1=mg,对光滑球体与斜面体组成的整体受力分析,如图2所示,则由平衡条件有N1=μN3,3mg=N3,联立解得μ=,A正确.
7 如图所示为两个挡板夹一个小球的纵截面图,每个挡板和竖直方向的夹角均为θ.挡板与小球间的最大静摩擦力等于滑动摩擦力,小球静止不动.小球的质量为m,与两挡板之间的动摩擦因数均为μ(μ<tanθ),重力加速度为g.则每个挡板的弹力N的范围为多少?
答案 ≤N≤
解析 挡板对小球的弹力最小时,小球受到的摩擦力方向沿挡板向上,如图所示,小球受力平衡,由平衡条件得2Nminsinθ+2fmaxcosθ=mg,此时的最大静摩擦力fmax=μNmin,联立解得Nmin=;挡板对小球的弹力最大时,小球受到的摩擦力沿挡板向下,由平衡条件得2Nmaxsinθ=2f'maxcosθ+mg,此时的最大静摩擦力f'max=μNmax,联立解得Nmax=;则每个挡板弹力N的取值范围为≤N≤.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
