2024年北京五中高一(上)期中数学(PDF版,无答案)
文档属性
| 名称 | 2024年北京五中高一(上)期中数学(PDF版,无答案) |  | |
| 格式 | |||
| 文件大小 | 401.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 18:28:31 | ||
图片预览

文档简介
2024北京五中高一(上)期中
数 学
一、单选题(共 10小题,每小题 4分,共 40分)
1.已知集合 A = x x 0 , B = x x 3 ,则 A ( R B) =( )
A. (0,+ ) B. 0,+ ) C. ( ,3 D. (3,+ )
2.命题“ x Z , x 0 ”的否定是( )
A. x Z , x 0 B. x Z , x 0
C. x Z, x 0 D. x Z, x 0
3.已知 a b , c d ,则下面不等式一定成立的是( )
A. a + d b + c B. a + d b + c C. a d b c D. a d b c
4.“ x 1”是不等式 (x +1)(x 1) 0成立的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.已知定义在R 上的偶函数 f ( x)在 ( , 0 上是增函数,且 f ( 1) = 0, 则使 f (x) 0 的 x的范围是
( )
A. ( 1,0) B. (0,1) C. ( 1,1) D. ( , 1) (1,+ )
(a 3) x + 5, x 1
6.已知函数 f (x) = 2a 是 ( ,+ )上的减函数,则 a的取值范围是( )
, x 1
x
A. (0, 2) B. (0,2 C. (0,3) D. (0,3
7.如图所示,点 P 在边长为 1 的正方形的边上运动,设M 是CD边的中点,则当点 P 沿着 A B C M
运动时,以点 P 经过的路程 x为自变量,三角形 APM 的面积函数的图象形状大致是( )
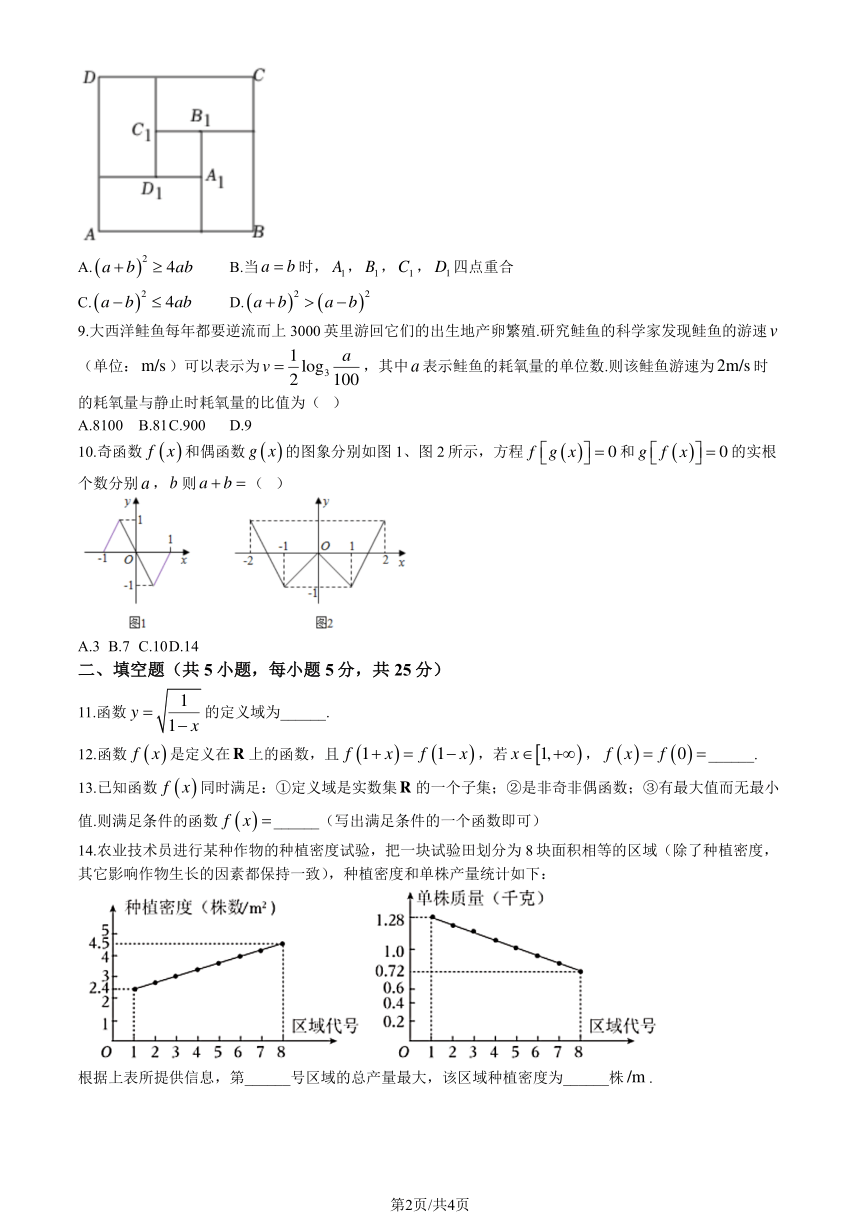
8.如图所示,4 个长为a,宽为b 的长方形拱成一个正方形 ABCD,中间围成一个小正方形 A1B1C1D1,则
下面说法错误的是( )
第1页/共4页
2
A. (a + b) 4ab B.当 a = b 时, A1, B1,C1 , D1 四点重合
2 2 2
C. (a b) 4ab D. (a +b) (a b)
9.大西洋鲑鱼每年都要逆流而上 3000 英里游回它们的出生地产卵繁殖.研究鲑鱼的科学家发现鲑鱼的游速v
1 a
(单位:m/s )可以表示为 v = log ,其中 a表示鲑鱼的耗氧量的单位数.则该鲑鱼游速为2m/s 时3
2 100
的耗氧量与静止时耗氧量的比值为( )
A.8100 B.81 C.900 D.9
10.奇函数 f ( x)和偶函数 g (x)的图象分别如图 1、图 2 所示,方程 f g (x) = 0 和 g f (x) = 0 的实根
个数分别 a,b 则 a + b =( )
A.3 B.7 C.10 D.14
二、填空题(共 5小题,每小题 5分,共 25分)
1
11.函数 y = 的定义域为______.
1 x
12.函数 f ( x)是定义在R 上的函数,且 f (1+ x) = f (1 x),若 x 1,+ ), f (x) = f (0) = ______.
13.已知函数 f ( x)同时满足:①定义域是实数集R 的一个子集;②是非奇非偶函数;③有最大值而无最小
值.则满足条件的函数 f ( x) = ______(写出满足条件的一个函数即可)
14.农业技术员进行某种作物的种植密度试验,把一块试验田划分为 8 块面积相等的区域(除了种植密度,
其它影响作物生长的因素都保持一致),种植密度和单株产量统计如下:
根据上表所提供信息,第______号区域的总产量最大,该区域种植密度为______株 /m .
第2页/共4页
2x 1
15.对于函数 f (x) = ,下列说法正确的是______.(写出所有正确命题的序号)
2x +1
( )
2 2
①函数 f x 为奇函数; ②函数 f ( x)的值域为 , ;
3 3
③函数在定义域上为增函数; ④对于 a R ,均有 f (a +1) f (a 1) .
三、解答题共 6小题,共 85分.解答应写出文字说明,演算步骤或证明过程.
16.(本小题 12 分)计算:
1
1 3 3
(Ⅰ) 6 + 3
3
+ 125 ;
4 8
(Ⅱ) log4 3 log9 2 log1 32 ;
2
3
2
0 16 4
(Ⅲ) 27 3
log
3 3
2
( 3 +1) .
81
17.(本小题 15 分)已知关于 x的不等式 (ax 1)(x 2) 2的解集为 A ,且3 A .
(Ⅰ)求实数 a的取值范围;
(Ⅱ)求集合 A .
x x x
18.(本小题 13 分)函数 f (x) = 4 + 2 + a , g (x) = 2 .
(Ⅰ)若 f ( x)过点 (0,3),求 a的值;
(Ⅱ)在(Ⅰ)的条件下,若 x 0,1 ,求 f ( x)的最大值;
(Ⅲ)若 y = f (x)图象恒在 y = g (x)图象的上方,求实数 a的取值范围.
ax2 +b 5
19.(本小题 15 分)已知函数 f (x) = ,且 f (1) = 2 , f (2) = .
x 2
(Ⅰ)确定函数 f ( x)的解析式,并判断奇偶性;
(Ⅱ)用定义证明函数 f ( x)在区间 ( , 1)上单调递增;
(Ⅲ)求满足 f (1+ 2t2 ) f (3+ t2 ) 0的实数 t 的取值范围.
20.(本小题 15 分)若函数 f ( x)对于其定义域内的某一数 x0 ,有 f (x0 ) = x0 ,则称 x f x0 是 ( )的一个不
f (x) = ax2动点.已知函数 + (b +1) x +b 1( a 0).
(Ⅰ)当 a =1,b = 2时,求函数 f ( x)的不动点;
(Ⅱ)若对任意的实数b ,函数 f ( x)恒有两个相异不动点,求 a的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若 y = f (x)图象上两个点 A 、 B 的横坐标是函数 f ( x)的不动点 A 、 B 的中
a
点C 在函数 g (x) = x + 的图象上,求b 的最值
5a2 4a +1
21.(本小题 15 分)设 A 是正整数集的非空子集,称集合 B = u v u,v A,且u v 为集合 A 的生成集.
(Ⅰ)当 A = 1,3,6 时,写出集合 A 的生成集 B ;
(Ⅱ)若 A 是由 5 个正整数构成的集合,求其生成集 B 中元素个数的最小值;
第3页/共4页
(Ⅲ)判断是否存在 4 个正整数构成的集合 A ,使其生成集 B = 2,3,5,6,10,16 ,并说明理由.
第4页/共4页
数 学
一、单选题(共 10小题,每小题 4分,共 40分)
1.已知集合 A = x x 0 , B = x x 3 ,则 A ( R B) =( )
A. (0,+ ) B. 0,+ ) C. ( ,3 D. (3,+ )
2.命题“ x Z , x 0 ”的否定是( )
A. x Z , x 0 B. x Z , x 0
C. x Z, x 0 D. x Z, x 0
3.已知 a b , c d ,则下面不等式一定成立的是( )
A. a + d b + c B. a + d b + c C. a d b c D. a d b c
4.“ x 1”是不等式 (x +1)(x 1) 0成立的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.已知定义在R 上的偶函数 f ( x)在 ( , 0 上是增函数,且 f ( 1) = 0, 则使 f (x) 0 的 x的范围是
( )
A. ( 1,0) B. (0,1) C. ( 1,1) D. ( , 1) (1,+ )
(a 3) x + 5, x 1
6.已知函数 f (x) = 2a 是 ( ,+ )上的减函数,则 a的取值范围是( )
, x 1
x
A. (0, 2) B. (0,2 C. (0,3) D. (0,3
7.如图所示,点 P 在边长为 1 的正方形的边上运动,设M 是CD边的中点,则当点 P 沿着 A B C M
运动时,以点 P 经过的路程 x为自变量,三角形 APM 的面积函数的图象形状大致是( )
8.如图所示,4 个长为a,宽为b 的长方形拱成一个正方形 ABCD,中间围成一个小正方形 A1B1C1D1,则
下面说法错误的是( )
第1页/共4页
2
A. (a + b) 4ab B.当 a = b 时, A1, B1,C1 , D1 四点重合
2 2 2
C. (a b) 4ab D. (a +b) (a b)
9.大西洋鲑鱼每年都要逆流而上 3000 英里游回它们的出生地产卵繁殖.研究鲑鱼的科学家发现鲑鱼的游速v
1 a
(单位:m/s )可以表示为 v = log ,其中 a表示鲑鱼的耗氧量的单位数.则该鲑鱼游速为2m/s 时3
2 100
的耗氧量与静止时耗氧量的比值为( )
A.8100 B.81 C.900 D.9
10.奇函数 f ( x)和偶函数 g (x)的图象分别如图 1、图 2 所示,方程 f g (x) = 0 和 g f (x) = 0 的实根
个数分别 a,b 则 a + b =( )
A.3 B.7 C.10 D.14
二、填空题(共 5小题,每小题 5分,共 25分)
1
11.函数 y = 的定义域为______.
1 x
12.函数 f ( x)是定义在R 上的函数,且 f (1+ x) = f (1 x),若 x 1,+ ), f (x) = f (0) = ______.
13.已知函数 f ( x)同时满足:①定义域是实数集R 的一个子集;②是非奇非偶函数;③有最大值而无最小
值.则满足条件的函数 f ( x) = ______(写出满足条件的一个函数即可)
14.农业技术员进行某种作物的种植密度试验,把一块试验田划分为 8 块面积相等的区域(除了种植密度,
其它影响作物生长的因素都保持一致),种植密度和单株产量统计如下:
根据上表所提供信息,第______号区域的总产量最大,该区域种植密度为______株 /m .
第2页/共4页
2x 1
15.对于函数 f (x) = ,下列说法正确的是______.(写出所有正确命题的序号)
2x +1
( )
2 2
①函数 f x 为奇函数; ②函数 f ( x)的值域为 , ;
3 3
③函数在定义域上为增函数; ④对于 a R ,均有 f (a +1) f (a 1) .
三、解答题共 6小题,共 85分.解答应写出文字说明,演算步骤或证明过程.
16.(本小题 12 分)计算:
1
1 3 3
(Ⅰ) 6 + 3
3
+ 125 ;
4 8
(Ⅱ) log4 3 log9 2 log1 32 ;
2
3
2
0 16 4
(Ⅲ) 27 3
log
3 3
2
( 3 +1) .
81
17.(本小题 15 分)已知关于 x的不等式 (ax 1)(x 2) 2的解集为 A ,且3 A .
(Ⅰ)求实数 a的取值范围;
(Ⅱ)求集合 A .
x x x
18.(本小题 13 分)函数 f (x) = 4 + 2 + a , g (x) = 2 .
(Ⅰ)若 f ( x)过点 (0,3),求 a的值;
(Ⅱ)在(Ⅰ)的条件下,若 x 0,1 ,求 f ( x)的最大值;
(Ⅲ)若 y = f (x)图象恒在 y = g (x)图象的上方,求实数 a的取值范围.
ax2 +b 5
19.(本小题 15 分)已知函数 f (x) = ,且 f (1) = 2 , f (2) = .
x 2
(Ⅰ)确定函数 f ( x)的解析式,并判断奇偶性;
(Ⅱ)用定义证明函数 f ( x)在区间 ( , 1)上单调递增;
(Ⅲ)求满足 f (1+ 2t2 ) f (3+ t2 ) 0的实数 t 的取值范围.
20.(本小题 15 分)若函数 f ( x)对于其定义域内的某一数 x0 ,有 f (x0 ) = x0 ,则称 x f x0 是 ( )的一个不
f (x) = ax2动点.已知函数 + (b +1) x +b 1( a 0).
(Ⅰ)当 a =1,b = 2时,求函数 f ( x)的不动点;
(Ⅱ)若对任意的实数b ,函数 f ( x)恒有两个相异不动点,求 a的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若 y = f (x)图象上两个点 A 、 B 的横坐标是函数 f ( x)的不动点 A 、 B 的中
a
点C 在函数 g (x) = x + 的图象上,求b 的最值
5a2 4a +1
21.(本小题 15 分)设 A 是正整数集的非空子集,称集合 B = u v u,v A,且u v 为集合 A 的生成集.
(Ⅰ)当 A = 1,3,6 时,写出集合 A 的生成集 B ;
(Ⅱ)若 A 是由 5 个正整数构成的集合,求其生成集 B 中元素个数的最小值;
第3页/共4页
(Ⅲ)判断是否存在 4 个正整数构成的集合 A ,使其生成集 B = 2,3,5,6,10,16 ,并说明理由.
第4页/共4页
同课章节目录
