第三章 勾股定理3 勾股定理的应用举例(含答案)
文档属性
| 名称 | 第三章 勾股定理3 勾股定理的应用举例(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 49.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-20 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
3 勾股定理的应用举例
1.如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到 B 处,现将圆柱侧面沿 “剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
2.如图,圆柱的高 BC 为 20 cm,底面周长是32 cm,一只蚂蚁从点 A 爬到点 P 处吃食, 且 则最短路线长为 ( )
A.20 cm B.13 cm C.14 cm D.18 cm
第2题图 第3题图
3.如图,在高为3米,斜坡长为5 米的楼梯台阶上铺地毯,则地毯的长度至少要 ( )
A. 5米 B. 6米 C. 7米 D. 8米
4.如图1,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根 12米处,图2是这棵大树折断的示意图,则这棵大树在折断之前的高是 ( )
A. 20米 B. 18米 C. 16米 D. 15米
5.如图, ,则加固小树的木棒DE的长是( )
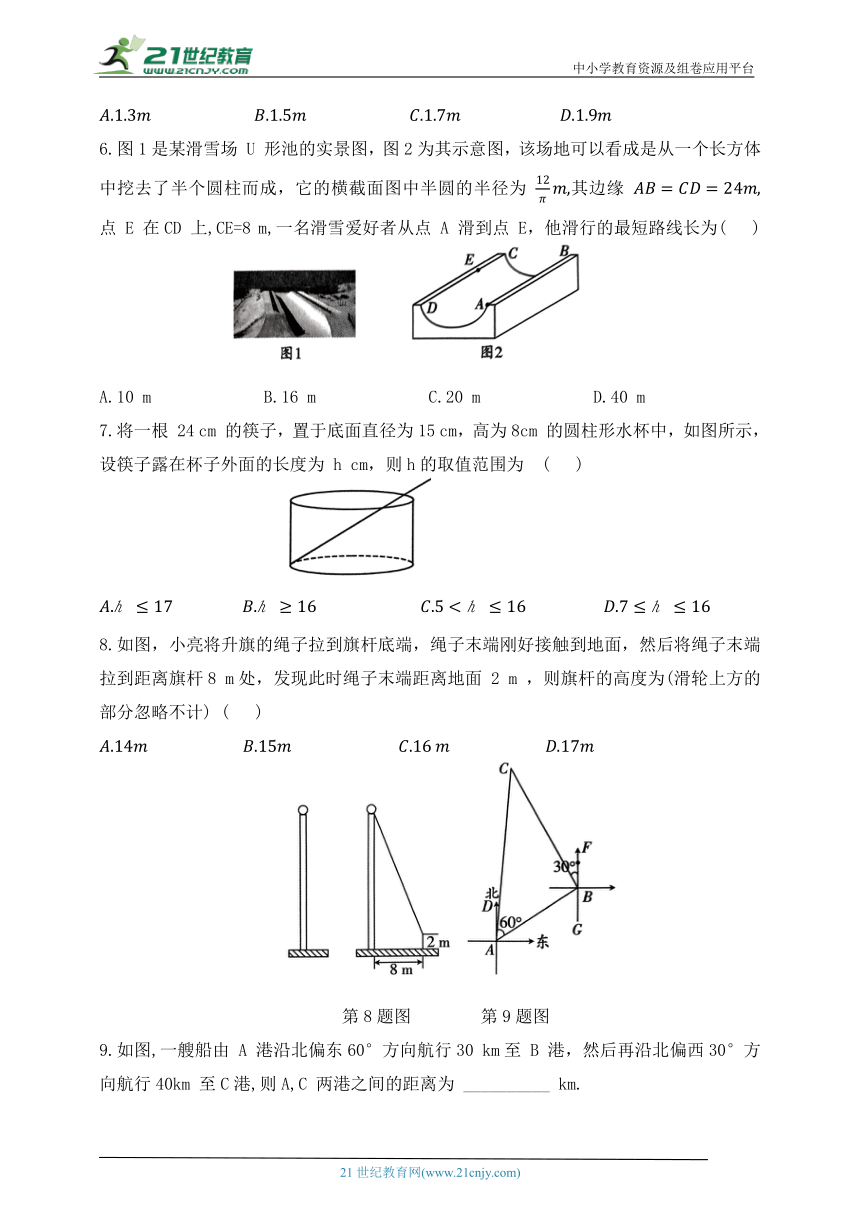
6.图1是某滑雪场 U 形池的实景图,图2为其示意图,该场地可以看成是从一个长方体中挖去了半个圆柱而成,它的横截面图中半圆的半径为 其边缘 点 E 在CD 上,CE=8 m,一名滑雪爱好者从点 A 滑到点 E,他滑行的最短路线长为( )
A.10 m B.16 m C.20 m D.40 m
7.将一根 24 cm 的筷子,置于底面直径为15 cm,高为8cm 的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为 h cm,则h的取值范围为 ( )
8.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面 2 m ,则旗杆的高度为(滑轮上方的部分忽略不计) ( )
第8题图 第9题图
9.如图,一艘船由 A 港沿北偏东60°方向航行30 km至 B 港,然后再沿北偏西30°方向航行40km 至C港,则A,C 两港之间的距离为 __________ km.
10.笔直的河流一侧有一旅游地C,河边有两个漂流点 A,B.其中 由于某种原因,由C到 A 的路现在已经不通,为方便游客,景区决定在河边新建一个漂流点 H(A,H,B在同一直线上),并新修一条路CH,测得 5千米, 千米, 千米,则原路线 千米.
11.如图是一个底面为等边三角形的三棱镜,在三棱镜的侧面上,从顶点 A 到顶点. 镶有一圈金属丝,已知此三棱镜的高为5cm,底面边长为4 cm,则这圈金属丝的长度至少为______________.
12.如图所示,ABCD 是长方形地面,长 宽 中间竖有一堵砖墙高 一只蚂蚱从 A 点爬到 C 点,它必须翻过中间那堵墙,则它至少要走_______ m的路程.
13.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子 BC 的长为17米,几分钟后船到达点 D 的位置,此时绳子CD的长为10米,问船向岸边移动了_________米.
14.如图,小明在广场上先向东走10m,又向南走40m,再向西走20 m,又向南走40m,再向东走70 m.则小明到达的终点与出发点的直线距离是____________.
第14 题图 第15 题图
15.如图所示,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点 A 爬到点 B,需要爬行的最短距离是___________.
16.如图,一牧童在 A 处牧马,牧童的家在B处,A,B处相距河岸的距离分别是 且C,D两地间的距离也为500m, 天黑前牧童从 A 点将马牵到河边去饮水,再赶回家.
(1)为了使所走的路程最短,牧童应将马赶到河边什么地点 请你在图中画出来并描述画图的主要步骤;
(2)请你求出他至少要走多少路程.
17.如图,圆柱形玻璃杯的杯高为 9 cm,底面周长为16 cm,在杯内壁离杯底4 cm的点 A 处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿 1 cm,且与蜂蜜相对的点 B 处,则蚂蚁从外壁 B 处到内壁A处所走的最短路程为___________ cm.(杯壁厚度不计)
18.有一个如图所示的长方体的透明鱼缸,假设其长 AD=80cm,高AB=60cm,水深AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm.一小虫想从鱼缸外的点 A 处沿缸壁爬到鱼缸内的G处吃鱼饵.
(1)小虫应该走怎样的路线才可使爬行的路程最短 请画出它的爬行路线的示意图,并用箭头标注;
(2)试求小虫爬行的最短路程.
19.为了缓解司机的视力疲劳,某隧道施工单位准备在双向道路中间全程增加一个宽为1米的绿草坪.已知隧道截面是一个半径为4 米的半圆形,点O 是其圆心,AE 是绿草坪的截面.问一辆高3米,宽1.9米的卡车能通过这个隧道吗 请说明理由.
参考答案
1. C 2. A 3. C 4. B 5. C
6. C 解析:如图,由题意可得,12(m),
在 中, 所以 即他滑行的
最短路线长为20 m.
7. D 解析:如图1 所示,当筷子的底端在 D 点时,筷子露在杯子外面的长度最长,
所以
如图2所示,当筷子的底端在 A 点时,筷子露在杯子外面的长度最短,
在 中, 所以
所以 所以此时
所以h的取值范围是
8. D
9.50 解析:由题意,得. ∥
所以
所以
在 Rt△ABC中,AB=30 km,BC=40 km,
所以A,C两港之间的距离为50 km.
11.13 cm 12.26 13. 9 14.100m 15. 25
16.解:(1)如图1,作A点关于河岸CD 的对称点A',连接 交河岸于点 P,
则 最短,故牧童应将马赶到河边的 P 点;
(2)如图2,作 交 BD的延长线于点 则 CD, 所以 ∥所以
在 中,则
所以 所以
所以他至少要走1 300 m路程.
17.10 解析:如图:
将杯子侧面展开,作点 B 关于 EF 的对称点连接 则 即为最短距离,
由图可知,
由勾股定理得
18.解:(1)如图所示, AQ→QG为最短路线,
(2)因为 所以
因为 所以
所以 所以
所以小虫爬行的最短路程为100 cm.
19.解:这个卡车能通过这个隧道.
理由:设AB 表示车宽,那么. 米.
由题意,得 (米), (米).
在 中,因为 所以
所以
因为卡车高3米, 所以这个卡车能通过这个隧道.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 勾股定理
3 勾股定理的应用举例
1.如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到 B 处,现将圆柱侧面沿 “剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
2.如图,圆柱的高 BC 为 20 cm,底面周长是32 cm,一只蚂蚁从点 A 爬到点 P 处吃食, 且 则最短路线长为 ( )
A.20 cm B.13 cm C.14 cm D.18 cm
第2题图 第3题图
3.如图,在高为3米,斜坡长为5 米的楼梯台阶上铺地毯,则地毯的长度至少要 ( )
A. 5米 B. 6米 C. 7米 D. 8米
4.如图1,一棵大树在一次强烈的地震中于离地面5米处折断倒下,树顶落在离树根 12米处,图2是这棵大树折断的示意图,则这棵大树在折断之前的高是 ( )
A. 20米 B. 18米 C. 16米 D. 15米
5.如图, ,则加固小树的木棒DE的长是( )
6.图1是某滑雪场 U 形池的实景图,图2为其示意图,该场地可以看成是从一个长方体中挖去了半个圆柱而成,它的横截面图中半圆的半径为 其边缘 点 E 在CD 上,CE=8 m,一名滑雪爱好者从点 A 滑到点 E,他滑行的最短路线长为( )
A.10 m B.16 m C.20 m D.40 m
7.将一根 24 cm 的筷子,置于底面直径为15 cm,高为8cm 的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为 h cm,则h的取值范围为 ( )
8.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面 2 m ,则旗杆的高度为(滑轮上方的部分忽略不计) ( )
第8题图 第9题图
9.如图,一艘船由 A 港沿北偏东60°方向航行30 km至 B 港,然后再沿北偏西30°方向航行40km 至C港,则A,C 两港之间的距离为 __________ km.
10.笔直的河流一侧有一旅游地C,河边有两个漂流点 A,B.其中 由于某种原因,由C到 A 的路现在已经不通,为方便游客,景区决定在河边新建一个漂流点 H(A,H,B在同一直线上),并新修一条路CH,测得 5千米, 千米, 千米,则原路线 千米.
11.如图是一个底面为等边三角形的三棱镜,在三棱镜的侧面上,从顶点 A 到顶点. 镶有一圈金属丝,已知此三棱镜的高为5cm,底面边长为4 cm,则这圈金属丝的长度至少为______________.
12.如图所示,ABCD 是长方形地面,长 宽 中间竖有一堵砖墙高 一只蚂蚱从 A 点爬到 C 点,它必须翻过中间那堵墙,则它至少要走_______ m的路程.
13.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子 BC 的长为17米,几分钟后船到达点 D 的位置,此时绳子CD的长为10米,问船向岸边移动了_________米.
14.如图,小明在广场上先向东走10m,又向南走40m,再向西走20 m,又向南走40m,再向东走70 m.则小明到达的终点与出发点的直线距离是____________.
第14 题图 第15 题图
15.如图所示,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点 A 爬到点 B,需要爬行的最短距离是___________.
16.如图,一牧童在 A 处牧马,牧童的家在B处,A,B处相距河岸的距离分别是 且C,D两地间的距离也为500m, 天黑前牧童从 A 点将马牵到河边去饮水,再赶回家.
(1)为了使所走的路程最短,牧童应将马赶到河边什么地点 请你在图中画出来并描述画图的主要步骤;
(2)请你求出他至少要走多少路程.
17.如图,圆柱形玻璃杯的杯高为 9 cm,底面周长为16 cm,在杯内壁离杯底4 cm的点 A 处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿 1 cm,且与蜂蜜相对的点 B 处,则蚂蚁从外壁 B 处到内壁A处所走的最短路程为___________ cm.(杯壁厚度不计)
18.有一个如图所示的长方体的透明鱼缸,假设其长 AD=80cm,高AB=60cm,水深AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm.一小虫想从鱼缸外的点 A 处沿缸壁爬到鱼缸内的G处吃鱼饵.
(1)小虫应该走怎样的路线才可使爬行的路程最短 请画出它的爬行路线的示意图,并用箭头标注;
(2)试求小虫爬行的最短路程.
19.为了缓解司机的视力疲劳,某隧道施工单位准备在双向道路中间全程增加一个宽为1米的绿草坪.已知隧道截面是一个半径为4 米的半圆形,点O 是其圆心,AE 是绿草坪的截面.问一辆高3米,宽1.9米的卡车能通过这个隧道吗 请说明理由.
参考答案
1. C 2. A 3. C 4. B 5. C
6. C 解析:如图,由题意可得,12(m),
在 中, 所以 即他滑行的
最短路线长为20 m.
7. D 解析:如图1 所示,当筷子的底端在 D 点时,筷子露在杯子外面的长度最长,
所以
如图2所示,当筷子的底端在 A 点时,筷子露在杯子外面的长度最短,
在 中, 所以
所以 所以此时
所以h的取值范围是
8. D
9.50 解析:由题意,得. ∥
所以
所以
在 Rt△ABC中,AB=30 km,BC=40 km,
所以A,C两港之间的距离为50 km.
11.13 cm 12.26 13. 9 14.100m 15. 25
16.解:(1)如图1,作A点关于河岸CD 的对称点A',连接 交河岸于点 P,
则 最短,故牧童应将马赶到河边的 P 点;
(2)如图2,作 交 BD的延长线于点 则 CD, 所以 ∥所以
在 中,则
所以 所以
所以他至少要走1 300 m路程.
17.10 解析:如图:
将杯子侧面展开,作点 B 关于 EF 的对称点连接 则 即为最短距离,
由图可知,
由勾股定理得
18.解:(1)如图所示, AQ→QG为最短路线,
(2)因为 所以
因为 所以
所以 所以
所以小虫爬行的最短路程为100 cm.
19.解:这个卡车能通过这个隧道.
理由:设AB 表示车宽,那么. 米.
由题意,得 (米), (米).
在 中,因为 所以
所以
因为卡车高3米, 所以这个卡车能通过这个隧道.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
