2024-2025学年北京市顺义区十一学校顺义学校杨镇一中高二上学期期中考试数学试题(含答案)
文档属性
| 名称 | 2024-2025学年北京市顺义区十一学校顺义学校杨镇一中高二上学期期中考试数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 719.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-21 00:00:00 | ||
图片预览



文档简介
北京市十一学校顺义学校杨镇一中2024-2025学年高二上学期期中考试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.直线斜率的倾斜角是 ( )
A. B. C. D.
2.已知向量,则( )
A. B. C. D.
3.经过点且与直线平行的直线方程为 ( )
A. B.
C. D.
4.如图是某班50名学生期中考试物理成绩的频率分布直方图,其中成绩分组区间是,,,,,,则图中的值等于( ).
A. B. C. D.
5.甲、乙两个气象站同时作气象预报,如果甲站、乙站预报的准确率分别为和,那么在一次预报中两站恰有一次准确预报的概率为( )
A. B. C. D.
6.从甲乙丙三人中任选两名代表,甲被选中的概率为( )
A. B. C. D.
7.某赛季甲、乙两名篮球运动员各6场比赛得分情况记录如下,甲:18,20,35,33,47,41; 乙:17,26,19,27,19,29.则下列四个结论中,正确的是( )
A.甲运动员得分的极差小于乙运动员得分的极差
B.甲运动员得分的中位数小于乙运动员得分的中位数
C.甲运动员的成绩比乙运动员的成绩稳定
D.甲运动员得分的平均值大于乙运动员得分的平均值
8.已知平面的一个法向量为,且,则点A到平面的距离为( )
A. B. C. D.1
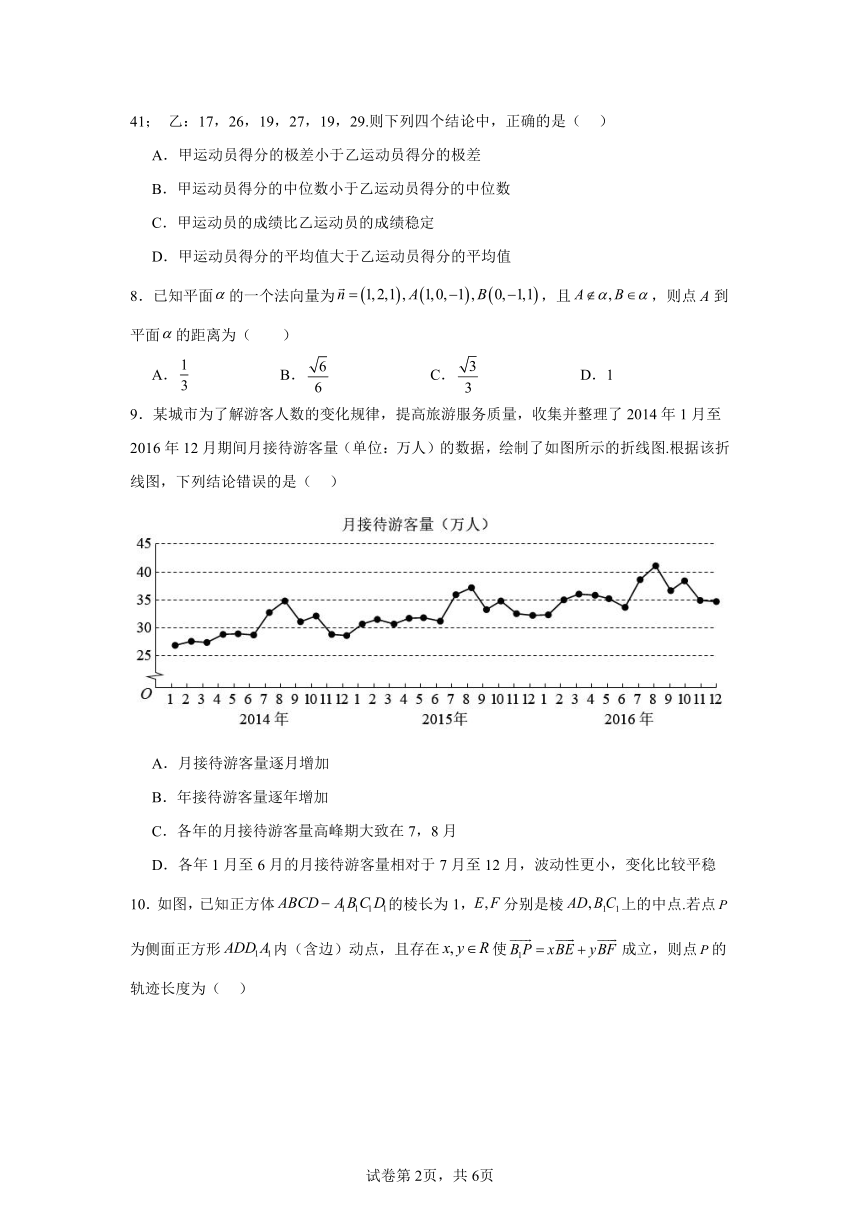
9.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
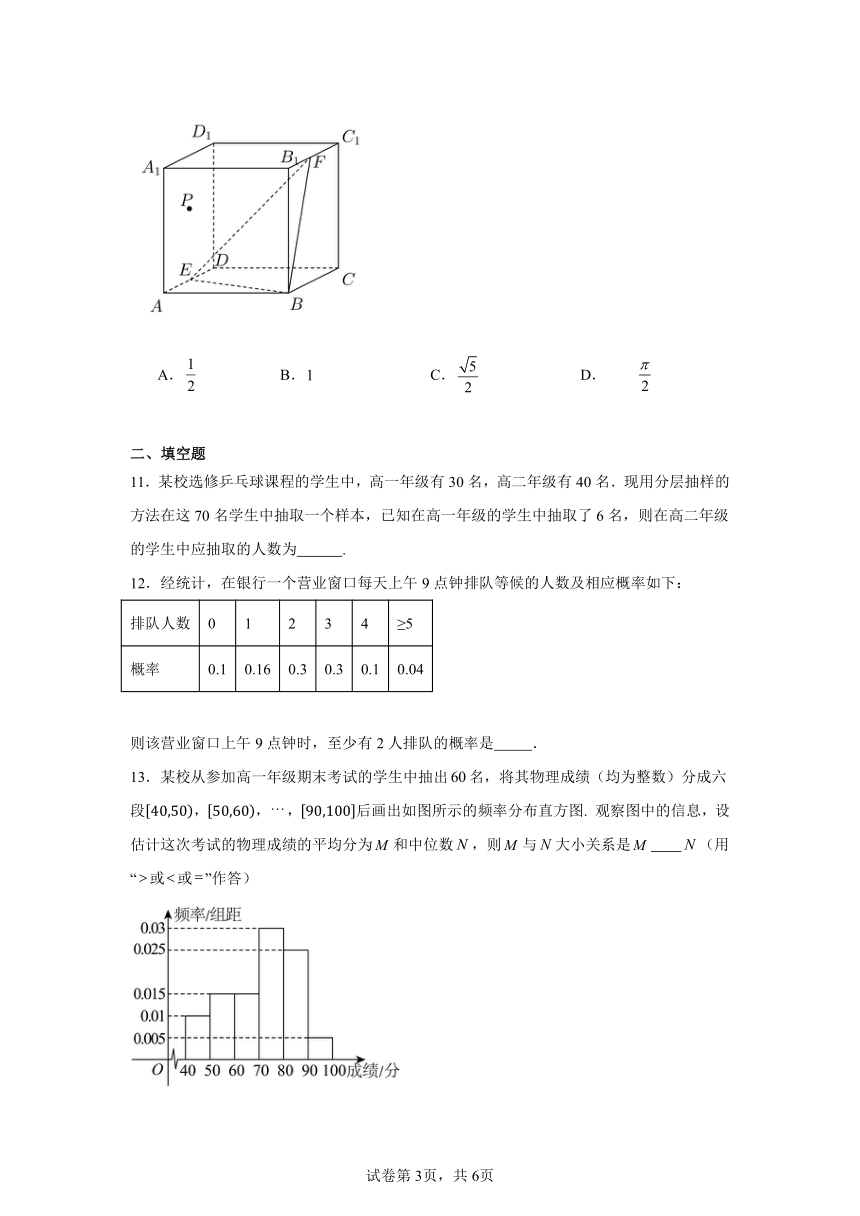
10.如图,已知正方体的棱长为1,分别是棱上的中点.若点为侧面正方形内(含边)动点,且存在使成立,则点的轨迹长度为( )
A. B. C. D.
二、填空题
11.某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为 .
12.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下:
排队人数 0 1 2 3 4 ≥5
概率 0.1 0.16 0.3 0.3 0.1 0.04
则该营业窗口上午9点钟时,至少有2人排队的概率是 .
13.某校从参加高一年级期末考试的学生中抽出名,将其物理成绩(均为整数)分成六段,,,后画出如图所示的频率分布直方图. 观察图中的信息,设估计这次考试的物理成绩的平均分为和中位数,则与大小关系是 (用“或或”作答)
14.已知直线过点,且和直线平行.设直线与轴相交于点,求直线绕点逆时针旋转所得直线的方程 .
15.如图,在长方体中,,,点在侧面上.若点到直线和的距离相等,则的最小值是 .
三、解答题
16.从2名男生(记为和)和3名女生(记为和)组成的总体中,任意依次抽取2名学生.
(1)不放回简单随机抽样求出抽到的2人为1名男生和1名女生的概率.
(2)有放回简单随机抽样求出抽到的2人为1名男生和1名女生的概率.
17.已知△ABC的三个顶点A(3,7),B(–2,5),C(–3,–5),点D为AC的中点.
(1)求点D的坐标;
(2)求直线BD的方程.
(3)求△ABD的面积.
18.如图,在四棱锥中,底面是正方形,侧棱底面,.
(1)求直线与直线所成角;
(2)求平面与平面的夹角.
19.2020年是我国网络建设的加速之年.截至2020年底,中国已建成全球最大的网络.为了切实推动移动网络质量提升,不断改善用户体验,中国信通院受工信部委托,定期在全国范围内开展重点场所移动网络质量专项测评.其中一项测评内容是在每座受测城市中挑选一条典型路段,以评估当地网络发展水平.其中5座受测城市的综合下载速率(单位:)数据如下表:
城市 路段 综合下载速率(单位:)
福州 五四路 708.92
广州 大学城外/中/内环 817.13
哈尔滨 红军街 630.34
杭州 环城东路 882.60
成都 二环高架 916.02
(1)从以上5座城市中随机选取2座城市进行分析,求选取的2座城市“综合下载速率”都大于800的概率;
(2)甲 乙两家网络运营商分别从以上5座城市中随机选取1座城市考察(甲 乙的选取互不影响),求甲 乙两家运营商中恰有1家选取的城市“综合下载速率”大于800的概率.
20.如图,四棱锥中,是以为斜边的等腰直角三角形,,,为的中点.
(1)求直线与平面所成角的正弦值;
(2)设是线段上一点,如果点是在平面内,判断点在线段的位置并证明你的结论;
(3)点在线段上运动,求点到直线的距离最大值.
21.我们知道,在平面中,给定一点和一条直线的法向量可以唯一确定一条直线. 如点在直线上,为直线的一个法向量,则直线上任意一点满足,则,化简可得,即为直线的方程. 类似的,在空间中,给定一点和一个平面的法向量可以唯一确定一个平面.
(1)若在空间直角坐标系中,,请利用平面的法向量求出平面的方程;
(2)试写出平面(不同时为0)的一个法向量(无需证明),并求出点到平面的距离.
试卷第1页,共3页
试卷第1页,共3页
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B D D C D B A C
11.8
12.0.74
13.
14.
15.
16.(1)从5名学生中,不放回地任意依次抽取2名学生的所有可能结果为:
,
共20种结果.
设事件为抽到的2人为1名男生和1名女生,则事件发生的所有可能结果为:
,共12种结果.
由古典概型的概率计算公式得:,
即不放回简单随机抽样求出抽到的2人为1名男生和1名女生的概率为.
(2)有放回简单随机抽样抽取2名学生的所有可能结果为:
,共25种结果.
设事件为抽到的2人为1名男生和1名女生,则事件发生的所有可能结果为:
,共12种结果.
由古典概型的概率计算公式得:,
即有放回简单随机抽样求出抽到的2人为1名男生和1名女生的概率为.
17.(1)设D(x,y),
则,,
∴点D的坐标为(0,1).
(2)∵直线BD的斜率为.
∴直线BD的方程为:y–1=–2(x–0),即2x+y–1=0.
(3)∵,
∴A到直线BD的距离为.
∴△ABD的面积为.
18.(1)底面,平面,,
则直线与直线所成的角为.
(2)由题意,底面是正方形,侧棱底面,
则以点为坐标原点,建立如图所示空间直角坐标系,
则,,,,
所以,,,
设平面的一个法向量为,
则,令则,
设平面的一个法向量为,
则,令,则,
则,
又平面与平面的夹角为锐角,
所以平面与平面的夹角为.
19.解:(1)5座城市中“综合下载速率”大于800Mbps的有3座,设为,
“综合下载速率”不大于800的有2座,设为.
随机选取2座城市所有可能为:,,,,,,,,,共10种.
其中2座城市“综合下载速率”都大于800的有,,共3种.
设两个城市“综合下载速率”都大于800为事件,
所以
(2)设甲选取的城市“综合下载速率”大于800为事件,乙选取的城市“综合下载速率”大于800为事件,恰有1家运营商选取的城市“综合下载速率”大于800为事件.
依题意,事件,
所以
.
20.(1)直角梯形中,由已知可得,,
∴,即,
又是以为斜边的等腰直角三角形,∴,
取中点,连接,则,,
则,∴,
又,∴,
∴,,而,平面,
∴平面,
因此可以为轴,过平行于的直线为轴建立空间直角坐标系,如图,
则,,,,,
,,
设平面的一个法向量为,
则,取,则,即,
又,
,
直线PB与平面PAC所成角为,则.
(2)是的中点,证明如下:
,,,,为的中点,
所以,设,
则,
若点是在平面内,则,
则,解得,所以是的中点.
(3)设,,,,
,,
所以点到直线的距离为
,所以点到直线的距离最大值为.
21.(1)在平面中,,
设平面的法向量为,
所以,即,令,则,
所以.
设平面内任意一点,则.
所以,化简得.
所以平面的方程为.
(2)平面的法向量可取.
证明如下:
设为平面的任意两个点,
则,,
两式相减得,
即,即,
所以平面的法向量可取.
因为A,B,C不同时为0,所以不妨令,
平面上可取点,
所以,
则点H到平面的距离.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.直线斜率的倾斜角是 ( )
A. B. C. D.
2.已知向量,则( )
A. B. C. D.
3.经过点且与直线平行的直线方程为 ( )
A. B.
C. D.
4.如图是某班50名学生期中考试物理成绩的频率分布直方图,其中成绩分组区间是,,,,,,则图中的值等于( ).
A. B. C. D.
5.甲、乙两个气象站同时作气象预报,如果甲站、乙站预报的准确率分别为和,那么在一次预报中两站恰有一次准确预报的概率为( )
A. B. C. D.
6.从甲乙丙三人中任选两名代表,甲被选中的概率为( )
A. B. C. D.
7.某赛季甲、乙两名篮球运动员各6场比赛得分情况记录如下,甲:18,20,35,33,47,41; 乙:17,26,19,27,19,29.则下列四个结论中,正确的是( )
A.甲运动员得分的极差小于乙运动员得分的极差
B.甲运动员得分的中位数小于乙运动员得分的中位数
C.甲运动员的成绩比乙运动员的成绩稳定
D.甲运动员得分的平均值大于乙运动员得分的平均值
8.已知平面的一个法向量为,且,则点A到平面的距离为( )
A. B. C. D.1
9.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
10.如图,已知正方体的棱长为1,分别是棱上的中点.若点为侧面正方形内(含边)动点,且存在使成立,则点的轨迹长度为( )
A. B. C. D.
二、填空题
11.某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为 .
12.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下:
排队人数 0 1 2 3 4 ≥5
概率 0.1 0.16 0.3 0.3 0.1 0.04
则该营业窗口上午9点钟时,至少有2人排队的概率是 .
13.某校从参加高一年级期末考试的学生中抽出名,将其物理成绩(均为整数)分成六段,,,后画出如图所示的频率分布直方图. 观察图中的信息,设估计这次考试的物理成绩的平均分为和中位数,则与大小关系是 (用“或或”作答)
14.已知直线过点,且和直线平行.设直线与轴相交于点,求直线绕点逆时针旋转所得直线的方程 .
15.如图,在长方体中,,,点在侧面上.若点到直线和的距离相等,则的最小值是 .
三、解答题
16.从2名男生(记为和)和3名女生(记为和)组成的总体中,任意依次抽取2名学生.
(1)不放回简单随机抽样求出抽到的2人为1名男生和1名女生的概率.
(2)有放回简单随机抽样求出抽到的2人为1名男生和1名女生的概率.
17.已知△ABC的三个顶点A(3,7),B(–2,5),C(–3,–5),点D为AC的中点.
(1)求点D的坐标;
(2)求直线BD的方程.
(3)求△ABD的面积.
18.如图,在四棱锥中,底面是正方形,侧棱底面,.
(1)求直线与直线所成角;
(2)求平面与平面的夹角.
19.2020年是我国网络建设的加速之年.截至2020年底,中国已建成全球最大的网络.为了切实推动移动网络质量提升,不断改善用户体验,中国信通院受工信部委托,定期在全国范围内开展重点场所移动网络质量专项测评.其中一项测评内容是在每座受测城市中挑选一条典型路段,以评估当地网络发展水平.其中5座受测城市的综合下载速率(单位:)数据如下表:
城市 路段 综合下载速率(单位:)
福州 五四路 708.92
广州 大学城外/中/内环 817.13
哈尔滨 红军街 630.34
杭州 环城东路 882.60
成都 二环高架 916.02
(1)从以上5座城市中随机选取2座城市进行分析,求选取的2座城市“综合下载速率”都大于800的概率;
(2)甲 乙两家网络运营商分别从以上5座城市中随机选取1座城市考察(甲 乙的选取互不影响),求甲 乙两家运营商中恰有1家选取的城市“综合下载速率”大于800的概率.
20.如图,四棱锥中,是以为斜边的等腰直角三角形,,,为的中点.
(1)求直线与平面所成角的正弦值;
(2)设是线段上一点,如果点是在平面内,判断点在线段的位置并证明你的结论;
(3)点在线段上运动,求点到直线的距离最大值.
21.我们知道,在平面中,给定一点和一条直线的法向量可以唯一确定一条直线. 如点在直线上,为直线的一个法向量,则直线上任意一点满足,则,化简可得,即为直线的方程. 类似的,在空间中,给定一点和一个平面的法向量可以唯一确定一个平面.
(1)若在空间直角坐标系中,,请利用平面的法向量求出平面的方程;
(2)试写出平面(不同时为0)的一个法向量(无需证明),并求出点到平面的距离.
试卷第1页,共3页
试卷第1页,共3页
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B D D C D B A C
11.8
12.0.74
13.
14.
15.
16.(1)从5名学生中,不放回地任意依次抽取2名学生的所有可能结果为:
,
共20种结果.
设事件为抽到的2人为1名男生和1名女生,则事件发生的所有可能结果为:
,共12种结果.
由古典概型的概率计算公式得:,
即不放回简单随机抽样求出抽到的2人为1名男生和1名女生的概率为.
(2)有放回简单随机抽样抽取2名学生的所有可能结果为:
,共25种结果.
设事件为抽到的2人为1名男生和1名女生,则事件发生的所有可能结果为:
,共12种结果.
由古典概型的概率计算公式得:,
即有放回简单随机抽样求出抽到的2人为1名男生和1名女生的概率为.
17.(1)设D(x,y),
则,,
∴点D的坐标为(0,1).
(2)∵直线BD的斜率为.
∴直线BD的方程为:y–1=–2(x–0),即2x+y–1=0.
(3)∵,
∴A到直线BD的距离为.
∴△ABD的面积为.
18.(1)底面,平面,,
则直线与直线所成的角为.
(2)由题意,底面是正方形,侧棱底面,
则以点为坐标原点,建立如图所示空间直角坐标系,
则,,,,
所以,,,
设平面的一个法向量为,
则,令则,
设平面的一个法向量为,
则,令,则,
则,
又平面与平面的夹角为锐角,
所以平面与平面的夹角为.
19.解:(1)5座城市中“综合下载速率”大于800Mbps的有3座,设为,
“综合下载速率”不大于800的有2座,设为.
随机选取2座城市所有可能为:,,,,,,,,,共10种.
其中2座城市“综合下载速率”都大于800的有,,共3种.
设两个城市“综合下载速率”都大于800为事件,
所以
(2)设甲选取的城市“综合下载速率”大于800为事件,乙选取的城市“综合下载速率”大于800为事件,恰有1家运营商选取的城市“综合下载速率”大于800为事件.
依题意,事件,
所以
.
20.(1)直角梯形中,由已知可得,,
∴,即,
又是以为斜边的等腰直角三角形,∴,
取中点,连接,则,,
则,∴,
又,∴,
∴,,而,平面,
∴平面,
因此可以为轴,过平行于的直线为轴建立空间直角坐标系,如图,
则,,,,,
,,
设平面的一个法向量为,
则,取,则,即,
又,
,
直线PB与平面PAC所成角为,则.
(2)是的中点,证明如下:
,,,,为的中点,
所以,设,
则,
若点是在平面内,则,
则,解得,所以是的中点.
(3)设,,,,
,,
所以点到直线的距离为
,所以点到直线的距离最大值为.
21.(1)在平面中,,
设平面的法向量为,
所以,即,令,则,
所以.
设平面内任意一点,则.
所以,化简得.
所以平面的方程为.
(2)平面的法向量可取.
证明如下:
设为平面的任意两个点,
则,,
两式相减得,
即,即,
所以平面的法向量可取.
因为A,B,C不同时为0,所以不妨令,
平面上可取点,
所以,
则点H到平面的距离.
答案第1页,共2页
答案第1页,共2页
同课章节目录
