17.4 一元二次方程的根与系数的关系 课件(共18张PPT)
文档属性
| 名称 | 17.4 一元二次方程的根与系数的关系 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-22 10:19:33 | ||
图片预览



文档简介
(共18张PPT)
*17.4 一元二次方程的根与系数的关系
复习回顾
1、一元二次方程的概念?
2、一元二次方程的解法有哪些?
3、解一元二次方程的注意事项?
1.一元二次方程的一般形式是什么?
3.一元二次方程的根的情况怎样确定?
2.一元二次方程的求根公式是什么?
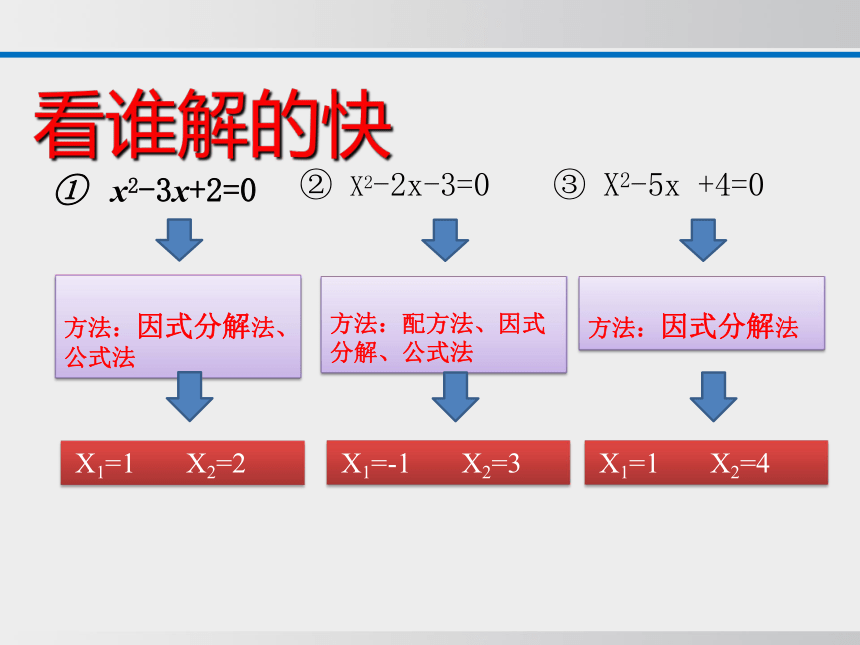
看谁解的快
① x2-3x+2=0
② X2-2x-3=0
③ X2-5x +4=0
方法:因式分解法、公式法
X1=1 X2=2
方法:配方法、因式分解、公式法
X1=-1 X2=3
方法:因式分解法
X1=1 X2=4
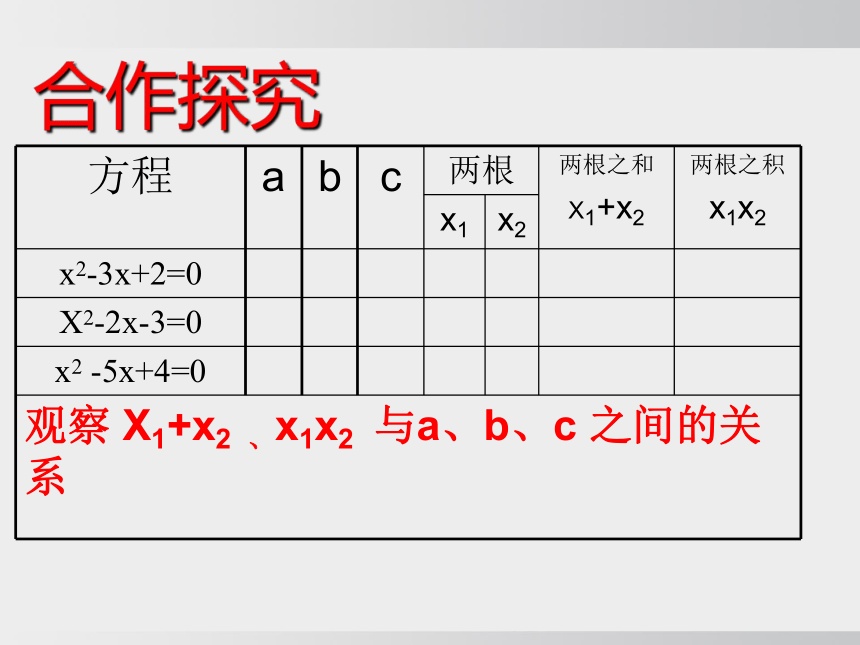
方程 a b c 两根 两根之和
X1+x2 两根之积
x1x2
x1 x2
x2-3x+2=0
X2-2x-3=0
x2 -5x+4=0
观察 X1+x2 、x1x2 与a、b、c 之间的关系
合作探究
方程 a b c 两根 两根之和
X1+x2 两根之积
x1x2
x1 x2
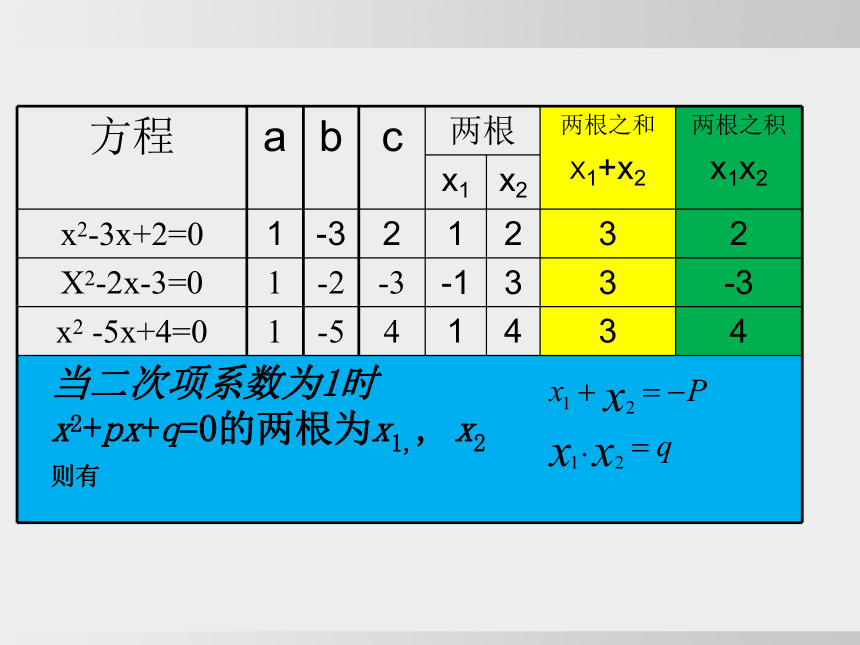
x2-3x+2=0 1 -3 2 1 2 3 2
X2-2x-3=0 1 -2 -3 -1 3 3 -3
x2 -5x+4=0 1 -5 4 1 4 3 4
当二次项系数为1时
x2+px+q=0的两根为x1,, x2
则有
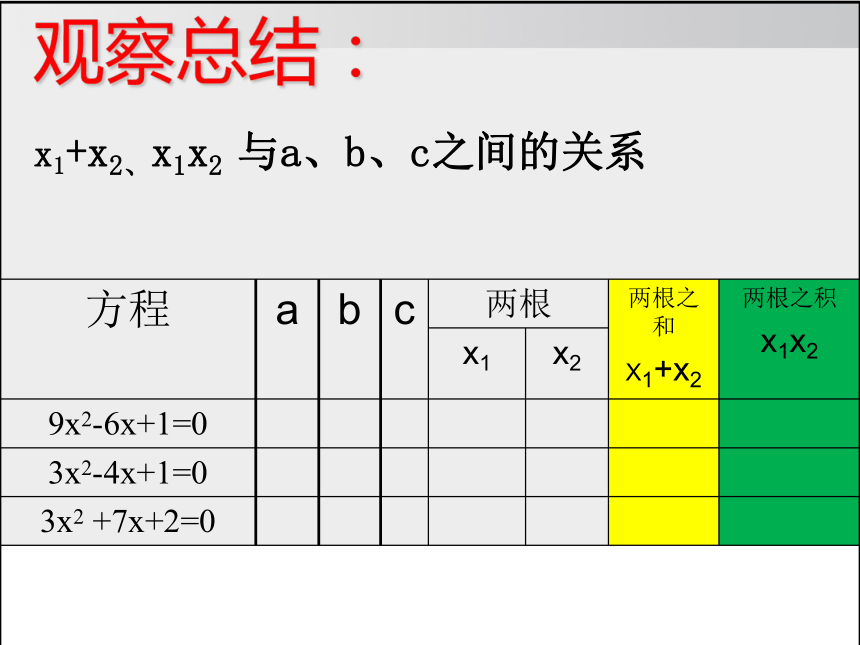
观察总结:
x1+x2、x1x2 与a、b、c之间的关系
方程 a b c 两根 两根之和
X1+x2 两根之积
x1x2
x1 x2
9x2-6x+1=0
3x2-4x+1=0
3x2 +7x+2=0
方程 a b c 两根 两根之和
X1+x2 两根之积
x1x2
x1 x2
9x2-6x+1=0 9 -6 1 1/3 1/3 2/3 1/9
3x2-4x+1=0 3 -4 1 1/3 1 4/3 1/3
3x2 +7x+2=0 3 7 2 -1/3 -2 -7/3 2/3
观察总结:x1+x2、x1x2 与a、b、c之间关系
猜想
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a=0 )的两根为x1、x2, 则 x1.x2 与系数a,b,c 的关系。
验证
一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是x1,x2
那么x1+x2= , x1x2=
注:能用公式的前提条件为b2-4ac≥0
这个关系通常称为韦达定理.
总 结
说出下列各方程的两根之和与两根之积:
1、 x2 - 2x - 1=0
2、 2x2 - 3x + =0
3、 2x2 - 6x =0
4、 3x2 = 4
x1+x2=2
x1x2=-1
x1+x2=3/2
x1+x2=3
x1+x2=0
x1x2=1/4
x1x2=0
x1x2= -4/3
说一说
例1 已知方程2x2 +kx-4=0的一个根是-4 ,求它的另一个根及k的值.
解:
设方程的另一个根为x2 ,则
解这方程组,得
答:方程的另一个根是 , k的值是7.
例2 方程2x2 -3x+1=0的 两个根记作x1 ,x2不解方程,求的值x1 – x2
解:
由韦达定理,得
1、已知方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值.
2、Rt△ABC 中,∠C=90°,a、b、c分别是 ∠A、 ∠B、 ∠C的对边,a、b是关于x的方程x2-7x+c+7=0 的两根,求AB边上的中线长.
课堂练习:
已知关于x的方程mx2-(2m-1)x+m-2=0(m﹥0)
(1)此方程有实数根吗?
(2)如果这个方程的两个实数根分别为x1 , x2 ,且 (x1-3)(x2-3)=5m,求m的值.
拓展练习:
1、熟练掌握根与系数的关系;
2、灵活运用根与系数关系解决问题;
3、探索解题思路,归纳解题思想方法.
小 结:
布置作业;
课堂作业:P39练习;
家庭作业 : (1)P40习题第2、3题;
(2)预习下一节内容.
*17.4 一元二次方程的根与系数的关系
复习回顾
1、一元二次方程的概念?
2、一元二次方程的解法有哪些?
3、解一元二次方程的注意事项?
1.一元二次方程的一般形式是什么?
3.一元二次方程的根的情况怎样确定?
2.一元二次方程的求根公式是什么?
看谁解的快
① x2-3x+2=0
② X2-2x-3=0
③ X2-5x +4=0
方法:因式分解法、公式法
X1=1 X2=2
方法:配方法、因式分解、公式法
X1=-1 X2=3
方法:因式分解法
X1=1 X2=4
方程 a b c 两根 两根之和
X1+x2 两根之积
x1x2
x1 x2
x2-3x+2=0
X2-2x-3=0
x2 -5x+4=0
观察 X1+x2 、x1x2 与a、b、c 之间的关系
合作探究
方程 a b c 两根 两根之和
X1+x2 两根之积
x1x2
x1 x2
x2-3x+2=0 1 -3 2 1 2 3 2
X2-2x-3=0 1 -2 -3 -1 3 3 -3
x2 -5x+4=0 1 -5 4 1 4 3 4
当二次项系数为1时
x2+px+q=0的两根为x1,, x2
则有
观察总结:
x1+x2、x1x2 与a、b、c之间的关系
方程 a b c 两根 两根之和
X1+x2 两根之积
x1x2
x1 x2
9x2-6x+1=0
3x2-4x+1=0
3x2 +7x+2=0
方程 a b c 两根 两根之和
X1+x2 两根之积
x1x2
x1 x2
9x2-6x+1=0 9 -6 1 1/3 1/3 2/3 1/9
3x2-4x+1=0 3 -4 1 1/3 1 4/3 1/3
3x2 +7x+2=0 3 7 2 -1/3 -2 -7/3 2/3
观察总结:x1+x2、x1x2 与a、b、c之间关系
猜想
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a=0 )的两根为x1、x2, 则 x1.x2 与系数a,b,c 的关系。
验证
一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是x1,x2
那么x1+x2= , x1x2=
注:能用公式的前提条件为b2-4ac≥0
这个关系通常称为韦达定理.
总 结
说出下列各方程的两根之和与两根之积:
1、 x2 - 2x - 1=0
2、 2x2 - 3x + =0
3、 2x2 - 6x =0
4、 3x2 = 4
x1+x2=2
x1x2=-1
x1+x2=3/2
x1+x2=3
x1+x2=0
x1x2=1/4
x1x2=0
x1x2= -4/3
说一说
例1 已知方程2x2 +kx-4=0的一个根是-4 ,求它的另一个根及k的值.
解:
设方程的另一个根为x2 ,则
解这方程组,得
答:方程的另一个根是 , k的值是7.
例2 方程2x2 -3x+1=0的 两个根记作x1 ,x2不解方程,求的值x1 – x2
解:
由韦达定理,得
1、已知方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值.
2、Rt△ABC 中,∠C=90°,a、b、c分别是 ∠A、 ∠B、 ∠C的对边,a、b是关于x的方程x2-7x+c+7=0 的两根,求AB边上的中线长.
课堂练习:
已知关于x的方程mx2-(2m-1)x+m-2=0(m﹥0)
(1)此方程有实数根吗?
(2)如果这个方程的两个实数根分别为x1 , x2 ,且 (x1-3)(x2-3)=5m,求m的值.
拓展练习:
1、熟练掌握根与系数的关系;
2、灵活运用根与系数关系解决问题;
3、探索解题思路,归纳解题思想方法.
小 结:
布置作业;
课堂作业:P39练习;
家庭作业 : (1)P40习题第2、3题;
(2)预习下一节内容.
