2024-2025学年人教版八年级数学上册第三次 (第11—15章 )阶段性综合练习题(含答案)
文档属性
| 名称 | 2024-2025学年人教版八年级数学上册第三次 (第11—15章 )阶段性综合练习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 516.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-22 00:00:00 | ||
图片预览

文档简介
2024-2025学年人教版八年级数学上册第三次 (第11—15章 )阶段性综合练习题
一、单选题(共10题;共30分)
1.(3分)有些地板的拼合图案如图所示,它是用正方形的地砖铺成的.用地砖铺地,用瓷砖贴墙,都要求砖与砖严丝合缝,不留空隙,把地面或墙面全部覆盖.从数学的角度看,这些工作就是用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)的问题.若商店出售下列形状地砖:①正方形;②长方形;③正五边形;④正六边形.若只选购其中某种地砖镶嵌地面,可供选择的地砖共有( )
A.1种 B.2种 C.3种 D.4种
2.(3分)如图,在中,交于点;在的延长线上取点,连接,已知,则为( )
A. B. C. D.
3.(3分)如图,的三边、、的长分别是8,10,14,其三条角平分线交于点O,将分为三个三角形,则等于( )
A. B. C. D.
4.(3分)当为正整数时,代数式一定是下面哪个数的倍数( )
A.3 B.5 C.7 D.8
5.(3分)如图,点A,B,C在同一直线上,在这条直线同侧作等边和等边,连接和,交点为M,交于点P,交于点Q,连接、,有4个结论:①,②,③,④,正确结论有( )
A.4 B.3 C.2 D.1
6.(3分)下面四个多项式中,能进行因式分解的是( )
A.x2+y2 B.x2﹣y C.x2﹣1 D.x2+x+1
7.(3分)如图,在中,,,射线是的角平分线,交于点D,过点B作的垂线与射线交于点E,连接,M是的中点,连接并延长与的延长线交于点G.则下列结论中:①;②垂直平分;③;④;⑤.正确的有( )
A.①②⑤ B.①③④ C.②③⑤ D.②③④
8.(3分)下列说法中:①若,,则;②两条直线被第三条直线所截,一组内错角的角平分线互相平行;③若,则或;④已知二元一次方程组的解也是二元一次方程的解,则a的值是0.5;其中正确的是( )
A.①② B.②③ C.①④ D.③④
9.(3分)如图,在△ABC中,AB=AC,∠BAC=36°,以点C为圆心,以BC为半径作弧交AC于点D,再分别以B,D为圆心,以大于BD的长为半径作弧,两弧相交于点P,作射线CP交AB于点E,连接DE.以下结论不正确的是( )
A.∠BCE=36° B.BC=AE
C. D.
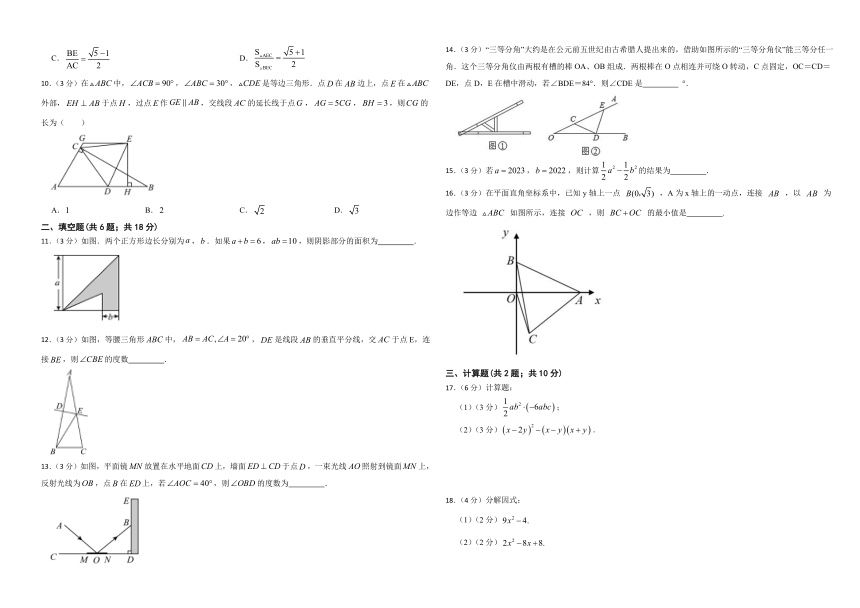
10.(3分)在中,,,是等边三角形.点在边上,点在外部,于点,过点作,交线段的延长线于点,,,则的长为( )
A. B. C. D.
二、填空题(共6题;共18分)
11.(3分)如图.两个正方形边长分别为,.如果,,则阴影部分的面积为 .
12.(3分)如图,等腰三角形中,,是线段的垂直平分线,交于点E,连接,则的度数 .
13.(3分)如图,平面镜放置在水平地面上,墙面于点,一束光线照射到镜面上,反射光线为,点在上,若,则的度数为 .
14.(3分)“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA、OB组成.两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°.则∠CDE是 °.
15.(3分)若,,则计算的结果为 .
16.(3分)在平面直角坐标系中,已知y轴上一点 ,A为x轴上的一动点,连接 ,以 为边作等边 如图所示,连接 ,则 的最小值是 .
三、计算题(共2题;共10分)
17.(6分)计算题:
(1)(3分);
(2)(3分).
18.(4分)分解因式:
(1)(2分)
(2)(2分)
四、解答题(共6题;共42分)
19.(5分)已知一个多边形每一个内角都是,求这个多边形的边数.
20.(6分)如图,,求的度数.
21.(6分) 如图,,,,经过点D.
(1)(2分)求证:;
(2)(2分)和有何数量和位置关系?请说明理由;
(3)(2分)若,求四边形的面积.
22.(7分)如图所示,在△ABC中,AB=AC,AC边上的中线把三角形的周长分为24cm和30cm的两部分,求三角形各边的长.
23.(8分)如图,在平面直角坐标系中,点A在x轴的负半轴上,其坐标为,点C在y轴的正半轴上,其坐标为,分别过点A、C作y轴、x轴的平行线,两平行线相交于B.
(1)(2分)点B坐标为(____,____);
(2)(3分)动点P从点B出发,以每秒2个单位长度的速沿向终点A匀速移动,设点P移动的时间为t秒,M为中点,N为中点,用含t的式子表示的长;
(3)(3分)在(2)的条件下,点P到达A后,继续沿着向终点O运动,连接,求t为何值时,把长方形分成的两部分面积比为,并求出此时点P坐标.
24.(10分)在中,.点D、E分别在的边上,且均不与的顶点重合,连接,将沿折叠,使点A的对称点始终落在四边形的外部,交边于点F,且点与点C在直线的异侧.
(1)(2分)如图①,则_______.
(2)(2分)如图②,则_______.
(3)(3分)如图③,设图②中的.求的度数;
(4)(3分)当的某条边与或垂直时,直接写出的度数.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】C
4.【答案】D
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】C
10.【答案】B
11.【答案】3
12.【答案】
13.【答案】
14.【答案】68
15.【答案】2022.5
16.【答案】3
17.【答案】(1)解:
;
(2)解:
.
18.【答案】(1)解:=;
(2)解:
19.【答案】9
20.【答案】
21.【答案】(1)解:∵,
∴,
∴.
在和中,
∴().
(2)解:,且,理由如下:
由(1)知且
在Rt中,,
∴,
即,
∴;
(3)解:∵,
∴,
∴.
22.【答案】解:根据题意画出图形,如下图,
设等腰三角形的腰长AB=AC=2x,BC=y,
∵BD是腰上的中线,
∴AD=DC=x,
若AB+AD的长为24,则2x+x=24,解得x=8,
则x+y=30,即8+y=30,解得y=22,
则等腰三角形的腰长为16厘米,底边长为22厘米,能够成三角形;
若AB+AD的长为30,则2x+x=30,解得x=10,
则x+y=24,即10+y=24,解得y=14;
则腰长为20cm,底长为14cm,能够成三角形.
23.【答案】(1)
(2)
(3),
24.【答案】(1)48
(2)222
(3)
(4)或
一、单选题(共10题;共30分)
1.(3分)有些地板的拼合图案如图所示,它是用正方形的地砖铺成的.用地砖铺地,用瓷砖贴墙,都要求砖与砖严丝合缝,不留空隙,把地面或墙面全部覆盖.从数学的角度看,这些工作就是用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)的问题.若商店出售下列形状地砖:①正方形;②长方形;③正五边形;④正六边形.若只选购其中某种地砖镶嵌地面,可供选择的地砖共有( )
A.1种 B.2种 C.3种 D.4种
2.(3分)如图,在中,交于点;在的延长线上取点,连接,已知,则为( )
A. B. C. D.
3.(3分)如图,的三边、、的长分别是8,10,14,其三条角平分线交于点O,将分为三个三角形,则等于( )
A. B. C. D.
4.(3分)当为正整数时,代数式一定是下面哪个数的倍数( )
A.3 B.5 C.7 D.8
5.(3分)如图,点A,B,C在同一直线上,在这条直线同侧作等边和等边,连接和,交点为M,交于点P,交于点Q,连接、,有4个结论:①,②,③,④,正确结论有( )
A.4 B.3 C.2 D.1
6.(3分)下面四个多项式中,能进行因式分解的是( )
A.x2+y2 B.x2﹣y C.x2﹣1 D.x2+x+1
7.(3分)如图,在中,,,射线是的角平分线,交于点D,过点B作的垂线与射线交于点E,连接,M是的中点,连接并延长与的延长线交于点G.则下列结论中:①;②垂直平分;③;④;⑤.正确的有( )
A.①②⑤ B.①③④ C.②③⑤ D.②③④
8.(3分)下列说法中:①若,,则;②两条直线被第三条直线所截,一组内错角的角平分线互相平行;③若,则或;④已知二元一次方程组的解也是二元一次方程的解,则a的值是0.5;其中正确的是( )
A.①② B.②③ C.①④ D.③④
9.(3分)如图,在△ABC中,AB=AC,∠BAC=36°,以点C为圆心,以BC为半径作弧交AC于点D,再分别以B,D为圆心,以大于BD的长为半径作弧,两弧相交于点P,作射线CP交AB于点E,连接DE.以下结论不正确的是( )
A.∠BCE=36° B.BC=AE
C. D.
10.(3分)在中,,,是等边三角形.点在边上,点在外部,于点,过点作,交线段的延长线于点,,,则的长为( )
A. B. C. D.
二、填空题(共6题;共18分)
11.(3分)如图.两个正方形边长分别为,.如果,,则阴影部分的面积为 .
12.(3分)如图,等腰三角形中,,是线段的垂直平分线,交于点E,连接,则的度数 .
13.(3分)如图,平面镜放置在水平地面上,墙面于点,一束光线照射到镜面上,反射光线为,点在上,若,则的度数为 .
14.(3分)“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA、OB组成.两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°.则∠CDE是 °.
15.(3分)若,,则计算的结果为 .
16.(3分)在平面直角坐标系中,已知y轴上一点 ,A为x轴上的一动点,连接 ,以 为边作等边 如图所示,连接 ,则 的最小值是 .
三、计算题(共2题;共10分)
17.(6分)计算题:
(1)(3分);
(2)(3分).
18.(4分)分解因式:
(1)(2分)
(2)(2分)
四、解答题(共6题;共42分)
19.(5分)已知一个多边形每一个内角都是,求这个多边形的边数.
20.(6分)如图,,求的度数.
21.(6分) 如图,,,,经过点D.
(1)(2分)求证:;
(2)(2分)和有何数量和位置关系?请说明理由;
(3)(2分)若,求四边形的面积.
22.(7分)如图所示,在△ABC中,AB=AC,AC边上的中线把三角形的周长分为24cm和30cm的两部分,求三角形各边的长.
23.(8分)如图,在平面直角坐标系中,点A在x轴的负半轴上,其坐标为,点C在y轴的正半轴上,其坐标为,分别过点A、C作y轴、x轴的平行线,两平行线相交于B.
(1)(2分)点B坐标为(____,____);
(2)(3分)动点P从点B出发,以每秒2个单位长度的速沿向终点A匀速移动,设点P移动的时间为t秒,M为中点,N为中点,用含t的式子表示的长;
(3)(3分)在(2)的条件下,点P到达A后,继续沿着向终点O运动,连接,求t为何值时,把长方形分成的两部分面积比为,并求出此时点P坐标.
24.(10分)在中,.点D、E分别在的边上,且均不与的顶点重合,连接,将沿折叠,使点A的对称点始终落在四边形的外部,交边于点F,且点与点C在直线的异侧.
(1)(2分)如图①,则_______.
(2)(2分)如图②,则_______.
(3)(3分)如图③,设图②中的.求的度数;
(4)(3分)当的某条边与或垂直时,直接写出的度数.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】C
4.【答案】D
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】C
10.【答案】B
11.【答案】3
12.【答案】
13.【答案】
14.【答案】68
15.【答案】2022.5
16.【答案】3
17.【答案】(1)解:
;
(2)解:
.
18.【答案】(1)解:=;
(2)解:
19.【答案】9
20.【答案】
21.【答案】(1)解:∵,
∴,
∴.
在和中,
∴().
(2)解:,且,理由如下:
由(1)知且
在Rt中,,
∴,
即,
∴;
(3)解:∵,
∴,
∴.
22.【答案】解:根据题意画出图形,如下图,
设等腰三角形的腰长AB=AC=2x,BC=y,
∵BD是腰上的中线,
∴AD=DC=x,
若AB+AD的长为24,则2x+x=24,解得x=8,
则x+y=30,即8+y=30,解得y=22,
则等腰三角形的腰长为16厘米,底边长为22厘米,能够成三角形;
若AB+AD的长为30,则2x+x=30,解得x=10,
则x+y=24,即10+y=24,解得y=14;
则腰长为20cm,底长为14cm,能够成三角形.
23.【答案】(1)
(2)
(3),
24.【答案】(1)48
(2)222
(3)
(4)或
同课章节目录
