选择必修第二册 第四章 4.3.1 等比数列的概念(第2课时 ) 课件(共31张PPT)
文档属性
| 名称 | 选择必修第二册 第四章 4.3.1 等比数列的概念(第2课时 ) 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-21 17:11:16 | ||
图片预览











文档简介
(共31张PPT)
选择必修2
第四章 数列
4.3 等比数列
4.3.1 等比数列的概念(第2课时)
教学目标
学习目标 数学素养
1.掌握等比数列的相关性质,并能灵活运用. 1.数学抽象素养和逻辑推理素养.
2.会运用等比数列解决一些实际问题. 2.数学抽象素养和化归与转化素养.
温故知新
等比数列
定义
符号表示
公比
通项公式
等比中项
通项公式推导方法
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列
(n≥2,).
().
an=a1qn-1.
.
公比q可正、可负但不可为零
G是a与b的等比中项 G2=ab(ab>0).
不完全归纳法
累乘法
温故知新
当q=1时,等比数列{an}是非零常数数列,不具备单调性.
新知探究
【例1】用10000元购买某个理财产品一年.
⑴若以月利率0.4%的复利利息,12个月能获得多少利息(精确到1元)?
⑵若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于⑴中按月结算的利息(精确到10-5)?
分析:复利是指把前一期的利息与本金之和算作本金,再计算下一期的利息.所以
存入本金 : a元,
第1期末本利和: a+ar=a(1+r),
第2期末本利和:a(1+r)+a(1+r)r=a(1+r)2 元,
第3期末本利和:a(1+r)2+a(1+r)2r=a(1+r)3 元,
……
每一期的本金与利息的和构成等比数列.
这个等比数列的首项是a(1+r),公比是(1+r).
可得通项公式为an=a(1+r)(1+r)n -1=a(1+r)n .
新知探究
【例1】用10000元购买某个理财产品一年.
⑴若以月利率0.4%的复利利息,12个月能获得多少利息(精确到1元)?
⑵若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于⑴中按月结算的利息(精确到10-5)?
分析:⑴ 实际问题
数学问题
设本利和组成数列
“用 10000元购买某个理财产品”
本金10000
“月利率”
12个月能获得的本利和
的值
“12个月能获得的利息”
利息=本利和-本金
=
新知探究
【例1】用10000元购买某个理财产品一年.
⑴若以月利率0.4%的复利利息,12个月能获得多少利息(精确到1元)?
⑵若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于⑴中按月结算的利息(精确到10-5)?
解:
⑴设这笔钱存n个月以后的本金利息和组成一个数列{an },
则{an }是等比数列,
首项a1=104(1+0.4%),公比q=1+0.4%,
所以a12=a1q11=104(1+0.4%)12≈10490.702.
所以,12个月后的利息为10490.702-104≈490.7(元).
新知探究
【例1】用10000元购买某个理财产品一年.
⑴若以月利率0.4%的复利利息,12个月能获得多少利息(精确到1元)?
⑵若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于⑴中按月结算的利息(精确到10-5)?
分析:⑵ 实际问题
数学问题
设本利和组成数列
“季度利息”
设为r,公比是(1+r)
存4个季度的本利和
b4
“存4个季度结算的利息”
b4 -a
“按季结算的利息不少于按月结算的利息”
b4 -a ≥a12-a
新知探究
【例1】用10000元购买某个理财产品一年.
⑴若以月利率0.4%的复利利息,12个月能获得多少利息(精确到1元)?
⑵若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于⑴中按月结算的利息(精确到10-5)?
解:
⑵设季度利率为r,这笔钱存n个季度以后的本金利息和组成一个数列{bn },
则{bn }也是等比数列,
首项b1=104(1+r),,公比1+r,
于是b4=104(1+r)4 .
所以,当季度利率不小于1.205%时,按季结算得利息不少于按月结算得利息.
因此,以季度复利计息,存4个季度后的利息为
[104(1+r)4 -104]元.
解不等式104(1+r)4 -104 ≥490.7,得
r≥1.205%.
新知探究
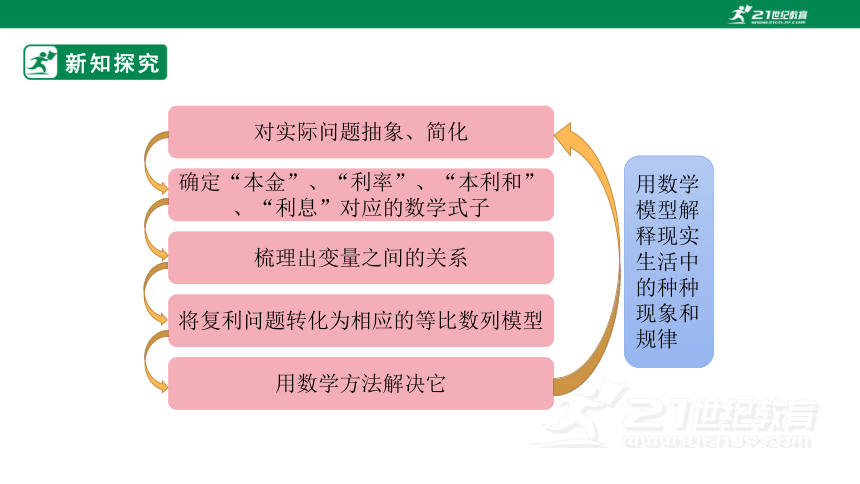
对实际问题抽象、简化
梳理出变量之间的关系
将复利问题转化为相应的等比数列模型
用数学模型解释现实生活中的种种现象和规律
用数学方法解决它
确定“本金”、“利率”、“本利和”、“利息”对应的数学式子
初试身手
设从2024年1月开始,第n个月该厂的生产总值是an万元,则
1.某工厂2024年1月的生产总值为a万元,计划从2024年2月起,每月生产总值比上一个月增长m%,那么到2025年8月底该厂的生产总值为多少万元?
∴2025年8月底该厂的生产总值为a20=a(1+m%)20-1=a(1+m%)19(万元).
解:
an+1=an+anm%=(1+m%)an,
∴数列{an}是首项a1=a,公比q=1+m%的等比数列.
∴1+m%.
∴an=a(1+m%)n-1.
知新探究
【例2】已知数列{an}的首项a1=3.
⑴若{an }为等差数列,公差d=2 ,证明数列{}为等比数列;
⑵若 {an }为等比数列 ,公 比q=,证明数列{log3an }为等差数列.
分析:证明等比数列有如下方法:
①定义法:为等比数列.
②等比中项法:为等比数列.
③通项公式法:为等比数列.
根据题意,本题需要从等差数列、等比数列的定义出发,利用指数、对数的知识证明.
知新探究
【例2】已知数列{an}的首项a1=3.
⑴若{an }为等差数列,公差d=2 ,证明数列{}为等比数列;
⑵若 {an }为等比数列 ,公 比q=,证明数列{log3an }为等差数列.
解:
⑴由a1=3 ,d=2 ,{an }的通项公式为an=2n+1.
9,
又b1=33=27,
设bn==32n+1,则
所以数列{}是以27为首项, 9为公比的等比数列.
知新探究
【例2】已知数列{an}的首项a1=3.
⑴若{an }为等差数列,公差d=2 ,证明数列{}为等比数列;
⑵若 {an }为等比数列 ,公 比q=,证明数列{log3an }为等差数列.
解:
⑵由a1=3 ,q= ,得
,
所以log3an-log3an=[3-2(n+1)]-(3-2n)=-2.
an=.
两边同时取以3为底的对数,得
所以数列{log3an }是首项为1, 公比为-2的等差数列.
又log3a1=log33=1,
知新探究
已知如果数列为等差数列,那么数列是否一定为等比数列?如果数列是各项均为正数的等比数列,那么数列是否一定为等差数列?
解:
数列一定为等比数列.
证明:设等差数列{an }首项为a1 ,公差为d,则
.
所以, 是以为首项, 为公比的等比数列.
数列是等差数列
数列是等比数列
知新探究
已知如果数列为等差数列,那么数列是否一定为等比数列?如果数列是各项均为正数的等比数列,那么数列是否一定为等差数列?
解:
数列一定为等差数列.
证明:设等比数列{an }首项为a1 ,公比为q,则
.
所以, 是首项为, 公差为的等差数列.
数列是各项均为正
的等比数列
数列是等差数列
初试身手
⑴证明:由a1=2,an+1=4an-3n+1,得
2.已知a1=2,an+1=4an-3n+1.
⑴证明:数列{an-n}是等比数列;
⑵求数列{an}的通项公式.
an-n=1×4n-1=4n-1.
解:
⑵由⑴可得
∴,
a1-1=1,an+1-(n+1)=4(an-n),
∴数列{an-n}是首项为1,公比为4的等比数列.
∴an=4n-1+n.
知新探究
【例3】某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加
0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
解:
设从今年1月起,各月的产量及不合格率分别构成数列{an}、{bn},由题意,知
an=1050×1.05n-1,
bn=1-[90%+0.4%(n-1)]=0.104-0.004n.其中n=1,2,…,24,
分析:设从今年1月起,各月的产量及不合格率分别构成数列{an}、{bn},则各月不合格品的数量构成数列{anbn}.由题意得,数列{an}是等比数列,{bn}是等差数列.由于数列{anbn}既非等差数列又非等比数列,所以可以先列表观察规律,再寻找问题的解决方法.
anbn=1050×1.05n-1×(0.104-0.004n)=1.05n×(104-4n)
知新探究
【例3】某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加
0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
解:
由计算工具计算(精确到0.10),并列表(如下表).
观察发现,数列{anbn}先递增,在第6项以后递减,所以只要设法证明当n≥6时,
{anbn}递减,且a13b13<100即可.
anbn=1050×1.05n-1×(0.104-0.004n)=1.05n×(104-4n)
知新探究
【例3】某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加
0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
解:
得n>5.
观察发现,数列{anbn}先递增,在第6项以后递减,所以只要设法证明当n≥6时,
{anbn}递减,且a13b13<100即可.
所以,当n≥6时,{anbn}递减.
由.
又a13b13≈98<100,
所以,当13≤n≤24时,anbn≤a13b13<100.
所以,生产该产品一年后,月不合格品的数量能否控制在100个以内.
初试身手
设该养猪场从2021年起每年年初猪的存栏数依次为a1,a2,a3,…,由题意可得
3.某养猪场2021年年初猪的存栏数为1500,预计以后每年存栏数的增长率为8%,且在每年年底卖出100头,则2036年年初猪的存栏数约为(参考数据:1.0814≈2.9,1.0815≈3.2,1.0816≈3.4) ( )
A.2050 B.2150 C.2250 D.2350
2036年年初即n=16,
解:
∴an-1250=250·1.08n-1.
即an+1-1250=1.08(an-1250),
an+1=an×(1+8%)-100,
∴数列{an-1250}是首项为a1-1250=250,公比为1.08的等比数列.
∴a16=250×1.0815+1250≈2050.故选A.
知新探究
等比数列的性质
⑴若数列{an},{bn}是项数相同的等比数列,则{an·bn}也是等比数列.特别地,若{an}是等比数列,c是不等于0的常数,则{c·an}也是等比数列.
⑵在等比数列{an}中,若m+n=p+q,则aman=apaq.
⑶若等比数列{an}是有穷数列,则与首末两项等距离的两项的积相等,且等于首末两项的积.
⑷在等比数列{an}中,每隔k项取出一项,按原来的顺序排列,所得新数列仍为等比数列,公比为qk+1.
⑸在等比数列{an}中,当m,n,p(m,n,p∈N*)成等差数列时,am,an,ap成等比数列.
在应用等比数列的性质解题时,需时刻注意等比数列性质成立的前提条件.
知新探究
【例4】⑴已知各项均为正数的等比数列{an}中,a1a2a3=5,a7a8a9=10,则a4a5a6=( )
A.5 B.7 C.6 D.±5
⑵已知等比数列{an}满足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n-1=( )
A.n(2n-1) B.(n+1)2 C.n2 D.(n-1)2
解:
所以.
⑴方法1:由等比中项的性质知a1a2a3==5,a7a8a9==10,
所以,a4a5a6=.
所以,(a4a5a6)2=(a1a2a3)·(a7a8a9)=50,
方法2:由等比数列的性质知,a1a2a3,a4a5a6,a7a8a9构成等比数列,
又数列各项均为正数,所以a4a5a6=.
故选A.
故选A.
知新探究
【例4】⑴已知各项均为正数的等比数列{an}中,a1a2a3=5,a7a8a9=10,则a4a5a6=( )
A.5 B.7 C.6 D.±5
⑵已知等比数列{an}满足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n-1=( )
A.n(2n-1) B.(n+1)2 C.n2 D.(n-1)2
解:
即.
⑵方法1:由a5·a2n-5=22n,得
又an>0,所以an==2n.
则log2a1+log2a3+…+log2a2n-1=1+3+…+(2n-1)=n2.
知新探究
【例4】⑴已知各项均为正数的等比数列{an}中,a1a2a3=5,a7a8a9=10,则a4a5a6=( )
A.5 B.7 C.6 D.±5
⑵已知等比数列{an}满足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n-1=( )
A.n(2n-1) B.(n+1)2 C.n2 D.(n-1)2
解:
取特殊值,如令n=2,则log2a1+log2a3=log2(2·23)=log224=4.只有C选项符合.
⑵方法2:由等比中项的性质,得a5·a2n-5=(an)2=22n,注意到an>0,所以an=2n.
方法3:由等比中项的性质,得a5·a2n-5=(an)2=22n,注意到an>0,所以an=2n.
于是log2a1+log2a3+…+log2a2n-1=1+3+…+(2n-1)=n2.
初试身手
⑴由a2a15=a7a10,得
3.在等比数列{an}中.
⑴a2=3,a7a10=36,则a15等于( )
A.12 B.6 C.-12 D.-6
⑵若a7+a8+a9+a10=,a8a9=-,则=________.
=12.
解:
⑵∵,
∴.
由等比数列的性质,得a7a10=a8a9,
故选A.
课堂小结
1.等比数列的证明.
2.等比数列的有关计算问题.
3.等比数列的性质.
4.等比数列的应用问题.
作业布置
作业: P34 练习 第2,3,4,5题
补充:
已知{an}是等差数列,{bn}是公比为2的等比数列,且a2-b2=a3-b3=b4-a4.
⑴证明:a1=b1;
⑵求集合{k|bk=am+a1,1≤m≤500}中元素的个数.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修2
第四章 数列
4.3 等比数列
4.3.1 等比数列的概念(第2课时)
教学目标
学习目标 数学素养
1.掌握等比数列的相关性质,并能灵活运用. 1.数学抽象素养和逻辑推理素养.
2.会运用等比数列解决一些实际问题. 2.数学抽象素养和化归与转化素养.
温故知新
等比数列
定义
符号表示
公比
通项公式
等比中项
通项公式推导方法
一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列
(n≥2,).
().
an=a1qn-1.
.
公比q可正、可负但不可为零
G是a与b的等比中项 G2=ab(ab>0).
不完全归纳法
累乘法
温故知新
当q=1时,等比数列{an}是非零常数数列,不具备单调性.
新知探究
【例1】用10000元购买某个理财产品一年.
⑴若以月利率0.4%的复利利息,12个月能获得多少利息(精确到1元)?
⑵若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于⑴中按月结算的利息(精确到10-5)?
分析:复利是指把前一期的利息与本金之和算作本金,再计算下一期的利息.所以
存入本金 : a元,
第1期末本利和: a+ar=a(1+r),
第2期末本利和:a(1+r)+a(1+r)r=a(1+r)2 元,
第3期末本利和:a(1+r)2+a(1+r)2r=a(1+r)3 元,
……
每一期的本金与利息的和构成等比数列.
这个等比数列的首项是a(1+r),公比是(1+r).
可得通项公式为an=a(1+r)(1+r)n -1=a(1+r)n .
新知探究
【例1】用10000元购买某个理财产品一年.
⑴若以月利率0.4%的复利利息,12个月能获得多少利息(精确到1元)?
⑵若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于⑴中按月结算的利息(精确到10-5)?
分析:⑴ 实际问题
数学问题
设本利和组成数列
“用 10000元购买某个理财产品”
本金10000
“月利率”
12个月能获得的本利和
的值
“12个月能获得的利息”
利息=本利和-本金
=
新知探究
【例1】用10000元购买某个理财产品一年.
⑴若以月利率0.4%的复利利息,12个月能获得多少利息(精确到1元)?
⑵若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于⑴中按月结算的利息(精确到10-5)?
解:
⑴设这笔钱存n个月以后的本金利息和组成一个数列{an },
则{an }是等比数列,
首项a1=104(1+0.4%),公比q=1+0.4%,
所以a12=a1q11=104(1+0.4%)12≈10490.702.
所以,12个月后的利息为10490.702-104≈490.7(元).
新知探究
【例1】用10000元购买某个理财产品一年.
⑴若以月利率0.4%的复利利息,12个月能获得多少利息(精确到1元)?
⑵若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于⑴中按月结算的利息(精确到10-5)?
分析:⑵ 实际问题
数学问题
设本利和组成数列
“季度利息”
设为r,公比是(1+r)
存4个季度的本利和
b4
“存4个季度结算的利息”
b4 -a
“按季结算的利息不少于按月结算的利息”
b4 -a ≥a12-a
新知探究
【例1】用10000元购买某个理财产品一年.
⑴若以月利率0.4%的复利利息,12个月能获得多少利息(精确到1元)?
⑵若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于⑴中按月结算的利息(精确到10-5)?
解:
⑵设季度利率为r,这笔钱存n个季度以后的本金利息和组成一个数列{bn },
则{bn }也是等比数列,
首项b1=104(1+r),,公比1+r,
于是b4=104(1+r)4 .
所以,当季度利率不小于1.205%时,按季结算得利息不少于按月结算得利息.
因此,以季度复利计息,存4个季度后的利息为
[104(1+r)4 -104]元.
解不等式104(1+r)4 -104 ≥490.7,得
r≥1.205%.
新知探究
对实际问题抽象、简化
梳理出变量之间的关系
将复利问题转化为相应的等比数列模型
用数学模型解释现实生活中的种种现象和规律
用数学方法解决它
确定“本金”、“利率”、“本利和”、“利息”对应的数学式子
初试身手
设从2024年1月开始,第n个月该厂的生产总值是an万元,则
1.某工厂2024年1月的生产总值为a万元,计划从2024年2月起,每月生产总值比上一个月增长m%,那么到2025年8月底该厂的生产总值为多少万元?
∴2025年8月底该厂的生产总值为a20=a(1+m%)20-1=a(1+m%)19(万元).
解:
an+1=an+anm%=(1+m%)an,
∴数列{an}是首项a1=a,公比q=1+m%的等比数列.
∴1+m%.
∴an=a(1+m%)n-1.
知新探究
【例2】已知数列{an}的首项a1=3.
⑴若{an }为等差数列,公差d=2 ,证明数列{}为等比数列;
⑵若 {an }为等比数列 ,公 比q=,证明数列{log3an }为等差数列.
分析:证明等比数列有如下方法:
①定义法:为等比数列.
②等比中项法:为等比数列.
③通项公式法:为等比数列.
根据题意,本题需要从等差数列、等比数列的定义出发,利用指数、对数的知识证明.
知新探究
【例2】已知数列{an}的首项a1=3.
⑴若{an }为等差数列,公差d=2 ,证明数列{}为等比数列;
⑵若 {an }为等比数列 ,公 比q=,证明数列{log3an }为等差数列.
解:
⑴由a1=3 ,d=2 ,{an }的通项公式为an=2n+1.
9,
又b1=33=27,
设bn==32n+1,则
所以数列{}是以27为首项, 9为公比的等比数列.
知新探究
【例2】已知数列{an}的首项a1=3.
⑴若{an }为等差数列,公差d=2 ,证明数列{}为等比数列;
⑵若 {an }为等比数列 ,公 比q=,证明数列{log3an }为等差数列.
解:
⑵由a1=3 ,q= ,得
,
所以log3an-log3an=[3-2(n+1)]-(3-2n)=-2.
an=.
两边同时取以3为底的对数,得
所以数列{log3an }是首项为1, 公比为-2的等差数列.
又log3a1=log33=1,
知新探究
已知如果数列为等差数列,那么数列是否一定为等比数列?如果数列是各项均为正数的等比数列,那么数列是否一定为等差数列?
解:
数列一定为等比数列.
证明:设等差数列{an }首项为a1 ,公差为d,则
.
所以, 是以为首项, 为公比的等比数列.
数列是等差数列
数列是等比数列
知新探究
已知如果数列为等差数列,那么数列是否一定为等比数列?如果数列是各项均为正数的等比数列,那么数列是否一定为等差数列?
解:
数列一定为等差数列.
证明:设等比数列{an }首项为a1 ,公比为q,则
.
所以, 是首项为, 公差为的等差数列.
数列是各项均为正
的等比数列
数列是等差数列
初试身手
⑴证明:由a1=2,an+1=4an-3n+1,得
2.已知a1=2,an+1=4an-3n+1.
⑴证明:数列{an-n}是等比数列;
⑵求数列{an}的通项公式.
an-n=1×4n-1=4n-1.
解:
⑵由⑴可得
∴,
a1-1=1,an+1-(n+1)=4(an-n),
∴数列{an-n}是首项为1,公比为4的等比数列.
∴an=4n-1+n.
知新探究
【例3】某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加
0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
解:
设从今年1月起,各月的产量及不合格率分别构成数列{an}、{bn},由题意,知
an=1050×1.05n-1,
bn=1-[90%+0.4%(n-1)]=0.104-0.004n.其中n=1,2,…,24,
分析:设从今年1月起,各月的产量及不合格率分别构成数列{an}、{bn},则各月不合格品的数量构成数列{anbn}.由题意得,数列{an}是等比数列,{bn}是等差数列.由于数列{anbn}既非等差数列又非等比数列,所以可以先列表观察规律,再寻找问题的解决方法.
anbn=1050×1.05n-1×(0.104-0.004n)=1.05n×(104-4n)
知新探究
【例3】某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加
0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
解:
由计算工具计算(精确到0.10),并列表(如下表).
观察发现,数列{anbn}先递增,在第6项以后递减,所以只要设法证明当n≥6时,
{anbn}递减,且a13b13<100即可.
anbn=1050×1.05n-1×(0.104-0.004n)=1.05n×(104-4n)
知新探究
【例3】某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加
0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
解:
得n>5.
观察发现,数列{anbn}先递增,在第6项以后递减,所以只要设法证明当n≥6时,
{anbn}递减,且a13b13<100即可.
所以,当n≥6时,{anbn}递减.
由.
又a13b13≈98<100,
所以,当13≤n≤24时,anbn≤a13b13<100.
所以,生产该产品一年后,月不合格品的数量能否控制在100个以内.
初试身手
设该养猪场从2021年起每年年初猪的存栏数依次为a1,a2,a3,…,由题意可得
3.某养猪场2021年年初猪的存栏数为1500,预计以后每年存栏数的增长率为8%,且在每年年底卖出100头,则2036年年初猪的存栏数约为(参考数据:1.0814≈2.9,1.0815≈3.2,1.0816≈3.4) ( )
A.2050 B.2150 C.2250 D.2350
2036年年初即n=16,
解:
∴an-1250=250·1.08n-1.
即an+1-1250=1.08(an-1250),
an+1=an×(1+8%)-100,
∴数列{an-1250}是首项为a1-1250=250,公比为1.08的等比数列.
∴a16=250×1.0815+1250≈2050.故选A.
知新探究
等比数列的性质
⑴若数列{an},{bn}是项数相同的等比数列,则{an·bn}也是等比数列.特别地,若{an}是等比数列,c是不等于0的常数,则{c·an}也是等比数列.
⑵在等比数列{an}中,若m+n=p+q,则aman=apaq.
⑶若等比数列{an}是有穷数列,则与首末两项等距离的两项的积相等,且等于首末两项的积.
⑷在等比数列{an}中,每隔k项取出一项,按原来的顺序排列,所得新数列仍为等比数列,公比为qk+1.
⑸在等比数列{an}中,当m,n,p(m,n,p∈N*)成等差数列时,am,an,ap成等比数列.
在应用等比数列的性质解题时,需时刻注意等比数列性质成立的前提条件.
知新探究
【例4】⑴已知各项均为正数的等比数列{an}中,a1a2a3=5,a7a8a9=10,则a4a5a6=( )
A.5 B.7 C.6 D.±5
⑵已知等比数列{an}满足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n-1=( )
A.n(2n-1) B.(n+1)2 C.n2 D.(n-1)2
解:
所以.
⑴方法1:由等比中项的性质知a1a2a3==5,a7a8a9==10,
所以,a4a5a6=.
所以,(a4a5a6)2=(a1a2a3)·(a7a8a9)=50,
方法2:由等比数列的性质知,a1a2a3,a4a5a6,a7a8a9构成等比数列,
又数列各项均为正数,所以a4a5a6=.
故选A.
故选A.
知新探究
【例4】⑴已知各项均为正数的等比数列{an}中,a1a2a3=5,a7a8a9=10,则a4a5a6=( )
A.5 B.7 C.6 D.±5
⑵已知等比数列{an}满足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n-1=( )
A.n(2n-1) B.(n+1)2 C.n2 D.(n-1)2
解:
即.
⑵方法1:由a5·a2n-5=22n,得
又an>0,所以an==2n.
则log2a1+log2a3+…+log2a2n-1=1+3+…+(2n-1)=n2.
知新探究
【例4】⑴已知各项均为正数的等比数列{an}中,a1a2a3=5,a7a8a9=10,则a4a5a6=( )
A.5 B.7 C.6 D.±5
⑵已知等比数列{an}满足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n-1=( )
A.n(2n-1) B.(n+1)2 C.n2 D.(n-1)2
解:
取特殊值,如令n=2,则log2a1+log2a3=log2(2·23)=log224=4.只有C选项符合.
⑵方法2:由等比中项的性质,得a5·a2n-5=(an)2=22n,注意到an>0,所以an=2n.
方法3:由等比中项的性质,得a5·a2n-5=(an)2=22n,注意到an>0,所以an=2n.
于是log2a1+log2a3+…+log2a2n-1=1+3+…+(2n-1)=n2.
初试身手
⑴由a2a15=a7a10,得
3.在等比数列{an}中.
⑴a2=3,a7a10=36,则a15等于( )
A.12 B.6 C.-12 D.-6
⑵若a7+a8+a9+a10=,a8a9=-,则=________.
=12.
解:
⑵∵,
∴.
由等比数列的性质,得a7a10=a8a9,
故选A.
课堂小结
1.等比数列的证明.
2.等比数列的有关计算问题.
3.等比数列的性质.
4.等比数列的应用问题.
作业布置
作业: P34 练习 第2,3,4,5题
补充:
已知{an}是等差数列,{bn}是公比为2的等比数列,且a2-b2=a3-b3=b4-a4.
⑴证明:a1=b1;
⑵求集合{k|bk=am+a1,1≤m≤500}中元素的个数.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
