《 求阴影部分面积》教学设计
图片预览

文档简介
教学设计
课时教学设计
课题 求阴影部分的面积
课型 新授课□ 复习课 试卷讲评课□ 其它课□
教学内容分析 面积问题是中学数学的重要内容之一,每年全国各省市中考数学试题中,都有求阴影部分面积问题。阴影部分面积问题主要涉及扇形面积、特殊图形(直角三角形、菱形、矩形、等边三角形)的性质与面积计算,试题灵活多变,对学生的计算能力也有一定的要求。因此,重视和加强阴影部分面积的解法技巧的教学是十分必要的。本节课通过引导学生独立思考、动手实践、自主探索与合作交流,使学生理解和掌握基本的求解阴影部分面积所用到的数学知识与答题技巧、转化的数学思想和方法,获得基本的数学活动经验,从而增强发现和提出问题的能力、分析和解决问题的能力。
学情分析 九年级学生已经学习圆的相关知识,会计算扇形的面积,其他规则几何图形的面积计算也有基础,但是一般来说要求的阴影部分图形是不规则图形,学生不能熟练将不规则阴影部分面积转化为规则图形的面积进行计算,所以求阴影部分面积对学生来说是比较困难的,需要一次专门训练让学生体会求阴影部分面积的解题思路。
学习目标 (1)通过对求阴影部分面积问题的探究,会正确计算阴影部分的面积。 (2)通过计算,能归纳出求阴影部分面积的解题方法。
重难点 (1)通过对求阴影部分面积问题的探究,会正确计算阴影部分的面积。 (2)通过计算,能归纳出求阴影部分面积的解题方法。
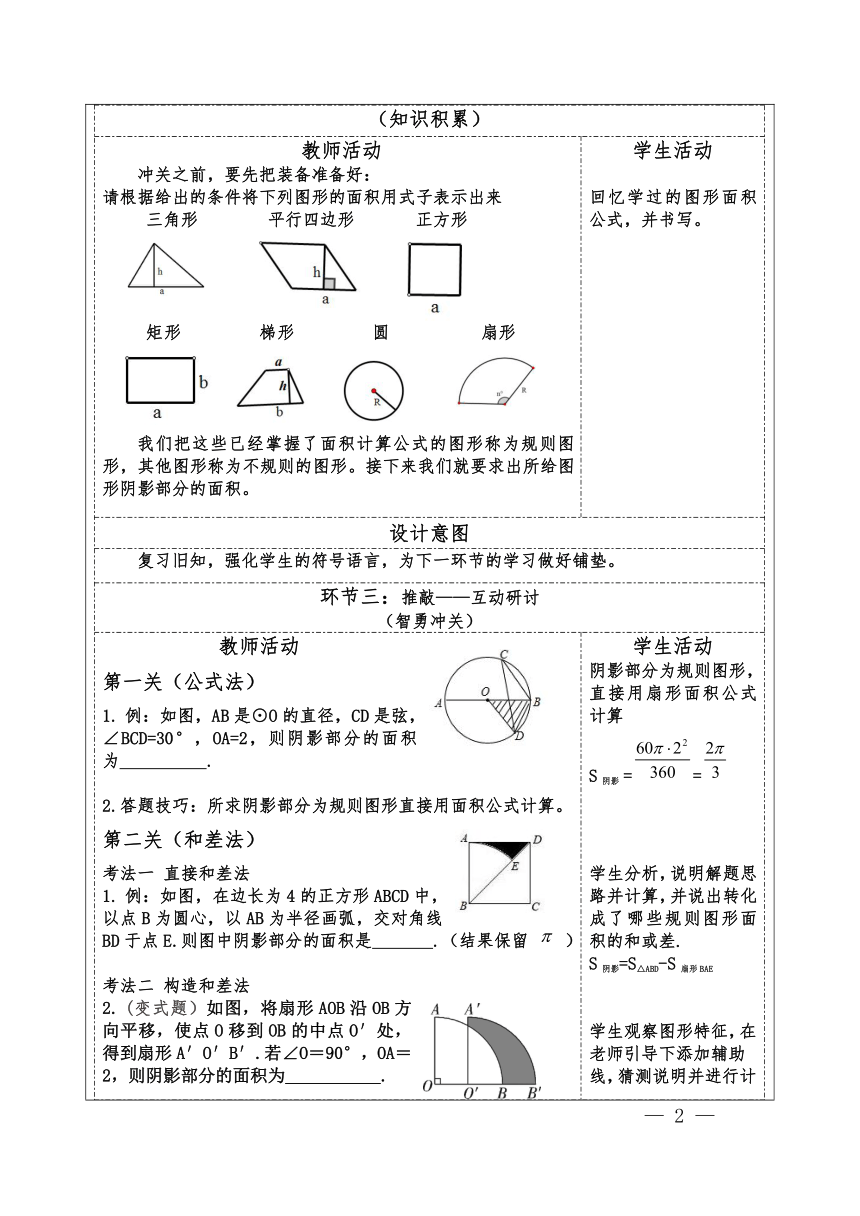
教学评活动过程 教师活动学生活动环节一:赋题——问题导入 (情境引入)形容一个人受到打击或者特别无奈的时候,大家经常会说一句:“求他的心理阴影面积。”说明求阴影面积的问题一直困扰着大家。那么如何求一个图形的阴影部分面积呢?今天我们一起走进课堂,各显神通,克服困难,“智勇大冲关”,看看能不能解决这个问题。出示学习目标。学生齐读目标 设计意图从学生熟悉的网络用语入手以及采用“智勇大冲关”的模式调动学生的学习兴趣,鼓励学生不怕困难、敢于解决难题。出示目标,让学生明确本节课的主要任务。环节二:立意——自学思探 (知识积累) 教师活动 冲关之前,要先把装备准备好: 请根据给出的条件将下列图形的面积用式子表示出来 三角形 平行四边形 正方形 矩形 梯形 圆 扇形 我们把这些已经掌握了面积计算公式的图形称为规则图形,其他图形称为不规则的图形。接下来我们就要求出所给图形阴影部分的面积。 学生活动 回忆学过的图形面积公式,并书写。 设计意图复习旧知,强化学生的符号语言,为下一环节的学习做好铺垫。环节三:推敲——互动研讨 (智勇冲关)教师活动 第一关(公式法) 例:如图,AB是⊙O的直径,CD是弦,∠BCD=30°,OA=2,则阴影部分的面积为 . 2.答题技巧:所求阴影部分为规则图形直接用面积公式计算。 第二关(和差法) 考法一 直接和差法 例:如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD于点E.则图中阴影部分的面积是 .(结果保留 ) 考法二 构造和差法 (变式题)如图,将扇形AOB沿OB方向平移,使点O移到OB的中点O′处,得到扇形A′O′B′.若∠O=90°,OA=2,则阴影部分的面积为 . 引导总结:构造图形时一般先观察阴影部分图形:若阴影部分图形有一部分是弧线,则关键是需要找出弧线所对应的圆心,连半径构造扇形。 3.答题技巧 当所求阴影部分为不规则图形且图形相对比较简单时,阴影部分面积可以直接看成扇形、三角形、特殊四边形的面积相加减;当所求阴影部分为不规则图形且图形相对比较复杂,不能直接看成规则图形的面积的和或差时,常通过“分割求和”“整体作差”等方法,添加适当的辅助线,构造扇形、三角形或特殊四边形,然后把它们的面积相加减。 第三关(等积转化法) 例:如图所示, O的直径AB=10cm,弦CD=EF=5cm,且CD//EF//AB,P为AB上的一点,图中阴影部分面积是 . (变式题)如图,扇形A0B的圆心角为90°,四边形OCDE是边长为1的正方形,点C,E,D分别在0A,OB及弧AB上,过点A作AF⊥ED,交ED的延长线于点F,图中阴影部分的面积 . 3.答题技巧: 当所求阴影部分的图形比较复杂,难以通过构造和差进行计算时,常利用等积转化的方法将其转化为求扇形、三角形、特殊四边形的面积或它们面积的和差。学生活动 阴影部分为规则图形,直接用扇形面积公式计算 S阴影 == 学生分析,说明解题思路并计算,并说出转化成了哪些规则图形面积的和或差. S阴影=S△ABD-S扇形BAE 学生观察图形特征,在老师引导下添加辅助线,猜测说明并进行计算。 设弧AB交A’O’于点C,连接OC,S阴影=S△OO’C+S扇形O’A’B’-S扇形OBC 学生先独立思考,同桌简单讨论,说出解题思路,并进行运算。 1.连接OC、OD、OE、OF S阴影=S扇形OCD+S扇形OEF 2.连接OD S阴影=S矩形ACDF 设计意图通过闯关由浅入深,由规则图形的面积计算到不规则图形面积计算,逐步渗透转化思想,让学生让学生对阴影部分面积的求解有个整体感知。环节四:共情——指导解惑 (勇攀高峰)教师活动 如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′,其中点B的运动路径为BB',则图中阴影部分的面积为 。 温馨提示:若阴影部分是由图形旋转构成,旋转中心即为圆心,将旋转前后的对应点分别与旋转中心连接构造扇形。 闯关感言: 鼓励学生畅所欲言。学生活动 学生思考,小组讨论,选代表展示 S阴影=S扇形DBB’-S梯形DCB’C’ 自由感言,总结求阴影部分的面积的解题技巧。设计意图通过小组交流合作作答,培养学生灵活运用所学的数学知识解决问题的能力及准确的语言表达能力。环节五:升华——巩固提高 (当堂检测)如图,正方形ABCD内接于 O, O的半径为2,以点A为圆心,以AC长为半径画弧交AB的延长线于点E,交AD的延长线于点F,图中阴影部分的面积是 . 2、如图,将圆心角为90°的扇形A0B和扇形COD叠放在一起,连接AC,BD.已知0A=3cm,OC=1cm,图中阴影部分的面积是_____.学生活动 学生独立完成设计意图通过检测让学生学以致用,强化记忆。
板书设计 求阴影部分的面积 转化 规则图形 不规则图形 公式法 和差法、等积变换法
特色学习资源分析、技术手段应用说明 运用作业单、希沃白板课件进行教学,用多媒体投屏进行习题展示,便于学生理解。
— 1 —
课时教学设计
课题 求阴影部分的面积
课型 新授课□ 复习课 试卷讲评课□ 其它课□
教学内容分析 面积问题是中学数学的重要内容之一,每年全国各省市中考数学试题中,都有求阴影部分面积问题。阴影部分面积问题主要涉及扇形面积、特殊图形(直角三角形、菱形、矩形、等边三角形)的性质与面积计算,试题灵活多变,对学生的计算能力也有一定的要求。因此,重视和加强阴影部分面积的解法技巧的教学是十分必要的。本节课通过引导学生独立思考、动手实践、自主探索与合作交流,使学生理解和掌握基本的求解阴影部分面积所用到的数学知识与答题技巧、转化的数学思想和方法,获得基本的数学活动经验,从而增强发现和提出问题的能力、分析和解决问题的能力。
学情分析 九年级学生已经学习圆的相关知识,会计算扇形的面积,其他规则几何图形的面积计算也有基础,但是一般来说要求的阴影部分图形是不规则图形,学生不能熟练将不规则阴影部分面积转化为规则图形的面积进行计算,所以求阴影部分面积对学生来说是比较困难的,需要一次专门训练让学生体会求阴影部分面积的解题思路。
学习目标 (1)通过对求阴影部分面积问题的探究,会正确计算阴影部分的面积。 (2)通过计算,能归纳出求阴影部分面积的解题方法。
重难点 (1)通过对求阴影部分面积问题的探究,会正确计算阴影部分的面积。 (2)通过计算,能归纳出求阴影部分面积的解题方法。
教学评活动过程 教师活动学生活动环节一:赋题——问题导入 (情境引入)形容一个人受到打击或者特别无奈的时候,大家经常会说一句:“求他的心理阴影面积。”说明求阴影面积的问题一直困扰着大家。那么如何求一个图形的阴影部分面积呢?今天我们一起走进课堂,各显神通,克服困难,“智勇大冲关”,看看能不能解决这个问题。出示学习目标。学生齐读目标 设计意图从学生熟悉的网络用语入手以及采用“智勇大冲关”的模式调动学生的学习兴趣,鼓励学生不怕困难、敢于解决难题。出示目标,让学生明确本节课的主要任务。环节二:立意——自学思探 (知识积累) 教师活动 冲关之前,要先把装备准备好: 请根据给出的条件将下列图形的面积用式子表示出来 三角形 平行四边形 正方形 矩形 梯形 圆 扇形 我们把这些已经掌握了面积计算公式的图形称为规则图形,其他图形称为不规则的图形。接下来我们就要求出所给图形阴影部分的面积。 学生活动 回忆学过的图形面积公式,并书写。 设计意图复习旧知,强化学生的符号语言,为下一环节的学习做好铺垫。环节三:推敲——互动研讨 (智勇冲关)教师活动 第一关(公式法) 例:如图,AB是⊙O的直径,CD是弦,∠BCD=30°,OA=2,则阴影部分的面积为 . 2.答题技巧:所求阴影部分为规则图形直接用面积公式计算。 第二关(和差法) 考法一 直接和差法 例:如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD于点E.则图中阴影部分的面积是 .(结果保留 ) 考法二 构造和差法 (变式题)如图,将扇形AOB沿OB方向平移,使点O移到OB的中点O′处,得到扇形A′O′B′.若∠O=90°,OA=2,则阴影部分的面积为 . 引导总结:构造图形时一般先观察阴影部分图形:若阴影部分图形有一部分是弧线,则关键是需要找出弧线所对应的圆心,连半径构造扇形。 3.答题技巧 当所求阴影部分为不规则图形且图形相对比较简单时,阴影部分面积可以直接看成扇形、三角形、特殊四边形的面积相加减;当所求阴影部分为不规则图形且图形相对比较复杂,不能直接看成规则图形的面积的和或差时,常通过“分割求和”“整体作差”等方法,添加适当的辅助线,构造扇形、三角形或特殊四边形,然后把它们的面积相加减。 第三关(等积转化法) 例:如图所示, O的直径AB=10cm,弦CD=EF=5cm,且CD//EF//AB,P为AB上的一点,图中阴影部分面积是 . (变式题)如图,扇形A0B的圆心角为90°,四边形OCDE是边长为1的正方形,点C,E,D分别在0A,OB及弧AB上,过点A作AF⊥ED,交ED的延长线于点F,图中阴影部分的面积 . 3.答题技巧: 当所求阴影部分的图形比较复杂,难以通过构造和差进行计算时,常利用等积转化的方法将其转化为求扇形、三角形、特殊四边形的面积或它们面积的和差。学生活动 阴影部分为规则图形,直接用扇形面积公式计算 S阴影 == 学生分析,说明解题思路并计算,并说出转化成了哪些规则图形面积的和或差. S阴影=S△ABD-S扇形BAE 学生观察图形特征,在老师引导下添加辅助线,猜测说明并进行计算。 设弧AB交A’O’于点C,连接OC,S阴影=S△OO’C+S扇形O’A’B’-S扇形OBC 学生先独立思考,同桌简单讨论,说出解题思路,并进行运算。 1.连接OC、OD、OE、OF S阴影=S扇形OCD+S扇形OEF 2.连接OD S阴影=S矩形ACDF 设计意图通过闯关由浅入深,由规则图形的面积计算到不规则图形面积计算,逐步渗透转化思想,让学生让学生对阴影部分面积的求解有个整体感知。环节四:共情——指导解惑 (勇攀高峰)教师活动 如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′,其中点B的运动路径为BB',则图中阴影部分的面积为 。 温馨提示:若阴影部分是由图形旋转构成,旋转中心即为圆心,将旋转前后的对应点分别与旋转中心连接构造扇形。 闯关感言: 鼓励学生畅所欲言。学生活动 学生思考,小组讨论,选代表展示 S阴影=S扇形DBB’-S梯形DCB’C’ 自由感言,总结求阴影部分的面积的解题技巧。设计意图通过小组交流合作作答,培养学生灵活运用所学的数学知识解决问题的能力及准确的语言表达能力。环节五:升华——巩固提高 (当堂检测)如图,正方形ABCD内接于 O, O的半径为2,以点A为圆心,以AC长为半径画弧交AB的延长线于点E,交AD的延长线于点F,图中阴影部分的面积是 . 2、如图,将圆心角为90°的扇形A0B和扇形COD叠放在一起,连接AC,BD.已知0A=3cm,OC=1cm,图中阴影部分的面积是_____.学生活动 学生独立完成设计意图通过检测让学生学以致用,强化记忆。
板书设计 求阴影部分的面积 转化 规则图形 不规则图形 公式法 和差法、等积变换法
特色学习资源分析、技术手段应用说明 运用作业单、希沃白板课件进行教学,用多媒体投屏进行习题展示,便于学生理解。
— 1 —
同课章节目录
