湖南省长沙市明德集团2025届高三上学期11月阶段检测数学试卷(含答案)
文档属性
| 名称 | 湖南省长沙市明德集团2025届高三上学期11月阶段检测数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-21 00:00:00 | ||
图片预览




文档简介
明德中学2025届高三11月阶段检测
数学试卷
满分:150分 时间:120分钟 命题:高三数学备课组 审题:高三数学备课组
第Ⅰ卷(选择题)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.对于集合A,B,定义集合,已知集合,F={0,3,4,5},则( )
A.{-1,0,2,3,4,5} B.{0,2,3,4,5} C.{-1,2,6} D.{-1,0,2,3,4}
2.已知i为虚数单位,复数,则( )
A. B. C. D.
3.若命题p:,,则命题p的否定为( )
A., B.,
C., D.,
4.已知直线和直线,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.函数的部分图象大致为( )
A. B.
C. D.
6.已知数列,中,,,,,若,则m=( )
A.4 B.5 C.6 D.7
7.牛顿冷却定律描述物体在常温环境下的温度变化:如果物体的初始温度为,则经过一定时间t分钟后的温度T满足,h称为半衰期,其中是环境温度.若,现有一杯80℃的热水降至75℃大约用时1分钟,那么水温从75℃降至45℃,大约还需要( )(参考数据:,)
A.11分钟 B.10分钟 C.9分钟 D.8分钟
8.已知函数,,若,则的最小值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9,若,下列说法正确的是( )
A.若,则 B.若,则
C.若,,则 D.若,则
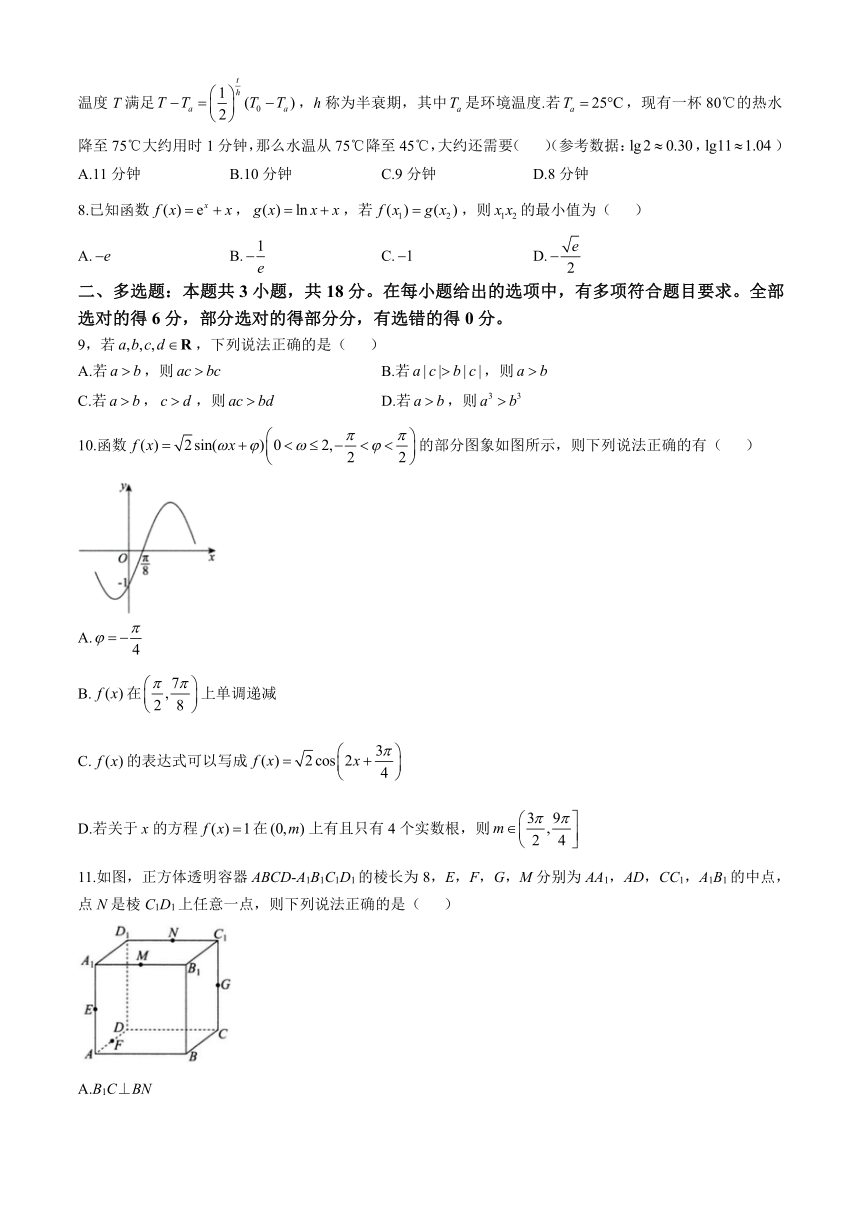
10.函数的部分图象如图所示,则下列说法正确的有( )
A.
B.在上单调递减
C.的表达式可以写成
D.若关于x的方程在上有且只有4个实数根,则
11.如图,正方体透明容器ABCD-A1B1C1D1的棱长为8,E,F,G,M分别为AA1,AD,CC1,A1B1的中点,点N是棱C1D1上任意一点,则下列说法正确的是( )
A.B1C⊥BN
B.向量在向量上的投影向量为
C.将容器的一个顶点放置于水平桌面上,使得正方体的12条棱所在的直线与桌面所成的角都相等,再向容器中注水,则注水过程中,容器内水面的最大面积为
D.向容器中装入直径为1的小球,最多可装入512个
第Ⅱ卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分。
12.若数列的前n项和为,且,则________.
13.已知椭圆C:,过左焦点F作直线l与圆M:相切于点E,与椭圆C在第一象限的交点为P,且,则椭圆离心率为________.
14.编号为1,2,3,4的四个小球,有放回地取三次,每次取一个,记m表示前两个球号码的平均数,记n表示三个球号码的平均数,则m与n之差的绝对值不超过0.2的概率是________.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)在锐角△ABC中,a,b,c分别是角A,B,C的对边,.
(1)求B;
(2)若,求△ABC的面积S取值范围.
16.(本小题15分)已知函数的导函数为,且.
(1)求函数在点处的切线方程;
(2)若对于任意的,恒成立,求实数m的取值范围.
17.(本小题15分)如图,三棱锥A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点.
(1)证明:BC⊥DA;
(2)点F满足,求平面ABD与平面ABF所成角的正弦值.
18.(本小题17分)椭圆经过点,其右焦点为抛物线的焦点F;
直线l与椭圆交于A,B两点,且以AB为直径的圆过原点.
(1)求椭圆的方程;
(2)若过原点的直线m与椭圆交于C,D两点,且,求四边形ACBD面积的最大值.
19.(本小题17分)n维向量是平面向量和空间向量的推广,对n维向量,记,设集合.
(1)求,;
(2)(ⅰ)求中元素的个数;
(ⅱ)记,求使得成立的最大正整数n.
明德中学2025届高三11月阶段检测(答案)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
题号 1 2 3 4 5 6 7 8
答案 C A D A A B B B
8.【答案】B【详解】∵,,,
∴,
令,,∴在R上单调递增,
∴,即,∴,
令,则,
当时,,单调递减;
当时,,单调递增;
∴当时,函数取得最小值,即,
∴,故选:B.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
题号 9 10 11
答案 BD ABD AC
11.解:由正方体性质知:B1C⊥BC1,B1C⊥DC1且都在面ABC1D1内,所以B1C⊥面ABC1D1,面ABC1D1,则B1C⊥BN,A对;
由题意EM//AB1且,若O是B1C,BC1交点,连接OG,
所以OG//BC//AF,,故AFGO为平行四边形,则AO//FG且AO=FG,
所以EM,FG所成角,即为AB1,AO所成角,
由题设,易知,,,
在△AOB1中,即AB1,AO夹角为,
所以EM,FG夹角为,故向量在向量上的投影向量为
,B错;
令放在桌面上的项点为A,若AC1⊥桌面时正方体的各棱所在的直线与桌面所成的角都相等,
此时要使容器内水的面积最大,即垂直于AC1的平面截正方体的截面积最大,
根据正方体的对称性,仅当截面过A1A1,BB1,BC,CD,DD1,A1D1中点时截面积最大,
此时,截面是边长为的正六边形,故最大面积为,C对;
由题意,第一层小球为8×8=64个,第二层小球为7×7=49,且奇数层均为64个,偶数层均为49,而第一层与第二层中任意四个相邻球的球心构成一个棱长为1的正四棱锥,故高为,假设共有n层小球,则总高度为,且n为正整数,
令,则,而,故小球总共有10层,由上,相邻的两层小球共有113个,所以正方体一共可以放113×5=565个小球,D错.故选:AC.
三、填空题:本题共3小题,每小题5分,共15分。
12.170 13. 14.
14.解:因为放回的抽取小球,所以基本事件总数为,
设抽取的前两个球的号码为a,b,第三个球的号码为c,
根据题意有,,则,
整理得,即,
当时,,此时为,,,3种情况;
当时,,此时为,,,,,,,,,9种情况;
当时,,此时为,,,,,,,,,9种情况;
当时,,此时为,,,3种情况;
综上得,满足条件的共有3+9+3+9=24,所以满足条件的概率为.
故答案为:.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
【答案】(1) (2)
解:(1)由,
由正弦定理,可得,
因为C为三角形内角,所以,所以,
得,
因为,所以,所以. 6分
(2)∵,故,
∴,
所以
,
因为,所以,
∴,∴,∴,
故△ABC的面积S的取值范围为. 13分
16.(本小题15分)
【答案】(1) (2)
解:(1)求导得,
令,则,∴,
∴,∴,
∴,即:. 5分
(2)方法一,,
①当时,左边右边,不等式显然成立.
②当时,
令,
当时,,,∴,在上单调递减
∴,∴.
③当时,
令,当时,,单调递减;
当时,,单调递增.
∴,∴
综上:m的取值范围为. 15分
法二,令,∴,
令,所以恒成立,∴在上递增.
①若,即对,
∴在单调递减,∴,∴,
与矛盾,∴无解,舍去.
②若,即,
,,∴在上递增
∴,∴.
故.
③若即:时,
使得,,即:
∴,
即:,
∵,∴,∴,∴,
∴,故综上.
17.(本小题15分)
【答案】(1)证明见解析(2)
解:(1)连接AE,DE,
因为E为BC中点,DB=DC,所以DE⊥BC①,
因为DA=DB=DC,∠ADB=∠ADC=60°,所以△ACD与△ABD均为等边三角形,
∴AC=AB,从而AE⊥BC②,
由①②,,AE,平面ADE,所以BC⊥平面ADE,
而平面ADE,所以BC⊥DA. 6分
(2)不妨设,
∵BD⊥CD,∴BC=2,DE=1,
则,即AC⊥AB,则AE=1,
∴,∴AE⊥DE,
又∵AE⊥BC,,平面BCD
∴AE⊥平面BCD,
以点E为原点,ED,EB,EA所在直线分别为x,y,z轴,建立空间直角坐标系,如图所示:
可得,,,,
设平面ABD与平面ABF的一个法向量分别为,,
平面ABD与平面ABF所成角为,而,,
因为,所以,即有,
可得,取,所以;
又,取,所以;
所以,从而,
所以平面ABD与平面ABF所成角的正弦值为. 15分
18.(本小题17分)
【答案】(1) (2)
解:点在椭圆上,即,
解得,,所以椭圆的方程为. 4分
(2)当直线AB斜率存在时,设其方程为,,
联立可得则①
②,③
以AB为直径的圆过原点即
化简可得,代入②③两式,
整理得即
将④式代入①式,得恒成立则
设线段AB中点为M,由,由观察可知,
,
又由,则C点坐标为,
化简可得,代回椭圆方程可得即
即,
另外,当直线AB斜率不存在时,AB方程为,直线CD过AB中点,即为x轴,
易得,,
综上,四边形ACBD面积的最大值为. 17分
19.(本小题17分)
【答案】(1),
(2)(ⅰ);(ⅱ)
解:(1)∵,
∴当时,;当时,;当时,;当时,,
∴,
∵,
当时,;当时,;当时,;当所时,;当时,;当时,;当时,;当时,,
∴. 4分
(2)(ⅰ)设中元素的个数为,
∵,,
∴为偶数时,,且,
∴
,
∴中的元素个数为. 9分
(ⅱ)①当时,
;
②当时,
;
③当时,
;
……;
要使得成立,其必要条件是当时,
,
令,则,
∴数列为递增数列,又,,
∴的解为;
当时,,即充分性成立;
∴使得成立的最大正整数. 17分
数学试卷
满分:150分 时间:120分钟 命题:高三数学备课组 审题:高三数学备课组
第Ⅰ卷(选择题)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.对于集合A,B,定义集合,已知集合,F={0,3,4,5},则( )
A.{-1,0,2,3,4,5} B.{0,2,3,4,5} C.{-1,2,6} D.{-1,0,2,3,4}
2.已知i为虚数单位,复数,则( )
A. B. C. D.
3.若命题p:,,则命题p的否定为( )
A., B.,
C., D.,
4.已知直线和直线,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.函数的部分图象大致为( )
A. B.
C. D.
6.已知数列,中,,,,,若,则m=( )
A.4 B.5 C.6 D.7
7.牛顿冷却定律描述物体在常温环境下的温度变化:如果物体的初始温度为,则经过一定时间t分钟后的温度T满足,h称为半衰期,其中是环境温度.若,现有一杯80℃的热水降至75℃大约用时1分钟,那么水温从75℃降至45℃,大约还需要( )(参考数据:,)
A.11分钟 B.10分钟 C.9分钟 D.8分钟
8.已知函数,,若,则的最小值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9,若,下列说法正确的是( )
A.若,则 B.若,则
C.若,,则 D.若,则
10.函数的部分图象如图所示,则下列说法正确的有( )
A.
B.在上单调递减
C.的表达式可以写成
D.若关于x的方程在上有且只有4个实数根,则
11.如图,正方体透明容器ABCD-A1B1C1D1的棱长为8,E,F,G,M分别为AA1,AD,CC1,A1B1的中点,点N是棱C1D1上任意一点,则下列说法正确的是( )
A.B1C⊥BN
B.向量在向量上的投影向量为
C.将容器的一个顶点放置于水平桌面上,使得正方体的12条棱所在的直线与桌面所成的角都相等,再向容器中注水,则注水过程中,容器内水面的最大面积为
D.向容器中装入直径为1的小球,最多可装入512个
第Ⅱ卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分。
12.若数列的前n项和为,且,则________.
13.已知椭圆C:,过左焦点F作直线l与圆M:相切于点E,与椭圆C在第一象限的交点为P,且,则椭圆离心率为________.
14.编号为1,2,3,4的四个小球,有放回地取三次,每次取一个,记m表示前两个球号码的平均数,记n表示三个球号码的平均数,则m与n之差的绝对值不超过0.2的概率是________.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)在锐角△ABC中,a,b,c分别是角A,B,C的对边,.
(1)求B;
(2)若,求△ABC的面积S取值范围.
16.(本小题15分)已知函数的导函数为,且.
(1)求函数在点处的切线方程;
(2)若对于任意的,恒成立,求实数m的取值范围.
17.(本小题15分)如图,三棱锥A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点.
(1)证明:BC⊥DA;
(2)点F满足,求平面ABD与平面ABF所成角的正弦值.
18.(本小题17分)椭圆经过点,其右焦点为抛物线的焦点F;
直线l与椭圆交于A,B两点,且以AB为直径的圆过原点.
(1)求椭圆的方程;
(2)若过原点的直线m与椭圆交于C,D两点,且,求四边形ACBD面积的最大值.
19.(本小题17分)n维向量是平面向量和空间向量的推广,对n维向量,记,设集合.
(1)求,;
(2)(ⅰ)求中元素的个数;
(ⅱ)记,求使得成立的最大正整数n.
明德中学2025届高三11月阶段检测(答案)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
题号 1 2 3 4 5 6 7 8
答案 C A D A A B B B
8.【答案】B【详解】∵,,,
∴,
令,,∴在R上单调递增,
∴,即,∴,
令,则,
当时,,单调递减;
当时,,单调递增;
∴当时,函数取得最小值,即,
∴,故选:B.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
题号 9 10 11
答案 BD ABD AC
11.解:由正方体性质知:B1C⊥BC1,B1C⊥DC1且都在面ABC1D1内,所以B1C⊥面ABC1D1,面ABC1D1,则B1C⊥BN,A对;
由题意EM//AB1且,若O是B1C,BC1交点,连接OG,
所以OG//BC//AF,,故AFGO为平行四边形,则AO//FG且AO=FG,
所以EM,FG所成角,即为AB1,AO所成角,
由题设,易知,,,
在△AOB1中,即AB1,AO夹角为,
所以EM,FG夹角为,故向量在向量上的投影向量为
,B错;
令放在桌面上的项点为A,若AC1⊥桌面时正方体的各棱所在的直线与桌面所成的角都相等,
此时要使容器内水的面积最大,即垂直于AC1的平面截正方体的截面积最大,
根据正方体的对称性,仅当截面过A1A1,BB1,BC,CD,DD1,A1D1中点时截面积最大,
此时,截面是边长为的正六边形,故最大面积为,C对;
由题意,第一层小球为8×8=64个,第二层小球为7×7=49,且奇数层均为64个,偶数层均为49,而第一层与第二层中任意四个相邻球的球心构成一个棱长为1的正四棱锥,故高为,假设共有n层小球,则总高度为,且n为正整数,
令,则,而,故小球总共有10层,由上,相邻的两层小球共有113个,所以正方体一共可以放113×5=565个小球,D错.故选:AC.
三、填空题:本题共3小题,每小题5分,共15分。
12.170 13. 14.
14.解:因为放回的抽取小球,所以基本事件总数为,
设抽取的前两个球的号码为a,b,第三个球的号码为c,
根据题意有,,则,
整理得,即,
当时,,此时为,,,3种情况;
当时,,此时为,,,,,,,,,9种情况;
当时,,此时为,,,,,,,,,9种情况;
当时,,此时为,,,3种情况;
综上得,满足条件的共有3+9+3+9=24,所以满足条件的概率为.
故答案为:.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
【答案】(1) (2)
解:(1)由,
由正弦定理,可得,
因为C为三角形内角,所以,所以,
得,
因为,所以,所以. 6分
(2)∵,故,
∴,
所以
,
因为,所以,
∴,∴,∴,
故△ABC的面积S的取值范围为. 13分
16.(本小题15分)
【答案】(1) (2)
解:(1)求导得,
令,则,∴,
∴,∴,
∴,即:. 5分
(2)方法一,,
①当时,左边右边,不等式显然成立.
②当时,
令,
当时,,,∴,在上单调递减
∴,∴.
③当时,
令,当时,,单调递减;
当时,,单调递增.
∴,∴
综上:m的取值范围为. 15分
法二,令,∴,
令,所以恒成立,∴在上递增.
①若,即对,
∴在单调递减,∴,∴,
与矛盾,∴无解,舍去.
②若,即,
,,∴在上递增
∴,∴.
故.
③若即:时,
使得,,即:
∴,
即:,
∵,∴,∴,∴,
∴,故综上.
17.(本小题15分)
【答案】(1)证明见解析(2)
解:(1)连接AE,DE,
因为E为BC中点,DB=DC,所以DE⊥BC①,
因为DA=DB=DC,∠ADB=∠ADC=60°,所以△ACD与△ABD均为等边三角形,
∴AC=AB,从而AE⊥BC②,
由①②,,AE,平面ADE,所以BC⊥平面ADE,
而平面ADE,所以BC⊥DA. 6分
(2)不妨设,
∵BD⊥CD,∴BC=2,DE=1,
则,即AC⊥AB,则AE=1,
∴,∴AE⊥DE,
又∵AE⊥BC,,平面BCD
∴AE⊥平面BCD,
以点E为原点,ED,EB,EA所在直线分别为x,y,z轴,建立空间直角坐标系,如图所示:
可得,,,,
设平面ABD与平面ABF的一个法向量分别为,,
平面ABD与平面ABF所成角为,而,,
因为,所以,即有,
可得,取,所以;
又,取,所以;
所以,从而,
所以平面ABD与平面ABF所成角的正弦值为. 15分
18.(本小题17分)
【答案】(1) (2)
解:点在椭圆上,即,
解得,,所以椭圆的方程为. 4分
(2)当直线AB斜率存在时,设其方程为,,
联立可得则①
②,③
以AB为直径的圆过原点即
化简可得,代入②③两式,
整理得即
将④式代入①式,得恒成立则
设线段AB中点为M,由,由观察可知,
,
又由,则C点坐标为,
化简可得,代回椭圆方程可得即
即,
另外,当直线AB斜率不存在时,AB方程为,直线CD过AB中点,即为x轴,
易得,,
综上,四边形ACBD面积的最大值为. 17分
19.(本小题17分)
【答案】(1),
(2)(ⅰ);(ⅱ)
解:(1)∵,
∴当时,;当时,;当时,;当时,,
∴,
∵,
当时,;当时,;当时,;当所时,;当时,;当时,;当时,;当时,,
∴. 4分
(2)(ⅰ)设中元素的个数为,
∵,,
∴为偶数时,,且,
∴
,
∴中的元素个数为. 9分
(ⅱ)①当时,
;
②当时,
;
③当时,
;
……;
要使得成立,其必要条件是当时,
,
令,则,
∴数列为递增数列,又,,
∴的解为;
当时,,即充分性成立;
∴使得成立的最大正整数. 17分
同课章节目录
