8.1数学广角-数与形(同步讲义)六年级数学上册人教版
文档属性
| 名称 | 8.1数学广角-数与形(同步讲义)六年级数学上册人教版 |  | |
| 格式 | doc | ||
| 文件大小 | 417.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-22 08:00:39 | ||
图片预览



文档简介
/ 让教学更有效 精品试卷 | 数学学科
8.1数学广角-数与形
(知识梳理+专项练习)
知识点一、算术中的规律
在数学算式中探索规律,应认真观察算式的特点,再观察结果的特点,进而,根据规律填出这一类算式的结果.
例如:1×1=1;
11×11=121;
111×111=12321;
1111×1111=1234321;
通过观察发现:每个算式中,两个因数各个数位上的数字都是1,且个数相同.积里的数字呈对称形式,且前半部分是从1开始,写至某个数字(此数即因数的位数),积的后半部分再顺次写出.
①一个数乘11,101的规律
一个数乘11的规律:可采用“两头一拉,中间相加”的方法计算.
如:123×11=1353
一个数乘101的规律:可采用“两两一位,隔位一加”的方法计算.
如:58734×101=5932134
②一个数乘5,15,25,125的规律
一个数乘5,转化为一个数乘10,然后,再除以2.
如:28×5=28×10÷2=280÷2=140
这种情况可以概括为“添0求半”.根据同级运算可交换位置的性质,也可以先除以2,再乘10.
如:28×5=28÷2×10=14×10=140.即“求半添0”的方法.
一个数乘15,可分解为先用这个数乘10,再加上这个数乘5,乘5的方法同上.
如:264×15=264×10+264×5=2640+264×10÷2=2640+2640÷2=2640+1320=3960.
这种情况可以概括为“添0补半”
一个数乘125,因为125×8=1000,所以,可将一个数乘125转化为先乘1000,再除以8,或先除以8,再乘1000.
如:864×125=864×1000÷8=864000÷8=108000.
知识点二、数列中的规律
按一定的次序排列的一列数,叫做数列.
(1)规律蕴涵在相邻两数的差或倍数中.
例如:1,2,3,4,5,6…相邻的差都为1;
1,2,4,8,16,32…相邻的两数为2倍关系.
(2)前后几项为一组,以组为单位找关系,便于找到规律.
例如:1,0,0,1,1,0,0,1…从左到右,每四项为一组;
1,2,3,5,8,13,21…规律为,从第三个数开始,每个数都是它前面两个数的和.
(3)需将数列本身分解,通过对比,发现规律.
例如,12,15,17,30,22,45,27,60…在这里,第1,3,5…项依次相差5,第2,4,6…项依次相差15.
(4)相邻两数的关系中隐含着规律.
例如,18,20,24,30,38,48,60…相邻两数依次差2,4,6,8,10,12…
知识点三、“式”的规律知
把一些算式排列在一起,从中发现规律,也是探索规律的重要内容.在探索“式”的规律时,要从组成“式”的要素中去探索.
知识点四、数与形结合的规律
在探索数与形结合的规律时,一方面要考虑图形的对称(上下对称和左右对称),另一方面要考虑数的排列规律,通过数形结合、对应等方法,来解决问题.
一、选择题
1.照下图这样画下去,第10个图形有( )个●。
A.54 B.55 C.56
2.有一数列:、、、、......第8个数是( ).
A. B. C. D.
3.由“某出版集团”出版的《挑战名牌初中》一书共230页,那么编页码时需要的数码总数是( )
A.700 B.582 C.577 D.230
二、填空题
4.找出下面数列的规律,然后填空。
100,81,64,( ),36,25,( ),9,4,1。
5.观察下图,一张桌子可以坐4人,两张桌子拼在一起可以坐6人,三张桌子拼起来可以坐8人,5张桌子拼起来可以坐( )人,38人需要( )张桌子拼起来。
6.一张正方形桌坐4个人(每个圆圈表示1个人),两张桌子排在一起能坐6个人,按照这样的规律,8张桌子排在一起,能坐( )个人。21教育网
7.照下面的方法摆三角形,摆1个需要3根小棒,摆2个需要5根小棒,摆3个需要7根小棒,摆10个需要( )根小棒。【版权所有:21教育】
三、判断题
8.3个人互相打电话,每2个人都要通,一共要通话6次。( )
9.一个数列为:1,2,3,1,2,3,…按这样的顺序排下去,第20个数是3.
10.8个点可以连成20条线段。( )
四、计算题
11.直接写出得数。
28.5-0.85 2.4+1.2÷4=
9×70%= 1+3+5+7+9+…+21=
五、解答题
12.用同样大小的黑色棋子按如图所示的规律摆放:
①第5个图形中有多少颗黑色棋子?
②第几个图形中有2013颗黑色棋子?
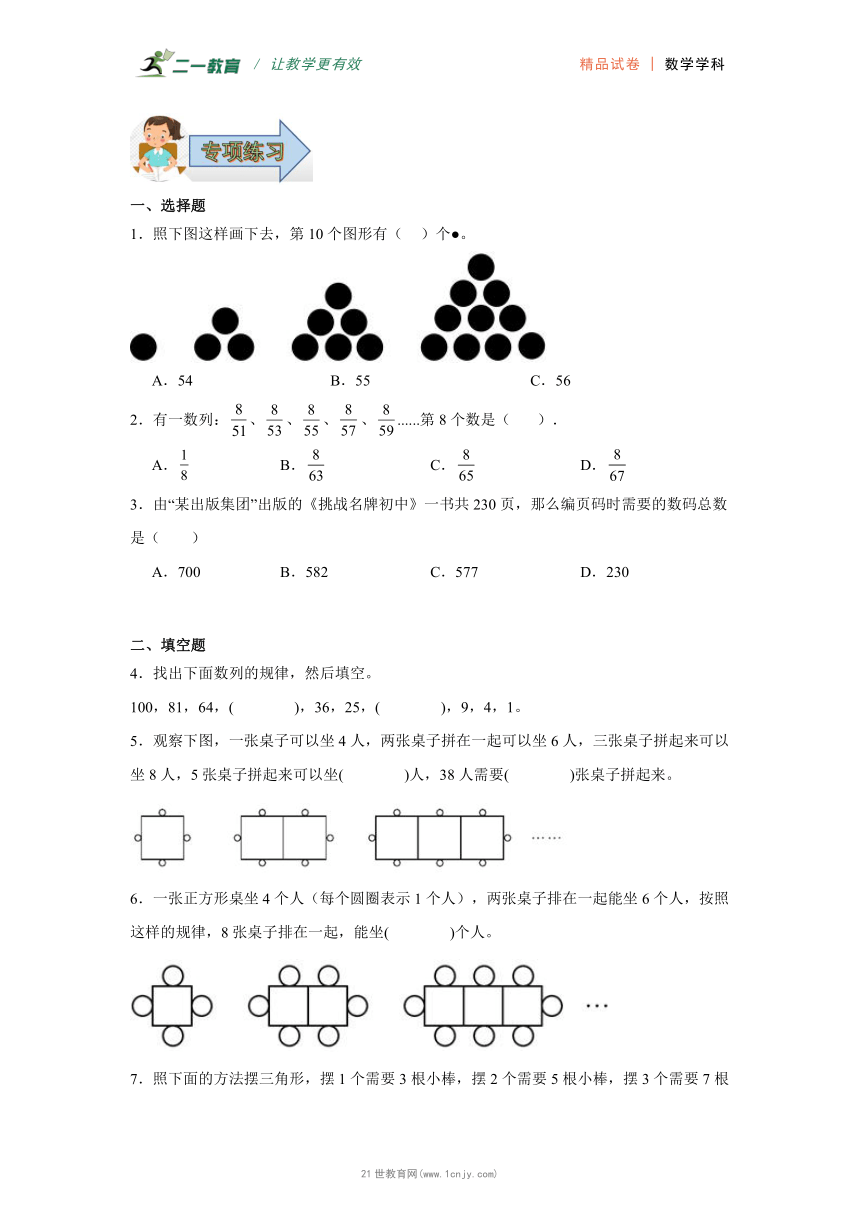
13.下面都是由边长为1厘米的小正方形拼成的大正方形。
① ② ③
(1)观察图形,完成表格。
图号 ① ② ③ ④ …
阴影部分边长(厘米) 1 2 3 …
最外圈正方形个数(个) 8 12 16
(2)以此类推,如果在图⑩的阴影部分内画一个最大的圆,这个圆的面积是多少?
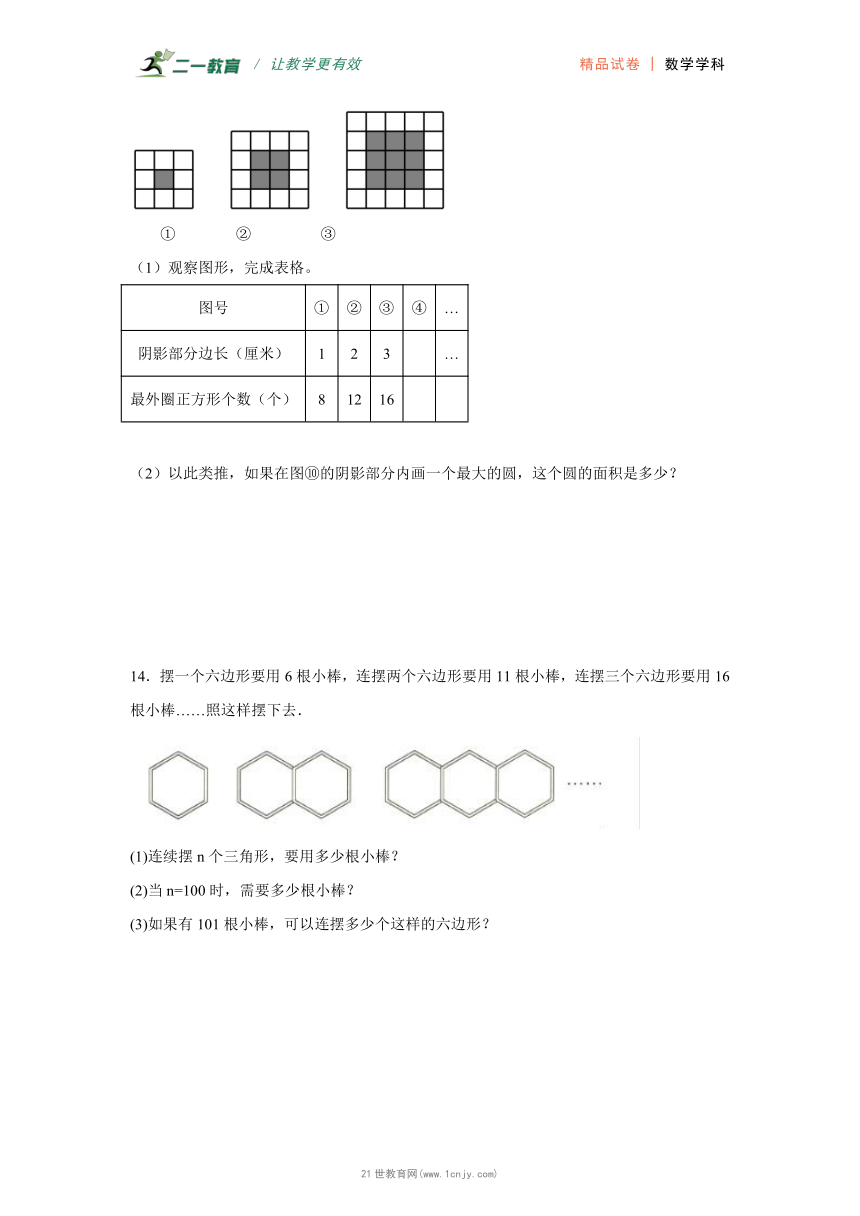
14.摆一个六边形要用6根小棒,连摆两个六边形要用11根小棒,连摆三个六边形要用16根小棒……照这样摆下去.21世纪教育网版权所有
(1)连续摆n个三角形,要用多少根小棒?
(2)当n=100时,需要多少根小棒?
(3)如果有101根小棒,可以连摆多少个这样的六边形?
15.如图,将一张正方形纸片剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去。2·1·c·n·j·y
(1)填表:
剪的次数 1 2 3 4 5
正方形个数
(2)如果剪了20次,共剪出多少个小正方形?
(3)观察图形,你还能发现什么规律?
16.小明把巧克力棒摆成了如图所示的形状,其中每一条小短边代表一个巧克力棒。请问:
(1)一共有多少个巧克力棒?
(2)这些巧克力棒共构成了多少个三角形?
(3)嘴馋的小明吃掉一个巧克力棒后(图中两端带有箭头的小边),剩下的图形中还有多少个三角形?
参考答案:
题号 1 2 3
答案 B C B
1.B
【解析】第1个图形有1个●;
第2个图形有1+2个●;
第3个图形有1+2+3个●;
第4个图形有1+2+3+4个●;
第n个图形有1+2+3+4+……+n个●;
据此解答。
【详解】1+2+3+4+5+6+7+8+9+10
=(1+10)×5
=11×5
=55(个)
第10个图形有55个●。
故选:B。
【点睛】根据前四个图形找出规律,再根据规律来解答问题。
2.C
【详解】略
3.B
【分析】本题可根据自然数的排列规律及数位知识进行分析.
【详解】在1~230中,个位数共有9个,需要数码9个;
两位数共有90个,需要数码90×2=180个;
三位数共有131个,需要数码131×3=393个;
共需要数码:9+180+393=582(个).
即编页码时需要的数码总数是582个.
4. 49 16
【分析】100可以看成10乘10,81可以看成9乘9,64可以看成8乘8,36可以看成6乘6,数列中的每一个数依次是10、9、8、7、6、5、4、3、2、1的平方。
【详解】
【点睛】本题也可以根据相邻两个数的差进行推理,相邻两个数的差分别是19、17、15、13、11、9、7、5、3,构成等差数列。21·世纪*教育网
5. 12 18
【分析】由图示可知,一张桌子可以坐4人,两张桌子增加了2人,可以坐6人;3张桌子又增加了2人,可以坐8人;以此类推,则第n张桌子可以坐(2n+2)人。可令n=5,即可求出5张桌子拼起来能坐多少人;再令2n+2=38,解这个方程,即可求出38人需要几张桌子拼起来。www-2-1-cnjy-com
【详解】一张桌子 4人
两张桌子 6人
三张桌子 8人
四张桌子 4+3×2
n张桌子 4+(n-1)×2=4+2n-2=2n+2(人)
令n=5,
2n+2
=2×5+2
=10+2
=12(人)
解:设38人需要x张桌子拼起来,
2n+2=38
2n=36
n=18
【点睛】可先根据题意总结出桌子的张数与可坐人数的一般关系式,再代入问题中桌子的张数,求代数式的值;最后套用关系式,用解方程的办法计算出需要几张桌子。
6.18
【分析】观察三个图形得到一张正方形桌子可坐4人,二张正方形桌子可坐(4+2×1)人,则每增加一个桌子就可多坐两个人,于是得到n张正方形桌子可坐[4+2(n-1)]人。
【详解】由分析可得:
4+2×(8-1)
=4+2×7
=4+14
=18(人)
【点睛】本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况。21*cnjy*com
7.21
【解析】略
8.×
【分析】由于每个同学都要和另外的2个通一次电话,一共要通:3×2=6(次);又因为两个同学只通一次电话,去掉重复计算的情况,实际只通:6÷2=3(次),据此解答。
【详解】(3-1)×3÷2
=6÷2
=3(次)
则一共要通话3次。故原题干说法错误。
故答案为:×
【点睛】本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果人比较少可以用枚举法解答,如果人数比较多可以用公式:通话次数=人数(人数-1)÷2解答。
9.×
【详解】20÷3=6(组)…2(个)
每组中的第2个是2,所以第20个数是2.
故答案为×
10.×
【分析】3个点连成线段的条数: 1+2=3(条),4个点连成线段的条数:1+2+3=6(条),5个点连成线段的条数: 1+2+3+4=10(条),由此得出规律:n个点的线段数是: 1+2+3+4+……+ n-1条线段,据此规律解答即可。21cnjy.com
【详解】8个点可以连成线段数为1+2+3+4+5+6+7=28(条),所以本题说法错误。
故答案为:×
【点睛】本题考查探索规律,解答本题的关键是根据数形结合的思想,在草稿纸上画出几个点,然后得出规律,根据规律解答问题。21教育名师原创作品
11.27.65;0.5;2.7;;
0.25;6.3;;121;
【详解】略。
12.①18颗
②第670个图形
【分析】观察图形可知,后一个图形中黑色棋子数比前一个多3,由此可得出第n个图形有3(n+1)个棋子,据此解答。21*cnjy*com
【详解】①3×(5+1)
=3×6
=18(颗)
答:第5个图形中有18颗黑色棋子。
②解:设第x个图形中有2013颗黑色棋子。
3x+3=2013
x=670
答:第670个图形中有2013个棋子。
【点睛】此题主要考查了数与形,找出图形的变化规律是解题关键。
13.(1)见详解;(2)78.5平方厘米
【分析】(1)观察题意可知,图①的最外圈正方形个数=4×2,图②的最外圈正方形个数=4×3,图③的最外圈正方形个数=4×4,……,据此推出图n的最外圈正方形个数=4×(n+1),因为图号和对应的阴影部分边长的厘米数相等,所以图n的阴影部分的边长为n厘米,据此求出图④的最外圈正方形个数和图④的阴影部分边长。
(2)观察题意可知,图⑩的阴影部分边长为10厘米,要在这个正方形内画一个最大的圆,则圆的直径是10厘米,根据圆面积公式:S=πr2,用3.14×(10÷2)2即可求出这个圆的面积。
【详解】(1)图①的最外圈正方形个数:8=4×2
图②的最外圈正方形个数:12=4×3
图③的最外圈正方形个数:16=4×4
……
图n的最外圈正方形个数:4×(n+1)=(4n+4)个
因为图号和对应的阴影部分边长的厘米数相等,
所以图n的阴影部分的边长为n厘米,
当n=4时,
4×4+4
=16+4
=20(个)
图④的阴影部分边长为4厘米,最外圈正方形个数为20个。
如下表:
图号 ① ② ③ ④ …
阴影部分边长(厘米) 1 2 3 4 …
最外圈正方形个数(个) 8 12 16 20 …
(2)图⑩的阴影部分边长为10厘米,
3.14×(10÷2)2
=3.14×52
=3.14×25
=78.5(平方厘米)
答:如果在图⑩的阴影部分内画一个最大的圆,这个圆的面积是78.5平方厘米。
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
14.(1)(5n+1)根 (2)501根 (3)20个
【详解】(1)(5n+1)根
(2)n=100时,5n+1=5×100+1=501(根)
(3)5n+1=101
5n=100
n=20
即可以连摆20个这样的六边形.
15.(1)见详解;
(2)61个;
(3)见详解
【分析】(1)剪1次时,这大正方形被分成4个小正方形,第2次将其中的一个小正方形再剪成4个小正方形,此时正方形的个数是4+3=7个,第3次,再在第2次的基础上将其中的一个最小的正方形剪成4个更小的正方形,那么此时正方形的个数是3+3+4=10个,由此可知每剪一次,正方形的个数在前一次的基础上增加3个,据此给10加3即可求出第4次共有13个正方形,第5次在第4次的基础上增加3个正方形,此时正方形的个数是13+3=16个。21·cn·jy·com
(2)根据(1)中表格的数据,剪出的正方形个数是次数的3倍多1,求剪20次时剪出小正方形的个数,给20乘3,再加1即可求出个数。www.21-cn-jy.com
(3)根据剪出的正方形个数与剪的次数的关系,可以总结剪了n次后,把小正方形的个数用含n的式子来表示。【来源:21·世纪·教育·网】
【详解】(1)3+4=7(个)
7+3=10(个)
10+3=13(个)
13+3=16(个)
剪的次数 1 2 3 4 5
正方形个数/个 4 7 10 13 16
(2)20×3+1
=60+1
=61(个)
答:如果剪了20次,共剪出61个小正方形。
(3)答:我发现每剪一次会比上一次多3个正方形,如果剪n次,正方形的个数为3n+1。
16.(1)30个(2)27个(3)22个
【分析】(1)从上往下数出巧克力棒的个数即可求解;
(2)观察图形:①三角形顶点向上的三角形个数:以一个巧克力棒为边的三角形有:1+2+3+4=10个;以两个巧克力棒为边的有:1+2+3=6个;以3个巧克力棒为边的三角形有:1+2=3个;以4个巧克力棒为边的三角形有1个;2-1-c-n-j-y
②三角形顶点向下的有:以1个巧克力棒为边的三角形有:1+2+3=6个;以两个巧克力棒为边的三角形有:1个。由此利用加法原理即可求得图中的三角形个数;
(3)先数出嘴馋的小明吃掉一个巧克力棒后减少的三角形的个数,再相减即可求解。
【详解】(1)(1+2+3+4)×3
=10×3
=30(个)
答:一共有30个巧克力棒。
(2)根据题干分析可得:
①三角形顶点向上的三角形个数:以一个巧克力棒为边的三角形有:1+2+3+4=10个;以两个巧克力棒为边的有:1+2+3=6个;以3个巧克力棒为边的三角形有:1+2=3个;以4个巧克力棒为边的三角形有1个;【来源:21cnj*y.co*m】
②三角形顶点向下的有:以1个巧克力棒为边的三角形有:1+2+3=6个;以两个巧克力棒为边的三角形有:1个。共构成了10+6+3+1+6+1=27(个)【出处:21教育名师】
答:这些巧克力棒共构成了27个三角形。
(3)27﹣(2+2+1)
=27﹣5
=22(个)
答:剩下的图形中还有22个三角形。
【点睛】考查了组合图形的计数。此类问题,要分类进行计数,避免重复或漏缺。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
8.1数学广角-数与形
(知识梳理+专项练习)
知识点一、算术中的规律
在数学算式中探索规律,应认真观察算式的特点,再观察结果的特点,进而,根据规律填出这一类算式的结果.
例如:1×1=1;
11×11=121;
111×111=12321;
1111×1111=1234321;
通过观察发现:每个算式中,两个因数各个数位上的数字都是1,且个数相同.积里的数字呈对称形式,且前半部分是从1开始,写至某个数字(此数即因数的位数),积的后半部分再顺次写出.
①一个数乘11,101的规律
一个数乘11的规律:可采用“两头一拉,中间相加”的方法计算.
如:123×11=1353
一个数乘101的规律:可采用“两两一位,隔位一加”的方法计算.
如:58734×101=5932134
②一个数乘5,15,25,125的规律
一个数乘5,转化为一个数乘10,然后,再除以2.
如:28×5=28×10÷2=280÷2=140
这种情况可以概括为“添0求半”.根据同级运算可交换位置的性质,也可以先除以2,再乘10.
如:28×5=28÷2×10=14×10=140.即“求半添0”的方法.
一个数乘15,可分解为先用这个数乘10,再加上这个数乘5,乘5的方法同上.
如:264×15=264×10+264×5=2640+264×10÷2=2640+2640÷2=2640+1320=3960.
这种情况可以概括为“添0补半”
一个数乘125,因为125×8=1000,所以,可将一个数乘125转化为先乘1000,再除以8,或先除以8,再乘1000.
如:864×125=864×1000÷8=864000÷8=108000.
知识点二、数列中的规律
按一定的次序排列的一列数,叫做数列.
(1)规律蕴涵在相邻两数的差或倍数中.
例如:1,2,3,4,5,6…相邻的差都为1;
1,2,4,8,16,32…相邻的两数为2倍关系.
(2)前后几项为一组,以组为单位找关系,便于找到规律.
例如:1,0,0,1,1,0,0,1…从左到右,每四项为一组;
1,2,3,5,8,13,21…规律为,从第三个数开始,每个数都是它前面两个数的和.
(3)需将数列本身分解,通过对比,发现规律.
例如,12,15,17,30,22,45,27,60…在这里,第1,3,5…项依次相差5,第2,4,6…项依次相差15.
(4)相邻两数的关系中隐含着规律.
例如,18,20,24,30,38,48,60…相邻两数依次差2,4,6,8,10,12…
知识点三、“式”的规律知
把一些算式排列在一起,从中发现规律,也是探索规律的重要内容.在探索“式”的规律时,要从组成“式”的要素中去探索.
知识点四、数与形结合的规律
在探索数与形结合的规律时,一方面要考虑图形的对称(上下对称和左右对称),另一方面要考虑数的排列规律,通过数形结合、对应等方法,来解决问题.
一、选择题
1.照下图这样画下去,第10个图形有( )个●。
A.54 B.55 C.56
2.有一数列:、、、、......第8个数是( ).
A. B. C. D.
3.由“某出版集团”出版的《挑战名牌初中》一书共230页,那么编页码时需要的数码总数是( )
A.700 B.582 C.577 D.230
二、填空题
4.找出下面数列的规律,然后填空。
100,81,64,( ),36,25,( ),9,4,1。
5.观察下图,一张桌子可以坐4人,两张桌子拼在一起可以坐6人,三张桌子拼起来可以坐8人,5张桌子拼起来可以坐( )人,38人需要( )张桌子拼起来。
6.一张正方形桌坐4个人(每个圆圈表示1个人),两张桌子排在一起能坐6个人,按照这样的规律,8张桌子排在一起,能坐( )个人。21教育网
7.照下面的方法摆三角形,摆1个需要3根小棒,摆2个需要5根小棒,摆3个需要7根小棒,摆10个需要( )根小棒。【版权所有:21教育】
三、判断题
8.3个人互相打电话,每2个人都要通,一共要通话6次。( )
9.一个数列为:1,2,3,1,2,3,…按这样的顺序排下去,第20个数是3.
10.8个点可以连成20条线段。( )
四、计算题
11.直接写出得数。
28.5-0.85 2.4+1.2÷4=
9×70%= 1+3+5+7+9+…+21=
五、解答题
12.用同样大小的黑色棋子按如图所示的规律摆放:
①第5个图形中有多少颗黑色棋子?
②第几个图形中有2013颗黑色棋子?
13.下面都是由边长为1厘米的小正方形拼成的大正方形。
① ② ③
(1)观察图形,完成表格。
图号 ① ② ③ ④ …
阴影部分边长(厘米) 1 2 3 …
最外圈正方形个数(个) 8 12 16
(2)以此类推,如果在图⑩的阴影部分内画一个最大的圆,这个圆的面积是多少?
14.摆一个六边形要用6根小棒,连摆两个六边形要用11根小棒,连摆三个六边形要用16根小棒……照这样摆下去.21世纪教育网版权所有
(1)连续摆n个三角形,要用多少根小棒?
(2)当n=100时,需要多少根小棒?
(3)如果有101根小棒,可以连摆多少个这样的六边形?
15.如图,将一张正方形纸片剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去。2·1·c·n·j·y
(1)填表:
剪的次数 1 2 3 4 5
正方形个数
(2)如果剪了20次,共剪出多少个小正方形?
(3)观察图形,你还能发现什么规律?
16.小明把巧克力棒摆成了如图所示的形状,其中每一条小短边代表一个巧克力棒。请问:
(1)一共有多少个巧克力棒?
(2)这些巧克力棒共构成了多少个三角形?
(3)嘴馋的小明吃掉一个巧克力棒后(图中两端带有箭头的小边),剩下的图形中还有多少个三角形?
参考答案:
题号 1 2 3
答案 B C B
1.B
【解析】第1个图形有1个●;
第2个图形有1+2个●;
第3个图形有1+2+3个●;
第4个图形有1+2+3+4个●;
第n个图形有1+2+3+4+……+n个●;
据此解答。
【详解】1+2+3+4+5+6+7+8+9+10
=(1+10)×5
=11×5
=55(个)
第10个图形有55个●。
故选:B。
【点睛】根据前四个图形找出规律,再根据规律来解答问题。
2.C
【详解】略
3.B
【分析】本题可根据自然数的排列规律及数位知识进行分析.
【详解】在1~230中,个位数共有9个,需要数码9个;
两位数共有90个,需要数码90×2=180个;
三位数共有131个,需要数码131×3=393个;
共需要数码:9+180+393=582(个).
即编页码时需要的数码总数是582个.
4. 49 16
【分析】100可以看成10乘10,81可以看成9乘9,64可以看成8乘8,36可以看成6乘6,数列中的每一个数依次是10、9、8、7、6、5、4、3、2、1的平方。
【详解】
【点睛】本题也可以根据相邻两个数的差进行推理,相邻两个数的差分别是19、17、15、13、11、9、7、5、3,构成等差数列。21·世纪*教育网
5. 12 18
【分析】由图示可知,一张桌子可以坐4人,两张桌子增加了2人,可以坐6人;3张桌子又增加了2人,可以坐8人;以此类推,则第n张桌子可以坐(2n+2)人。可令n=5,即可求出5张桌子拼起来能坐多少人;再令2n+2=38,解这个方程,即可求出38人需要几张桌子拼起来。www-2-1-cnjy-com
【详解】一张桌子 4人
两张桌子 6人
三张桌子 8人
四张桌子 4+3×2
n张桌子 4+(n-1)×2=4+2n-2=2n+2(人)
令n=5,
2n+2
=2×5+2
=10+2
=12(人)
解:设38人需要x张桌子拼起来,
2n+2=38
2n=36
n=18
【点睛】可先根据题意总结出桌子的张数与可坐人数的一般关系式,再代入问题中桌子的张数,求代数式的值;最后套用关系式,用解方程的办法计算出需要几张桌子。
6.18
【分析】观察三个图形得到一张正方形桌子可坐4人,二张正方形桌子可坐(4+2×1)人,则每增加一个桌子就可多坐两个人,于是得到n张正方形桌子可坐[4+2(n-1)]人。
【详解】由分析可得:
4+2×(8-1)
=4+2×7
=4+14
=18(人)
【点睛】本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况。21*cnjy*com
7.21
【解析】略
8.×
【分析】由于每个同学都要和另外的2个通一次电话,一共要通:3×2=6(次);又因为两个同学只通一次电话,去掉重复计算的情况,实际只通:6÷2=3(次),据此解答。
【详解】(3-1)×3÷2
=6÷2
=3(次)
则一共要通话3次。故原题干说法错误。
故答案为:×
【点睛】本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果人比较少可以用枚举法解答,如果人数比较多可以用公式:通话次数=人数(人数-1)÷2解答。
9.×
【详解】20÷3=6(组)…2(个)
每组中的第2个是2,所以第20个数是2.
故答案为×
10.×
【分析】3个点连成线段的条数: 1+2=3(条),4个点连成线段的条数:1+2+3=6(条),5个点连成线段的条数: 1+2+3+4=10(条),由此得出规律:n个点的线段数是: 1+2+3+4+……+ n-1条线段,据此规律解答即可。21cnjy.com
【详解】8个点可以连成线段数为1+2+3+4+5+6+7=28(条),所以本题说法错误。
故答案为:×
【点睛】本题考查探索规律,解答本题的关键是根据数形结合的思想,在草稿纸上画出几个点,然后得出规律,根据规律解答问题。21教育名师原创作品
11.27.65;0.5;2.7;;
0.25;6.3;;121;
【详解】略。
12.①18颗
②第670个图形
【分析】观察图形可知,后一个图形中黑色棋子数比前一个多3,由此可得出第n个图形有3(n+1)个棋子,据此解答。21*cnjy*com
【详解】①3×(5+1)
=3×6
=18(颗)
答:第5个图形中有18颗黑色棋子。
②解:设第x个图形中有2013颗黑色棋子。
3x+3=2013
x=670
答:第670个图形中有2013个棋子。
【点睛】此题主要考查了数与形,找出图形的变化规律是解题关键。
13.(1)见详解;(2)78.5平方厘米
【分析】(1)观察题意可知,图①的最外圈正方形个数=4×2,图②的最外圈正方形个数=4×3,图③的最外圈正方形个数=4×4,……,据此推出图n的最外圈正方形个数=4×(n+1),因为图号和对应的阴影部分边长的厘米数相等,所以图n的阴影部分的边长为n厘米,据此求出图④的最外圈正方形个数和图④的阴影部分边长。
(2)观察题意可知,图⑩的阴影部分边长为10厘米,要在这个正方形内画一个最大的圆,则圆的直径是10厘米,根据圆面积公式:S=πr2,用3.14×(10÷2)2即可求出这个圆的面积。
【详解】(1)图①的最外圈正方形个数:8=4×2
图②的最外圈正方形个数:12=4×3
图③的最外圈正方形个数:16=4×4
……
图n的最外圈正方形个数:4×(n+1)=(4n+4)个
因为图号和对应的阴影部分边长的厘米数相等,
所以图n的阴影部分的边长为n厘米,
当n=4时,
4×4+4
=16+4
=20(个)
图④的阴影部分边长为4厘米,最外圈正方形个数为20个。
如下表:
图号 ① ② ③ ④ …
阴影部分边长(厘米) 1 2 3 4 …
最外圈正方形个数(个) 8 12 16 20 …
(2)图⑩的阴影部分边长为10厘米,
3.14×(10÷2)2
=3.14×52
=3.14×25
=78.5(平方厘米)
答:如果在图⑩的阴影部分内画一个最大的圆,这个圆的面积是78.5平方厘米。
【点睛】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题。
14.(1)(5n+1)根 (2)501根 (3)20个
【详解】(1)(5n+1)根
(2)n=100时,5n+1=5×100+1=501(根)
(3)5n+1=101
5n=100
n=20
即可以连摆20个这样的六边形.
15.(1)见详解;
(2)61个;
(3)见详解
【分析】(1)剪1次时,这大正方形被分成4个小正方形,第2次将其中的一个小正方形再剪成4个小正方形,此时正方形的个数是4+3=7个,第3次,再在第2次的基础上将其中的一个最小的正方形剪成4个更小的正方形,那么此时正方形的个数是3+3+4=10个,由此可知每剪一次,正方形的个数在前一次的基础上增加3个,据此给10加3即可求出第4次共有13个正方形,第5次在第4次的基础上增加3个正方形,此时正方形的个数是13+3=16个。21·cn·jy·com
(2)根据(1)中表格的数据,剪出的正方形个数是次数的3倍多1,求剪20次时剪出小正方形的个数,给20乘3,再加1即可求出个数。www.21-cn-jy.com
(3)根据剪出的正方形个数与剪的次数的关系,可以总结剪了n次后,把小正方形的个数用含n的式子来表示。【来源:21·世纪·教育·网】
【详解】(1)3+4=7(个)
7+3=10(个)
10+3=13(个)
13+3=16(个)
剪的次数 1 2 3 4 5
正方形个数/个 4 7 10 13 16
(2)20×3+1
=60+1
=61(个)
答:如果剪了20次,共剪出61个小正方形。
(3)答:我发现每剪一次会比上一次多3个正方形,如果剪n次,正方形的个数为3n+1。
16.(1)30个(2)27个(3)22个
【分析】(1)从上往下数出巧克力棒的个数即可求解;
(2)观察图形:①三角形顶点向上的三角形个数:以一个巧克力棒为边的三角形有:1+2+3+4=10个;以两个巧克力棒为边的有:1+2+3=6个;以3个巧克力棒为边的三角形有:1+2=3个;以4个巧克力棒为边的三角形有1个;2-1-c-n-j-y
②三角形顶点向下的有:以1个巧克力棒为边的三角形有:1+2+3=6个;以两个巧克力棒为边的三角形有:1个。由此利用加法原理即可求得图中的三角形个数;
(3)先数出嘴馋的小明吃掉一个巧克力棒后减少的三角形的个数,再相减即可求解。
【详解】(1)(1+2+3+4)×3
=10×3
=30(个)
答:一共有30个巧克力棒。
(2)根据题干分析可得:
①三角形顶点向上的三角形个数:以一个巧克力棒为边的三角形有:1+2+3+4=10个;以两个巧克力棒为边的有:1+2+3=6个;以3个巧克力棒为边的三角形有:1+2=3个;以4个巧克力棒为边的三角形有1个;【来源:21cnj*y.co*m】
②三角形顶点向下的有:以1个巧克力棒为边的三角形有:1+2+3=6个;以两个巧克力棒为边的三角形有:1个。共构成了10+6+3+1+6+1=27(个)【出处:21教育名师】
答:这些巧克力棒共构成了27个三角形。
(3)27﹣(2+2+1)
=27﹣5
=22(个)
答:剩下的图形中还有22个三角形。
【点睛】考查了组合图形的计数。此类问题,要分类进行计数,避免重复或漏缺。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
