余弦定理、正弦定理 课件(共56张PPT)-2025届高三数学一轮复习
文档属性
| 名称 | 余弦定理、正弦定理 课件(共56张PPT)-2025届高三数学一轮复习 |

|
|
| 格式 | zip | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-24 16:05:59 | ||
图片预览











文档简介
(共56张PPT)
高考数学一轮复习
余弦定理、正弦定理
◆ 知识聚焦 ◆
1. 正、余弦定理
在中,内角,,所对的边分别是,,,为 外接圆的半径,则
正弦定理 余弦定理
公 式 ;
;
正弦定理 余弦定理
常 见 变 形 , , ; #b# ,, ; #b# ; #b# , , #b# ;
;
续表
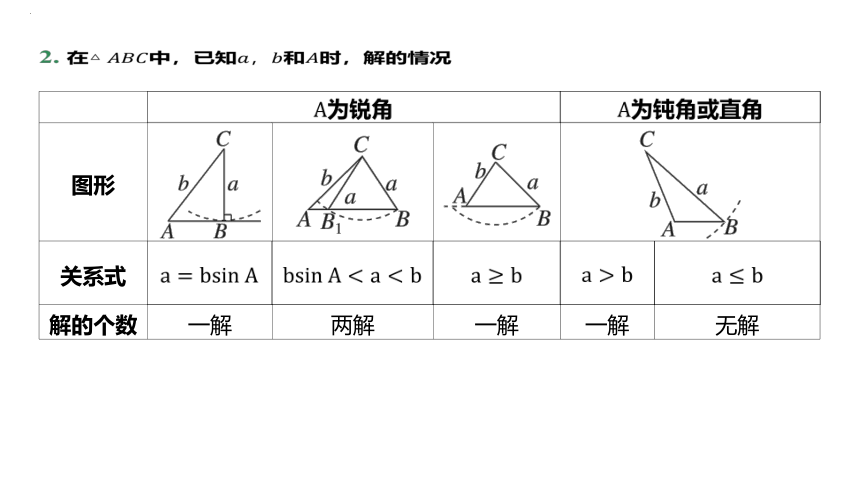
2. 在中,已知,和 时,解的情况
为锐角 为钝角或直角
图形
关系式
解的个数 一解 两解 一解 一解 无解
3. 面积公式
;
是的内切圆半径,是 的外接圆半
径,并可由此计算, .
常用结论
1.正弦定理的应用
①边化角,角化边 .
②大边对大角,大角对大边
.
③合分比:
是 的外接圆半径).
2.内角和定理: .
.
同理有:, .
.
③斜三角形中,
.
; .
⑤在中,内角,,成等差数列, .
◆ 对点演练 ◆
题组一 常识题
1. 在中,,,,则 _ ___.
[解析] 在中,设,, ,
则由余弦定理得,
因为为 的内角,所以 .
2. 已知的内角,,的对边分别为,,,若 的
面积为4,, ,则 ___.
8
[解析] 由,得 .
3. 在中,已知, , ,则边
_ _________.
[解析] ,
由正弦定理,得 ,得 .
4.[教材改编] 在中,内角,,的对边分别为,,,若 ,
且,则 ___.
[解析] 由余弦定理可得,化简整理得 ,
则,又,所以 .
题组二 常错题
5.在中,若,则,的大小关系为_________;若,则 ,
的大小关系为_________.
[解析] 根据正弦定理知,在中, ,
.
6.在中,内角,,的对边分别为,,,已知 , ,
,则 ______________.
或
[解析] 由正弦定理得,
因为, ,所以 或 .
7.在中,内角,,所对的边分别为,,,若,, ,则
_ ____, ___.
1
[解析] .
由余弦定理得,所以 .
探究点一 利用余弦定理、正弦定理解基本量问题
例1 在中,内角,,所对的边分别为,, ,且
,, .
(1) 求 的面积;
解:因为在中,, ,
所以 ,
故的面积为 .
[思路点拨]先算出 ,然后直接由三角形的面积公式求解即可;
(2) 求及 的值.
解: 在中,,, ,
所以由余弦定理得 ,
又,所以.
由(1)可知,所以由正弦定理得 ,
即,解得 .
[思路点拨]先由余弦定理求出,然后由正弦定理求解 即可.
变式题1(1) [2023·全国乙卷] 在中,内角,,的对边分别是, ,
,若,且,则 ( )
C
A. B. C. D.
[解析] 方法一:因为 ,
所以由正弦定理得,即,
所以 或 (舍).
因为, ,所以.所以 .故选C.
方法二:由余弦定理得,整理得 ,
所以为直角三角形,且,又,所以 .故选C.
(2) [2023·北京卷] 在中, ,
则 ( )
B
A. B. C. D.
[解析] 因为 ,
所以由正弦定理得,即,
则 ,故,
又 ,所以 .故选B.
(3) 记的内角,,的对边分别为,,,面积为 ,
,,则 ______.
[解析] , ,
根据余弦定理得, .
变式题2 [2023·天津卷] 在中,角,,所对的边分别是,, .已知
,, .
(1) 求 的值;
解:因为 ,所以,都为锐角,且 .
由正弦定理得,所以,解得 .
(2) 求 的值;
解: 由余弦定理得,所以 ,
整理得,解得或(舍),所以 .
(3) 求 .
解: 方法一:因为,为锐角,所以 ,
所以
.
方法二:因为,为锐角,所以.
由正弦定理得 ,所以,解得,
又为锐角,所以 ,
所以 .
探究点二 利用余弦定理、正弦定理判定三角形的形状
例2(1) 在中,若,则 是( )
B
A.等腰三角形 B.直角三角形
C.等腰或直角三角形 D.钝角三角形
[解析] , ,
,, ,, .故选B.
[思路点拨]根据正弦定理可得,整理可得 ,
又由,可得 ,即可得解.
(2) 在中,已知,且 ,则该三角
形的形状是( )
C
A.直角三角形 B.等腰三角形 C.等边三角形 D.钝角三角形
[解析] ,,又, .
由,得,,即 ,
又, 该三角形为等边三角形.
[思路点拨]首先利用余弦定理求出角 ,再利用正弦定理与余弦定理将
化简得到, 的关系,进而判断出三角形形状.
变式题(1) (多选题)已知的内角,,所对的边分别为,, ,
则下列说法中正确的有( )
ACD
A.若,则 一定是等边三角形
B.若,则 一定是等腰三角形
C.若,则 一定是等腰三角形
D.若,则 一定是钝角三角形
[解析] 对于A,若,则由正弦定理得 ,
即,则,所以 一定是等边三角形,故A正确;
对于B,若,则由正弦定理得 ,
即,则或 ,即或 ,
所以是等腰三角形或直角三角形,故B错误;
对于C,若 ,则由正弦定理得,
所以 ,即,所以一定是等腰三角形,故C正确;
对于D,在 中,因为,且,
所以,所以角 为钝角,所以一定是钝角三角形,故D正确.故选 .
(2) 在中,内角,,所对的边分别是,, ,若
,则 的形状为( )
D
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
[解析] 因为 ,
所以由正弦定理得,
又 ,
所以 ,
所以,所以或,
所以或 ,所以 为等腰三角形或直角三角形.
探究点三 正余弦定理在几何中的应用
微点1 最值、范围问题
例3 在锐角三角形中,内角,,的对边分别为,, ,从①
,② 这两个条件中选择一个作为已知条
件.
(1) 求角 的大小;
[思路点拨]选条件①,由已知等式得,根据正切函数值得角 的大小;
选条件②,由已知等式结合正弦定理与三角恒等变换,化简得 ,进而可
得角 的大小.
解:选条件①:因为,所以 ,
所以,又因为,所以,所以 ,
所以 .
选条件②:因为 ,
所以由正弦定理可得 ,
即,
又因为 ,所以.因为,所以 .
(2) 若,求 的周长的取值范围.
[思路点拨]根据正弦定理,结合三角恒等变换将三角形的周长转化为正弦型三
角函数,利用正弦型三角函数的性质求 周长的取值范围即可.
解: 由正弦定理得,
则 ,,又 ,,所以,
又 为锐角三角形,所以,,则 ,
所以
,
因为,所以,则 ,
所以,即的周长的取值范围为
[总结反思]
破解此类问题的关键:一是观察已知三角恒等式,判断是边往角化还是角往边化,从
而利用正弦定理或余弦定理进行转化;二是把所求的取值范围或最值问题转化为三
角函数问题,利用三角函数的单调性进行求解,或利用基本不等式、三角函数的有
界性进行求解.
解:方法一:在中,因为为的中点,, ,
所以 ,
解得.
在中, ,
由余弦定理得,
即 ,可得,则 ,
,所以 .
方法二:在中,因为为的中点,, ,
所以 ,
解得 .
在中,由余弦定理得 ,
即,可得,则 ,
则,,过作于,
于是 ,,则,所以 .
(2) 若,求, .
解: 方法一:在与 中,
由余弦定理得整理得 ,
又,所以 ,
又,所以,
而 ,于是,所以 .
[思路点拨]思路一:利用余弦定理求出,再利用三角形的面积公式求出 ,
即可求解,;思路二:由已知利用向量相关计算建立关系求出 ,再利用三角形
的面积公式求出,即可求解, .
方法二:在中,因为为的中点,所以 ,
又 ,
所以,
即 ,可得,
又,
所以 ,而 ,于是,
所以 .
1.【微点1、微点2】在中,内角,,的对边分别为,, ,已知
,若内角的平分线(在 边上)
的长为2,则 的最小值为( )
D
A.10 B.12 C.16 D.18
[解析] , ,
即,则,又 ,.
平分内角,.
由 ,得,
即,即 ,
,
当且仅当时等号成立,即 的最小值为18.故选D.
2.【微点2】[2023·安徽蚌埠质检] 在中,为上一点,且 ,
,,则 ( )
D
A. B. C. D.
[解析] 方法一:在和中,有, ,
故.设,则,又,所以.
设 ,则由得,
又 ,所以由余弦定理可得,
整理得,则 ,
所以,故 .
方法二:设,则 .
在和中,有 ,
由正弦定理有 ,,
两式相除整理得 ,
则,所以 ,
即,解得或.
因为在 中,,所以,故 ,故选D.
3.【微点1】[2022·新高考全国Ⅰ卷] 记的内角,,的对边分别为,, ,
已知 .
(1) 若,求 ;
解:由已知条件得 ,
则
,
所以,所以 .
由题知,所以,所以 ,
所以,可得 .
(2) 求 的最小值.
解: 由(1)知,则 ,
则 .
由正弦定理得
,
当且仅当时等号成立,所以的最小值为 .
4.【微点2】[2023·福建泉州七中模拟] 如图所示,在四边形
中,,, ,从条件①,条件
②这两个条件中选择一个作为已知,解决下列问题.
(1) 求 的长;
解:选条件①:由余弦定理得 ,
解得 .
选条件②:在 中,
由余弦定理得,
在 中,由余弦定理得,
因为 ,所以,
即,可得 .
(2) 求四边形 的面积.
条件①: ;
条件②: .
解: 选条件①:, ,
故 .
在中,,所以 ,
故 ,所以四边形的面积为 .
选条件②:,则,故 .
因为 ,所以 ,
则 ,
,
故四边形 的面积为 .
提升习题
1 [配例1使用] 在; 这两
个条件中任选一个,补充在下面问题中,并加以解答.
已知的内角,,所对的边分别为,, ,________.
(1) 求 的值;
解:若选①,由得 ,
由正弦定理得,又,所以,
所以 ,又,,所以 .
若选②,由已知及正弦定理得 ,
所以 ,
所以 ,
所以,又,所以,所以 ,
又,,,所以 .
(2) 若的面积为2,,求 的周长.
注:若选择多个条件分别解答,则按第一个解答计分.
解: 由的面积为2,得,所以 ,
由(1)可得,
由余弦定理得 ,所以,
所以,
所以 的周长为 .
2 [配例2使用]的三个内角,,满足 ,且
,则这个三角形的形状是( )
B
A.直角三角形 B.等边三角形 C.等腰直角三角形 D.钝角三角形
[解析] 因为 ,,所以.
因为 ,所以由正弦定理得,
又由余弦定理得 ,所以,
整理得,所以,所以 是等边三角形.故选B.
例3 [配例3使用] [2023·山东枣庄三模] 已知的内角,, 的对边
分别为,,,且 .
(1) 求 ;
解:由余弦定理知 ,
则 ,
所以,所以 ,
则,又因为,所以 ,
整理得 ,又,所以 .
(2) 求 的最小值.
解: 由(1)知,所以 ,
所以,当且仅当时等号成立,
所以 的最小值为 .
4 [配例4使用] 如图,在平面四边形 中,
, ,
, .
(1) 求 ;
解:由 ,
根据正弦定理得 ,
,,即 ,
即 ,
又 , , ,即 .
(2) 若,求 的面积.
解: 设 , 四边形的内角和为 , .
在中,由正弦定理得,即 .
在中,,即,
又 ,,则,即,
即 .
, , , ,即 ,
则 ,
.
, .
高考数学一轮复习
余弦定理、正弦定理
◆ 知识聚焦 ◆
1. 正、余弦定理
在中,内角,,所对的边分别是,,,为 外接圆的半径,则
正弦定理 余弦定理
公 式 ;
;
正弦定理 余弦定理
常 见 变 形 , , ; #b# ,, ; #b# ; #b# , , #b# ;
;
续表
2. 在中,已知,和 时,解的情况
为锐角 为钝角或直角
图形
关系式
解的个数 一解 两解 一解 一解 无解
3. 面积公式
;
是的内切圆半径,是 的外接圆半
径,并可由此计算, .
常用结论
1.正弦定理的应用
①边化角,角化边 .
②大边对大角,大角对大边
.
③合分比:
是 的外接圆半径).
2.内角和定理: .
.
同理有:, .
.
③斜三角形中,
.
; .
⑤在中,内角,,成等差数列, .
◆ 对点演练 ◆
题组一 常识题
1. 在中,,,,则 _ ___.
[解析] 在中,设,, ,
则由余弦定理得,
因为为 的内角,所以 .
2. 已知的内角,,的对边分别为,,,若 的
面积为4,, ,则 ___.
8
[解析] 由,得 .
3. 在中,已知, , ,则边
_ _________.
[解析] ,
由正弦定理,得 ,得 .
4.[教材改编] 在中,内角,,的对边分别为,,,若 ,
且,则 ___.
[解析] 由余弦定理可得,化简整理得 ,
则,又,所以 .
题组二 常错题
5.在中,若,则,的大小关系为_________;若,则 ,
的大小关系为_________.
[解析] 根据正弦定理知,在中, ,
.
6.在中,内角,,的对边分别为,,,已知 , ,
,则 ______________.
或
[解析] 由正弦定理得,
因为, ,所以 或 .
7.在中,内角,,所对的边分别为,,,若,, ,则
_ ____, ___.
1
[解析] .
由余弦定理得,所以 .
探究点一 利用余弦定理、正弦定理解基本量问题
例1 在中,内角,,所对的边分别为,, ,且
,, .
(1) 求 的面积;
解:因为在中,, ,
所以 ,
故的面积为 .
[思路点拨]先算出 ,然后直接由三角形的面积公式求解即可;
(2) 求及 的值.
解: 在中,,, ,
所以由余弦定理得 ,
又,所以.
由(1)可知,所以由正弦定理得 ,
即,解得 .
[思路点拨]先由余弦定理求出,然后由正弦定理求解 即可.
变式题1(1) [2023·全国乙卷] 在中,内角,,的对边分别是, ,
,若,且,则 ( )
C
A. B. C. D.
[解析] 方法一:因为 ,
所以由正弦定理得,即,
所以 或 (舍).
因为, ,所以.所以 .故选C.
方法二:由余弦定理得,整理得 ,
所以为直角三角形,且,又,所以 .故选C.
(2) [2023·北京卷] 在中, ,
则 ( )
B
A. B. C. D.
[解析] 因为 ,
所以由正弦定理得,即,
则 ,故,
又 ,所以 .故选B.
(3) 记的内角,,的对边分别为,,,面积为 ,
,,则 ______.
[解析] , ,
根据余弦定理得, .
变式题2 [2023·天津卷] 在中,角,,所对的边分别是,, .已知
,, .
(1) 求 的值;
解:因为 ,所以,都为锐角,且 .
由正弦定理得,所以,解得 .
(2) 求 的值;
解: 由余弦定理得,所以 ,
整理得,解得或(舍),所以 .
(3) 求 .
解: 方法一:因为,为锐角,所以 ,
所以
.
方法二:因为,为锐角,所以.
由正弦定理得 ,所以,解得,
又为锐角,所以 ,
所以 .
探究点二 利用余弦定理、正弦定理判定三角形的形状
例2(1) 在中,若,则 是( )
B
A.等腰三角形 B.直角三角形
C.等腰或直角三角形 D.钝角三角形
[解析] , ,
,, ,, .故选B.
[思路点拨]根据正弦定理可得,整理可得 ,
又由,可得 ,即可得解.
(2) 在中,已知,且 ,则该三角
形的形状是( )
C
A.直角三角形 B.等腰三角形 C.等边三角形 D.钝角三角形
[解析] ,,又, .
由,得,,即 ,
又, 该三角形为等边三角形.
[思路点拨]首先利用余弦定理求出角 ,再利用正弦定理与余弦定理将
化简得到, 的关系,进而判断出三角形形状.
变式题(1) (多选题)已知的内角,,所对的边分别为,, ,
则下列说法中正确的有( )
ACD
A.若,则 一定是等边三角形
B.若,则 一定是等腰三角形
C.若,则 一定是等腰三角形
D.若,则 一定是钝角三角形
[解析] 对于A,若,则由正弦定理得 ,
即,则,所以 一定是等边三角形,故A正确;
对于B,若,则由正弦定理得 ,
即,则或 ,即或 ,
所以是等腰三角形或直角三角形,故B错误;
对于C,若 ,则由正弦定理得,
所以 ,即,所以一定是等腰三角形,故C正确;
对于D,在 中,因为,且,
所以,所以角 为钝角,所以一定是钝角三角形,故D正确.故选 .
(2) 在中,内角,,所对的边分别是,, ,若
,则 的形状为( )
D
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
[解析] 因为 ,
所以由正弦定理得,
又 ,
所以 ,
所以,所以或,
所以或 ,所以 为等腰三角形或直角三角形.
探究点三 正余弦定理在几何中的应用
微点1 最值、范围问题
例3 在锐角三角形中,内角,,的对边分别为,, ,从①
,② 这两个条件中选择一个作为已知条
件.
(1) 求角 的大小;
[思路点拨]选条件①,由已知等式得,根据正切函数值得角 的大小;
选条件②,由已知等式结合正弦定理与三角恒等变换,化简得 ,进而可
得角 的大小.
解:选条件①:因为,所以 ,
所以,又因为,所以,所以 ,
所以 .
选条件②:因为 ,
所以由正弦定理可得 ,
即,
又因为 ,所以.因为,所以 .
(2) 若,求 的周长的取值范围.
[思路点拨]根据正弦定理,结合三角恒等变换将三角形的周长转化为正弦型三
角函数,利用正弦型三角函数的性质求 周长的取值范围即可.
解: 由正弦定理得,
则 ,,又 ,,所以,
又 为锐角三角形,所以,,则 ,
所以
,
因为,所以,则 ,
所以,即的周长的取值范围为
[总结反思]
破解此类问题的关键:一是观察已知三角恒等式,判断是边往角化还是角往边化,从
而利用正弦定理或余弦定理进行转化;二是把所求的取值范围或最值问题转化为三
角函数问题,利用三角函数的单调性进行求解,或利用基本不等式、三角函数的有
界性进行求解.
解:方法一:在中,因为为的中点,, ,
所以 ,
解得.
在中, ,
由余弦定理得,
即 ,可得,则 ,
,所以 .
方法二:在中,因为为的中点,, ,
所以 ,
解得 .
在中,由余弦定理得 ,
即,可得,则 ,
则,,过作于,
于是 ,,则,所以 .
(2) 若,求, .
解: 方法一:在与 中,
由余弦定理得整理得 ,
又,所以 ,
又,所以,
而 ,于是,所以 .
[思路点拨]思路一:利用余弦定理求出,再利用三角形的面积公式求出 ,
即可求解,;思路二:由已知利用向量相关计算建立关系求出 ,再利用三角形
的面积公式求出,即可求解, .
方法二:在中,因为为的中点,所以 ,
又 ,
所以,
即 ,可得,
又,
所以 ,而 ,于是,
所以 .
1.【微点1、微点2】在中,内角,,的对边分别为,, ,已知
,若内角的平分线(在 边上)
的长为2,则 的最小值为( )
D
A.10 B.12 C.16 D.18
[解析] , ,
即,则,又 ,.
平分内角,.
由 ,得,
即,即 ,
,
当且仅当时等号成立,即 的最小值为18.故选D.
2.【微点2】[2023·安徽蚌埠质检] 在中,为上一点,且 ,
,,则 ( )
D
A. B. C. D.
[解析] 方法一:在和中,有, ,
故.设,则,又,所以.
设 ,则由得,
又 ,所以由余弦定理可得,
整理得,则 ,
所以,故 .
方法二:设,则 .
在和中,有 ,
由正弦定理有 ,,
两式相除整理得 ,
则,所以 ,
即,解得或.
因为在 中,,所以,故 ,故选D.
3.【微点1】[2022·新高考全国Ⅰ卷] 记的内角,,的对边分别为,, ,
已知 .
(1) 若,求 ;
解:由已知条件得 ,
则
,
所以,所以 .
由题知,所以,所以 ,
所以,可得 .
(2) 求 的最小值.
解: 由(1)知,则 ,
则 .
由正弦定理得
,
当且仅当时等号成立,所以的最小值为 .
4.【微点2】[2023·福建泉州七中模拟] 如图所示,在四边形
中,,, ,从条件①,条件
②这两个条件中选择一个作为已知,解决下列问题.
(1) 求 的长;
解:选条件①:由余弦定理得 ,
解得 .
选条件②:在 中,
由余弦定理得,
在 中,由余弦定理得,
因为 ,所以,
即,可得 .
(2) 求四边形 的面积.
条件①: ;
条件②: .
解: 选条件①:, ,
故 .
在中,,所以 ,
故 ,所以四边形的面积为 .
选条件②:,则,故 .
因为 ,所以 ,
则 ,
,
故四边形 的面积为 .
提升习题
1 [配例1使用] 在; 这两
个条件中任选一个,补充在下面问题中,并加以解答.
已知的内角,,所对的边分别为,, ,________.
(1) 求 的值;
解:若选①,由得 ,
由正弦定理得,又,所以,
所以 ,又,,所以 .
若选②,由已知及正弦定理得 ,
所以 ,
所以 ,
所以,又,所以,所以 ,
又,,,所以 .
(2) 若的面积为2,,求 的周长.
注:若选择多个条件分别解答,则按第一个解答计分.
解: 由的面积为2,得,所以 ,
由(1)可得,
由余弦定理得 ,所以,
所以,
所以 的周长为 .
2 [配例2使用]的三个内角,,满足 ,且
,则这个三角形的形状是( )
B
A.直角三角形 B.等边三角形 C.等腰直角三角形 D.钝角三角形
[解析] 因为 ,,所以.
因为 ,所以由正弦定理得,
又由余弦定理得 ,所以,
整理得,所以,所以 是等边三角形.故选B.
例3 [配例3使用] [2023·山东枣庄三模] 已知的内角,, 的对边
分别为,,,且 .
(1) 求 ;
解:由余弦定理知 ,
则 ,
所以,所以 ,
则,又因为,所以 ,
整理得 ,又,所以 .
(2) 求 的最小值.
解: 由(1)知,所以 ,
所以,当且仅当时等号成立,
所以 的最小值为 .
4 [配例4使用] 如图,在平面四边形 中,
, ,
, .
(1) 求 ;
解:由 ,
根据正弦定理得 ,
,,即 ,
即 ,
又 , , ,即 .
(2) 若,求 的面积.
解: 设 , 四边形的内角和为 , .
在中,由正弦定理得,即 .
在中,,即,
又 ,,则,即,
即 .
, , , ,即 ,
则 ,
.
, .
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
