3.6角(第1课时角)课件(共32张PPT)-七年级数学上册考试满分全攻略同步备课备考系列(华师大版2024)
文档属性
| 名称 | 3.6角(第1课时角)课件(共32张PPT)-七年级数学上册考试满分全攻略同步备课备考系列(华师大版2024) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-25 07:47:12 | ||
图片预览









文档简介
(共32张PPT)
华师大版(2024)七年级数学上册 第三章 图形的初步认识
3.6 角
第一课时 角
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1. 会正确使用量角器,认识角的常用度量单位,并会进行度、分、秒的简单换算.
2. 通过在图片、实例中找角,培养学生的观察力,能把实际问题转化为数学问题,培养学生对数学的好奇心与求知欲.
重点:理解角的概念,掌握角的表示方法及方位角.
难点:角的表示方法及度、分、秒之间的换算.
情景导入
观察图中的图形,你发现它们有什么共同的特点吗?
这些图形都给出了角的形象.
新知探究
在小学里,我们已学习过角的概念,角是由两条有公共端点的射线组成的图形.
如下图,角更可以看成是由一条射线绕着它的端点旋转而成的图形. 射线的端点叫做角的顶点,起始位置的射线叫做角的始边,终止位置的射线叫做角的终边.
新知探究
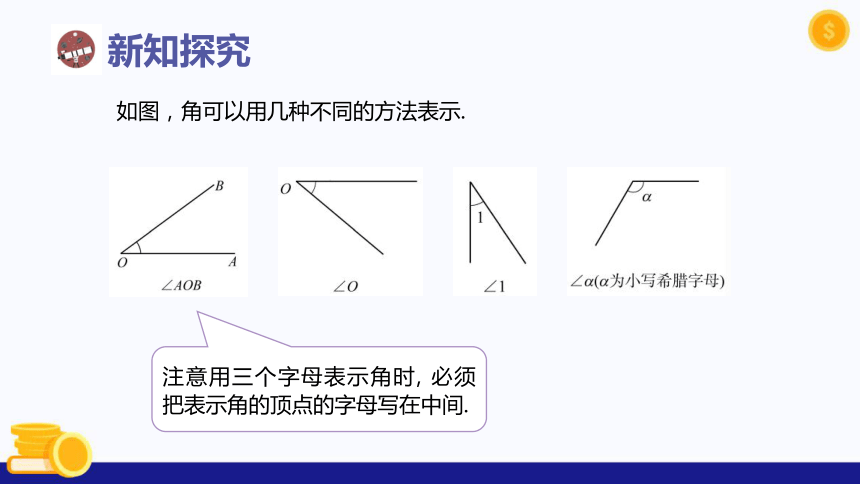
如图,角可以用几种不同的方法表示.
注意用三个字母表示角时, 必须 把表示角的顶点的字母写在中间.
新知探究
在下图中可以观察到两种特殊情况: 第一种情况是绕着射线的端点旋转到角的终边和始边成一条直线,这时所成的角叫做平角;第二种情况是绕着射线的端点旋转到终边和始边再次重合,这时所成的角叫做周角.
A
O
B
A
O
(B)
本册教科书中的角,除了周角和平角外,一般是指小于平角的角.
新知探究
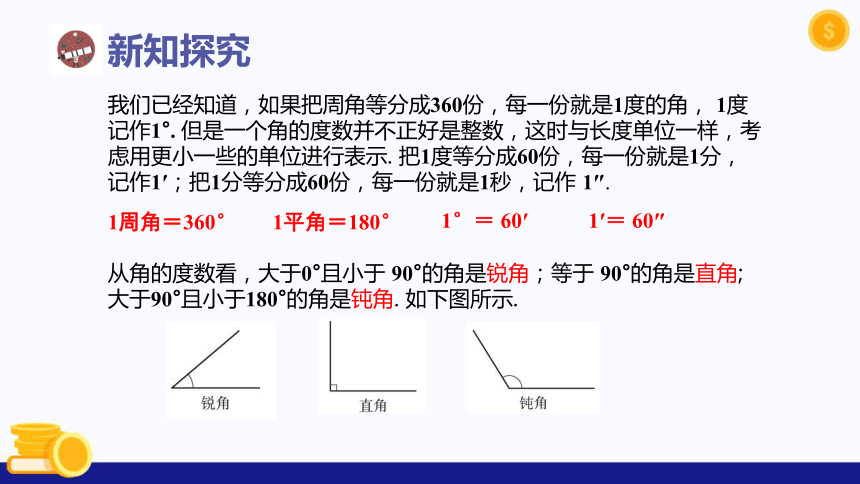
我们已经知道,如果把周角等分成360份,每一份就是1度的角, 1度记作1°. 但是一个角的度数并不正好是整数,这时与长度单位一样,考虑用更小一些的单位进行表示. 把1度等分成60份,每一份就是1分,记作1′;把1分等分成60份,每一份就是1秒,记作 1″.
1周角=360°
1平角=180°
1°= 60′
1′= 60″
从角的度数看,大于0°且小于 90°的角是锐角;等于 90°的角是直角; 大于90°且小于180°的角是钝角. 如下图所示.
课本例题
例1(1)把18°15′化成用度表示的角;
(2)把93.2°化成用度、分、秒表示的角.
解:(1)先把15′化成度,即
所以 18°15′=18.25′
(2)因为1°=60′,
所以 0.2°=60′×0.2=12′
因此 93.2°=93°12′
北
南
西
东
东北
西北
西南
东南
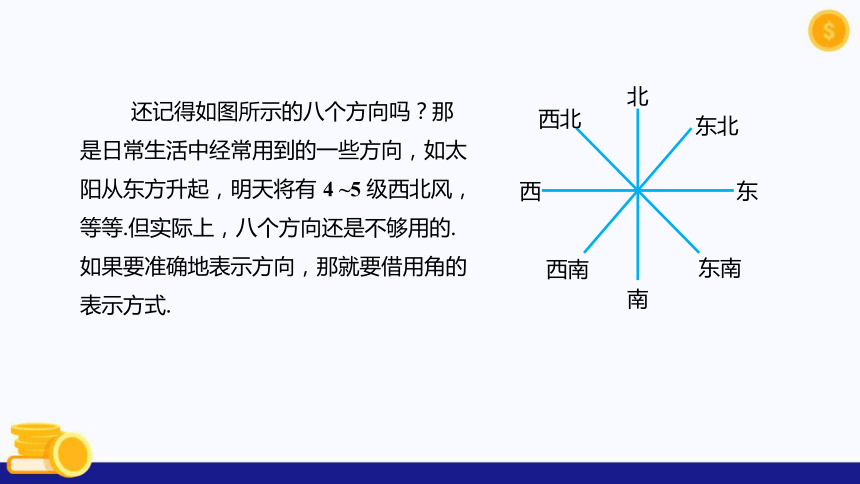
还记得如图所示的八个方向吗?那是日常生活中经常用到的一些方向,如太阳从东方升起,明天将有 4 ~5 级西北风,等等.但实际上,八个方向还是不够用的. 如果要准确地表示方向,那就要借用角的表示方式.
课本例题
北
东
西
南
A
30°
60°
O
25°
解:如图所示
例2 如图,OA是表示北偏东30°方向的一条射线.
仿照这条射线,画出表示下列方向的射线:
(1)南偏东25°;
(2)北偏西60°.
以正南方向的射线为始边, 逆时针旋转25°, 所成的角的终边即为所求的射线.
(2) 以正北方向的射线为始边, 逆时针旋转60°,
所成的角的终边即为所求的射线.
读一读
我们还可以以正北、正南方向为基准,描述物体运动的方向. 如:“北偏东30°”“南偏东 25°”“北偏西 60°”.
轮船、飞机等物体运动的方向与正北方向之间的夹角,即以测量点的正北方向为起始边,依顺时针方向到目标方向线之间的水平夹角称为方位角,领航员常用地图和罗盘进行方位角的测定.
课堂练习
1. 根据图示填空:
(1)正东和正西方向所成的角______度;
(2)正南和西南方向所成的角______度;
(3)东北和西北方向所成的角______度;
(4)正西和东南方向所成的角______度.
180
45
90
135
2. 用直尺画出30°、45°、60°、120°的角.随后用量角器量一量,比一比谁画的角最为准确.
分层练习-基础
知识点1 角及有关角的定义
1. 下列说法中,正确的是( B )
A. 两条射线所组成的图形叫做角
B. 角的大小与所画的角的两边的长短无关
C. 角的两边是两条线段
D. 角的两边是两条直线
【点拨】
角是由同一个点发出的两条射线组成的, 角的大小
与所画角的两边的长短无关, 所以B正确.
B
2. 已知, O 为直线 AB 上的一点,画出射线 OC (如图①),则
图中有 个角(除平角外);再画出射线 OD (如图②),
则图中有 个角(除平角外);再画出射线 OE (如图
③),则图中有 个角(除平角外).
2
5
9
知识点2 角的表示方法
3. [2024·河南商丘期末]如图,下列各个图形中,能用∠1,
∠ AOB ,∠ O 三种方法表示同一角的图形是( B )
B
4. 下列对于图形的描述中,正确的有( B )
A. 1个 B. 2个
C. 3个 D. 4个
B
知识点3 角的度量
5. [2023·临沂]如图中用量角器测得∠ ABC 的度数是( C )
A. 50° B. 80°
C. 130° D. 150°
C
6. 下面等式中,角度互化成立的是( D )
A. 83.5°=83°5'
C. 24°24'24″=24.44°
对于C,24″=0.4',24.4'≈0.41°,所以
24°24'24″≈24.41°,错误;
对于D,0.25°=15',所以41.25°=41°15',正确.
【点拨】
对于A,0.5°=30',所以83.5°=83°30',错误;
对于B,36″=0.6',12.6'=0.21°,所以37°12'36″
=37.21°,错误;
【答案】D
B. 37°12'36″=37.48°
D. 41.25°=41°15'
7. 计算:109°28'-70°31'= .
38°57'
知识点4 方向角与钟面角
8. [立德树人·爱国主义 2023 河北]淇淇一家要到革命圣地西
柏坡参观.如图,西柏坡位于淇淇家南偏西70°的方向,
则淇淇家位于西柏坡的( D )
D
A. 南偏西70°方向
B. 南偏东20°方向
C. 北偏西20°方向
D. 北偏东70°方向
9. [新考法 分类讨论法]当分针指向12,时针这时恰好与分针
成120°的角,此时是( D )
A. 9点钟 B. 8点钟
C. 4点钟 D. 8点钟或4点钟
【点拨】
当分针指向12,与时针的夹角为120°时,有如图两
种情况,此时是8点钟或4点钟,故选D.
D
10. 某一时刻,时钟上显示的时间是9点30分,则此时时针与
分针的夹角是( C )
A. 75° B. 90°
C. 105° D. 120°
【点拨】
当时间是9点30分时,时钟如图所示,此时时针与分
针的夹角为90°+15°=105°,故选C.
C
易错点 度、分、秒转化时,误按十进制进行换算
11. (1)把26.19°转化为用度、分、秒表示
为 ;
(2)把33°14'24″转化为用度表示为 .
26°11'24″
33.24°
分层练习-巩固
利用角的定义及度量画符合条件的角
12. 根据下列语句画图:
(1)画∠ AOB =100°;
(2)在∠ AOB 的内部画射线 OC ,使∠ BOC =50°;
(3)在∠ AOB 的外部画射线 OD ,使∠ DOA =40°;
(4)在射线 OD 上取点 E ,在射线 OA 上取点 F ,使
∠ OEF =90°.
【解】如图所示.
利用角度解决实际问题
13. [2024·长沙明德中学模拟]魏老师去市场买菜,他发现把5kg的菜放到秤上,指针盘上的指针转了180°.
(1)如果把0.5 kg的菜放到秤上,求指针转过的角度.
【解】 ×0.5=18°.
所以把0.5 kg的菜放到秤上,指针转过的角度是18°.
(2)如果指针转了270°,那么这些菜有多少千克?
【解】270°÷ =7.5(kg).
答:这些菜有7.5 kg.
分层练习-拓展
利用钟面上角的特征探求时针与分针夹角的度数
14. [新视角·项目探究题]综合与实践:
【问题提出】随着时间的变化,钟面上时针和分针形成
夹角的度数也随之变化,记旋转中心为点 O ,时针和分
针的夹角为∠α(∠α大于或等于0°,且小于或等于
180°).我们可以求出任意时刻∠α的度数吗?
【初步探究】小明所在的兴趣小组开展研究如下.
分针运动规律 分针每分钟走6°
时针运动规律 时针每小时走30°,即每分钟走0.5°
规定 当时针和分针指向刻度12时记为0°
特例探究1 (8时50分) 分针绕点 O 旋转所得角的度数是6°×50
=300°,时针绕点 O 旋转所得角的度数
是30°×8+0.5°×50=265°,所以
∠α=300°-265°=35°
特例探究2 (8时30分) 分针绕点 O 旋转所得角的度数是6°×30
=180°,时针绕点 O 旋转所得角的度数
是30°×8+0.5°×30=255°,所以
∠α=255°-180°=75°
特例探究3 (8时10分) 分针绕点 O 旋转所得角的度数是6°×10
=60°,时针绕点 O 旋转所得角的度数
是30°×8+0.5°×10=245°,此时
245°-60°=185°.因为185°>
180°,所以∠α=360°-185°=175°
【深入探究】
(1)当时间为7时30分时,∠α的度数为 ;
【点拨】
分针绕点 O 旋转所得角的度数是6°×30=180°,
时针绕点 O 旋转所得角的度数是30°×7+0.5°×30=225°,
所以∠α=225°-180°=45°.
45°
(2)王老师7时整从家中出门散步,当她返回家中时还不到8时,此时她发现时针与分针形成的夹角正好是直角,求王老师外出散步用了多少分钟?
【解】设王老师外出散步用了 x 分钟,
则 =90,
解得 x = 或 .
所以王老师外出散步用了 或 分钟.
课堂小结
角
定义
静态
动态
表示方法
角度换算——度的形式
度、分、秒的形式
应用
华师大版(2024)七年级数学上册 第三章 图形的初步认识
3.6 角
第一课时 角
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1. 会正确使用量角器,认识角的常用度量单位,并会进行度、分、秒的简单换算.
2. 通过在图片、实例中找角,培养学生的观察力,能把实际问题转化为数学问题,培养学生对数学的好奇心与求知欲.
重点:理解角的概念,掌握角的表示方法及方位角.
难点:角的表示方法及度、分、秒之间的换算.
情景导入
观察图中的图形,你发现它们有什么共同的特点吗?
这些图形都给出了角的形象.
新知探究
在小学里,我们已学习过角的概念,角是由两条有公共端点的射线组成的图形.
如下图,角更可以看成是由一条射线绕着它的端点旋转而成的图形. 射线的端点叫做角的顶点,起始位置的射线叫做角的始边,终止位置的射线叫做角的终边.
新知探究
如图,角可以用几种不同的方法表示.
注意用三个字母表示角时, 必须 把表示角的顶点的字母写在中间.
新知探究
在下图中可以观察到两种特殊情况: 第一种情况是绕着射线的端点旋转到角的终边和始边成一条直线,这时所成的角叫做平角;第二种情况是绕着射线的端点旋转到终边和始边再次重合,这时所成的角叫做周角.
A
O
B
A
O
(B)
本册教科书中的角,除了周角和平角外,一般是指小于平角的角.
新知探究
我们已经知道,如果把周角等分成360份,每一份就是1度的角, 1度记作1°. 但是一个角的度数并不正好是整数,这时与长度单位一样,考虑用更小一些的单位进行表示. 把1度等分成60份,每一份就是1分,记作1′;把1分等分成60份,每一份就是1秒,记作 1″.
1周角=360°
1平角=180°
1°= 60′
1′= 60″
从角的度数看,大于0°且小于 90°的角是锐角;等于 90°的角是直角; 大于90°且小于180°的角是钝角. 如下图所示.
课本例题
例1(1)把18°15′化成用度表示的角;
(2)把93.2°化成用度、分、秒表示的角.
解:(1)先把15′化成度,即
所以 18°15′=18.25′
(2)因为1°=60′,
所以 0.2°=60′×0.2=12′
因此 93.2°=93°12′
北
南
西
东
东北
西北
西南
东南
还记得如图所示的八个方向吗?那是日常生活中经常用到的一些方向,如太阳从东方升起,明天将有 4 ~5 级西北风,等等.但实际上,八个方向还是不够用的. 如果要准确地表示方向,那就要借用角的表示方式.
课本例题
北
东
西
南
A
30°
60°
O
25°
解:如图所示
例2 如图,OA是表示北偏东30°方向的一条射线.
仿照这条射线,画出表示下列方向的射线:
(1)南偏东25°;
(2)北偏西60°.
以正南方向的射线为始边, 逆时针旋转25°, 所成的角的终边即为所求的射线.
(2) 以正北方向的射线为始边, 逆时针旋转60°,
所成的角的终边即为所求的射线.
读一读
我们还可以以正北、正南方向为基准,描述物体运动的方向. 如:“北偏东30°”“南偏东 25°”“北偏西 60°”.
轮船、飞机等物体运动的方向与正北方向之间的夹角,即以测量点的正北方向为起始边,依顺时针方向到目标方向线之间的水平夹角称为方位角,领航员常用地图和罗盘进行方位角的测定.
课堂练习
1. 根据图示填空:
(1)正东和正西方向所成的角______度;
(2)正南和西南方向所成的角______度;
(3)东北和西北方向所成的角______度;
(4)正西和东南方向所成的角______度.
180
45
90
135
2. 用直尺画出30°、45°、60°、120°的角.随后用量角器量一量,比一比谁画的角最为准确.
分层练习-基础
知识点1 角及有关角的定义
1. 下列说法中,正确的是( B )
A. 两条射线所组成的图形叫做角
B. 角的大小与所画的角的两边的长短无关
C. 角的两边是两条线段
D. 角的两边是两条直线
【点拨】
角是由同一个点发出的两条射线组成的, 角的大小
与所画角的两边的长短无关, 所以B正确.
B
2. 已知, O 为直线 AB 上的一点,画出射线 OC (如图①),则
图中有 个角(除平角外);再画出射线 OD (如图②),
则图中有 个角(除平角外);再画出射线 OE (如图
③),则图中有 个角(除平角外).
2
5
9
知识点2 角的表示方法
3. [2024·河南商丘期末]如图,下列各个图形中,能用∠1,
∠ AOB ,∠ O 三种方法表示同一角的图形是( B )
B
4. 下列对于图形的描述中,正确的有( B )
A. 1个 B. 2个
C. 3个 D. 4个
B
知识点3 角的度量
5. [2023·临沂]如图中用量角器测得∠ ABC 的度数是( C )
A. 50° B. 80°
C. 130° D. 150°
C
6. 下面等式中,角度互化成立的是( D )
A. 83.5°=83°5'
C. 24°24'24″=24.44°
对于C,24″=0.4',24.4'≈0.41°,所以
24°24'24″≈24.41°,错误;
对于D,0.25°=15',所以41.25°=41°15',正确.
【点拨】
对于A,0.5°=30',所以83.5°=83°30',错误;
对于B,36″=0.6',12.6'=0.21°,所以37°12'36″
=37.21°,错误;
【答案】D
B. 37°12'36″=37.48°
D. 41.25°=41°15'
7. 计算:109°28'-70°31'= .
38°57'
知识点4 方向角与钟面角
8. [立德树人·爱国主义 2023 河北]淇淇一家要到革命圣地西
柏坡参观.如图,西柏坡位于淇淇家南偏西70°的方向,
则淇淇家位于西柏坡的( D )
D
A. 南偏西70°方向
B. 南偏东20°方向
C. 北偏西20°方向
D. 北偏东70°方向
9. [新考法 分类讨论法]当分针指向12,时针这时恰好与分针
成120°的角,此时是( D )
A. 9点钟 B. 8点钟
C. 4点钟 D. 8点钟或4点钟
【点拨】
当分针指向12,与时针的夹角为120°时,有如图两
种情况,此时是8点钟或4点钟,故选D.
D
10. 某一时刻,时钟上显示的时间是9点30分,则此时时针与
分针的夹角是( C )
A. 75° B. 90°
C. 105° D. 120°
【点拨】
当时间是9点30分时,时钟如图所示,此时时针与分
针的夹角为90°+15°=105°,故选C.
C
易错点 度、分、秒转化时,误按十进制进行换算
11. (1)把26.19°转化为用度、分、秒表示
为 ;
(2)把33°14'24″转化为用度表示为 .
26°11'24″
33.24°
分层练习-巩固
利用角的定义及度量画符合条件的角
12. 根据下列语句画图:
(1)画∠ AOB =100°;
(2)在∠ AOB 的内部画射线 OC ,使∠ BOC =50°;
(3)在∠ AOB 的外部画射线 OD ,使∠ DOA =40°;
(4)在射线 OD 上取点 E ,在射线 OA 上取点 F ,使
∠ OEF =90°.
【解】如图所示.
利用角度解决实际问题
13. [2024·长沙明德中学模拟]魏老师去市场买菜,他发现把5kg的菜放到秤上,指针盘上的指针转了180°.
(1)如果把0.5 kg的菜放到秤上,求指针转过的角度.
【解】 ×0.5=18°.
所以把0.5 kg的菜放到秤上,指针转过的角度是18°.
(2)如果指针转了270°,那么这些菜有多少千克?
【解】270°÷ =7.5(kg).
答:这些菜有7.5 kg.
分层练习-拓展
利用钟面上角的特征探求时针与分针夹角的度数
14. [新视角·项目探究题]综合与实践:
【问题提出】随着时间的变化,钟面上时针和分针形成
夹角的度数也随之变化,记旋转中心为点 O ,时针和分
针的夹角为∠α(∠α大于或等于0°,且小于或等于
180°).我们可以求出任意时刻∠α的度数吗?
【初步探究】小明所在的兴趣小组开展研究如下.
分针运动规律 分针每分钟走6°
时针运动规律 时针每小时走30°,即每分钟走0.5°
规定 当时针和分针指向刻度12时记为0°
特例探究1 (8时50分) 分针绕点 O 旋转所得角的度数是6°×50
=300°,时针绕点 O 旋转所得角的度数
是30°×8+0.5°×50=265°,所以
∠α=300°-265°=35°
特例探究2 (8时30分) 分针绕点 O 旋转所得角的度数是6°×30
=180°,时针绕点 O 旋转所得角的度数
是30°×8+0.5°×30=255°,所以
∠α=255°-180°=75°
特例探究3 (8时10分) 分针绕点 O 旋转所得角的度数是6°×10
=60°,时针绕点 O 旋转所得角的度数
是30°×8+0.5°×10=245°,此时
245°-60°=185°.因为185°>
180°,所以∠α=360°-185°=175°
【深入探究】
(1)当时间为7时30分时,∠α的度数为 ;
【点拨】
分针绕点 O 旋转所得角的度数是6°×30=180°,
时针绕点 O 旋转所得角的度数是30°×7+0.5°×30=225°,
所以∠α=225°-180°=45°.
45°
(2)王老师7时整从家中出门散步,当她返回家中时还不到8时,此时她发现时针与分针形成的夹角正好是直角,求王老师外出散步用了多少分钟?
【解】设王老师外出散步用了 x 分钟,
则 =90,
解得 x = 或 .
所以王老师外出散步用了 或 分钟.
课堂小结
角
定义
静态
动态
表示方法
角度换算——度的形式
度、分、秒的形式
应用
同课章节目录
