4.3用一元一次方程解决问题(第3课时比例与图形问题) 课件(共25张PPT)
文档属性
| 名称 | 4.3用一元一次方程解决问题(第3课时比例与图形问题) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 949.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-24 14:51:59 | ||
图片预览








文档简介
(共25张PPT)
苏科版(2024) 七年级数学上册 第四章 一元一次方程
4.3 用一元一次方程解决问题
第三课时 比例与图形问题
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
会利用公式或找规律列公式解决实际问题,通过结合实际问题,创造活跃有趣的情境,提高学习兴趣.
能够根据实际问题中的数量关系列方程解决问题,培养数学建模能力,分析问题、解决问题的能力.
通过经历列一元一次方程解决实际问题的过程,逐步建立方程思想.培养建模意识.
情景导入
一. 列方程解应用题的解题步骤:
二. 帮助理解题意的辅助手段:
画线段图
直观的反映动态变化的过程
1.审 2.找 3.设 4.列 5.解 6.验 7.答
新知探究
王爷爷打算买32米的篱笆来围成一个6米宽的长方形菜园,请问这个菜园的长是多少米?
分析:这个问题中的等量关系:长方形的周长=(长+宽)×2
解:设这个长方形的长是米.
根据题意,得 (+6)×2=32
解得, =10
答:这个长方形的长是10米.
课本例题
例4 已知三角形三个角的度数之比为2:3:5,判断这个三角形的形状。
分析:这个问题中的等量关系:
第一个角+第二个角+第三个角=180°
解:设三角形三个角的大小分别为2x,3x,5x
根据题意,得 2+3+5=180°
解得, =18°
所以, 2=36°,3=54°,5=90°
三角形的三个角的大小分别为:36°,54°,90°
答:这个三角形是直角三角形。
课本例题
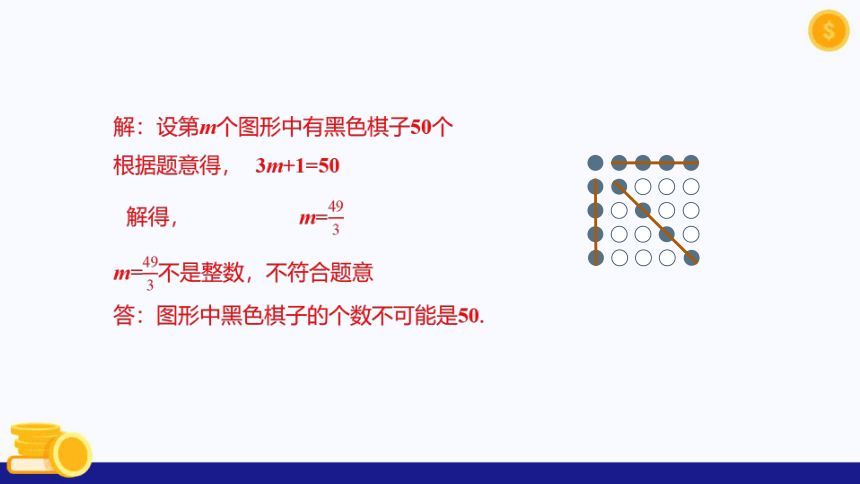
例5 用黑白两色棋子按如图所示方式摆图形,依此规律,图形中黑色棋子的个数有可能是50吗?
…
(1) (2) (3) (4)
解:设第m个图形中有黑色棋子50个
根据题意得, 3m+1=50
解得, m=
m=不是整数,不符合题意
答:图形中黑色棋子的个数不可能是50.
课堂练习
1. 已知一梯形的面积是120,上底是12,高是8,求下底的长.
解:设下底的长为x
(x+12)×8÷2=120
解得: x=18
答:下底的长为18.
2. 在明代数学著作《九章算法比类大全》中,有一个问题:“远望巍巍塔七层,红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”(倍加增指下一层灯的盏数比上一层增加1倍)请你解决这个问题。
解:设顶层有x盏灯
x+2x+4x+8x+16x+32x+64x=381
解得: x=3
答:顶层有3盏灯。
3.按如图所示的方式搭“小鱼”,若用了140根火柴棒,则“小鱼”有多少条?
分析:
1条小鱼8根火柴棒,2条小鱼8+6根火柴棒,
3条小鱼8+2×6根火柴棒
以此类推:
x条小鱼8+(x-1)×6根火柴棒
解:设“小鱼”有x条
根据题意,可得8+(x-1)×6=140
解得, x=23 答:有23条小鱼
分层练习-基础
1. [2024 无锡江阴市校级月考]甲、乙、丙三辆卡车运货的吨
数比是6∶7∶4.5,已知甲车比丙车多运货物12吨,则三
辆卡车共运货物( C )
A. 120吨 B. 130吨
C. 140吨 D. 150吨
C
2. 小明在日历的纵列上圈出了三个数,算出了它们的和,则和不可能是( A )
A. 15 B. 30
C. 45 D. 57
A
3. [2024 盐城东台市校级月考]三个连续奇数的和是75,则这
三个数中最小的数是 .
23
4. 三角形的三边之比是3∶5∶7,且最长边比最短边长8 cm,则该三角形的周长是 .
30 cm
5. [2024 扬州广陵区期末]如图是小明制作的一个半成品的平面图.
(1)在图中补充一个长方形 ABCD ,使该平面图能折叠成一个长方体盒子;
解:(1)如图所示.(答案不唯一)
(2)已知小明制作的长方体盒子的长是宽的2倍,宽是高的2倍,且长方体所有棱长的和为56 cm,求这个长方体盒子的表面积.
解:(2)设长方体盒子的高为 x cm,则宽为2 x cm,长为4 x cm,
根据题意,得4(4 x +2 x + x )=56,
解得 x =2.则长方体盒子的长为8 cm,宽为4 cm,高为2 cm.
所以长方体盒子的表面积为2×(4×8+4×2+8×2)=112(cm2).
6. [2024 南京六合区校级期末]某校的一间阶梯教室内,第1排的座位数为12,从第2排开始,每一排都比前一排增加 a 个座位.
(1)则第4排的座位数为 ,第 n 排的座位数为 ;
12+3 a
12+( n -1) a
(2)已知前5排座位数的和是第15排座位数的2倍,求 a
的值.
解:由题意,得12+12+ a +12+2 a +12+3 a +12+
4 a =2(12+14 a ),解得 a =2.
7. [2024 宿迁期中]如图是一组有规律的图案.
(1)第1个图案由4个基础图形组成,第2个图案由 个
基础图形组成,…,第 n 个图案由 个基础
图形组成(用含 n 的代数式表示).
7
(3 n +1)
(2)在上面的图案中,能否找到一个由2 023个基础图形组成的图案?如果能,说明是第几个图案;如果不能,说明理由.
解:能.由(1)得第 n 个图案由(3 n +1)个基础图形组成,
根据题意,得3 n +1=2 023,解得 n =674.
所以能找到一个由2 023个基础图形组成的图案,
第674个图案由2 023个基础图案组成.
分层练习-巩固
8. 如图,在某月的日历表中用框数器“ ”框出3,5,11,17,19五个数,它们的和为55,若将“ ”在图中换个位置框出五个数,若它们的和是110,则中间的数为( D )
A. 15 B. 16
C. 21 D. 22
D
9. [2024 无锡新吴区期末]如图,在长方形 ABCD 中,放入5个形状、大小相同的小长方形(空白部分),其中 AB =5 cm, BC =9 cm,请认真观察思考并解答下列问题:
(1)求小长方形的长和宽;
解:设小长方形的长为 x cm,
则由图易知宽为(5- x ) cm,
由题意得 x +3(5- x )=9,解得 x =3.5-3=2(cm).
所以小长方形的长为3 cm,宽为2 cm.
(2)阴影部分图形的总面积为 .
15 cm2
分层练习-拓展
10. 【新视角·游戏活动型】幻方是我国的一种传统游戏,要求将数安排在方格中,使每行、每列及对角线上的3个数的和都相等.例如,在图①所示的幻方中,每行、每列及对角线上的3个数之和均为15.
(1)如图②,请在两个空白方格中填上适当的数,以满足
幻方游戏的要求;
(2)如图③,请在三个空白方格中填上适当的数,以满足幻方游戏的要求;
(3)如图④,试求幻方中 m , n 的值.
解:由题意得13-12+ m =-7+28+ n ,
所以 n = m -20.
由题图④最下面一行与最右边一行的和相等,
可得-7+28+ n = m -2+ n ,
解得 m =23.
所以 n =3.
所以 m 的值是23, n 的值是3.
课堂小结
利用公式、规律解决问题
1.找出题目中的公式、规律
2.列等量关系解题
苏科版(2024) 七年级数学上册 第四章 一元一次方程
4.3 用一元一次方程解决问题
第三课时 比例与图形问题
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
会利用公式或找规律列公式解决实际问题,通过结合实际问题,创造活跃有趣的情境,提高学习兴趣.
能够根据实际问题中的数量关系列方程解决问题,培养数学建模能力,分析问题、解决问题的能力.
通过经历列一元一次方程解决实际问题的过程,逐步建立方程思想.培养建模意识.
情景导入
一. 列方程解应用题的解题步骤:
二. 帮助理解题意的辅助手段:
画线段图
直观的反映动态变化的过程
1.审 2.找 3.设 4.列 5.解 6.验 7.答
新知探究
王爷爷打算买32米的篱笆来围成一个6米宽的长方形菜园,请问这个菜园的长是多少米?
分析:这个问题中的等量关系:长方形的周长=(长+宽)×2
解:设这个长方形的长是米.
根据题意,得 (+6)×2=32
解得, =10
答:这个长方形的长是10米.
课本例题
例4 已知三角形三个角的度数之比为2:3:5,判断这个三角形的形状。
分析:这个问题中的等量关系:
第一个角+第二个角+第三个角=180°
解:设三角形三个角的大小分别为2x,3x,5x
根据题意,得 2+3+5=180°
解得, =18°
所以, 2=36°,3=54°,5=90°
三角形的三个角的大小分别为:36°,54°,90°
答:这个三角形是直角三角形。
课本例题
例5 用黑白两色棋子按如图所示方式摆图形,依此规律,图形中黑色棋子的个数有可能是50吗?
…
(1) (2) (3) (4)
解:设第m个图形中有黑色棋子50个
根据题意得, 3m+1=50
解得, m=
m=不是整数,不符合题意
答:图形中黑色棋子的个数不可能是50.
课堂练习
1. 已知一梯形的面积是120,上底是12,高是8,求下底的长.
解:设下底的长为x
(x+12)×8÷2=120
解得: x=18
答:下底的长为18.
2. 在明代数学著作《九章算法比类大全》中,有一个问题:“远望巍巍塔七层,红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”(倍加增指下一层灯的盏数比上一层增加1倍)请你解决这个问题。
解:设顶层有x盏灯
x+2x+4x+8x+16x+32x+64x=381
解得: x=3
答:顶层有3盏灯。
3.按如图所示的方式搭“小鱼”,若用了140根火柴棒,则“小鱼”有多少条?
分析:
1条小鱼8根火柴棒,2条小鱼8+6根火柴棒,
3条小鱼8+2×6根火柴棒
以此类推:
x条小鱼8+(x-1)×6根火柴棒
解:设“小鱼”有x条
根据题意,可得8+(x-1)×6=140
解得, x=23 答:有23条小鱼
分层练习-基础
1. [2024 无锡江阴市校级月考]甲、乙、丙三辆卡车运货的吨
数比是6∶7∶4.5,已知甲车比丙车多运货物12吨,则三
辆卡车共运货物( C )
A. 120吨 B. 130吨
C. 140吨 D. 150吨
C
2. 小明在日历的纵列上圈出了三个数,算出了它们的和,则和不可能是( A )
A. 15 B. 30
C. 45 D. 57
A
3. [2024 盐城东台市校级月考]三个连续奇数的和是75,则这
三个数中最小的数是 .
23
4. 三角形的三边之比是3∶5∶7,且最长边比最短边长8 cm,则该三角形的周长是 .
30 cm
5. [2024 扬州广陵区期末]如图是小明制作的一个半成品的平面图.
(1)在图中补充一个长方形 ABCD ,使该平面图能折叠成一个长方体盒子;
解:(1)如图所示.(答案不唯一)
(2)已知小明制作的长方体盒子的长是宽的2倍,宽是高的2倍,且长方体所有棱长的和为56 cm,求这个长方体盒子的表面积.
解:(2)设长方体盒子的高为 x cm,则宽为2 x cm,长为4 x cm,
根据题意,得4(4 x +2 x + x )=56,
解得 x =2.则长方体盒子的长为8 cm,宽为4 cm,高为2 cm.
所以长方体盒子的表面积为2×(4×8+4×2+8×2)=112(cm2).
6. [2024 南京六合区校级期末]某校的一间阶梯教室内,第1排的座位数为12,从第2排开始,每一排都比前一排增加 a 个座位.
(1)则第4排的座位数为 ,第 n 排的座位数为 ;
12+3 a
12+( n -1) a
(2)已知前5排座位数的和是第15排座位数的2倍,求 a
的值.
解:由题意,得12+12+ a +12+2 a +12+3 a +12+
4 a =2(12+14 a ),解得 a =2.
7. [2024 宿迁期中]如图是一组有规律的图案.
(1)第1个图案由4个基础图形组成,第2个图案由 个
基础图形组成,…,第 n 个图案由 个基础
图形组成(用含 n 的代数式表示).
7
(3 n +1)
(2)在上面的图案中,能否找到一个由2 023个基础图形组成的图案?如果能,说明是第几个图案;如果不能,说明理由.
解:能.由(1)得第 n 个图案由(3 n +1)个基础图形组成,
根据题意,得3 n +1=2 023,解得 n =674.
所以能找到一个由2 023个基础图形组成的图案,
第674个图案由2 023个基础图案组成.
分层练习-巩固
8. 如图,在某月的日历表中用框数器“ ”框出3,5,11,17,19五个数,它们的和为55,若将“ ”在图中换个位置框出五个数,若它们的和是110,则中间的数为( D )
A. 15 B. 16
C. 21 D. 22
D
9. [2024 无锡新吴区期末]如图,在长方形 ABCD 中,放入5个形状、大小相同的小长方形(空白部分),其中 AB =5 cm, BC =9 cm,请认真观察思考并解答下列问题:
(1)求小长方形的长和宽;
解:设小长方形的长为 x cm,
则由图易知宽为(5- x ) cm,
由题意得 x +3(5- x )=9,解得 x =3.5-3=2(cm).
所以小长方形的长为3 cm,宽为2 cm.
(2)阴影部分图形的总面积为 .
15 cm2
分层练习-拓展
10. 【新视角·游戏活动型】幻方是我国的一种传统游戏,要求将数安排在方格中,使每行、每列及对角线上的3个数的和都相等.例如,在图①所示的幻方中,每行、每列及对角线上的3个数之和均为15.
(1)如图②,请在两个空白方格中填上适当的数,以满足
幻方游戏的要求;
(2)如图③,请在三个空白方格中填上适当的数,以满足幻方游戏的要求;
(3)如图④,试求幻方中 m , n 的值.
解:由题意得13-12+ m =-7+28+ n ,
所以 n = m -20.
由题图④最下面一行与最右边一行的和相等,
可得-7+28+ n = m -2+ n ,
解得 m =23.
所以 n =3.
所以 m 的值是23, n 的值是3.
课堂小结
利用公式、规律解决问题
1.找出题目中的公式、规律
2.列等量关系解题
同课章节目录
