6.1.1直线、射线、线段——直线、射线、线段的概念 课件(共26张PPT)
文档属性
| 名称 | 6.1.1直线、射线、线段——直线、射线、线段的概念 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 36.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-25 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
第6章 平面图形的初步认识
6.1.1 直线、射线、线段——概念
汇报人:WPS
教学目标
01
理解线段、射线和直线的联系与区别
02
掌握两个基本事实,理解两点之间的距离的概念
直线、射线、线段的概念
知识精讲
小学里,我们已经初步认识了直线、射线与线段。在下面的图片中,哪些图形可以看作是直线、射线、线段
01
射线
线段
直线
课堂引入
知识精讲
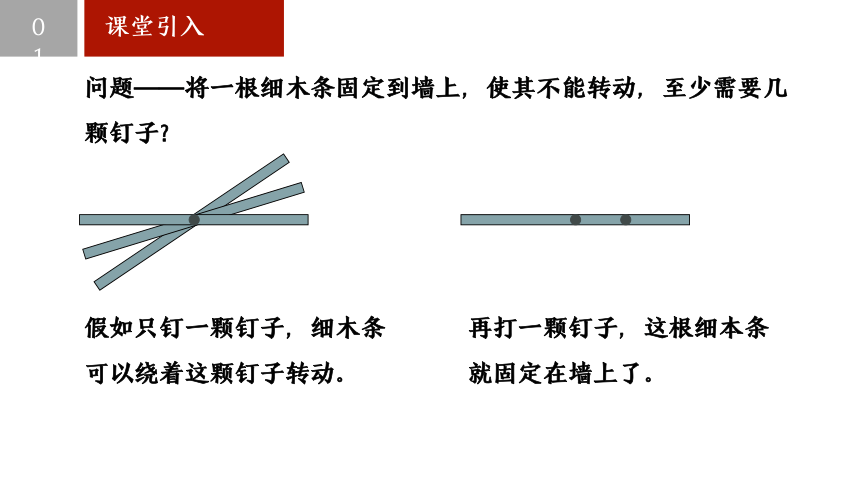
问题——将一根细木条固定到墙上,使其不能转动,至少需要几颗钉子
01
课堂引入
假如只钉一颗钉子,细木条可以绕着这颗钉子转动。
再打一颗钉子,这根细本条
就固定在墙上了。
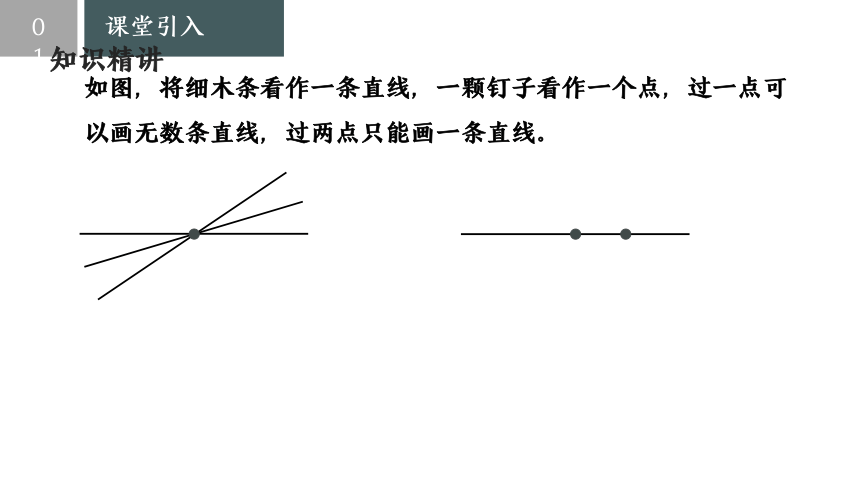
如图,将细木条看作一条直线,一颗钉子看作一个点,过一点可以画无数条直线,过两点只能画一条直线。
01
课堂引入
知识精讲
02
知识精讲
基本事实1
通过实践,人们总结出如下基本事实:
两点确定一条直线。
如图1,我们可以用直线上的两点来表示这条直线,记作直线AB或直线BA,也可以记作直线l。
02
知识精讲
如图2(1),直线上的一点将直线分成两条射线;
B
A
l
图1
图2(1)
如图2(2),由直线上的两点可以得到一条线段。
图2(2)
直线
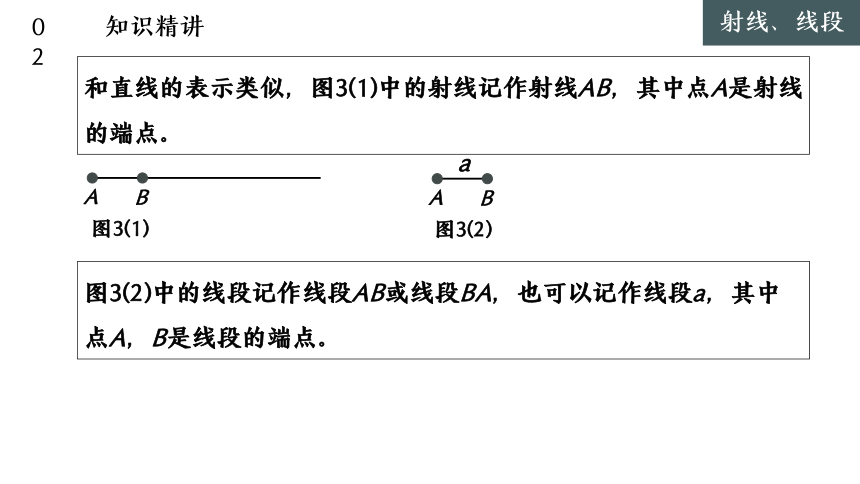
和直线的表示类似,图3(1)中的射线记作射线AB,其中点A是射线的端点。
02
知识精讲
图3(2)中的线段记作线段AB或线段BA,也可以记作线段a,其中点A,B是线段的端点。
B
A
图3(1)
B
A
图3(2)
a
射线、线段
讨论——1.如何由一条线段得到一条射线
①延长线段 AB,所得的射线记作射线AB,如图(2);
02
知识精讲
B
A
a
图(1)
B
图(2)
A
②延长线段 BA(或反向延长线段 AB),所得的射线记作射线BA,如图(3);
B
图(3)
A
射线AB与射线BA是同一条射线吗?
02
知识精讲
B
A
B
A
【分析】不是,射线AB以A为端点,射线BA以B为端点。
注意:
表示射线时,端点字母一定写在左边
同时延长线段a的两端,所得的直线记作直线AB或直线BA,也可以记作直线l,如图(4)
02
知识精讲
2.如何由一条线段得到一条直线
B
A
l
图(4)
B
A
a
图(1)
图形 命名 不同点
直线 直线AB或直线BA或直线l 没有端点,可向两边无限延伸,不可测量
射线 射线AB(端点字母在左) 有一个端点A,可向一边无限延伸,不可测量
段 线 线段AB或线段BA或线段a 有两个端点A、B,不可延伸,可测量
直线VS射线VS线段
02
知识精讲
B
A
B
A
a
B
A
l
练一练——1.如图,已知点A、B、C。
(1)画线段AB;
(2)画射线BC;
(3)画直线AC。
02
知识精讲
B
C
A
解:(1)用直尺连接点A,B,线段AB即为所求;
(2)用直尺连接点B,C,并向BC方向延长,射线BC即为所求;
(3)用直尺连接点A,C,并向两端延长,直线AC即为所求。
2.根据下列语句,分别画出图形:
(1)直线l经过点A、B;
(2)点A在直线l外,点B在直线l上;
(3)直线a、b相交于点O;
(4)点P在直线a外,经过点P的直线b与直线a相交于点Q。
A
B
l
a
b
O
a
P
b
Q
02
知识精讲
l
A
B
3.如图,点B、C在线段AD上。
(1)图中以A为一个端点的线段有几条 是哪几条 以B为一个端点的线段呢
(2)图中以A、B、C、D四点中的两点为端点的线段有几条 是哪几条
解:(1)以A为一个端点的线段有线段AB、AC、AD,共3条;
02
知识精讲
以B为一个端点的线段有线段BA、BC、BD,共3条。
A
B
D
C
(2)线段AB、AC、AD、BC、BD、CD,共6条。
4.如图:
(1)有几条线段
(2)有几条射线 有几条射线可以用图中字母表示
(3)有几条直线
(4)一条直线上标出n个点,有几条线段 有几条射线
02
知识精讲
解:(1)6条(线段AB、AC、AD、BC、BD、CD);
(2)8条(A、B、C、D四个端点分别对应2条射线),
注意:
射线AD,即射线AC,即射线AB
A
B
D
C
6条(射线AD、射线BA、射线BD、射线CA、射线CD、射线DA);
4.如图:
(1)有几条线段
(2)有几条射线 有几条射线可以用图中字母表示
(3)有几条直线
(4)一条直线上标出n个点,有几条线段 有几条射线
02
知识精讲
A
B
D
C
(3)1条(直线AD);
注意:
直线AD,即直线AC,即直线AB,即直线BD,
即直线BC,即直线CD
(4)条,2n条。
活动——1.如图,从甲地到乙地有三条路,走哪条路较近
02
知识精讲
2.在上图中,从甲地到乙地能否修一条最短的路 如果能,你认为这条路应该怎样修
②
02
知识精讲
基本事实2、距离
通过实践,人们总结出如下基本事实:
两点之间的所有连线中,线段最短。
简单说成:两点之间,线段最短。
两点之间线段的长度叫作这两点之间的距离。
练一练——由火车站到汽车站,走下面哪条路线更近 为什么
(1)火车站→运河路→青年路→汽车站;
(2)火车站→运河路→世纪大道→解放路→汽车站。
解:(1)为黄色路线,
(2)为绿色路线,
∵两点之间线段最短;
∴(1)对应的红色路线更近。
02
知识精讲
例1、(1)要在墙上固定一根木条,至少需要两根钉子,理由是_________________;
(2)如图,点A、B在直线l上,点C是直线l外一点,可知CA+CB>AB,其依据是___________________。
03
典例精析
两点确定一条直线
两点之间,线段最短
知识精讲
例2、(1)若平面内有4个点,过其中任意两点画射线,最多可以画________条。
【分析】
设平面内这4个点分别为A,B,C,D,且任意3个点不共线,
过任意两点画射线,则有射线AB,射线BA,射线AC,射线CA,射线AD,射线DA,射线BC,射线CB,射线BD,射线DB,射线CD,射线DC,共12条。
12
03
典例精析
知识精讲
例2、(2)如图,棋盘上有黑、白两色棋子若干,若直线l经过3枚颜色相同的棋子,则这样的直线共有________条。
3
03
典例精析
知识精讲
两个基本事实:
1.两点确定一条直线。
2.两点之间,线段最短。
课后总结
6.1.1 直线、射线、线段——概念
汇报人:WPS
第6章 平面图形的初步认识
6.1.1 直线、射线、线段——概念
汇报人:WPS
教学目标
01
理解线段、射线和直线的联系与区别
02
掌握两个基本事实,理解两点之间的距离的概念
直线、射线、线段的概念
知识精讲
小学里,我们已经初步认识了直线、射线与线段。在下面的图片中,哪些图形可以看作是直线、射线、线段
01
射线
线段
直线
课堂引入
知识精讲
问题——将一根细木条固定到墙上,使其不能转动,至少需要几颗钉子
01
课堂引入
假如只钉一颗钉子,细木条可以绕着这颗钉子转动。
再打一颗钉子,这根细本条
就固定在墙上了。
如图,将细木条看作一条直线,一颗钉子看作一个点,过一点可以画无数条直线,过两点只能画一条直线。
01
课堂引入
知识精讲
02
知识精讲
基本事实1
通过实践,人们总结出如下基本事实:
两点确定一条直线。
如图1,我们可以用直线上的两点来表示这条直线,记作直线AB或直线BA,也可以记作直线l。
02
知识精讲
如图2(1),直线上的一点将直线分成两条射线;
B
A
l
图1
图2(1)
如图2(2),由直线上的两点可以得到一条线段。
图2(2)
直线
和直线的表示类似,图3(1)中的射线记作射线AB,其中点A是射线的端点。
02
知识精讲
图3(2)中的线段记作线段AB或线段BA,也可以记作线段a,其中点A,B是线段的端点。
B
A
图3(1)
B
A
图3(2)
a
射线、线段
讨论——1.如何由一条线段得到一条射线
①延长线段 AB,所得的射线记作射线AB,如图(2);
02
知识精讲
B
A
a
图(1)
B
图(2)
A
②延长线段 BA(或反向延长线段 AB),所得的射线记作射线BA,如图(3);
B
图(3)
A
射线AB与射线BA是同一条射线吗?
02
知识精讲
B
A
B
A
【分析】不是,射线AB以A为端点,射线BA以B为端点。
注意:
表示射线时,端点字母一定写在左边
同时延长线段a的两端,所得的直线记作直线AB或直线BA,也可以记作直线l,如图(4)
02
知识精讲
2.如何由一条线段得到一条直线
B
A
l
图(4)
B
A
a
图(1)
图形 命名 不同点
直线 直线AB或直线BA或直线l 没有端点,可向两边无限延伸,不可测量
射线 射线AB(端点字母在左) 有一个端点A,可向一边无限延伸,不可测量
段 线 线段AB或线段BA或线段a 有两个端点A、B,不可延伸,可测量
直线VS射线VS线段
02
知识精讲
B
A
B
A
a
B
A
l
练一练——1.如图,已知点A、B、C。
(1)画线段AB;
(2)画射线BC;
(3)画直线AC。
02
知识精讲
B
C
A
解:(1)用直尺连接点A,B,线段AB即为所求;
(2)用直尺连接点B,C,并向BC方向延长,射线BC即为所求;
(3)用直尺连接点A,C,并向两端延长,直线AC即为所求。
2.根据下列语句,分别画出图形:
(1)直线l经过点A、B;
(2)点A在直线l外,点B在直线l上;
(3)直线a、b相交于点O;
(4)点P在直线a外,经过点P的直线b与直线a相交于点Q。
A
B
l
a
b
O
a
P
b
Q
02
知识精讲
l
A
B
3.如图,点B、C在线段AD上。
(1)图中以A为一个端点的线段有几条 是哪几条 以B为一个端点的线段呢
(2)图中以A、B、C、D四点中的两点为端点的线段有几条 是哪几条
解:(1)以A为一个端点的线段有线段AB、AC、AD,共3条;
02
知识精讲
以B为一个端点的线段有线段BA、BC、BD,共3条。
A
B
D
C
(2)线段AB、AC、AD、BC、BD、CD,共6条。
4.如图:
(1)有几条线段
(2)有几条射线 有几条射线可以用图中字母表示
(3)有几条直线
(4)一条直线上标出n个点,有几条线段 有几条射线
02
知识精讲
解:(1)6条(线段AB、AC、AD、BC、BD、CD);
(2)8条(A、B、C、D四个端点分别对应2条射线),
注意:
射线AD,即射线AC,即射线AB
A
B
D
C
6条(射线AD、射线BA、射线BD、射线CA、射线CD、射线DA);
4.如图:
(1)有几条线段
(2)有几条射线 有几条射线可以用图中字母表示
(3)有几条直线
(4)一条直线上标出n个点,有几条线段 有几条射线
02
知识精讲
A
B
D
C
(3)1条(直线AD);
注意:
直线AD,即直线AC,即直线AB,即直线BD,
即直线BC,即直线CD
(4)条,2n条。
活动——1.如图,从甲地到乙地有三条路,走哪条路较近
02
知识精讲
2.在上图中,从甲地到乙地能否修一条最短的路 如果能,你认为这条路应该怎样修
②
02
知识精讲
基本事实2、距离
通过实践,人们总结出如下基本事实:
两点之间的所有连线中,线段最短。
简单说成:两点之间,线段最短。
两点之间线段的长度叫作这两点之间的距离。
练一练——由火车站到汽车站,走下面哪条路线更近 为什么
(1)火车站→运河路→青年路→汽车站;
(2)火车站→运河路→世纪大道→解放路→汽车站。
解:(1)为黄色路线,
(2)为绿色路线,
∵两点之间线段最短;
∴(1)对应的红色路线更近。
02
知识精讲
例1、(1)要在墙上固定一根木条,至少需要两根钉子,理由是_________________;
(2)如图,点A、B在直线l上,点C是直线l外一点,可知CA+CB>AB,其依据是___________________。
03
典例精析
两点确定一条直线
两点之间,线段最短
知识精讲
例2、(1)若平面内有4个点,过其中任意两点画射线,最多可以画________条。
【分析】
设平面内这4个点分别为A,B,C,D,且任意3个点不共线,
过任意两点画射线,则有射线AB,射线BA,射线AC,射线CA,射线AD,射线DA,射线BC,射线CB,射线BD,射线DB,射线CD,射线DC,共12条。
12
03
典例精析
知识精讲
例2、(2)如图,棋盘上有黑、白两色棋子若干,若直线l经过3枚颜色相同的棋子,则这样的直线共有________条。
3
03
典例精析
知识精讲
两个基本事实:
1.两点确定一条直线。
2.两点之间,线段最短。
课后总结
6.1.1 直线、射线、线段——概念
汇报人:WPS
同课章节目录
