6.1图形的认识 课件(共39张PPT)
文档属性
| 名称 | 6.1图形的认识 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 74.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-24 15:01:40 | ||
图片预览









文档简介
(共39张PPT)
第6章 基本的几何图形
6.1 图形的认识
学习目标
1. 能识别生活中的基本几何体,并会给它们分类;
3. 了解点动成线、线动成面、面动成体,感受点、线、面、体之间的关系,理解点是构成图形的基本元素。
2. 知道几何图形是由点、线、面组成的,会区分平面图形和立体图形;
观察与发现
图1是常见的生活物品,我们只研究它们的形状,可以得到图2中的图形。
长方体
正方体
圆锥
球
圆柱
概括与表达
长方体、正方体、球、圆柱、圆锥等都是几何体,又简称为体。
几何体是由面围成的。
例如,长方体由六个平的面围成,球由一个曲的面围成,圆柱由两个平的底面和一个曲的侧面围成。
观察与发现
生活中,操场的地面、平静的水面、镜面、黑板面等都给我们以平面的形象。数学中的平面是从实物中抽象出来的,没有厚薄,没有边界,向四面八方无限延展。除平面外,我们还会经常见到弯曲的面的形象 (如图)。
思考与交流
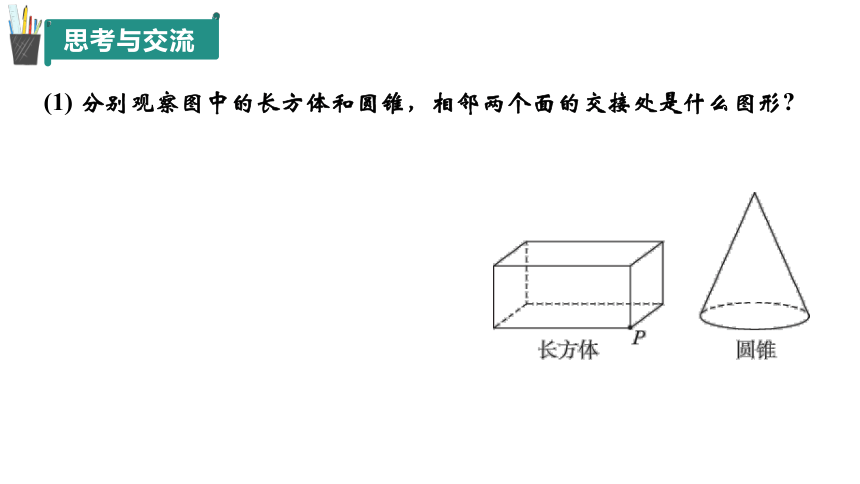
(1) 分别观察图中的长方体和圆锥,相邻两个面的交接处是什么图形
思考与交流
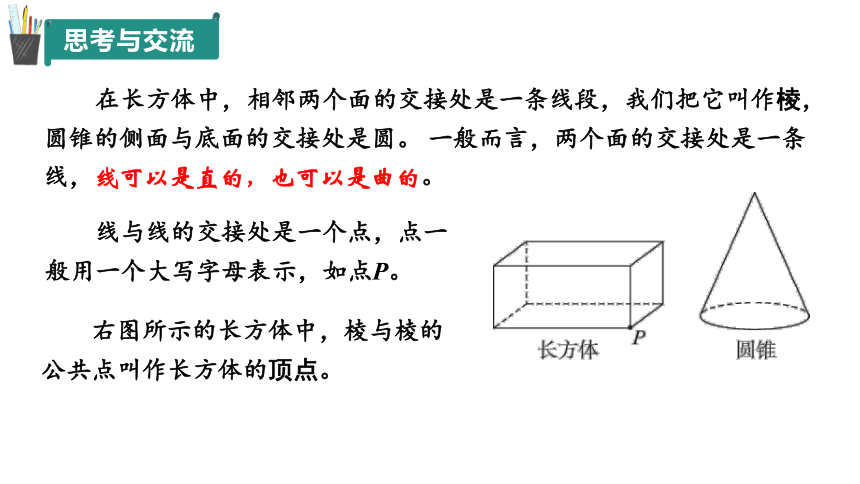
在长方体中,相邻两个面的交接处是一条线段,我们把它叫作棱,圆锥的侧面与底面的交接处是圆。 一般而言,两个面的交接处是一条线,线可以是直的,也可以是曲的。
右图所示的长方体中,棱与棱的公共点叫作长方体的顶点。
线与线的交接处是一个点,点一般用一个大写字母表示,如点P。
思考与交流
(2) 长方体、圆柱、圆锥、球上的点是否在同一个平面内
三角形、平行四边形、圆上的点是否在同一个平面内
长方体、圆柱、圆锥、球上的点不都在同一个平面内。相反,三角形、平行四边形、圆上的点都在同一个平面内。
概括与表达
如果几何图形上的点不都在同一个平面内,那么这样的几何图形叫作立体图形。
如果几何图形上的点都在同一个平面内,那么这样的几何图形叫作平面图形。
长方体、圆柱、圆锥、球等都是立体图形。
线段、角、三角形、平行四边形、梯形、圆等都是平面图形。
几何图形可分为立体图形和平面图形两类。
思考与交流
如图,流星给我们以 “点动成线”的形象,折扇扇骨移动形成的扇面给我们以 “线动成面”的形象,旋转门给我们以 “面动成体”的形象。点、线、面、体的运动变化,能组成各种各样的几何图形。点是构成图形的基本元素。
归纳与总结
点动成——
线动成——
面动成——
线
面
体
线与线相交成点
面与面相交成线
体是由面组成
点,线,面,体关系
动态
静态
归纳与总结
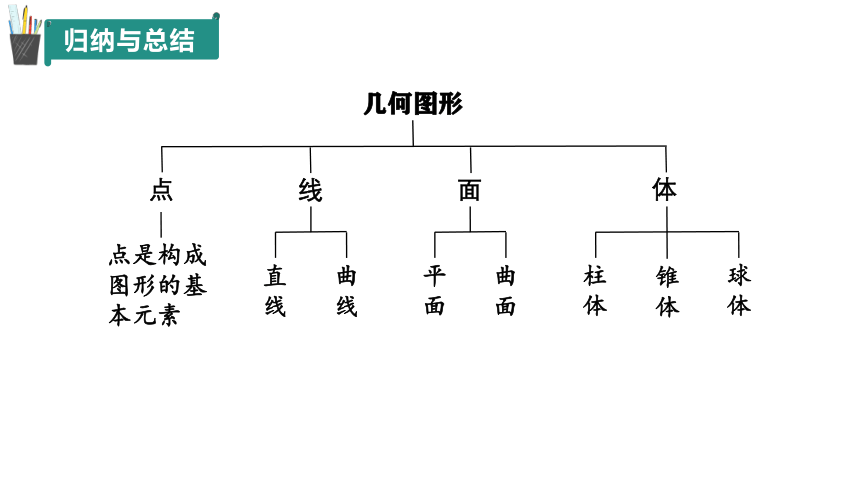
几何图形
点
线
面
体
点是构成图形的基本元素
直线
曲线
平面
曲面
柱体
球体
锥体
新知巩固
1.观察下列实物图片,描述图中物体的主要形状。
粮囤
水立方
储气罐
长方体
球
圆锥
圆柱
新知巩固
2.把几何图形圆、圆柱、球、扇形、三角形、长方体、正方体、直角分别填到下面的大括号里(用顿号隔开):
立体图形:{ …};
平面图形:{ …}。
圆柱、球、长方体、正方体
圆、扇形、三角形、直角
新知巩固
3.将下列平面图形分别绕图中的虚线(轴线)旋转一周,可以得到什么立体图形
新知巩固
4.举出生活中 “点动成线”“线动成面”“面动成体”的例子。
点动成线:夜晚的流星划过天空时留下一道明亮的光线;
线动成面:钟表上的分针转动一周形成一个圆面;
面动成体:一枚硬币在光滑的桌面上快速旋转形成球。
拓展与延伸
1.摆一摆,看一看,回答下列问题:
(1)用3根小木棍首尾相接组成的图形是平面图形还是立体图形
(2)用6根小木棍首尾相接组成的图形是平面图形还是立体图形
答:(1)用3根小木棍首尾相接组成的图形是平面图形。
(2)用6根小木棍首尾相接组成的图形可能是平面图形也可能是立体图形。
拓展与延伸
2.观察下列几种多面体模型,并完成下表:
四面体 长方体 正八面体 正十二面体
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4
长方体 6 12
正八面体 6 12
正十二面体 20 30
6
8
8
12
V+F-E=2
1.几何图形是由点、线、面组成的,会区分平面图形和立体图形。
2.点动成线、线动成面、面动成体,感受点、线、面、体之间的关系。
课堂检测
基础过关
1.下列说法不正确的是( )
A.正方体有六个面,这六个面都是平的
B.圆柱有三个面,这三个面都是平的
C.圆锥有两个面,这两个面中一个是平的,一个是曲的
D.球由一个面围成,这个面是曲的
B
课堂检测
基础过关
2.下列生活形象解释正确的一项是( )
A.旋转一扇门,门在空中运动的轨迹:点动成线
B.天空划过的流星:线动成面
C.汽车雨刷在挡风玻璃上划过的痕迹:线动成面
D.将一张纸折叠后,纸上会出现一条线:面动成体
C
课堂检测
基础过关
3.异形手提盒包装设计因其结构造型独特,具有丰富的艺术性和实用性.将如图所示的手提盒主体的形状抽象成几何体正确的是( )
D
A. B. C. D.
4.如图,是位于江西遂川县左安镇桃源村,曾被推介为世界十大最美梯田的桃园梯田,最上层的称为“望天丘”,其直观图形形状近似可看作( )
A.三角形 B.五边形
C.菱形 D.矩形
课堂检测
能力提升
D
课堂检测
基础过关
5.下列各组图形都是平面图形的一组是( )
A.线段、圆、圆锥、球
B.角、三角形、长方形、圆柱
C.长方体、圆柱、棱锥、球
D.圆、三角形、正方形、长方形
D
课堂检测
基础过关
6.下列几何体中与其余三个不属于同一类几何体的是( )
C
A. B. C. D.
课堂检测
基础过关
7.下面几种几何图形中,属于立体图形的是_______。
①三角形 ②长方形 ③正方体 ④圆 ⑤圆柱
③⑤
8.用一个平面去截下列几何体,截面可能是三角形的是________(填序号)。
①长方体;②正方体;③圆柱;④圆锥
①②④
课堂检测
基础过关
9.如图,将长和宽分别为和的长方形分别绕它的长和宽旋转一周,算一算,得到的两个几何体的体积相等吗 如果不相等,哪个体积大 (π取3)
解:将长方形分别绕它的长和宽旋转一周,得到都是圆柱体,将长和宽分别为10cm和6cm的长方形绕它的长旋转一周,得到圆柱底面半径6cm,高10cm,则体积为10×π62=360π=360×3=1080(cm3),
将长和宽分别为10cm和6cm的长方形绕它的宽旋转一周,得到圆柱底面半径10cm,高6cm,则体积为6×π102=600π=600×3=1800(cm3),
所以得到的两个几何体的体积不相等,绕它的宽旋转一周得到几何体的体积更大。
1.下列物体从左到右可近似地看成( )
课堂检测
能力提升
A.球、正方体、圆柱、圆锥 B.球、长方体、棱柱、圆锥
C.球、正方体、棱柱、棱锥 D.圆柱、正方体、圆柱、棱锥
A
课堂检测
能力提升
2.如图,由所给的平面图形绕虚线旋转一周,可得到的几何体是( )
D
A. B. C. D.
课堂检测
能力提升
3.如图是一种折叠灯笼,压扁的时候,它看起来是平面的,提起来却变成了美丽的圆柱形灯笼。这个过程中蕴含的数学原理是 。
面动成体
课堂检测
能力提升
4.下列说法:
①三棱锥的底面是三角形;
②棱柱有个面,个顶点,条棱;
③若直棱柱的底面边长都相等,则它的各个侧面的面积也相等;
④圆锥有两个面,底面与侧面相交形成曲线;
⑤时钟的秒针旋转时,形成一个圆面,这说明了点动成线;
⑥如果用一个平面去截八棱柱,截面形状一定不是九边形.
其中正确的有 。
4个
课堂检测
能力提升
5.如图是8个立体图形。
③④⑧
其中,是柱体的有 ,是锥体的有 ,有曲面的有 。(填序号)
①②⑤⑦⑧
④⑥
课堂检测
能力提升
(1)
B
6.指出图中几何体截面形状的标号______。
课堂检测
能力提升
6.指出图中几何体截面形状的标号______。
C
(2)
课堂检测
能力提升
7.小明学习了“面动成体”之后,他用一个边长分别为,和的直角三角形,绕不同的边所在的直线旋转一周,得到了如图所示的几何体。
(1) 绕的边所在的直线旋转一周,可以得到图_____;绕的边所在的直线旋转一周,可以得到图______;绕的边所在的直线旋转一周,可以得到图______;(请填写序号)
①
②
③
课堂检测
能力提升
(2)请计算图①和图②中几何体的体积。(结果保留,圆锥体积×底面积×高)
解:(2)图①中几何体的体积为:
;
图②中几何体的体积为:
。
7.小明学习了“面动成体”之后,他用一个边长分别为,和的直角三角形,绕不同的边所在的直线旋转一周,得到了如图所示的几何体。
课堂检测
能力提升
8.欧拉(,1707年1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数、棱数、面数之间存在一定的数量关系,给出了著名的欧拉公式。
(1)观察下列多面体,并把下表补充完整:
名称 三棱锥 三棱柱 正方体 正八面体
图形
顶点数 4 ______ ______ ______
棱数 6 ______ ______ ______
面数 4 ______ ______ ______
6
9
5
8
12
6
6
12
8
课堂检测
能力提升
(2)分析表中的数据,请写出、、之间的等量关系为:______;一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是______;
(2)解:分析表中的数据,能发现、、之间的关系为:,
,,,
,
,
故答案为:,20;
课堂检测
能力提升
(3)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱.请问该多面体表面三角形与八边形的个数之和是多少?
(3)解:依题意,设该多面体表面三角形的个数为个,八边形的个数为个,
有48个顶点,每个顶点处都有3条棱,
共有(条,
,解得。
。
∴该多面体表面三角形与八边形的个数之和是。
第6章 基本的几何图形
6.1 图形的认识
学习目标
1. 能识别生活中的基本几何体,并会给它们分类;
3. 了解点动成线、线动成面、面动成体,感受点、线、面、体之间的关系,理解点是构成图形的基本元素。
2. 知道几何图形是由点、线、面组成的,会区分平面图形和立体图形;
观察与发现
图1是常见的生活物品,我们只研究它们的形状,可以得到图2中的图形。
长方体
正方体
圆锥
球
圆柱
概括与表达
长方体、正方体、球、圆柱、圆锥等都是几何体,又简称为体。
几何体是由面围成的。
例如,长方体由六个平的面围成,球由一个曲的面围成,圆柱由两个平的底面和一个曲的侧面围成。
观察与发现
生活中,操场的地面、平静的水面、镜面、黑板面等都给我们以平面的形象。数学中的平面是从实物中抽象出来的,没有厚薄,没有边界,向四面八方无限延展。除平面外,我们还会经常见到弯曲的面的形象 (如图)。
思考与交流
(1) 分别观察图中的长方体和圆锥,相邻两个面的交接处是什么图形
思考与交流
在长方体中,相邻两个面的交接处是一条线段,我们把它叫作棱,圆锥的侧面与底面的交接处是圆。 一般而言,两个面的交接处是一条线,线可以是直的,也可以是曲的。
右图所示的长方体中,棱与棱的公共点叫作长方体的顶点。
线与线的交接处是一个点,点一般用一个大写字母表示,如点P。
思考与交流
(2) 长方体、圆柱、圆锥、球上的点是否在同一个平面内
三角形、平行四边形、圆上的点是否在同一个平面内
长方体、圆柱、圆锥、球上的点不都在同一个平面内。相反,三角形、平行四边形、圆上的点都在同一个平面内。
概括与表达
如果几何图形上的点不都在同一个平面内,那么这样的几何图形叫作立体图形。
如果几何图形上的点都在同一个平面内,那么这样的几何图形叫作平面图形。
长方体、圆柱、圆锥、球等都是立体图形。
线段、角、三角形、平行四边形、梯形、圆等都是平面图形。
几何图形可分为立体图形和平面图形两类。
思考与交流
如图,流星给我们以 “点动成线”的形象,折扇扇骨移动形成的扇面给我们以 “线动成面”的形象,旋转门给我们以 “面动成体”的形象。点、线、面、体的运动变化,能组成各种各样的几何图形。点是构成图形的基本元素。
归纳与总结
点动成——
线动成——
面动成——
线
面
体
线与线相交成点
面与面相交成线
体是由面组成
点,线,面,体关系
动态
静态
归纳与总结
几何图形
点
线
面
体
点是构成图形的基本元素
直线
曲线
平面
曲面
柱体
球体
锥体
新知巩固
1.观察下列实物图片,描述图中物体的主要形状。
粮囤
水立方
储气罐
长方体
球
圆锥
圆柱
新知巩固
2.把几何图形圆、圆柱、球、扇形、三角形、长方体、正方体、直角分别填到下面的大括号里(用顿号隔开):
立体图形:{ …};
平面图形:{ …}。
圆柱、球、长方体、正方体
圆、扇形、三角形、直角
新知巩固
3.将下列平面图形分别绕图中的虚线(轴线)旋转一周,可以得到什么立体图形
新知巩固
4.举出生活中 “点动成线”“线动成面”“面动成体”的例子。
点动成线:夜晚的流星划过天空时留下一道明亮的光线;
线动成面:钟表上的分针转动一周形成一个圆面;
面动成体:一枚硬币在光滑的桌面上快速旋转形成球。
拓展与延伸
1.摆一摆,看一看,回答下列问题:
(1)用3根小木棍首尾相接组成的图形是平面图形还是立体图形
(2)用6根小木棍首尾相接组成的图形是平面图形还是立体图形
答:(1)用3根小木棍首尾相接组成的图形是平面图形。
(2)用6根小木棍首尾相接组成的图形可能是平面图形也可能是立体图形。
拓展与延伸
2.观察下列几种多面体模型,并完成下表:
四面体 长方体 正八面体 正十二面体
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4
长方体 6 12
正八面体 6 12
正十二面体 20 30
6
8
8
12
V+F-E=2
1.几何图形是由点、线、面组成的,会区分平面图形和立体图形。
2.点动成线、线动成面、面动成体,感受点、线、面、体之间的关系。
课堂检测
基础过关
1.下列说法不正确的是( )
A.正方体有六个面,这六个面都是平的
B.圆柱有三个面,这三个面都是平的
C.圆锥有两个面,这两个面中一个是平的,一个是曲的
D.球由一个面围成,这个面是曲的
B
课堂检测
基础过关
2.下列生活形象解释正确的一项是( )
A.旋转一扇门,门在空中运动的轨迹:点动成线
B.天空划过的流星:线动成面
C.汽车雨刷在挡风玻璃上划过的痕迹:线动成面
D.将一张纸折叠后,纸上会出现一条线:面动成体
C
课堂检测
基础过关
3.异形手提盒包装设计因其结构造型独特,具有丰富的艺术性和实用性.将如图所示的手提盒主体的形状抽象成几何体正确的是( )
D
A. B. C. D.
4.如图,是位于江西遂川县左安镇桃源村,曾被推介为世界十大最美梯田的桃园梯田,最上层的称为“望天丘”,其直观图形形状近似可看作( )
A.三角形 B.五边形
C.菱形 D.矩形
课堂检测
能力提升
D
课堂检测
基础过关
5.下列各组图形都是平面图形的一组是( )
A.线段、圆、圆锥、球
B.角、三角形、长方形、圆柱
C.长方体、圆柱、棱锥、球
D.圆、三角形、正方形、长方形
D
课堂检测
基础过关
6.下列几何体中与其余三个不属于同一类几何体的是( )
C
A. B. C. D.
课堂检测
基础过关
7.下面几种几何图形中,属于立体图形的是_______。
①三角形 ②长方形 ③正方体 ④圆 ⑤圆柱
③⑤
8.用一个平面去截下列几何体,截面可能是三角形的是________(填序号)。
①长方体;②正方体;③圆柱;④圆锥
①②④
课堂检测
基础过关
9.如图,将长和宽分别为和的长方形分别绕它的长和宽旋转一周,算一算,得到的两个几何体的体积相等吗 如果不相等,哪个体积大 (π取3)
解:将长方形分别绕它的长和宽旋转一周,得到都是圆柱体,将长和宽分别为10cm和6cm的长方形绕它的长旋转一周,得到圆柱底面半径6cm,高10cm,则体积为10×π62=360π=360×3=1080(cm3),
将长和宽分别为10cm和6cm的长方形绕它的宽旋转一周,得到圆柱底面半径10cm,高6cm,则体积为6×π102=600π=600×3=1800(cm3),
所以得到的两个几何体的体积不相等,绕它的宽旋转一周得到几何体的体积更大。
1.下列物体从左到右可近似地看成( )
课堂检测
能力提升
A.球、正方体、圆柱、圆锥 B.球、长方体、棱柱、圆锥
C.球、正方体、棱柱、棱锥 D.圆柱、正方体、圆柱、棱锥
A
课堂检测
能力提升
2.如图,由所给的平面图形绕虚线旋转一周,可得到的几何体是( )
D
A. B. C. D.
课堂检测
能力提升
3.如图是一种折叠灯笼,压扁的时候,它看起来是平面的,提起来却变成了美丽的圆柱形灯笼。这个过程中蕴含的数学原理是 。
面动成体
课堂检测
能力提升
4.下列说法:
①三棱锥的底面是三角形;
②棱柱有个面,个顶点,条棱;
③若直棱柱的底面边长都相等,则它的各个侧面的面积也相等;
④圆锥有两个面,底面与侧面相交形成曲线;
⑤时钟的秒针旋转时,形成一个圆面,这说明了点动成线;
⑥如果用一个平面去截八棱柱,截面形状一定不是九边形.
其中正确的有 。
4个
课堂检测
能力提升
5.如图是8个立体图形。
③④⑧
其中,是柱体的有 ,是锥体的有 ,有曲面的有 。(填序号)
①②⑤⑦⑧
④⑥
课堂检测
能力提升
(1)
B
6.指出图中几何体截面形状的标号______。
课堂检测
能力提升
6.指出图中几何体截面形状的标号______。
C
(2)
课堂检测
能力提升
7.小明学习了“面动成体”之后,他用一个边长分别为,和的直角三角形,绕不同的边所在的直线旋转一周,得到了如图所示的几何体。
(1) 绕的边所在的直线旋转一周,可以得到图_____;绕的边所在的直线旋转一周,可以得到图______;绕的边所在的直线旋转一周,可以得到图______;(请填写序号)
①
②
③
课堂检测
能力提升
(2)请计算图①和图②中几何体的体积。(结果保留,圆锥体积×底面积×高)
解:(2)图①中几何体的体积为:
;
图②中几何体的体积为:
。
7.小明学习了“面动成体”之后,他用一个边长分别为,和的直角三角形,绕不同的边所在的直线旋转一周,得到了如图所示的几何体。
课堂检测
能力提升
8.欧拉(,1707年1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数、棱数、面数之间存在一定的数量关系,给出了著名的欧拉公式。
(1)观察下列多面体,并把下表补充完整:
名称 三棱锥 三棱柱 正方体 正八面体
图形
顶点数 4 ______ ______ ______
棱数 6 ______ ______ ______
面数 4 ______ ______ ______
6
9
5
8
12
6
6
12
8
课堂检测
能力提升
(2)分析表中的数据,请写出、、之间的等量关系为:______;一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是______;
(2)解:分析表中的数据,能发现、、之间的关系为:,
,,,
,
,
故答案为:,20;
课堂检测
能力提升
(3)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱.请问该多面体表面三角形与八边形的个数之和是多少?
(3)解:依题意,设该多面体表面三角形的个数为个,八边形的个数为个,
有48个顶点,每个顶点处都有3条棱,
共有(条,
,解得。
。
∴该多面体表面三角形与八边形的个数之和是。
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
